Schulz und die Kanzlerfrage: Inferenzstatistik im Datenjournalismus
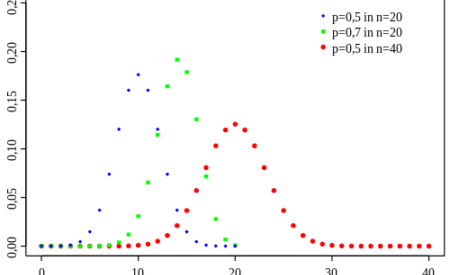
Die Wahlkampfzeit ist auch die Zeit der Daten und ihrer Visualisierung in den Medien. Diese Visualisierung soll beim wahlberechtigten Bürger das Verständnis für Zusammenhänge fördern, hat aber öfters den negativen Nebeneffekt, dass sie den Eindruck erweckt, dass die Interpretation dieser Daten kinderleicht ist. Wer sich im Studium mit Inferenzstatistik befassen musste, weiß es besser. Inferenzstatistik trifft Wahrscheinlichkeitsaussagen über eine Grundgesamtheit. Wir haben dabei Daten aus einer Stichprobe vorliegen, möchten anhand dieser jedoch Aussagen über die Grundgesamtheit treffen. Um diese Aussagen machen zu können, muss der Studierende die Annahmen und Bedingungen kennen, die erfüllt werden müssen, damit bestimmte statistische Verfahren angewandt werden können.
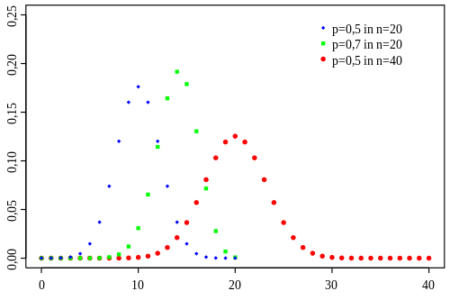
Wahlkampfstatistik ist Inferenzstatistik, die anhand von Stichproben Aussagen über die Grundgesamtheit der Wahlberechtigten macht. Eine der wichtigsten Aussagen ist die über den künftigen Kanzler/die künftige Kanzlerin.
SPD-Kanzlerkandidat Martin Schulz hat einen beispiellosen Absturz in der Wählergunst hinter sich: Im Februar erreichte er in der Kanzlerfrage1 des Instituts Infratest dimap mit 50 % einen Höchstwert und lag 16 Punkte vor Kanzlerin Angela Merkel (34 %). Ende August ist der Wert von Schulz auf 26 % abgesunken (Merkel 49 %). Das ist eine statistisch signifikante Veränderung, die so groß ist, das auch ein Laie sie ohne ein besonderes mathematisches Verfahren feststellen kann. Der Datenjournalist aber muss sich generell fragen, ab wann eine Änderung statistisch signifikant ist und welches Signifikanzniveau sinnvoll ist.
Kann er z. B. mit 95 % (das bedeutet eine Irrtumswahrscheinlichkeit von 5 %) annehmen, dass sich der Umfragewert von Schulz vom Februar 2017 geändert hat?
Diese Frage lässt sich mittels Inferenzstatistik in acht Schritten beantworten.
1. Erwartungswert festlegen: p0 = 50 % (500 Befragte im Februar 2017)
2. Hypothesenformulierung
Nullhypothese H0: Der Umfragewert für Schulz beträgt unverändert 50 %. (p0 = 50 % = 0,50)
Alternativhypothese H1: Der Umfragewert hat sich verändert. p1≠ 0,50
3. Zahl der Befragten (Stichprobenumfang) bestimmen: n = 10002
4. Irrtumswahrscheinlichkeit festlegen: α= 5 % = 0,05
5. X bestimmen: Zahl der Personen in der Stichprobe vom Umfang 1000, welche Schulz als Kanzler wählen würden.
6. Annahmen festlegen: X ist binomialverteilt mit p = 0,50 (falls die Nullhypothese richtig ist).
7. Zweiseitigen Signifikanztest durchführen:
Bei diesem Signifikanztest kann eine Abweichung vom Erwartungswert p0 in beide Richtungen erfolgen. Abweichungen vom Erwartungswert nach rechts oder links haben bei einer Binomialverteilung die gleiche Wahrscheinlichkeit.
Wird ein zweiseitiger Signifikanztest durchgeführt, so ist die vorgegebene Irrtumswahrscheinlichkeit zu halbieren, um auf beiden Seiten des Erwartungswerts einen Ablehnungsbereich mit derselben Irrtumswahrscheinlichkeit festlegen zu können. Dabei ist bl die größte Zahl des Ablehnungsbereichs bei einer Unterschreitung des Erwartungswerts und br die kleinste Zahl des Ablehnungsbereichs bei einer Überschreitung des Erwartungswerts.
a) Die linke Grenze – nicht weniger als bl Wähler dürfen für Schulz stimmen um die Nullhypothese beizubehalten.
5 % : 2 = 2,5 % = 0,025
p(X ≤ bl) ≤ 0,025
Aus der Tabelle der kumulierten Binomialverteilung kann entnommen werden (n = 1000, p = 0,50).
Für X = 468; p(X ≤ 468) = 0,0231
Folglich ist 468 (46,8 %) die größte Zahl des Ablehnungsbereichs (bl).
b) Die rechte Grenze – nicht mehr als br Wähler dürfen für Schulz stimmen um die Nullhypothese beizubehalten.
p(X ≥ br) ≤ 0,025
p(X ≤ br -1) ≥ 0,975
Aus der Tabelle der kumulierten Binomialverteilung kann entnommen werden (n = 1000, p = 0,50).
Für X = 531; p(X ≤ 531) = 0,9769
Folglich ist 531 (53,1 %) die kleinste Zahl des Ablehnungsbereichs (br)
8. Entscheidungsregel bestimmen
Als Entscheidungsregel ergibt sich, dass die Nullhypothese genau dann beibehalten wird, wenn X im Bereich [bl;br] liegt. Damit ist die Entscheidungsregel: Für 468<X<531 = 46,8 %<X<53,1 %
Bezogen auf den Umfragewert von Schulz von Februar 2017 wird bei der Kanzlerfrage die Nullhypothese abgelehnt, wenn die nachfolgenden Umfragewerte unter 46,8 % oder über 53,1 % liegen (unter den Annahmen und Bedingungen unseres Testverfahrens).
Fußnoten
1. Frage: Wenn man den Bundeskanzler direkt wählen könnte: für wen würden Sie sich entscheiden, für Angela Merkel oder Martin Schulz?
Grundgesamtheit: Wahlberechtigte Bevölkerung in Deutschland ab 18 Jahren, Angaben in Prozent
Stichprobe: Repräsentative Zufallsauswahl/ Dual Frame
(Relation Festnetz-/Mobilfunknummern 70:30)
Erhebungsverfahren: Computergestützte Telefoninterviews (CATI)
Fallzahl: 1006 Befragte
Erhebungszeitraum: 30. bis 31. Januar 2017
Durchführendes Institut: Infratest dimap
2. Zur Vereinfachung habe ich mit einem Stichprobenumfang von 1000 gerechnet.


Es stellt sich nur eine Frage:
Hält die SPD die Masse für so blöd, oder sind die einfach nur so / zu blöd??
Wenn diese “demokratischen” Wahlen etwas in Richtung zweifelsfrei-eindeutiger Wahrheit verändern würden, wären sie schnell verboten – Das leichtfertige Kreuzchen auf dem Blankoscheck, für diesen multischizophrenen Parlamentarismus in Lobby-Marionettentheater, ist eine Schande für unsere Vernunftbegabung!
Nichtwählen ist hochmoralisch / ist unkorrumpierte MENSCHENWÜRDE!
Joe Dramiga schrieb (30. August 2017):
> […] Inferenzstatistik in acht Schritten
> […] 2. Hypothesenformulierung Nullhypothese […]: Der Umfragewert für Schulz beträgt unverändert 50 %.
> 8. Entscheidungsregel bestimmen […] Bezogen auf den Umfragewert von Schulz von Februar 2017 wird […] die Nullhypothese abgelehnt, wenn die nachfolgenden Umfragewerte unter 46,8 % oder über 53,1 % liegen
Falls der (bzw. jeder) nachfolgende Umfragewert unter 46,8 % oder über 53,1 % ermittelt wird, dann wäre die Hypothese offensichtlich falsch und zurückzuweisen, dass der (bzw. jeder) nachfolgende Umfragewert unverändert exakt 50 %;
und falls der (bzw. jeder) nachfolgende Umfragewert von exakt 50 % gefunden würde, dann wäre die entsprechende Hypothese offensichtlich bestätigt.
So weit, so schön.
Aber was gilt in den verbleibenden Fällen?
Falls z.B. ein (bzw. jeder) nachfolgende Umfragewert von exakt 48 % ermittelt würde — wohlgemerkt unter genau den Annahmen und Bedingungen des beschriebenen Testverfahrens, sofern es nachvollziehbar ist — ist die Hypothese, dass der (bzw. jeder) nachfolgende Umfragewert bei unverändert exakt 50 % liegt (also genau die im “Schritt 2” formulierte Nullhypothese) etwa bestätigt??
Mir scheint eher, dass dem selben Wort “Umfragewert” verschiedene Begriffs-Bedeutungen in den zitierten “Schritten” zuzuschreiben sind. …
p.s.
SciLogs-Kommentar-HTML-Test:
“H>sub<0>/sub<” wird dargestellt als: “H0”.
p.p.s.
SciLogs-Kommentar-LaTeX-Test:
“\( H_0 \) ” wird dargestellt als “\( H_0 \)”.
Nachtrag:
Die SciLogs-Kommentarvorschau (die nun dankenswerter Weise zumindest im Prinzip zur Verfügung gestellt ist, und die ich schon ein paar mal erfolgreich benutzt habe) schien gerade nicht mehr zu funktionieren. Deshalb hatte ich meinen vorausgehenden Kommentar eingereicht, ohne von einer solchen Kommentarvorschau profitieren zu können, und möchte den Fehler, den ich deshalb zunächst übersehen hatte, hiermit korrigieren:
“H<sub>0</sub>” wird dargestellt als: “H0”.
Soviel ich weiß, kann man die Nullhypothese nicht bestätigen oder beweisen. Bei einer Nicht-Ablehnung der Nullhypothese wird diese streng genommen weder unterstützt, noch wird die Gegenhypothese unterstützt. Ich denke es macht auch keinen Sinn von “exakt” zu reden, wenn wir eine Irrtumswahrscheinlichkeit von 5 % voraussetzen. Unter dieser Voraussetzung würde ich bei einem Wert von 48 % davon ausgehen, dass sich der Umfragewert nicht geändert hat und die Nullhypothese beibehalten.
Man könnte jetzt auf den Fehler 2. Art schauen. Der Fehler 2. Art ist die Wahrscheinlichkeit dafür, dass ein Umfragewert in den Annahmebereich der Nullhypothese fällt, obwohl die Alternativhypothese gilt.
Joe Dramiga schrieb (1. September 2017 @ 00:14):
> Ich denke es macht auch keinen Sinn von “exakt” zu reden, wenn wir eine Irrtumswahrscheinlichkeit von 5 % voraussetzen. Unter dieser Voraussetzung würde ich bei einem Wert von 48 % davon ausgehen, dass sich der Umfragewert nicht geändert hat
Ich denke bzw. unterstelle, dass die Gesamtanzahl befragter Personen in jeder Umfrage (d.h. im obigen Beitrag “Stichprobenumfang n = 1000“) sowie die tatsächlichen bzw. in Betracht gezogenen Anzahlen derjenigen Befragten in jeweils einer Umfrage, die “für Schulz stimmenwürden” (d.h. Zahlen wie z.B. 500 oder 468 oder 531 aus dem obigen Beitrag, oder 480 entsprechend dem Beispiel in meinem vorausgehenden Kommentar),
doch jeweils exakte natürliche Zahlen sind;
und dass die entsprechenden Prozentangaben des jeweiligen “Umfragewerts” einschließlich der ersten Dezimalstelle exakt und signifikant sind.
Demnach finde ich die Personenanzahl 480 ungleich zu 500, und den Umfragewert 48 % verändert gegenüber 50 %.
Aber:
wenn wir “eine Irrtumswahrscheinlichkeit von 5 % voraussetzen” und im oben gezeigten “Schritt 7.” berücksichtigen sollen,
dann bezieht sich solcher (möglicher) Irrtum bzw. (von Null verschiedener) “Schätzfehler” wohl nicht nur auf die an sich exakten “Umfragewerte aus Stichproben von jeweils 1000 Befragten” an sich,
sondern auf deren (jeweilige) Differenz zu einem “Kennwert”, der die Gesamtheit charakterisiert, aus der die Stichprobe genommen wurde;
d.h. den “Mittelwert p der (veranschlagten) Verteilung von (ggf. nur fiktiven) Umfragewerten”.
Also halte ich die im obigen Beitrag gezeigte Hypothesenformulierung (“Schritt 2.“) für korrekturbedürftig.
> Soviel ich weiß, kann man die Nullhypothese nicht bestätigen oder beweisen. Bei einer Nicht-Ablehnung der Nullhypothese wird diese streng genommen weder unterstützt, noch wird die Gegenhypothese unterstützt. […] Man könnte jetzt auf den Fehler 2. Art schauen. […]
Dem stimme ich streng genommen zu.
Was sich angesichts (eventuell sogar fortgesetzter) Stichprobennahme und -auswertung nicht ablehnen ließ,
mag aber euphemistischer immerhin “erprobt und (zunehmend) hinnehmbar” genannt werden.
p.s.
SciLogs-Kommentar-HTML-Test:
“H<sub>0</sub>” wird dargestellt als: “H0”.
p.p.s.
SciLogs-Kommentar-LaTeX-Test:
“\) H_0 \* ” wird dargestellt als “\( H_0 \)”.
@ Herr Dr. Wappler :
Sie liegen hier “ganz schwer” falsch.
Oder war’s Ironie?
Die sogenannte Statistische Signifikanz (hier werden in der Tat Zeichen gesetzt) ist bei einem Signifikanzniveau von 5% “nur” Konfidenzintervalle bereit stellend und hat nichts mit Wahrheit zu tun, vergleiche mit Ihrem ‘dann wäre die Hypothese offensichtlich falsch’.
Am Rande notiert, abär doch wichtich :
Statistisch getestete Hypothesen werden nie bestätigt, es wird vom Statistiker nur zum Vergleich angeboten, in einem bestimmten Modell-Zusammenhang, dass bestimmte Ergebnisse, die auf Messungen beruhen, mit bestimmter Zufälligkeit ebenfalls entstanden sein könnten, genau so.
MFG + HTH (“Hope to Help”) + schöne Woche noch,
Dr. Webbaer (der natürlich ebenfalls am Wesen der Statistik wie an dem der Stochastik zu nagen hat – immerhin funktioniert derartige Vorgehensweise irgendwie und generiert wirtschaftlichen Nutzen regelmäßig)
Dr. Webbaer schrieb (5. September 2017 @ 22:25):
> […] es wird vom Statistiker nur zum Vergleich angeboten, in einem bestimmten Modell-Zusammenhang, dass bestimmte Ergebnisse, die auf Messungen beruhen, mit bestimmter Zufälligkeit ebenfalls entstanden sein könnten
Ganz recht.
Meines Erachtens würde solch ein Statistiker die in Betracht stehende Hypothese deshalb folgendermaßen formulieren:
Also ausdrücklich nicht wie Joe Dramiga im obigen SciLogs-Beitrag:
Noch Fragen? …
p.s.
SciLogs-Kommentar-HTML-Test:
“H<sub>0</sub>” wird dargestellt als: “H0”.
p.p.s.
SciLogs-Kommentar-LaTeX-Test:
“\( H_0 \)” wird dargestellt als “\( H_0 \)”.
p.p.p.s.
Obwohl ich die mittlerweile offenbar zur Auswahl gestellte SciLogs-Kommentarvorschau in einigen anderen Fällen schon erfolgreich benutzt habe, funktioniert sie für mich (bzw. meinen Browser) im Moment leider nicht …
@ Herr Dr. Wappler :
Kein direkt dummer Vorschlag, aber vermutlich dürfen statistisch zu testende Hypothesen möglichst konkret, möglichst hart sein.
Zu beachten bleibt in diesem Zusammenhang die generell aus wirtschaftlichen Gründen zu geringe Größe der Datenprobe und das Verkaufsziel des Anbieters statistischer Leistung.
Gerade politische Meinungsumfragen leiden zurzeit und zunehmend daran, dass sich Abgefragte verstellen. Dr. W hätte hier keine Probleme und wäre bspw. pro Trump, pro Brexit und pro AfD (ohne diese Partei als direkt liberal anzuerkennen, aber die FDP zu wählen bedeutete (per se amoralische, vs. unmoralische) Wirtschaftsinteressen zu wählen, Liberale wollen aber liberal wählen).
Zum Glück darf Dr. Webbaer gar nicht wählen.
MFG
Dr. Webbaer
Statistiker-Hypothese:
Ich kann leider nicht nachvollziehen, weshalb ich für mein Beispiel die Statistiker-Hypothese verwendet werden sollte.
1. Es geht nicht um ein hypothetisches (großes) p der Grundgesamtheit (61,5 Millionen Wahlberechtigte) das 50 % sein soll, sondern um ein tatsächliches (kleines) p das sich aus einer bestimmten Stichprobe (1000 Wahlberechtigte) ergab.
2. In meinem Beispiel ist der Umfragewert einer Stichprobe selbst kein Mittelwert. Nirgendswo wird in meinem Beispiel das (arithmetische) Mittel der Umfragewerte der Stichproben gebildet. Hier sollen nur die Umfragewerte zukünftiger Stichproben mit dem Umfragewert einer vergangenen Stichprobe verglichen werden – nichts soll gemittelt werden.
3. Deine Statistiker-Hypothese spricht von einem Mittelwert der Verteilung. Wie kann es ohne Mittelwert, ohne Varianz, ohne Standardabweichung diese Verteilung geben?
4. Wenn die Wahlentscheidung jedes einzelnen Wahlberechtigten konsistent (dauerhaft, sich nicht verändernd) ist, – eine Annahme, die in meinem Beispiel nicht vorkommt – warum sollte der Meinungsforscher da überhaupt eine Umfrage mit mehreren monatlichen Stichproben machen?
Ich glaube, Du hast ein anderes Szenario als mein Beispiel im Kopf.
Joe Dramiga schrieb (6. September 2017 @ 16:36):
> 1. Es geht nicht um ein hypothetisches […] p der Grundgesamtheit (61,5 Millionen Wahlberechtigte) das 50 % sein soll
Wir können aber festhalten, dass genau dieses “p der Grundgesamtheit (61,5 Millionen Wahlberechtigte)” dennoch definierbar ist und sich konkrete Werte dieser Größe als konkrete Modellfälle bzw. Hypothesen ansetzen lassen.
> 3. Deine Statistiker-Hypothese spricht von […] Verteilung. […]
Relevant ist genaugenommen die Hypergeometrische Verteilung.
Die ist durch die drei gegebenen bzw. angesetzten Parameter (Grundgesamtheit N = 61,5 Millionen, Stichprobengröße n = 1000 und Erwartungswert z.B. n p = 500) jeweils vollständig festgelegt;
und (Überraschung?) ist für die hier in Betracht stehenden Größenordnungen der Parameterwerte von der entsprechenden Binomialverteilung kaum zu unterscheiden.
> 4. Wenn die Wahlentscheidung jedes einzelnen Wahlberechtigten konsistent (dauerhaft, sich nicht verändernd) ist […]
Mit “konsistent” meinte ich oben, dass diese Verteilung, die im Sinne einer Häufigkeits-Verteilung ja die Umfragewerte (x = k/n) aus “N über n vielen” verschiedenen denkbaren (fiktiven) Stichprobenahmen zusammenfassend darstellt, durch lediglich die drei genannten Parameterwerte (N, n, p) jeweils vollständig beschrieben ist.
Dabei bleibt es (natürlich) trotzdem denkbar, dass die Grundgesamtheit bei verschiedenen tatsächlichen Stichprobenahmen durch verschiedene Werte p charakterisiert gewesen wäre. Gerade deshalb stellt sich ja die im obigen SciLogs-Beitrag angedeutete Frage, ob und in wie fern von Stichprobe zu Stichprobe (Index “j”) i.A. sowieso veränderliche Umfragewerte (x_j = k_j / n) eine Änderung der Präferenz der Grundgesamtheit (“Wählergunst p”) signalisieren.
So weit zu dem Szenario, an dass ich denke, wenn ich (im obigen SciLogs-Beitrag) lese: “Wahlkampfstatistik ist Inferenzstatistik, die anhand von Stichproben Aussagen über die Grundgesamtheit der Wahlberechtigten macht.”,
> Ich glaube, Du hast ein anderes Szenario als mein Beispiel im Kopf. […]
> 1. […] sondern [es geht] um ein tatsächliches (kleines) p das sich aus einer bestimmten Stichprobe (1000 Wahlberechtigte) ergab.
Der Umfragewert x_0 = k_0 / n = 500 / 1000 der anfänglichen Umfrage (siehe oben Fußnote 1) wurde oben “Schritt 1. Erwartungswert festlegen:” offenbar der Größe p_0 zugeschrieben.
Der Erwartungswert welcher Verteilung soll denn dadurch abgeschätzt worden sein, wenn nicht der beschriebenen Häufigkeits-Verteilung von Umfragewerten aus allen (mit Ausnahme der einen anfänglichen Umfrage alle fiktiven) denkbaren Stichprobennahmen aus der Grundgesamtheit?
Was soll der Wert von p_0 denn darstellen, wenn nicht gerade eine (erste, begründete) Vermutung betreffend den Wert von “p der Grundgesamtheit (61,5 Millionen Wahlberechtigte)“?
> 2. In meinem Beispiel ist der Umfragewert einer Stichprobe selbst kein Mittelwert. Nirgendswo wird in meinem Beispiel das (arithmetische) Mittel der Umfragewerte der Stichproben gebildet.
Dennoch erfolgte “Schritt 1. Erwartungswert festlegen:“.
> Hier sollen nur die Umfragewerte zukünftiger Stichproben mit dem Umfragewert einer vergangenen Stichprobe verglichen werden
Das entspricht ja auch offenbar der oben im SciLogs-Beitrag gezeigten “Hypothesenformulierung […] Der Umfragewert […] beträgt unverändert 50 %.“.
Wenn aber nur und genau das so gemeint wäre, dann erscheinen die obigen Betrachtungen zu “Signifikanzniveau“, “Irrtumswahrscheinlichkeit“, “Ablehnungsbereich” und “Entscheidungsregeln” völlig überflüssig. Denn nur die natürliche Zahl 500 ist gleich der (in der anfänglichen Umfrage gefundenen) exakten natürlichen Zahl 500;
alle anderen natürlichen Zahlen sind schlicht und eindeutig ungleich 500.
p.s.
SciLogs-Kommentar-HTML-Test:
“H>sub<0>/sub<” wird dargestellt als: “H0”.
p.p.s.
SciLogs-Kommentar-LaTeX-Test:
“\( H_0 \) ” wird dargestellt als “\( H_0 \)”.
Wieder vely klug angemerkt, Sie sind Der geborene “Datenjournalist”, lieber Herr Dr. Dramiga.
Sie haben die Statistik in ihrer Funktionalität verstanden, etwas, das von anderen nicht behauptet werden kann.
Womöglich haben Sie auch die Stochastik, die Ratelehre, verstanden?
—
Ansonsten könnte klar sein, dass es Wirtschaftlichkeitsüberlegungen sind, die die politische Meinungsforschung antreiben, die Datenproben grundsätzlich zu klein ausfallen lassen.
Bei politischen Meinungsumfragen ist zudem auch immer die Rolle des Auftraggebers zu beachten, die vermutete Rolle.
In der Naturlehre wie auch im Unternehmerischen wird ja auch eher in “Sigma” gemacht, bspw. so :
-> https://de.wikipedia.org/wiki/Six_Sigma
“Sigma” ist insofern der Sache angemessener, wenn Versuche (“Messungen”) zigfach und wirtschaftlich tauglich millionen-, milliarden- und billionenweise (u.s.w.) wiederholt werden können.
MFG + vielen Dank + weiterhin viel Erfolg,
Dr. Webbaer
Natürlich kannst Du beliebig a priori ein p der Grundgesamtheit definieren. Nur was hat das mit meinem Beispiel zu tun? In meinem Beispiel wird p a posteriori (durch Stichprobe) festgelegt.
Genaugenommen ist die hypergeometrische Verteilung nicht relevant für mein Beispiel. Bei der hypergeometrischen Verteilung werden die Stichproben nicht wieder in das Reservoir zur erneuten Befragung zurückgelegt – im Gegensatz zur Binomialverteilung in meinem Beispiel. Das heißt deine Stichprobennahme würde theoretisch irgendwann zu Ende sein, während man bei meinem Beispiel theoretisch unendlich oft eine Stichprobe nehmen könnte. Nur weil in meinem Beispiel der Stichprobenumfang n im Verhältnis zur Grundgesamheit N relativ klein ist, unterscheiden sich die durch die Binomialverteilung bzw. die hypergeometrische Verteilung berechneten Wahrscheinlichkeiten nicht wesentlich voneinander.
Warum dann Statistik betreiben? Geht es nur darum, ob ein Umfragewert 500 ist oder nicht? Die Anzahl der Erfolge in einer Serie von gleichartigen und unabhängigen Versuchen, die jeweils genau zwei mögliche Ergebnisse haben („Erfolg“ oder „Misserfolg“). Solche Versuchsserien werden auch Bernoulli-Prozesse genannt. Sie werden durch die Binomialverteilung beschrieben.
Die Wahrscheinlichkeit, dass der Umfragewert nicht 500 ist, wäre 999/1000. Die drei Zahlen 5, 480, 900 sind nicht 500. Jede dieser drei Zahlen hätte die gleiche Wahrscheinlichkeit des Auftretens: ein Tausendstel, wie bei einem 1000-seitigen Würfel. Die Wahrscheinlichkeitsverteilung dieses Würfels ist nicht hypergeometrisch und hat auch nichts mit meinem Beispiel zu tun.
Joe Dramiga schrieb (7. September 2017 @ 00:57):
> [Denn nur die natürliche Zahl 500 ist gleich der (in der anfänglichen Umfrage gefundenen) exakten natürlichen Zahl 500; alle anderen natürlichen Zahlen sind schlicht und eindeutig ungleich 500.]
> Warum dann Statistik betreiben? Geht es nur darum, ob ein Umfragewert 500 ist oder nicht?
Berechtigte Fragen. Eben.
Genau das frage ich mich nach wie vor angesichts des Wortlauts des obigen SciLogs-Beitrags:
Diese “Hypothesenformulierung” passt meines Erachtens jedenfalls nicht zur einführend thematisierten “Wahlkampfstatistik […], die anhand von Stichproben Aussagen über die Grundgesamtheit der Wahlberechtigten macht.“;
und möglicher Weise passt sie nicht einmal zu den Statistik-Betrachtungen im Rest des Beispiels des obigen SciLogs-Beitrags.
Und ich wundere mich zunehmend, warum an genau dieser schon mehrfach beanstandeten “Hypothesenformulierung” festgehalten wird …
So weit zur Hauptanliegen meiner Kommentare auf dieser Seite.
Nun zu weiteren Themen:
> Die Wahrscheinlichkeit, dass der Umfragewert nicht 500 ist, wäre 999/1000. Die drei Zahlen 5, 480, 900 sind nicht 500. Jede dieser drei Zahlen hätte die gleiche Wahrscheinlichkeit des Auftretens: ein Tausendstel, wie bei einem 1000-seitigen Würfel.
Das träfe zu, wenn diese Werte (Wertebereich natürliche Zahlen 0 bis 1000) gleichverteilt wären; bzw. wenn der entsprechende 1001-seitige Würfel “gut/fair” wäre.
Wenn wir uns dagegen vorstellen, dass die Umfragewerte (Wertebereich natürliche Zahlen 0 bis 1000) entsprechend einer hypergeometrischen verteilung mit Erwartungswert p = 0,500, Grundmenge N = 61,5 Millionen und konstanter Stichprobengröße n = 1000 gefunden werden,
oder auch entsprechend der nahezu gleichen Binominalverteilung,
dann ist es erheblich wahrscheinlicher, den Wert 500 zu erhalten (bzw. auch in wiederholten Stichprobennahmen zu erhalten) als z.B. den Wert 5.
> Bei der hypergeometrischen Verteilung werden die Stichproben nicht wieder in das Reservoir zur erneuten Befragung zurückgelegt – im Gegensatz zur Binomialverteilung
Es stimmt zwar, dass sich die hypergeometrische Verteilung aus den sogenannten “Kombinationen ohne Zurücklegen bzw. ohne Wiederholung” ergibt;
und die Binomialverteilung aus “Kombinationen mit Zurücklegen bzw. mit Wiederholung“.
Diese Unterscheidung betrifft aber nicht das (mehrfache, fortgesetzte) Einbehalten ganzer Stichproben, oder andernfalls das jedesmalige Zurücklegen ganzer Stichproben;
sondern das Einbehalten von gezogenen Objekten jeweils innerhalb einer Stichprobennahme, oder andernfalls das jedesmalige Zurücklegen jedes einzelnen gezogenen Objekts vor der nächsten Ziehung jeweils innerhalb einer Stichprobennahme.
Eine einzelne Stichprobennahme besteht hier aus 1000 einzelnen “Ziehungen” (d.h. jeweils Auswahl eines einzelnen Befragungsteilnehmers aus der Grundgesamtheit, mit anschließender Befragung, ob der betreffende Wahlberechtigte “pro” oder “con” ist).
Bei “Kombinationen ohne Zurücklegen/Wiederholung” soll ausgeschlossen sein, dass innerhalb dieser einen Stichprobennahme ein-und-der-Selbe bestimmte identifizerte Wahlberechtigte mehrfach ausgewählt und befragt würde; oder dass gar mehrere bestimmte Wahlberechtigte mehrfach gezogen würden.
Diejenigen, die im Laufe einer Stichprobennahme schon einmal gezogen/ausgewählt/befragt wurden, bleiben deshalb von erneuter Auswahl/Befragung ausgeschlossen, d.h. “einbehalten” (also nicht “in die Grundmenge zurückgelegt”), bis der letzte (d.h. der tausendste) einzelne Teilnehmer der Stichprobe gezogen wurde.
Bevor die nächste Stichprobe genommen wird (sei es tatsächlich, oder nur gedanklich) würde die “Urne” aber wieder entsprechend der veranschlagten Grundgesamtheit aufgefüllt.
(In den betreffenden Wikipedia-Artikeln habe ich dieses Verständnis zwar nicht ausdrücklich formuliert gefunden; aber auch nichts, was dem widerspräche.)
> Das heißt deine Stichprobennahme würde theoretisch irgendwann zu Ende sein
Nein: Stichproben (d.h. je 1000 einzelne Ziehungen/Befragungen) können also aus beiden Verteilungen zumindest gedanklich beliebig oft genommen werden.
> Natürlich kannst Du beliebig a priori ein p der Grundgesamtheit definieren. Nur was hat das mit meinem Beispiel zu tun? In meinem Beispiel wird p a posteriori (durch Stichprobe) festgelegt.
Die Definition einer Größe
ist zu unterscheiden
von der Ermittlung oder Abschätzung oder Annahme eines bestimmten Wertes dieser Größe.
(Die Definition einer Messgröße durch einen bestimmten nachvollziehbaren Messoperator
ist zu unterscheiden von
der Ermittlung des Wertes dieser Größe in einem bestimmten Versuch durch Anwendung des definierten Messoperators auf die Beobachtungsdaten des Versuchs;
und von der Abschätzung oder Annahme des Wertes dieser Größe durch Einsatz anderer Methoden.)
Wie in meinem vorausgegangenen Kommentar dargestellt, lässt sich der Umfragewert “0,500” der anfänglichen Umfrage zumindest als erste Abschätzung des Erwartungswertes p der Grundgesamtheit nutzen;
und das erinnert doch sehr an den obigen “Schritt 1. Erwartungswert festlegen: […] ”
Abschließend möchte ich betonen, dass mich Artikel wie der obige bzw. Kommentar-Rückmeldungen wie die vorliegenden besonders deshalb freuen und zur sorgfältigen Beschäftigung anregen, weil bzw. sofern SciLogs die Möglichkeit der Barriere-freien öffentlichen und zeitnahen Stellungnahme eröffnet.
Und vielleicht wird ja eines Tages sogar die SciLogs-Kommentarvorschau klappen, und Hoch- bzw. Tiefstellung in SciLogs-Kommentaren.
p.s.
SciLogs-Kommentar-HTML-Test:
“H<sub>0</sub>” wird dargestellt als: “H0”.
p.p.s.
SciLogs-Kommentar-LaTeX-Test:
“\( H_0 \)” wird dargestellt als “\( H_0 \)”.
Dreimal der gleiche Kommenntar? Ich werde mal die zwei früheren Kommentare löschen.
Frank Wappler schrieb (7. September 2017 @ 12:07):
> [Zum] Hauptanliegen meiner Kommentare auf dieser Seite […]
> warum an genau dieser schon mehrfach beanstandeten “Hypothesenformulierung” festgehalten wird …
An geeigneten Mitteln darzustellen, dass eine bestimmte Formulierung gelassen und eine andere genommen wurde, soll es jedenfalls nicht scheitern; z.B. so:
“2. Hypothesenformulierung
Nullhypothese:
Der Umfragewert für Schulz beträgt unverändert 50 % = 0,50.Der Erwartungswert der Verteilung aller Umfragewerte für Schulz aus allen denkbaren, hypothetisch jeweils einmal genommenen Stichproben beträgt unverändert 50 % = 0,50.”
p.s.
SciLogs-Kommentar-HTML-Test:
“<sub>0</sub>” wird dargestellt als: “0”.
p.p.s.
SciLogs-Kommentar-LaTeX-Test:
“\( H_0 \)” wird dargestellt als “\( H_0 \)”.
Joe Dramiga schrieb (7. September 2017 @ 15:25):
> Dreimal der gleiche Kommentar?
Die drei Versionen meines Kommentars waren natürlich nicht exakt gleich; sonst hätte die SciLogs-Software erfahrungsgemäß gar nicht zugelassen, dass ich mehrere davon einreiche. Sie waren an einer bestimmten Stelle sogar erheblich verschieden formuliert.
Und ich war nicht nur mit meiner Formulierung in der ersten Version im Nachhinein unzufrieden, sondern sogar in der zweiten; was mich allerdings (leider, auch mangels funktionierender Kommenvorschau) jeweils erst bei Ansicht nach dem Absenden dazu bewog, die entsprechende Formulierung weiter zu verändern.
> Ich werde mal die zwei früheren Kommentare löschen.
Danke, das begrüße ich.
(In vergleichbaren Fällen habe ich auch schon die Erfahrung gemacht, dass andere, die zur Löschung von Sciogs-Kommentaren in der Lage gewesen wären, solches Entgegenkommen nicht zeigten.)
Allerdings wäre es auch denkbar und wünschenswert, den Kommentatoren selbst die Möglichkeit zu geben, Kommentarversionen wahlweise zu ersetzen. Zur Authentifizierung könnte ja z.B. die “Email”-Angabe des betreffenden Kommentars dienen.