Nachdem ich jüngst in einem Beitrag wieder die Wichtigkeit von Überschlagsrechnungen erwähnt hatte und andererseits neulich zufällig wieder bei Wolfram Alpha vorbeikam, habe ich mich gefragt, ob Wolfram Alpha nicht ein gutes Werkzeug für solche Rechnungen ist – sowohl während der Rechnung als auch beim Überprüfen der Antwort.

Nach eigenem Anspruch will Wolfram Alpha mehr sein als eine Suchmaschine, nämlich eine Wissensmaschine – idealerweise so etwas wie der Computer bei Raumschiff Enterprise, dem man alle für die Mission wichtigen Fragen stellen kann und der dann sinnvolle Antworten gibt.

Bei einfachen Fragen funktioniert das auf alle Fälle. Auf die Anfrage “volume 2 by 2 by 2 m” hin sagt Wolfram Alpha, wie es die Eingabe interpretiert hat (“Quader Seitenlängen 2m 2m 2m”), gibt das Volumen, eine grafische Skizze, das Volumen in anderen Einheiten (Liter, Gallonen, Kubikfuß) und einige interessante Vergleichswerte (entsprich 45% des Volumens eines Grauwals).

Bereits das ist deutlich intelligenteres Verhalten als z.B. bei Google, das mir bei der gleichen Anfrage ziemlich sinnlose Links (Top-Treffer: “F*** Me I’m Famous Vol.2”, aus welchen Gründen auch immer) liefert.

Auch einiges an Physik kennt Wolfram Alpha. “time dilation at 0.999 c” wird richtig erkannt als Frage zur speziell-relativistischen Zeitdilatation, und das Programm ermittelt und antwortet, wie die Eigenzeit eines mit 99,9% Lichtgeschwindigkeit Reisenden von einem außenstehenden Beobachter wahrgenommen wird. Dass das Programm bei 99,999% Lichtgeschwindigkeit bereits auf 1.0, also auf volle Lichtgeschwindigkeit aufrundet, ist allerdings schade – die Fälle mit immer mehr Neunen sind gerade in diesem Fall ja durchaus interessant.

Direkt bei der Mathematik ist Wolfram Alpha ziemlich leistungsfähig. Das überrascht nicht, ist es doch ein Kind von Stephen Wolfram, einem der Pioniere der Computeralgebra und Vater des weit verbreiteten Computeralgebra-Programms Mathematica. Eine Frage wie “integrate from 0 to infty x^2 exp(-x^2)”, also das Integral von Null bis Unendlich der Funktion x² exp(-x²), bekommt Wolfram Alpha ohne weiteres hin. Bei komplizierteren Integralen stößt man manchmal an das eingebaute Zeitlimit (das für Pro-Benutzer [$5,49 pro Monat] länger ist als für Gelegenheitsnutzer).

Für Überschlagsaufgaben ist praktisch, dass Wolfram Alpha viel Faktenwissen hinterlegt hat. Bei Überschlagsaufgaben, etwa den berühmten Fermi-Problemen, geht es ja darum, ohne großes Rechnen eine sinnvolle Abschätzung vorzunehmen – sei es um eine ungefähre Idee zu bekommen, in welche Richtung eine genauere Analyse gehen sollte, sei es als Konsistenzprüfung, sei es einfach um ein Gefühl dafür zu bekommen, worum es bei dem Problem geht.

Solche Abschätzungen sind Gold wert, um quantitatives Verständnis für ein Fach oder eine Situation zu bekommen; hier auf den SciLogs schreibt Joe Dramiga gelegentlich etwas in diese Richtung, drüben bei den Sciencelogs haben z.B. Florian Freistetter und Martin Bäker etwas zum Thema gemacht, ich hier ja auch mehrmals (Mondlicht-Fotozellen, Kirchhof-Steuermodell, regenerative Energien, Fukushima). Auch Unternehmensberatungen nutzen Fermi-Probleme, so hört man gelegentlich, in ihren Auswahlgesprächen – durchaus sinnvoll, geht es doch schließlich darum, aus komplexen Situationen mit intelligenter Vereinfachung eine Schätz-Antwort abzuleiten; wer ein Unternehmen und dessen Potenziale, Märkte, Effizienz verstehen möchte, für den stecken solche Schätzungen einen sinnvollen Rahmen ab.

Die Klavierstimmer

Der Klassiker der Fermi-Probleme ist die Frage, wieviele Klavierstimmer es in Chicago gibt. Dazu kann man ungefähr so argumentieren. Klaviere sind nicht allzu häufig – in meinem Bekanntenkreis hat nur jeder zehnte bis zwanzigste ein Klavier, würde ich schätzen; bei Menschen mit weniger Einkommen sind sie wahrscheinlich noch seltener, sagen wir: jeder fünfzigste besitzt ein Klavier. Jetzt die erste Frage an Wolfram Alpha:

“how many inhabitants in Chicago?”

wird verstanden und gibt 2.7 Millionen Einwohner für Chicago, also rund 50.000 Klaviere. Wer sein Klavier liebt und es sich leisten kann, dürfte es mindestens einmal pro Jahr stimmen lassen; tatsächlich sind es wahrscheinlich weniger; nehmen wir im Durchschnitt mal an, dass jedes Klavier nur alle zwei Jahre gestimmt wird (ein Mittelwert aus den Klaviervernachlässigern und den mit hinreichenden Mitteln ausgestatteten Klavierliebhabern).

Das bringt uns zu 25.000 Stimmvorgängen pro Jahr. Ich schätze andererseits, dass es kaum mehr hauptamtliche Klavierstimmer geben dürfte, die tatsächlich nichts anderes tun als stimmen, stimmen, stimmen (allenfalls vielleicht einige vernachlässigbar wenige, die jeden Tag in den Chicagoer Konzerthäusern unterwegs sind und vermutlich bereits davon leben können). Wahrscheinlicher scheint mir, dass die Klavierstimmer auch Reparaturen durchführen, an ein Klaviergeschäft angeschlossen sind, jedenfalls nicht ihre ganze Zeit nur mit dem eigentlichen Stimmen verbringen. Schätzung: Diese Menschen stimmen nur ein bis zwei Klaviere pro Arbeitstag, also rund 400 Klaviere pro Jahr. Damit komme ich auf etwas mehr als 60 Klavierstimmer in Chicago.

Andere Fermi-Problemlöser kommen auf etwas andere Zahlen; das ist aber OK. Es geht vor allem um Größenordnungen und darum, zu verstehen, welche Faktoren beim Zustandekommen der Zahl eine Rolle spielen.

Fragt man Wolfram Alpha selbst,

“how many piano-tuners in Chicago?”

liefert die Maschine übrigens die allgemeinere Antwort, es gebe 290 Menschen, die als “musical instrument repairers and tuners” in Chicago beschäftigt seien. Bedenkt man, dass dabei auch Geigenbauer, Blasinstrumentenreparateure, Orgelstimmer etc. sind, kommt das wahrscheinlich ungefähr hin.

Ein Beispiel aus der Kosmologie

Mal ein spezialisierteres Beispiel, nämlich eine Abschätzung, ab welcher Temperatur im frühen Universum Wasserstoffatome existieren können – das ist die Temperatur, bei der die kosmische Hintergrundstrahlung entstanden ist.

Dazu muss ich wissen, wieviel Energie nötig ist, um ein Wasserstoffatom zu ionisieren. Diejenigen Lichtteilchen = Photonen, die das Ionisieren erledigen, sind Photonen der Wärmestrahlung, die das frühe Universum erfüllte. Wieviele der Photonen mehr als eine gegebene Energie besitzen, ist durch die sogenannte Planck-Verteilung geregelt. Als weitere Information nehme ich hinzu, dass es für jedes Wasserstoffatom rund 2 Milliarden Photonen gibt, und dass das Gemisch aus Atomen (ionisiert und unionisiert) und Photonen so dicht ist, dass gilt: Wenn ein Photon mit ausreichender Energie da ist um ein Wasserstoffatom zu ionisieren, dann wird dieses Photon auch ein Wasserstoffatom ionisieren.

Dann muss ich nur noch wissen: Wie hoch ist bei gegebener Temperatur der Anteil von Photonen mit mehr als der für die Ionisierung nötigen Energie?

Eigentlich ein einfaches Abschätzungsproblem.

Die Ionisationsenergie von Wasserstoff kennt Wolfram Alpha, allerdings habe ich Schwierigkeiten, die Antwort als Energie pro Atom zu bekommen – selbst wenn ich “What is the ionisation energy of a single hydrogen atom?” frage, bekomme ich die Antwort in Kilojoule pro Mol.

Immerhin kann man Ergebnisse kopieren (“Copyable plaintext” unter jedem Ergebnis), und im nächsten Schritt gibt mir

“1312 kJ / Avogadro’s number in eV”
immerhin die richtige Antwort von 13,6 Elektronvolt, allerdings deutlich langsamer, als wenn ich stattdessen direkt in Wikipedia nachgeschaut hätte.

Das frühe Universum war von energiereichen Photonen angefüllt, einer fast perfekten Wärmestrahlung. Deren Energieverteilung folgt der sogenannten Planck-Verteilung.

Schauen wir mal, ob Wolfram Alpha das kann.

“average photon energy at temperature 1000 K”

bekommt die Maschine in den falschen Hals. Irgendwie scheint sie zu glauben, es ginge um die Temperatur in 1000 km Höhe über dem Erdboden, und parallel dazu um die Ruhemasse (bzw. Ruheenergie) von Photonen.

“planck distribution photon energy at 1000 Kelvin”

liefert immerhin eine interaktive Tabelle, bei der man in die Planck-Formel eine Temperatur (1000 Kelvin wird nicht automatisch übernommen!), untere und obere Wellenlänge einsetzen kann und die spektrale Energiedichte zurück bekommt. Aber mich interessiert eigentlich die Zahlendichte: Wieviele Photonen gibt es, die eine Energie von mehr als 13,6 Elektronvolt haben?

Versuchen wir’s mal Schritt für Schritt:

“planck distribution number density”

Keine Chance. Diese beiden Konzepte bringt Wolfram Alpha einfach nicht zusammen.

Kann Wolfram Alpha wenigstens helfen, wenn man’s per Hand versucht und dem Computer nur das rechnen überlässt?

Um mal aus meinen Vorlesungsfolien für den gerade zuende gegangenen Kosmologie-Blockkurs zu kopieren: Aus der Planck-Formel kann man die Zahl der Photonen mit mehr Energie als mkT (m eine ganze Zahl, k die Boltzmann-Konstante, T die Temperatur in Kelvin) bei Wärmestrahlung berechnen zu

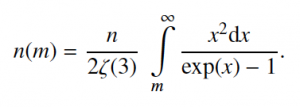Dabei ist n die Gesamtzahl der Photonen und Zeta(3) die Riemann’sche Zetafunktion, ausgewertet für das Argument drei.

Eine Möglichkeit, Wolfgang Alpha zu sagen, dass ich wissen will, für welches m der Anteil n(m)/n gerade ein Zweimilliardstel ist, habe ich nicht gefunden. Also probiere ich aus, indem ich verschiedene m-Werte einsetze, und fange mit 5 an:

“integrate from 5 to infty x^2/(exp(x)-1)”

führt aber nur dazu, dass Wolfram Alpha die Formel schön hinschreibt. Auch

“numerically integrate from 5 to infty  x^2/(exp(x)-1)”

gibt kein anderes Ergebnis. Bei den bisherigen Beispielen war schön, dass ich Wolfram Alpha direkt in fast natürlicher Sprache sagen konnte, was es tun sollte.

Dann also anders: Um herauszufinden, ob Wolfram Alpha hier eine bestimmte Syntax bei der Eingabe benötigt google ich etwas und finde diese Seite hier zu numerischer Integration.

Bei

“Simpson’s rule x^2/(exp(x)-1) on [5,infinity] interval size 0.5”

denkt Wolfram Alpha aber entgegen der Ausführungen auf erwähnter Hilfe-Seite, es solle die Funktion plotten. Bei der Trapezregel wird es nicht besser. Die Unendlichkeit am oberen Ende scheint das System komplett durcheinander zu bringen.

Bei meiner Vorlesungsvorbereitung hatte ich den Wert mit dem mpmath-Paket für Python ausgerechnet; dazu gibt es bei der SageMathCloud auch ein Web-Interface (für das man ein kostenloses Konto anlegen muss).  Das Ergebnis dort war gewesen, dass eine Milliardstel der Photonen eine Energie von 27 kT oder mehr besitzen. Das hätte ich gerne auch mit Wolfram Alpha herausbekommen.

Setzt man den Wert ein, dann kommt man darauf, dass für eine Temperatur von 5845 Kelvin und höher nach unserem vereinfachten Kriterium alle Wasserstoffatome durch die anwesenden Photonen ionisiert sind.

Nahe bei dieser Temperatur (in Wirklichkeit: erst bei knapp 3000 K, also ein Faktor 2 weniger) kann man erwarten, dass sich Protonen und Elektronen zu Wasserstoffatomen zusammenfinden.

Fazit

Wolfram Alpha gibt einen ersten Vorgeschmack darauf, wie Computer in hoffentlich nicht allzu ferner Zukunft beim Nachdenken und Abschätzen helfen können – aber es ist bis dahin noch ein weiter Weg. Wenn Computer dann einmal soweit sind, dass sie interaktiv beim Nachdenken über mathematische und naturwissenschaftliche Fragestellungen helfen können, wird das sicher eine spannende Zeit – wer diese Art von Interaktion beherrscht, kann viel schneller ausprobieren, sich zeigen lassen, simulieren lassen worum es geht. Das ist wohlgemerkt ein viel weniger schweres Problem als wirklich intelligente Computer zu bauen, die den Turing-Test bestehen, mit ihren menschlichen Gegenübern philosophieren können und was weiß ich alles. Insofern bin ich durchaus zuversichtlich, was die Zeitskala angeht: 5 Jahre? 10 Jahre? Wir werden sehen.