Physik ist wie Schach – nicht wie ein Puzzle
BLOG: RELATIV EINFACH

Ich halte derzeit zusammen mit einem Kollegen von der Uni (Björn Malte Schäfer) die Vorlesung “Kosmologie für Nichtphysiker” die, wie der Name sagt, Nichtphysikern – in der Vorlesung sitzen Studierende der Theologie, Psychologie, Anglistik u.ä., außerdem eine Reihe interessierter Gasthörer – die kosmologischen Modelle der modernen Astrophysik nahezubringen. Für mich ist das eine sehr spannende Veranstaltung, da sie einen höheren Anspruch hat als z.B. ein populärwissenschaftlicher Vortrag, andererseits aber nicht zuviel Mathematik und Physik voraussetzen darf. Dass dafür dann im Vergleich zu Vorträgen viel Zeit zur Verfügung steht – ein Termin pro Woche über ein Semester hin – schafft die Voraussetzungen dafür, trotz der Einschränkungen bis zu einer gewissen Tiefe gehen zu können und dabei z.B. auch Fragen nach der Methodik (woher wissen wir, was wir wissen?) anzusprechen.
In der vorvorletzten Vorlesung bin ich am Beispiel der Newton’schen Mechanik darauf zu sprechen gekommen, wie physikalische Naturgesetze funktionieren und wie nicht – sprich: was sie einschränken, und wo sie der Natur Freiheiten lassen. (Wer sich auskennt, wird ahnen: Es geht um Differentialgleichungen und die Möglichkeit, Anfangsbedingungen zu wählen.)
Besonders deutlich wurde für mich der Kontrast zwischen Newton’scher Physik und der Erklärung, die Johannes Kepler Ende des 16. Jahrhunderts dafür zu formulieren versucht hatte, warum die Abstände der Planeten im Sonnensystem so sind und nicht anders. 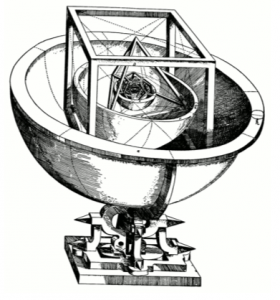
Kepler hatte sich (siehe Bild links) ein geometrisches Modell überlegt, in dem sich Abstände aus den Eigenschaften von regelmäßigen Vielflächnern (Würfel, Tetraeder etc.) ergeben: Es sind die Abstände, die man bekommt, wenn man immer abwechselnd einen dieser Vielflächner und eine Kugel ineinanderschachtelt wie eine geometrische Matrjoschka (Geomatrjoschka?).
Wie gut dieses Modell die Abstände im Sonnensystem erklären kann, ist die eine Frage; für mich war ein anderer Aspekt viel interessanter: Ein solches Modell erklärt die Abstände so, wie sie sind. Es gibt keine anderen Möglichkeiten. Die Erklärung, das Naturgesetz, legt fest, wie die Dinge sind.
Das ist eine beachtliche Einschränkung, und ein großer Kontrast zur Newton’schen Beschreibung. In Newtons Welt könnte das Sonnensystem auch ganz andere Abstandsverhältnisse aufweisen – allein Stabilitätsüberlegungen (ob sich Planeten bei einer bestimmten Abstandskonfiguration zu nahe kämen und sich aus dem Sonnensystem oder auf andere Bahnen lenken würden) schränken ein, was machbar ist. Die Newton’schen Gesetze legen eben nicht fest, was die Konfiguration der Welt ist, sondern lassen der Welt Freiheiten: Dass ein Objekt aus zwei Meter Höhe nach unten fällt ist mit ihnen genauso vereinbar wie dass es aus drei Meter fällt; dass seine Geschwindigkeit ursprünglich 20 km/h nach Osten betrug ebenso wie 40 km/h in Richtung Westen.
Newtons Gesetze sagen nur, welche Beschleunigungen sich aus der Wechselwirkung der Objekte (sei es durch Stoß oder durch längerreichweitige Kräfte wie Gravitation) ergeben. Welche Anfangsgeschwindigkeiten und Anfangsorte die beschriebenen Objekte haben, lässt sich frei vorgeben.
Für die Vorlesung viel zu spät (wie das immer so ist) ist mir noch eine einfache Analogie dazu eingefallen, die Björn dann noch etwas ergänzt hat, und das ist der Gegensatz zwischen Puzzlespiel und Schachspiel. Ein Puzzle gibt vor, wie das Endresultat auszusehen hat – zentrale Eigenschaft des Puzzles ist es, dass die Konfiguration der Spielwelt, das Aneinanderpassen der Puzzlestücke komplett vorgegeben ist.
Man vergleiche das mit Schach; da gibt es auch Regeln, aber sie betreffen im wesentlichen, wie sich Figuren bewegen können – nicht eine Einschränkung der Konfiguration, sondern der Art und Weise, wie sich die Spielwelt ändert.
Das Puzzle ist analog zu Keplers Beschreibung, Schach analog zur Newton’schen Physik – vorgegeben bei letzeren beiden sind Änderungsregeln, nicht Konfigurationen, und das macht die Möglichkeiten sehr, sehr vielfältig. Es erlaubt der Newton’schen Physik, viele verschiedene Situationen zu beschreiben, je nach den Anfangsvorgaben. Und es erlaubt atemberaubend viele mögliche Entwicklungen und Konfigurationen beim Schach.
Im Newton’schen Falle ist diese Vielfaltseigenschaft ein wichtiger Grund dafür, dass wir von allgemein gültigen Naturgesetzen reden. Wer Konfigurationen vorschreibt, bei dem ergibt sich aus dem “Gesetz” ein einziger Sonderfall. Erst die Vielfalt der Situationen, die mit der Newton’schen Mechanik beschrieben werden können, macht es sinnvoll, das Naturgesetz als Verallgemeinerung, als allgemein anwendbar, als in vielen Situationen gültig zu betrachten. Änderungsweisen einzuschränken, nicht Konfigurationen – das ist das Erfolgsrezept sowohl der modernen Physik als auch von Schach.


Ich finde den Vergleich mit Schach sehr schön. Insb. wenn man dann noch das klassische Schach und Chess960 ins Spiel bringt, bei dem die Grundstellung (die Anfangsbedingungen) ausgelost werden. Bei denselben Regeln ergeben sich ganz andere Spielverläufe (Planetenbahnen o.ä.).
Folgendes Zitat passt dann auch zur Physik: “Mathematik ist die Wissenschaft, welche aufzeigt wie man mit endlichen Mitteln das Unendliche bewältigt.“
Die endlichen Mittel, das sind ein paar Axiome, das Unendliche, das damit beschrieben wird, ist das Anwendungsgebiet dieser Axiome. Sehr gut passen hier die 3 Newtonschen Gesetze zu dieser Sicht. Etwas was offensichtlich bereits Newton als wichtig und herausstellenswert empfand, nannte er seine Abhandlung doch “Philosophiae Naturalis Principia Mathematica (Mathematische Prinzipien der Naturphilosophie)”. In der Physik wie in der Mathematik geht es also un ein Spiel dessen Regeln man entweder erfindet (Mathematik) oder findet (Physik).
Die Gültigkeit auch für einen infinitesimal kleinen Bereich begründet die Macht von Newton’s 3 Gesetzen der Bewegung (Axiomata sive leges motus), denn was für einen infinitesimal kleinen Bereich gilt, gilt für alles, gilt auch für einen beliebig grossen Bereich – unter der Annahme, die konzeptionell simple Summation und Superposition genügten um das Grosse mittels des im Kleinen gültigen zu beschreiben. Geleistet wird dieser Übergang von der von Newton mitbegründeten Infinitesimalrechnung. Philosophisch gesehen hat Newton mit diesem Gültigkeitsbereich vom Kleinsten bis zum Grössten dem Reduktionismus das wissenschaftliche Fundament gegeben, also der Überzeugung das Ganze könne verstanden werden, wenn man die Teile, die das Ganze ausmachen, verstehe. Es scheint, dass dies Newton sehr bewusst war, was sich etwa darin zeigt, dass es ihm wichtig war, die Integration über eine Kugel durchführen zu können. Sein Gravitationsgesetz war formuliert für punktförmige Masssen, doch mit der Summationsmöglichkeit (Integration) eben auch für Kugeln, also beispielsweise Planeten, Monde und Sterne, ja selbst für Erdlinge, die auf der Erdoberfläche stehen.
Die Newton’schen Gesetze sind aber auch ohne räumliche Integration, nur angewendet auf Punktmassen, bereits sehr mächtig, denn wir können ja auch über Zeitabschnitte oder zurückgelegte Wegstrecken integrieren (dW= F*ds). Die Superposition von Kräften wiederum schafft die Möglichkeit Kräfte auch dort zu sehen, wo die resultierende Kraft 0 ist und es somit gar keine Bewegung im Sinne der “Axiomata sive leges motus” gibt – also im statischen Fall.
Kurzum: Die eigentliche Macht der Newton’schen Bewegungsgesetze liegt in der Mathematik, die man hier anwenden kann, die man aber nur deshalb anwenden kann weil die auf mathematischer Ebene durchgeführten Summationen, Superpositionen und Integrationen eben nicht nur willkürliche, sondern “naturgerechte” Mathematik sind.
Dies noch zur Ergänzung zum
Newton’s Titel für sein Werk, nämlich “Mathematische Prinzipien der Naturphilosophie” zielt so gesehen auf den eigentlichen Kern dessen, was Newton begründet hat – und das beinhaltet mehr als 3 Bewegungsgesetze. Newton zeigt vielmehr wie man ausgehend von 3 expliziten Axiomen unter Anwendung der implizit als physikalisch legal gehandhabten mathematischen Operationen Superposition und Summation/Integration sehr viel erklären, ja sogar berechnen kann.
Schach-Reglement … o.k., passt weitestgehenst.
Aber es ist an den Extremen eben nicht so, dass da “Schluß” ist, weil die Regeln es so wollen. Quantenmechaisch scheint es keine Regeln mehr zu geben, wenn auf kleinster Ebene der Zufall wirkt – etwa bei der Entstehung neuer Elemente, vielleicht beim “noch schwereren Element”, welches bis jetzt noch nicht bekannt ist / es nicht gibt, ist die Regel scheinbar auch unzuständig. Durch solche “Erweiterungen” wird die Regel angepasst werden müssen.
Man sollte bei diesem Vergleich vielleicht auch eine historische Perspektive reinbringen. Kepler steht am Beginn der modernen Naturwissenschaften und seine Bahngesetze waren damals eine Revolution im Weltbild. Sein Puzzlebild ist also durchaus neu.Die Bahngesetze stehen im Kontext seiner ganzen Weltanschauung und seiner Idee einer Weltharmonik. Er hat eine nicht hinterfragbare Prämisse, nämlich dass der Kosmos nach harmonischen Verhältnissen strukturiert sein muss, eine Auffassung, die bei ihm religiös-philosophisch fundiert ist. Diese Harmonik wollte er mathematisch nachweisen.
Ja, Kepler, der exzellente Mathematiker und Vermesser des Himmels, war trotz kopernikanischem Gedankengut ein Harmoniker und kein Revolutionär. Er verbesserte das Wissen um die genauen Sternenpositionen um eine Grössenordnung (zusammen mit Brahe) und fand die Weltenharmonie in den elliptischen und auch sonst “schönen” Planetenbahnen. Doch er sah nicht hinter die Kullissen. Offenbar brauchts noch etwas anderes um ein guter Physiker zu sein als mathematische Begabung und den Hang zum präzisen Arbeiten – oder/und die Zeit war damals noch nicht reif für mehr.
Kepler an Newton zu messen, finde ich nicht ganz gerecht, Wissenschaft braucht auch ihre Zeit, sich zu entwickeln. Ein Vergleich mit Galileo wäre historisch angemessener. Was heißt es um 1600, ein “Physiker” zu sein? Diese Wissenschaft hat sich damals ja gerade erst entwickelt.
‘Physik ist wie ein Puzlle – nicht wie ein Schach’ ginge auch.
Es gibt denn auch Konzepte oder Theoretisierungen der Physiklehre, die nur in einem bestimmten Bereich (“Puzzle”) funktionieren.
Vgl. auch mit dieser kleinen NASA-Animation:
-> http://apod.nasa.gov/apod/ap120312.html
Die Physiklehre ist “Schach” und “Puzzle”. – Übrigens ist “Schach” (gemeint sind alle komplexen Spiele mit vollständiger Information) rein praktisch “wegen Komplexität” Puzzle, aber auch wegen des “Puzzle”-Charakters, das “Puzzle” hat denselben Charakter.
Es gibt auch Spiele mit unvollständiger Information:
-> http://en.wikipedia.org/wiki/Bayesian_game
Poker beispielsweise, hier gilt es dann (Mit-)Spieler in ihrem Verhalten zu beobachten, Tendenzen betreffend.
Die Physiklehre [1] ist insofern ein Bayesian Game.
HTH
Dr. W
[1] die moderne skeptizistische Naturwissenschaft ist hier gemeint, die eine Methode ist, die Methodenträger benötigt, die Veranstaltung ist
* ‘Physik ist wie ein Puzzle – nicht wie ein Schach’ ginge auch.
Markus Pössel schrieb (14. November 2014):
> […] Fragen nach der Methodik (woher wissen wir, was wir wissen?) anzusprechen.
> Newtons Gesetze sagen nur, welche Beschleunigungen sich aus der Wechselwirkung der Objekte (sei es durch Stoß oder durch längerreichweitige Kräfte wie Gravitation) ergeben.
Methodischer schiene es zu lehren, dass Newton die Messgröße “Masse” erfunden und dadurch definiert hat, dass ein “Punktobjekt der Masse \( M \)” zur “Beschleunigung” jedes anderen “Punktobjekts” mit
\( G~M / r^2 \)
beiträgt;
wobei \( r \) ein Maß des “(instantanen) Abstands” zwischen den beiden betrachteten “Punktobjekten” ist, und \( G \) eine geeignete dimensionsbehaftete formale Konstante.
Aus diesen Begriffen kann man jede Menge Modelle basteln; insbesondere je nach Annahme, ob und was außer den “Massen” noch zu den eventuellen “Beschleunigungen” der betrachteten Objekte beitragen würde.
Dass sich Newton aber nicht (oder kaum?) um die Methodik gekümmert hat, ob und wie zugrundeliegende “geometrische” Begriffe (“Beschleunigung”, “(instantaner) Abstand”) zumindest im Prinzip als Messgrößen definiert sein könnten, zeigt sich deutlich an der Fassung von “_Newtons Gesetzen_” nach Eddington:
> In Newtons Welt könnte das Sonnensystem auch ganz andere Abstandsverhältnisse aufweisen – allein Stabilitätsüberlegungen (ob sich Planeten bei einer bestimmten Abstandskonfiguration zu nahe kämen und sich aus dem Sonnensystem oder auf andere Bahnen lenken würden) schränken ein, was machbar ist.
Das hieße offenbar, “das Sonnensystem in Newtons Welt” auf Modelle einzuschränken, in denen nur “Massen” zu den (eventuellen) “Beschleunigungen” der betrachteten Objekte beitragen würde; oder sogar: nur die “Massen” dieser betrachteten Objekte selber, aber nicht z.B. die von eventuellen “Passanten”.
Die methodische Zurückweisung solcher Einschränkungen kann man so zusammenfassen:
Zustimmung in einem Punkt Herr Wappler: Newton wie auch seine Zeitgenossen haben gewisse Dinge vorausgesetzt und als selbstverständlich betrachtet, die es bei genauerem Hinsehen eben gar nicht sind.
Dazu gehört die Annahme, wir befänden uns in einem euklidischen Raum, was Newton als so selbstverständlich betrachtete, dass er dafür nicht die Physik sondern die Mathematik für zuständig ansah.
Auch die universale Gültigkeit des Gravitationsgesetzes, die Newton annahm obwohl er das Gesetz ja aus der Bewegung der Himmelskörper ableitete wird soviel ich weiss kaum diskutiert in seinem Werk. Und ja, was Masse ist, das sagt Newton ja eigentlich nur über die Formeln in denen Masse vorkommt. Damit defniert er eigentich was Masse ist. Daran habe ich nichts auszusetzen, das entspricht der axiomatischen Methode in der Mathematik. Nur hat er wenig darüber “philosophiert”, hat er das wenig problematisiert.
Martin Holzherr schrieb (17. November 2014 12:14):
> […] was Masse ist, das sagt Newton ja eigentlich nur über die Formeln in denen Masse vorkommt. Damit definiert er eigentich was Masse ist.
Sicherlich trägt nicht jede Formel Newtons, in der “Masse” vorkommt, zu deren Definition bei.
“Masse” kann ja auch als Grundlage weitergehender Definitionen dienen; insbesondere von “Kraft”
…
(Und ich möchte meinen vorausgegangenen Kommentar dahingehend ergänzen, dass Newton gewiss auch als zumindest einer der Erfinder dieser Messgröße Anerkennung verdient und erhält.)
> Newton wie auch seine Zeitgenossen haben gewisse Dinge vorausgesetzt und als selbstverständlich betrachtet, die es bei genauerem Hinsehen eben gar nicht sind.
Sofern “Dinge” nicht ausdrücklich benannt und mit Mitteln dargestellt hat, die man jedem (wie sich selbst) als selbstverständlich nachvollziehbar zugesteht, nennt man sie aber eher “ungewiss“.
Danke für Ihren Beitrag!
Ich denke allerdings eher, die Welt hat etwas mit einem Puzzle gemein. Abgesehen vom echten Zufall aus der Quantenwelt ist die Welt offenbar deterministisch. Auch das Fällen der Zufallsereignisse lässt, da eben zufällig, letztlich keinen Raum für Alternativen. Also gibt es für die ‘Weltkurve’ nur einen zwingenden Weg – wenn auch durch den Zufall aus der QM nur innerhalb gewisser Grenzen berechenbar. Lediglich abstrahierte Realisierungen von Teilaspekten der Welt (z.B. fallende Äpfel) haben genau einen Freiheitsgrad: Nämlich welche(n Apfel) man betrachtet. Reale Objekte besitzen keine Freiheit.