Neue Gerüchte zu Gravitationswellen-Nachweis: Was erwartet uns?
BLOG: RELATIV EINFACH

Dass zunächst die Gerüchte fliegen und wird dann später Gewissheit haben, war ja bereits bei der ersten Entdeckung von Gravitationswellen – lichtschnellen Raumverzerrungen, die sich wellenartig ausbreiten – so. Jetzt, etwas seit Mitte August, gibt es neue Gerüchte über einen ganz besonderen weiteren Gravitationswellennachweis – den der Verschmelzung von zwei Neutronensternen. Der zitierte Spektrum-Beitrag fasst gut zusammen, worum es geht; hier von meiner Seite nur einige Kommentare zu bestimmten Aspekten, die ich besonders interessant finde, sämtlich basierend auf Informationen, die frei zugänglich sind. Es gibt nämlich eine ganze Reihe von Gründen, warum der neue Nachweis potenziell besonders spannend ist. Also, sind in dieser unauffälligen elliptischen Galaxie…

…zwei Neutronensterne verschmolzen, und konnten die entsprechenden Gravitationswellen nachgewiesen werden?
Gut, dass es vorher immer Schwarze Löcher waren…
Bislang sind drei Gravitationswellen-Nachweise veröffentlicht: das vor rund einem Jahr gemessene allererste Signal Signal GW150914, das “Weihnachtssignal” GW151226 und das bislang letzte veröffentlichte Signal GW170104 vom 4. Januar dieses Jahres. Alle drei stammten von der Verschmelzung je zweier Schwarzer Löcher. Der Vorteil daran: Schwarze Löcher sind vergleichsweise einfach zu beschreiben und zu simulieren. An Physik geht dabei nicht mehr ein als Einsteins Gravitationstheorie, seine Allgemeine Relativitätstheorie. Für erste Nachweise sind solche überschaubar komplizierten Signale sehr günstig.
Und selbst da war es eine wichtige Bestätigung, dass die Computersimulationen auf Basis der Allgemeinen Relativitätstheorie die gemessenen Wellenformen so gut beschreiben. Gravitationswellen sind ja gerade deshalb so spannend, weil sie Informationen z.B. über die Regionen direkt an der Grenze zum Schwarzen Loch enthalten. Bei so starker Gravitation werden die Unterschiede zwischen Einsteins Theorie und der klassischen, newtonschen Gravitation besonders deutlich. Und in Bereichen so starker Gravitation hatte man die Simulationen eben vor dem Gravitationswellen-Nachweis eben noch nie an Beobachtungsdaten überprüfen können.
…und dass es jetzt Neutronensterne sind
Umso spannender ist es nun aber, dass es jetzt offenbar mit etwas ganz anderem weiter geht. Schwarze-Loch-Signale hatten wir jetzt verstanden. Bei dem gerüchteweisen Nachweis soll es sich nun aber um verschmelzende Neutronensterne handeln, jeder davon der Rest eines massereichen Sterns. Neutronenstern-Materie ist extrem dicht; ein Neutronenstern ist so etwas wie ein riesenhafter, ungeladener Atomkern dessen Querschnittsfläche ungefähr so groß ist wie eine Großstadt – für astronomische Verhältnisse also sehr, sehr klein. Ein Zuckerwürfel voll Neutronensternmaterie hätte die Masse eines größeren Bergs. (Aber einen Zuckerwürfel voll solcher Materie wird man nie alleine antreffen – nur die entsprechend große Masse erlaubt solch exotische Materiezustände.)
Wer verschmelzende Neutronensterne und deren Gravitationswellensignale verstehen will, muss deutlich mehr wissen als nur das, was die Allgemeine Relativitätstheorie sagt. Er muss auch Neutronenmaterie verstehen. Im Gegenzug heißt das: Gravitationswellen-Signale einer solchen Neutronensternverschmelzung würden uns zeigen, ob unsere Modelle für Neutronensterne richtig sind oder nicht. Und das ist viel wert.
Dass Einsteins Theorie durch die Schwarz-Loch-Verschmelzungs-Gravitationswellen-Signale bestätigt wurde, hat unter den Gravitationsphysikern so gut wie niemanden so richtig überrascht. Ob wir Neutronenmaterie verstehen, ist eine deutlich spannendere Frage. Einsteins Theorie ist mathematisch aus einem Guss. Da gibt es so gut wie keine Möglichkeiten, etwas zu verändern, ohne gleich die ganze Beschreibung der Gravitation radikal auf den Kopf zu stellen (und dabei aller Wahrscheinlichkeit bereits mit den bestehenden Tests der Theorie in Konflikt zu geraten).
Flexibilität macht den Nachweis interessant
Die Neutronenstern-Modelle sind deutlich flexibler. Und damit sind Tests, die zeigen, ob die vielen Annahmen, die in diese Modelle eingehen, zu richtigen Voraussagen führen, eben sehr interessant. Eine ganze Reihe von Daten liefern uns sogenannte Pulsare, also rotierende Neutronensterne, die wie kosmische Leuchttürme ihre Umgebung mit großer Regelmäßigkeit mit eng gebündelter Strahlung überstreichen. Aber eine ganze Reihe von Fragen sind noch offen.
Das betrifft so elementare Modell-Bausteine wie die sogenannte Zustandsgleichung, also der Zusammenhang zwischen Dichte und Druck der Neutronenmaterie. Im irdischen Labor lassen sich die entsprechenden extremen Bedingungen nicht nachstellen. Aber bei der Verschmelzung zweier Neutronensterne, und der dabei stattfindenden Aussendung von Gravitationswellen, spielt die Zustandsgleichung eine wichtige Rolle, und anhand der Gravitationswellensignale lassen sich Rückschlüsse zumindest auf einige Eigenschaften der Zustandsgleichung ziehen. Das wäre dann nicht nur eher langweiliges Einstein-Bestätigen, sondern richtige Gravitationswellen-Astronomie: Die Erforschung der Struktur und Eigenschaften von Himmelskörpern mithilfe von Gravitationswellen.
Ein wichtiger Ring
Die erste vollständige Computersimulation, die realistisch nachweisen konnte, wie Neutronenstern-Eigenschaften und die Gravitationswellensignale verschmelzender Neutronensterne zusammenhängen, stammt von Luca Baiotti, Bruno Giacomazzo und Luciano Rezzolla, damals alle mit dem Max-Planck-Institut für Gravitationsphysik (Albert-Einstein-Institut) in Potsdam affiliiert, und erschien 2008 im Physical Review. Ich hatte die schöne Gelegenheit mit Luciano einen entsprechenden Artikel für Sterne und Weltraum zu schreiben, der die Forschungsergebnisse zusammenfasst. Aus dem Artikel folgt nämlich nicht nur, das die Gravitationswellensignale tatsächlich von den Eigenschaften der Neutronensternmaterie abhängen, sondern noch etwas weiteres. Die folgenden Bilder zeigen, was bei der Verschmelzung passiert (Quelle: AEI-Pressemitteilung):
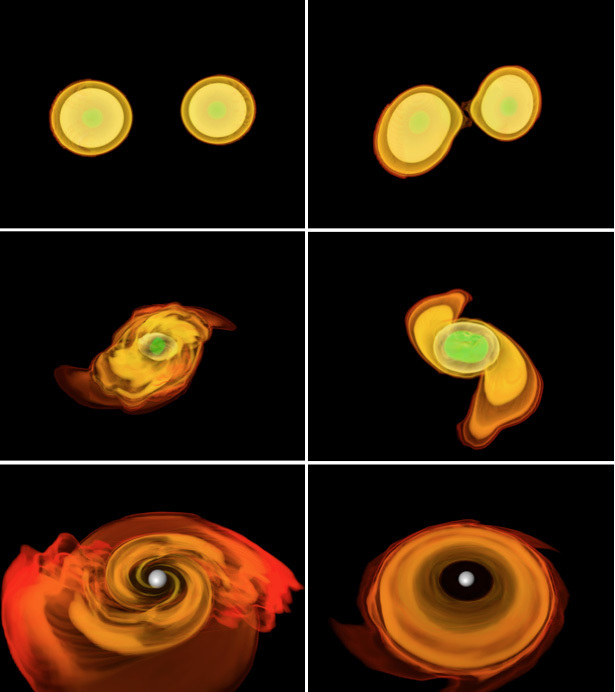
Neutronensterne haben eine gewisse Grenzmasse. Wenn zwei davon verschmolzen sind, wie im Bild Mitte rechts der Fall, ist zuviel Masse da, und der “hypermassereiche Neutronenstern” kollabiert binnen Sekundenbruchteilen zu einem Schwarzen Loch (graue Kugel in den unteren beiden Bildern). Das Schwarze Loch ist allerdings, das zeigen die Simulationen von Baiotti und Kollegen ganz eindeutig, noch von einem Ring von Neutronenmaterie umgeben. Und das ist sehr, sehr, wichtig. Auf solch ein Ergebnis hatten die Astronomen nämlich sehnlichst gewartet.
Gammablitze
Gammablitze wurden Ende der 1960er Jahre von Satelliten entdeckt, die eigentlich die Spuren von Kernwaffenexplosionen nachweisen sollten. Über die Jahre hinweg fand man immer mehr solcher Blitze, und das Puzzle wurde vollständiger: Die Ereignisse, die Gammablitze erzeugen, sind so weit weg wie sonst fast kein astronomisches Objekt. Entsprechend hell müssen die Blitze sein, um sich mit unseren Weltraumteleskopen so eindeutig nachweisen zu lassen. Der Dauer nach lassen sich lange und kurze Gammablitze unterscheiden: kurze mit weniger als zwei Sekunde dauer, lange mit im Mittel etwas mehr als einer halben Minute Dauer.
Mit der Zeit wuchsen auch die Hinweise darauf, welche Ereignisse hinter den Gammablitzen stehen. Für die langen Gammablitze sind demnach mit einiger Wahrscheinlichkeit die großen Brüder einer Supernova-Explosion verantwortlich. Als Supernova explodieren massereiche Sterne, wenn sie ihren Kernbrennstoff verbraucht haben. Die massereichsten Sterne, mit mehr als rund 25 Mal der Sonnenmasse, explodieren als entsprechend stärkere Hypernova, und solche Hypernovae scheinen für die länger dauernden Gammablitze verantwortlich zu sein (siehe diese ESO-Pressemitteilung von 2003).
Kurze Gammablitze
Die kürzeren Gammablitze sind etwas rätselhafter. Ihr Mechanismus scheint ein deutlich anderer als bei den Hypernovae (zeigen z.B. diese Beobachtungen von 2005). Die derzeit wahrscheinlichste Erklärung ist, dass es sich um verschmelzende Neutronensterne handelt – und an der Stelle kommt jetzt alles zusammen: Die Existenz eines Rings wie in den Simulationen von Baiotti et al. hatten die Astronomen sich erhofft, weil sich dadurch die Entstehung der hochenergetischen Strahlung erklären lässt: durch extrem hohe Temperaturen in der Ringmaterie entstehen Teilchen-Antiteilchenpaare; die Neutrinos und Antineutrinos, die dabei enstehen, zeigen (neutrinotypisch!) kaum Wechselwirkung mit der Ringmaterie und entkommen. Eine genügend hohe Anzahl dieser Neutrinos und Antineutrinos vernichten sich außerhalb des Rings, und dabei entsteht die hochenergetische Strahlung. Die Simulation von Baiotta und Kollegen zeigt, dass dieser Verlauf bei Neutronensternverschmelzungen die Regel ist und nicht die Ausnahme – gute Nachrichten für all jene, die hoffen, auf diese Weise die kurzen Gammablitze zu erklären.
Der direkte Nachweis von Gravitationswellen verschmelzender Neutronensterne und die gleichzeitige Beobachtung eines Gammablitzes würden klare Verhältnisse schaffen und zeigen: ja, verschmelzende Neutronensterne stecken in der Tat hinter den kurzen Gammablitzen.
Alle schauen auf ein Ereignis
Allein der Umstand, dass man in solch einem Fall beides zusammen hätte, Gravitationswellen und elektromagnetische Strahlung, wäre bereits sehr spannend. Zum einen hätte man damit eben wirklich vielfältige Informationen über ein und dasselbe Ereignis, die sich hervorragend ergänzen würden – viele schöne Daten, um die bestehenden Modelle kritisch auf die Probe zu stellen.
Zweitens sind vielfältige Beobachtungen günstig, um die Gerüchte zu konkretisieren. Nicht, weil damit viel mehr weitere Astronomen beteiligt wären und irgendwann jemand nicht mehr dichthält, sondern weil viele der entsprechenden Observatoriumsdaten öffentlich sind. In dem Spektrum- bzw. Nature-Artikel wird deswegen ja auch ganz direkt gesagt, um welchen Gammablitz es sich vermutlich handelt.
Aber schauen wir mal selbst nach: investigativer Wissenschafts-Datenjournalismus! Es soll um den 17. August 2017 gehen. Laut der Trigger-Liste des Fermi-Teleskops, die hier online ist, gab es kurz nach 12:41 UT eine ganze Reihe von Triggern. Trigger, das heißt: ein möglicher Gammablitz-Kandidat, den der Satellit dann tunlichst gleich untersuchen sollte:
 Der letzte davon stammt vom Fermi-Satelliten selbst. Der hat einen “Gamma Burst Monitor”, der den gesamten gerade sichtbaren Himmel absucht, alles was nicht von der Erde verdeckt ist, kontinuierlich im Blick hat und mitbekommt, wenn irgendwo ein Gammablitz anfängt. Bei einigermaßen vielversprechenden Kandidaten wird das Satellitenteleskop dann sofort auf das neue Ziel ausgerichtet und beobachtet. Die ersten vier Trigger waren “ground-generated”; für mich sieht das nach Kandidaten aus, die von anderen Observatorien an Fermi gemeldet wurden (auch wenn ich dann nicht ganz erklären kann, warum sie exakt in derselben Hundertstelsekunde ankamen). Die Details kann man später immer noch klären. Jedenfalls ist da etwas passiert.
Der letzte davon stammt vom Fermi-Satelliten selbst. Der hat einen “Gamma Burst Monitor”, der den gesamten gerade sichtbaren Himmel absucht, alles was nicht von der Erde verdeckt ist, kontinuierlich im Blick hat und mitbekommt, wenn irgendwo ein Gammablitz anfängt. Bei einigermaßen vielversprechenden Kandidaten wird das Satellitenteleskop dann sofort auf das neue Ziel ausgerichtet und beobachtet. Die ersten vier Trigger waren “ground-generated”; für mich sieht das nach Kandidaten aus, die von anderen Observatorien an Fermi gemeldet wurden (auch wenn ich dann nicht ganz erklären kann, warum sie exakt in derselben Hundertstelsekunde ankamen). Die Details kann man später immer noch klären. Jedenfalls ist da etwas passiert.
Auch der ESA-Gammastrahlensatellit INTEGRAL hat den Ausbruch zu genau derselben Zeit nachgewiesen.
Auch die ESO-Teleskope schauen hin
Die Observatorien der ESO in Chile sind zu dem Zeitpunkt noch nicht involviert. Das ändert sich am 18. August: sobald es in Chile dunkel wird, bietet sich ein ungewöhnliches Schauspiel. Teleskopzeit wird typischerweise auf Antrag vergeben, und ist ein knappes Gut – die ESO-Teleskope sind in jeder Antragsperiode weit überbucht. Jede Beobachtung bekommt die minimale Zeit, die nötig ist, um das wissenschaftliche Ziel zu erreichen. Entsprechend vielfältig sind die Ziele, die etwa von den Teleskopen an den beiden ESO-Observatorien Paranal und La Silla in einer Beobachtungsnacht angepeilt werden. Nicht so in der Nacht des 18. August. Schaut man sich für diesen Zeitraum die im ESO Science Archive verfügbare Metadaten für die einzelnen Teleskope an, dann findet man seltene Eintracht: Gleich drei der vier VLT-Hauptteleskope am Paranal-Observatorium, jedes davon mit einem 8-Meter-Spiegel, sind auf den gleichen Punkt am Himmel gerichtet; ebenso das New Technology Telescope und das 2.2m MPG/ESO-Teleskop auf La Silla.
Das FORS2-Instrument UT1 sagt auch, was es beobachtet:
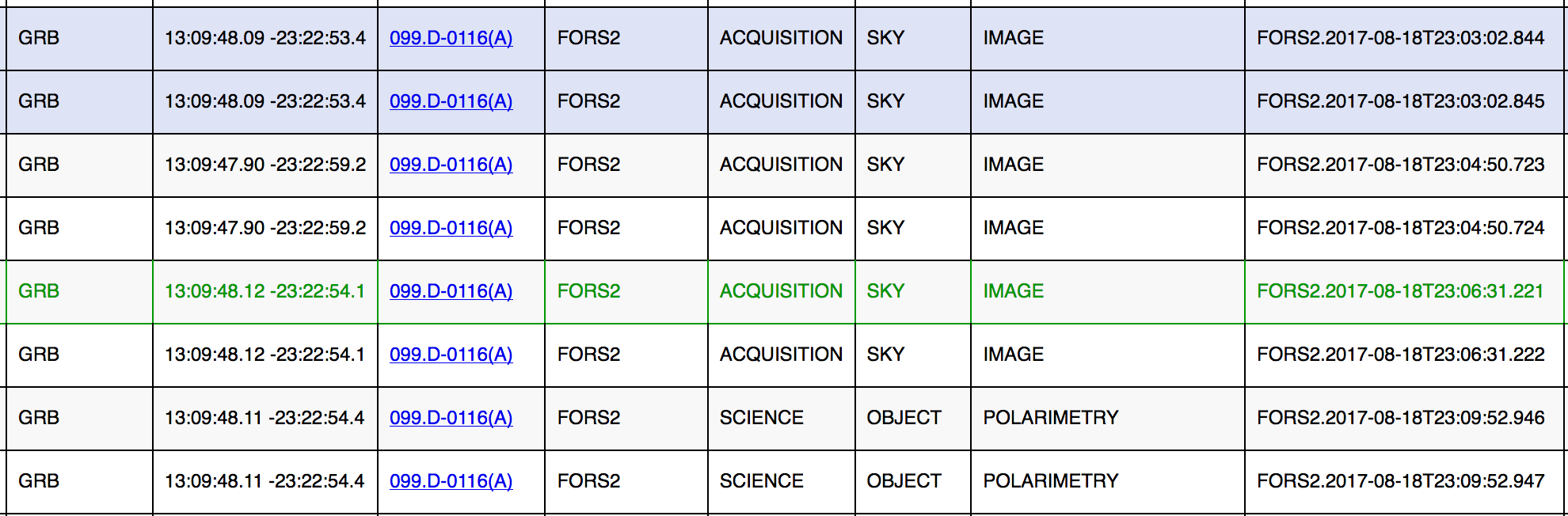 Einen GRB, also einen Gamma Ray Burst. Und bei den angegebenen Daten, 13:09:48.11 und -23:22:54.4 finden wir eben die angegebene unauffällige elliptische Galaxie:
Einen GRB, also einen Gamma Ray Burst. Und bei den angegebenen Daten, 13:09:48.11 und -23:22:54.4 finden wir eben die angegebene unauffällige elliptische Galaxie:

Just ein paar Tage später schaut auch das Hubble Space Telescope ein paar Mal auf diese Galaxie:
 Angegeben sind dabei Hilfsbilder, die zur Kalibration aufgenommen wurden. Ob die Wissenschaftsbilder erst später aufgelistet werden, wenn sie im Archiv eingestellt werden, weiß ich nicht genau. Jedenfalls läuft auch beim Hubble etwas in diesem Zielbereich.
Angegeben sind dabei Hilfsbilder, die zur Kalibration aufgenommen wurden. Ob die Wissenschaftsbilder erst später aufgelistet werden, wenn sie im Archiv eingestellt werden, weiß ich nicht genau. Jedenfalls läuft auch beim Hubble etwas in diesem Zielbereich.
Gegenseitige Kontrolle
Ich will an dieser Stelle gar nicht zu sehr in die Details gehen. Wir werden früher oder später erfahren, was dort die Aufmerksamkeit der verschiedenen Teleskope gefesselt hat, und ob es etwas mit Gravitationswellen zu tun hatte.
Wenn zusammengehörige Beobachtungen gelungen sind, Gravitationswellen hier, elektromagnetische Teleskope dort, deren Verlauf zu ein und demselben Ereignis passt, ist das jedenfalls ein weiterer grundlegender Schritt. Natürlich haben die LIGO-Betreiber aufwändige Studien betrieben, um die Eigenschaften ihres Detektor-Rauschens zu verstehen und mit überwältigender Wahrscheinlichkeit ausschließen zu können, dass sie Rauschen und Signal verwechseln. Aber eine komplett unabhängige Bestätigung, mit herkömmlichen Teleskopen, die auf ganz anderen Prinzipien basieren als Gravitationswellendetektoren, ist noch einmal eine ganz andere Ebene der Bestätigung.
Wobei man einen weiteren Umstand nicht vergessen darf: In dem Zeitraum, in dem es geht, war auch Virgo am Start, der italienisch-französische Detektor in der Nähe von Pisa (hier mein Bericht von einem Besuch bei Virgo). Virgo und die beiden LIGO-Detektoren haben vom 1. bis zum 25. August 2017 gemeinsam nach Gravitationswellen gelauscht. Bereits ein gemeinsam von den beiden LIGOs und dem in einiger Hinsicht anders konstruierten Virgo wäre eine unabhängige Bestätigung, dass alle drei Detektoren tatsächlich Gravitationswellensignale messen.
Kosmologie und Entfernungsleiter
Ich persönlich finde am spannendsten, was sich aus dem Nachweis verschmelzender Neutronensterne für die Kosmologie ergibt. Noch nicht so sehr aus einem, aber aus einer genügend großen Menge davon. Die sogenannte Hubble-Relation besagt, dass in einem expandierenden Universum die Rotverschiebung einer fernen Galaxie und die Entfernung der Galaxie zu uns direkt zusammenhängt, verkürzt gesagt: je weiter entfernt die Galaxie, desto rascher entfernt sie sich aufgrund der kosmischen Expansion von uns. Diese Relation ist freilich gar nicht so einfach zu testen. Entfernungsbestimmungen sind in der Astronomie grundlegend schwierig, und um die Entfernungen zu Galaxien zu messen, sind bereits mindestens vier verschiedene Methoden nötig, deren eine auf die nächste aufbaut (sogenannte “kosmische Entfernungsleiter”).
Verschmelzende Neutronensterne oder Schwarze Löcher sind in der Hinsicht ganz anders. Direkt aus dem Gravitationswellensignal lassen sich ziemlich genaue Rückschlüsse darauf ziehen, in welcher Entfernung von uns die Verschmelzung stattgefunden hat. Das nützt für sich allein genommen noch nichts, denn für die Hubble-Relation benötigt man außer der Entfernung eben noch die Rotverschiebung, und die ist einem solchen Gravitationswellensignal ausgerechnet nicht anzusehen. Ganz anders, wenn man dasselbe Ereignis auch im elektromagnetischen Bereich beobachtet und die Heimatgalaxie des Signals identifiziert hat.
Das expandierende Universum überprüfen
Die Rotverschiebung einer Galaxie ist in der Regel gut zu bestimmen. Auf diese Weise ließe sich die Hubble-Relation ganz unabhängig von der üblichen kosmischen Entferungsleiter überprüfen; das hat zuerst der Ex-Direktor meines ehemaligen Instituts, Bernard Schutz, bemerkt und 1986 veröffentlicht. Mit 10 solchen Ereignissen bis hinaus zu einer Entfernung von 100 Mpc, so seine Abschätzung, ließe sich die sogenannte Hubble-Konstante, welche die derzeitige Ausdehnungsrate des Universums beschreibt, mit einer Genauigkeit von 3% bestimmen.
Das wäre gerade zum jetzigen Zeitpunkt sehr interessant für die Kosmologen. Derzeit sind leicht unterschiedliche Werte für die Hubble-Konstante: ein etwas geringerer Wert, bestimmt aus Messungen der kosmischen Hintergrundstrahlung und damit weitgehend aus Eigenschaften des sehr frühen Universums (Planck Consortium 2016), und ein etwas größerer Wert, bestimmt durch Messungen an Supernovae vom Typ Ia (Riess et al. 2016). Das folgende Diagramm zeigt die Linien auf denen die Galaxien-Datenpunkte, jeder davon definiert durch Abstand (x-Wert) und Fluchtgeschwindigkeit (y-Wert) der Galaxie, laut Planck bzw. Riess zu liegen kommen sollten, außerdem die derzeit beste Schätzung für die Position von NGC 4993:
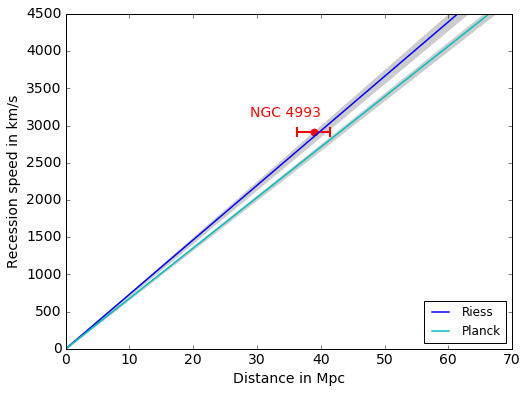 Wenn in NGC 4993 tatsächlich eine Neutronensternverschmelzung nachgewiesen wurde und wenn, auch das ist ja nicht klar, diese Verschmelzung tatsächlich in NGC 4993 (und nicht von uns aus gesehen davor oder dahinter) stattgefunden hat, dann wird es möglich sein, den Datenpunkt in diesem Diagramm genauer zu positionieren. Danach ja hoffentlich noch weitere Datenpunkte, und mit ihnen unabhängige Nachweise dafür, welche der beiden Messungen, Riess oder Planck, unser lokales Universum am besten beschreibt. Spannend ist natürlich, ob die Diskrepanz auf systematischen Fehlern beruht – die werden in der Wissenschaft ja gerne einmal unterschätzt – oder ob sie anzeigt, dass sich das Weltall doch etwas anders verhält, als es unsere Modelle vorhersagen.
Wenn in NGC 4993 tatsächlich eine Neutronensternverschmelzung nachgewiesen wurde und wenn, auch das ist ja nicht klar, diese Verschmelzung tatsächlich in NGC 4993 (und nicht von uns aus gesehen davor oder dahinter) stattgefunden hat, dann wird es möglich sein, den Datenpunkt in diesem Diagramm genauer zu positionieren. Danach ja hoffentlich noch weitere Datenpunkte, und mit ihnen unabhängige Nachweise dafür, welche der beiden Messungen, Riess oder Planck, unser lokales Universum am besten beschreibt. Spannend ist natürlich, ob die Diskrepanz auf systematischen Fehlern beruht – die werden in der Wissenschaft ja gerne einmal unterschätzt – oder ob sie anzeigt, dass sich das Weltall doch etwas anders verhält, als es unsere Modelle vorhersagen.
Fazit
Das Gerücht ist derzeit ein Gerücht. Genaueres wissen wir dann, wenn die LIGO- und Virgo-Wissenschaftler es bekanntgeben – und das dürfte wieder geschehen, wenn der entsprechende Fachartikel zur Veröffentlichung akzeptiert ist. Bis dahin ist es sicher nicht falsch, sich zu vergegenwärtigen, was es mit einer solchen Entdeckung auf sich hätte: Neue Informationen über Neutronensterne, eine Bestätigung (oder eben nicht) des vielversprechendsten Modells für Gammablitze, ein erstes Beispiel für Gravitationswellenastronomie im Zusammenspiel mit herkömmlichen astronomischen Beobachtungen, dadurch und durch das gemeinsame Beobachten mit Virgo eine noch deutlich größere Sicherheit, dass die Gravitationswellendetektoren tatsächlich so funktionieren wie angenommen, und nicht zuletzt der Auftakt zu interessanten Aussagen über die Expansion unseres Weltalls.
Das wäre ein gehöriger Strauß an Erkenntnissen. Nicht ganz in derselben Klasse wie der erste direkte Nachweis von Gravitationswellen, aber ganz sicher ein Meilenstein. All das sollten wir im Hinterkopf behalten, und uns dann gedulden – die LIGO- und Virgo-Wissenschaftler sollten sich jetzt soviel Zeit nehmen, wie sie brauchen, um eine sorgfältige Analyse vorzunehmen. Und dann werden wir hoffentlich wieder deutlich mehr über unser Universum wissen.


Markus Pössel schrieb (19. September 2017):
> Bislang sind drei Gravitationswellen-Nachweise veröffentlicht: das vor rund einem Jahr gemessene allererste Signal Signal GW150914, das “Weihnachtssignal” GW151226 und das bislang letzte veröffentlichte Signal GW170104 vom 4. Januar dieses Jahres. Alle drei stammten von der Verschmelzung je zweier Schwarzer Löcher.
Diese drei Signale wurden mit ziemlicher Sicherheit von Verschmelzungen je zweier Schwarzer Löcher verursacht.
Aber um (die Ausbreitung von) Gravitationswellen im Sinne der Allgemeinen Relativitätstheorie zweifelsfrei nachzuweisen, ist zu verlangen, dass die Krümmung von Raumzeit gemessen und ggf. deren periodische Veränderung (in der Detektor-Region) gefunden würde.
(Sofern die erforderlichen Messungen der Raumzeit-Krümmung bisher noch nicht erfolgten, mag ja von “Hinweisen auf Gravitationswellen” gesprochen werden.)
> Schwarze Löcher sind vergleichsweise einfach zu beschreiben und zu simulieren. […] da war es eine wichtige Bestätigung, dass die Computersimulationen auf Basis der Allgemeinen Relativitätstheorie die gemessenen Wellenformen so gut beschreiben.
So weit, so gut.
> Dass Einsteins Theorie durch die Schwarz-Loch-Verschmelzungs-Gravitationswellen-Signale bestätigt wurde […]
Nein:
das Auffinden von Wellenformen, die den simulierten gut gleichen, bestätigt (bzw. korroboriert) das simulierte Modell; nämlich, dass “Verschmelzungen je zweier Schwarzer Löcher” tatsächlich (und sogar geeignet häufig) vorgekommen sind.
Die Theorie dagegen, durch die Begriffe wie “Schwarzes Loch” und “Verschmelzen” (und natürlich auch “Gravitationswelle“) und die damit verbundenen Messgrößen (insbesondere “Krümmung der Raumzeit”, “Entfernung” usw.) überhaupt erst definiert sind,
bedarf keiner Bestätigung und lässt sich experimentell weder bestätigen noch widerlegen.
Klar sind bei Tests immer sowohl die Theorie und ein spezifisches auf dieser Theorie basierendes Modell im Spiel – dazu hatte ich ja auf diesem Blog auch vor längerem einiges geschrieben, angefangen hier. Die Aussage
“lässt sich experimentell weder bestätigen noch widerlegen” ist aber so, wie sie die allermeisten Leser Ihres Kommentars verstehen dürften, falsch. Selbstverständlich fallen Misserfolge bei experimentellen Prüfungen auch auf die zugrundeliegende Theorie zurück. Sicher nicht automatisch, absolut und direkt, aber hinreichend viele Misserfolge bei Modellen, die wenig Spielraum lassen, den Misserfolg von der zugrundeliegenden Theorie auf das spezifische Modell zu schieben, führen dazu, dass die betreffende Theorie dann eben widerlegt ist und fallengelassen wird. Widerlegt nicht im mathematischen Sinne (wir sind ja hier nicht in der reinen Mathematik), aber in einem durchaus wichtigen praktischen Sinne.
Markus Pössel schrieb (22. September 2017 @ 09:22):
> […] dazu hatte ich ja auf diesem Blog auch vor längerem einiges geschrieben, angefangen hier.
Und ich hatte dazu einiges zu erwidern; vorerst bis da hin
(soweit ich dort erkenne, und mich erinnern kann. Aber es gibt ja recht häufig neue Anlässe, dieses Thema anzupacken; also danke für die Kenntnisnahme meiner erneuten diesbezüglichen Bemühungen).
Beim Überfliegen der Kommentare auf der verlinkten alten SciLogs-Seite ist mir ein Kommentar (25. Januar 2014 @ 16:57) von Martin Holzherr (ausgerechnet! ;) aufgefallen, anhand dessen sich meine Auffassung zu “unser Thema” auf den Punkt bringen lässt. Dort schrieb er nämlich:
Wenn das eben so ist … wie nennt man dann zur Unterscheidung ein
“System wissenschaftlich begründeter Aussagen zur Feststellung von Tatsachen.”
??
Warum kein Wort zur jetzt (sehr wahrscheinlich) endlich möglichen experimentellen Klärung, ob Gravitationswellen wirklich Tensorwellen sind, wie dies Einsteins Allgemeine Relativitätstheorie verlangt oder vielleicht doch Vektorwellen, wie dies Heaviside schon 1893 vorhersagte? Klarheitshalber: Für diese Überprüfung braucht man nichts über die Quelle der Wellen zu wissen ausser ihre Position am Himmel. Oder sollten folgende zwei Sätze Pössels Ansicht dazu wiedergeben, nämlich letztlich, dass dieser Test uninteressant sei, weil Gravitationswellen ja ohnehin nur Tensor- bzw. Einsteinwellen sein könnten:
„Einsteins Theorie ist mathematisch aus einem Guss. Da gibt es so gut wie keine Möglichkeiten, etwas zu verändern, ohne gleich die ganze Beschreibung der Gravitation radikal auf den Kopf zu stellen (und dabei aller Wahrscheinlichkeit [nach] bereits mit den bestehenden Tests der Theorie in Konflikt zu geraten).“
Die Aussage Pössels in der Klammer ist nach heutigem Wissensstand für die Neuklassische Gravitation (NKG) falsch: Das sieht man in meinem Netzfenster http://www.wolff.ch/astro im ersten Teil „Aktueller Stand“ zusammengefasst in der einzigen Tabelle, die es auf der ganzen Seite gibt; diese Zusammenfassung ist allerdings so kompakt, dass sie wohl nur Sachkenner (sofort) verstehen können. Am Ende des ersten Teils gehe ich auch noch ganz kurz auf die Art der (NKG-)Gravitationswellen und die neuen Überprüfungsmöchlichkeit mit LIGO/VIRGO ein, ohne mich auf irgendwelche nicht öffentlich zugängliche Informationen zu beziehen, über die ich ohnehin nicht verfüge. Die Gerüchte liessen mich aber erstmals die neue Testmöglichkeit der ART erkennen; siehe:
http://www.wolff.ch/astro/LIGO-VIRGO-Kommentar.pdf
Ich habe versucht wiederzugeben, was in der wissenschaftlichen Community in Bezug auf die betreffenden Gerüchte wichtig ist. Was das für Ihre Privattheorie bedeutet, ist dafür nicht wirklich relevant – verständlich, dass Sie das anders sehen, aber so ist es.
»Schwarze Löcher sind vergleichsweise einfach zu beschreiben und zu simulieren. An Physik geht dabei nicht mehr ein als Einsteins Gravitationstheorie, seine Allgemeine Relativitätstheorie.«
Ist das wirklich so?
Für einen terrestrischen Beobachter müsste eine unendliche Zeitspanne vergehen, bis bei einem stellaren Kollaps ein Horizont entstehen könnte. Andreas Müller hatte sich hierzu verschiedentlich der Formulierung bedient, die Horizonte Schwarzer Löcher befänden sich in unserer Zukunft. Für meinen Geschmack tönt das ein wenig missverständlich, doch worauf es mutmasslich hinauslaufen soll ist, dass keine solchen Horizonte in der kausalen Vergangenheit eines terrestrischen Beobachters liegen. Womit er unzweifelhaft recht hätte. (Und vielleicht lässt er sich ja noch zu einem Statement bewegen, ob es denn so gemeint war.)
Wenn unser terrestrischer Beobachter nun eine Kollision zweier Kollapsare observationell bemerkt, so ist dies ein in seiner kausalen Vergangenheit liegendes Ereignis. Und für das, was er dabei beobachten könnte, sind Horizonte dann absolut ohne Belang, denn die hätten sich zum betreffenden Zeitpunkt noch gar nicht formiert.
Falls das bei einer solchen Kollision zu Beobachtende numerisch simuliert werden soll, ist demzufolge auch das Innere der beteiligten Sterne einzukalkulieren, nicht anders als bei kollodierenden Neutronensternen. Da jedoch niemand verlässlich sagen kann, wie sich Materie bei Dichten von mehr als ~10^{15} g/cm³ tatsächlich verhält, ist eine solide Grundlage für realistische Modellsimulationen eines solchen Szenarios gar nicht gegeben.
Ob numerisch oder schlechthin — die stellaren Black Holes sind eigentlich nur dann vergleichsweise einfache Objekte, wenn man es sich damit zu einfach macht. Was dann bekanntlich heisst, man macht es falsch.
Jein. Was ich sagen wollte, ist hoffentlich klar: Bei der Beschreibung dessen, was in die Simulation eingehen soll, gibt es bei Schwarzen Löchern klare Vorgaben (ART!) und bei Neutronensternen mehr Flexibilität, freie Parameter und Unsicherheiten z.B. bezüglich der Zusatzgleichungen.
Was Andreas Müller sagt, dürfte sich in der Tat auf die Lichtkegelstruktur beziehen – im Penrose-Diagramm sieht man da ja sehr schön, wie die kausale Struktur ist.
In numerischen Simulationen wählt man typischerweise Koordinaten, die bis in den Horizont hineinreichen; wo der Horizont liegt ergibt sich dann indirekt durch die Werte der Metrik während der Simulation. Dass es dabei immer kleine Rundungsfehler gibt, die dafür sorgen, dass doch ein paar Informationen über das Innere nach außen wandern, dürfte die Kernschwierigkeit bei der Simulation realistischer, verschmelzender Schwarzer Löcher sein. (In diesem Sinne sind solche Simulationen in der Tat nicht einfach; nur von den klar definierten Voraussetzungen her.)
Zur Argumentation mit den Gravitationswellen: Da, wo es nur um Licht und Gravitationswellen geht, die sich jeweils lichtschnell fortpflanzen, ist alle Information über den eigentlichen Kollaps der zwei Schwarzen Löcher, um die es geht, schon längst am irdischen Beobachter vorbeigelaufen. Dass sich vorher bereits Horizonte gebildet hatten (und damit keine weitere lichtschnelle Information aus dem Horizontinneren ankommt) ist damit ganz entscheidend dafür, dass die Vereinfachung durchaus legitim ist.
/Frage/ Der terrestrische Beobachter ist doch kein “unendlicher” Beobachter, sitzt auf einer Schale.
Demzufolge müßten für ihn zB nach 1,3 Mrd Jahren die verschmelzenden Horizonte da sein,
die hatten sich nach Koordinatenzeit doch vor ca. 5 Mrd Jahren gebildet.
Chrys schrieb (20. September 2017 @ 23:13):
> […] die stellaren Black Holes sind eigentlich nur dann vergleichsweise einfache Objekte, wenn man es sich damit zu einfach macht.
Dass mit “Black holes” (ob stellaren oder anderen Ursprungs) eigentlich doch vergleichsweise einfache Objekte gemeint sind, kommt u.a. auch im sogenannten “no-hair theorem” zum Ausdruck.
Aber einfach anzunehmen, dass alle ehemaligen Sterne, um deren gesamte (sichtbare, kompakte) Materie sich schon längst eine Photonsphäre ausgebildet hat, deswegen nie mehr (insbesondere) nicht-gravitativ agieren/ausbrechen oder reagieren bzw. sich anregen lassen könnten …
… (sondern stattdessen eben einfach genau solche oben gemeinten Black holes bleiben bzw. werden würden) …
… lädt zu Überraschungen ein.
Zitat Chrys:
Warum denn das? Wenn schon müsste für ein Teilchen gerade beim Horizont eine unendliche Zeit verstreichen bis es verschluckt ist, nicht aber für einen externen Beobachter. Oder bin ich da falsch gewickelt?
Nee, der Teil ist schon so wie Chrys es sagt. Für einen weit entfernten Beobachter sind die Abläufe in Horizontnähe, rekonstruiert aus den Lichtsignalen, die solch einen Beobachter erreichen, immer langsamer ab, je näher sie dem Horizont sind.
Markus Pössel schrieb (21. September 2017 @ 16:46):
> Für einen weit entfernten Beobachter sind die Abläufe in Horizontnähe, rekonstruiert aus den Lichtsignalen, die solch einen Beobachter erreichen, immer langsamer ab, je näher sie dem Horizont sind.
Und soetwas nach all der SciLogs-Kommentar-Korrespondenz, die von derart unsäglich schwammigen Formulierungen schon ausgelöst wurde; letztens dort beginnend! …
Wenigstens lässt sich dem hiermit (mal wieder) eine Formulierung entgegenstellen, die ich für nachvollziehbar und deshalb für vertretbar halte:
D.h. kurz (und zitierbar):
Ich versuche, von der potenziellen Leserschaft dieses Blogs (die natürlich ihrerseits nur einen vorselektierten Ausschnitt der Allgemeinbevölkerung darstellt) möglichst viele Leser weitgehend mitzunehmen. Sie schreiben Ihre Kommentare, Präzisierungen etc. als ginge es um ein Fachpublikum, oder potenzielles Fachpublikum. Auch von dem Anspruch her, dass ich durchaus damit rechne, dass hier Leser vorbeikommen, die weder tief in der Materie stecken noch meine vorigen Blogartikel (von denen ja einige systematischer versuchen, Wissen und Verständnis zu vermitteln) gelesen haben.
Für die allermeisten Leser dieses Blogs, so meine Einschätzung, sind die zwei Absätze, die Sie da schreiben, wirklich mühsam zu lesen und nur mit viel Anstrengung und vermutlich auch weiteren Nachforschungen nachvollziehbar. Klar, kann man machen. Gibt für die Leser, die es wirklich genau wissen wollen und sich systematisch einarbeiten, einen Mehrwert. Aber wenn ich in meinem Blog weitgehend so schreiben würde, wären die meisten potenziellen Leser außen vor. Kompromisse zwischen exakter (dann ja fast schon mathematischer) Sprache und leichter Verständlichkeit gehören in meinem Texten daher dazu – auch wenn ich wo irgend möglich versuche, beides unter einen Hut zu bringen.
Martin Holzherr schrieb (21. September 2017 @ 15:53):
> […] Oder bin ich da falsch gewickelt?
Ohne Chrys diesbezüglich vorzugreifen:
wohl (auch) ein wenig vergesslich, oder vielleicht “hinterm Berg”.
@all / Zum stellaren Kollaps
Vereinfachend lässt sich ein stationärer Beobachter im Schwarzschild Feld denken, der einen kollabierenden “Staubstern” beobachtet (d.i. Oppenheimer-Snyder Kollaps). Wenngleich nur ein reichlich simples Toy Model, ist es jedoch exakt berechenbar und daher illustrierend.
Dieser Beobachter beziehe sich für seine Observationen auf die mit seiner eigenen Uhr gemessene Zeit t als Zeitkoordinate; die ist proportional zur standard Schwarzschild-Zeit. Damit kann er den (Koordinaten-)Radius R(t) des Sterns zu einer beliebigen Zeit t bestimmen und findet, dass stets R(t) > R* nebst R(t) → R* asymptotisch für t → +∞ gilt, wobei R* den Schwarzschild-Radius der Sternmasse bezeichne. Idealerweise lebt der Beobachter ewig, dennoch erlebt er nicht die Entstehung eines Horizontes, sondern beobachtet einen ewig fortdauernden Kollaps des Sterns. Die Formulierung von Andreas Müller aufgreifend liesse sich dann sogar verschärfend sagen, dass der Horizont in der unendlich entfernten Zukunft dieses Beobachters liegt.
Im Unterschied dazu vergeht für eine auf der Oberfläche des kollabierenden Sterns befindliche Uhr eine endliche Zeitspanne, bis R* erreicht wird. Es mag erstaunen, ist aber keineswegs paradox, wenn bei zwei gleich rasch gehenden Uhren die erste nur eine endliche Zeitspanne misst, während dabei für die zweite gleichzeitig(!) unendlich viel Zeit verrinnt.
Genau, wobei man noch ergänzen sollte: dadurch, dass Licht von der kollabierenden Oberfläche beim Kollaps dann recht bald erheblich rotverschoben wird, entsteht für den äußeren Beobachter praktisch doch ein komplett schwarzes Gebilde; kein realer Beobachter (mit Detektoren endlich großer Empfindlichkeit) beobachtet einen unendlich fortdauernden Kollaps. Für die astrophysikalischen Überlegungen, was man (an Licht, Gravitationswellen, Gravitationseinfluss etc.) bei Schwarzen Löchern aus der Ferne nachweisen kann, ist diese Frage daher nicht von Belang.
Chrys schrieb (22. September 2017 @ 10:02):
> Vereinfachend lässt sich ein stationärer Beobachter im Schwarzschild Feld denken, der einen kollabierenden “Staubstern” beobachtet (d.i. Oppenheimer-Snyder Kollaps). […]
Das bedeutet wohl auch, dass dieser stationäre Beobachter von vornherein außerhalb (oder höchstens “zu Versuchsbeginn auf”) der Stauboberfläche war und blieb.
> Dieser Beobachter beziehe sich für seine Observationen auf die mit seiner eigenen Uhr
… einer seiner guten Uhren? …
> gemessene Zeit t als Zeitkoordinate; die ist proportional zur standard Schwarzschild-Zeit.
… Demnach offenbar: Ja, eine seiner guten Uhren; d.h. die ihren Anzeigen entlang ihres stationären Pfades so (“gleichmäßig”, und insbesondere: monoton wachsend) mit Werten t bestreußelt, dass deren Differenzen proportional zur “standard Schwarzschild-Zeit” sind, die (zumindest) jeden stationären Pfad (einzeln) gleich- bzw. standardmäßig mit reellen Zahlen bestreußelt.
> Damit kann er den (Koordinaten-)Radius R(t) des Sterns zu einer beliebigen Zeit t bestimmen und findet, dass stets R(t) > R* nebst R(t) → R* asymptotisch für t → +∞ gilt, wobei R* den Schwarzschild-Radius der Sternmasse bezeichne.
Da es sich bei den “R” um Koordinaten-Werte handeln soll, bezeichnet R* also ebenfalls einen bestimmten Koordinaten-Wert, der offenbar so definiert ist, dass
R* := Limit_{ t → +∞ }_[ R(t) ],
wobei sich die genauen Werte R(t) (für jeden gegebenen Koordinaten-Wert t) aus der hinreichend detaillierten Festlegung des zugrundegelegten Modells (einschl. Spezifizierung der “Höhe” des geforderten stationären Beobachters insbesondere “über der Photonsphere”, und der Angabe der “Proportionalitätskonstante” der Werte t gegenüber “standard Schwarzschild-Zeit“) ergeben.
> für eine auf der Oberfläche des kollabierenden Sterns befindliche Uhr [vergeht] eine endliche Zeitspanne,
… die Dauer z.B. von ihrer Anzeige der Passage des stationären Beobachters (“bei Versuchsstart”) …
> bis R* erreicht wird.
Das finde ich ungenau formuliert. (Und das ist der wesentliche Anlass meines Kommentars.)
Richtiger:
Der Oberflächenstaub erreicht das Ereignis, für das der stationäre Beobachter (“in weiser Voraussicht”) die Koordinaten-Werte
(t, R[t]) = (∞, R*)
vorgesehen hat.
(Was für den betreffenden Oberflächenstaub selbst möglicherweise insbesondere daran erkennbar gewesen sein mag, dass “die Karlhede-Invariante” dabei verschwand bzw. ihr Vorzeichen wechselte.)
Das heißt aber (selbstverständlich?) nicht, dass der stationäre Beobachter “die mit seiner eigenen Uhr gemessene Zeit t als Zeitkoordinate” des Wertes t = ∞ erhalten, “ den (Koordinaten-)Radius R(t) des Sterns zu Zeit t = ∞ bestimmt und ” R* gefunden hätte.
Der Wert R* wird nicht in dem selben und voll-umfänglichen Sinne unter Mitwirkung der Uhr des stationären Beteiligten “erreicht“, wie es für “tatsächlich ermittelte (größere)” Koordinatenwerte R(t) zutrifft.
> Idealerweise lebt der [stationäre] Beobachter ewig, dennoch erlebt er nicht die Entstehung eines Horizontes
Der stationäre Teilnehmer nimmt nicht selbst an einer Passage des Horizonts teil, “erlebt” also nicht selbst, weil er vorgegebenermaßen stationär und “außerhalb des Staubsterns” sein und bleiben soll.
Und er kann und wird auch niemals eine Anzeige des (Oberflächen-)Staubes bei Passage des Horizonts sehen.
(Allerdings … kommt mir dabei in den Sinn: Was genau hat eigentlich ein Detektor gesehen, der die bekannten Waveforms noch bis über das Amplituden-Maximum registriert hätte? …)
> sondern beobachtet einen ewig fortdauernden Kollaps des Sterns.
Besser (weil “eigentlicher”):
(Ganz abgesehen von allen praktisch-instrumentellen Einschränkungen.)
> […] wenn bei zwei gleich rasch gehenden Uhren die erste nur eine endliche Zeitspanne misst
… Dauer der Uhr, von welcher Anzeige bis zu welcher Anzeige …
> während dabei
… wobei genau?! (wer, von … bis …?) …
> für die zweite gleichzeitig(!) unendlich viel Zeit verrinnt.
Das meint (hoffentlich !) jedenfalls nicht “gleichzeitig(!)” im Sinne von Einsteins bekannter Definition.
Besser:
” … während die Dauer der anderen (seit Versuchsbeginn, bis irgendeiner weiteren Anzeige im Warten auf das Versuchsende, das allerdings nie eintreten wird) beliebig groß wird.
(Und dabei ist es natürlich auch unerheblich, ob diese beiden Uhren “gleich rasch gehend” gewesen und geblieben wären, oder in wie fern nicht.)
Zur üblichen Radiuskoordinate bei der Schwarzschild-Metrik: Durch die Kugelsymmetrie und den Umstand, dass die Raumzeit statisch ist, sind die radialen Geodäten doch schon festgelegt. Und die Flächeninhalte der entsprechenden Kugelflächen bei konstantem r auch. Insofern ist das übliche r eben gerade keine frei gewählte Koordinate ohne über die Koordinateneigenschaft hinausgehenden Sinn, sondern hat eine direkte physikalische Bedeutung.
Markus Pössel schrieb (22. September 2017 @ 16:00):
> Zur üblichen Radiuskoordinate bei der Schwarzschild-Metrik: Durch die Kugelsymmetrie und den Umstand, dass die Raumzeit statisch ist, sind die radialen Geodäten doch schon festgelegt.
Sicherlich folgen unter den von Chrys oben vorgegebenen Umständen die Bestandteile der Staub-(Stern-)Oberfläche “radialen Geodäten“;
und die Parametrisierungen solcher “radialer Geodäten” durch “standard Schwarzschild-Zeit” und “üblichen Radiuskoordinate” (und natürlich für jeweils konstante geeignete Werte “θ” bzw. “φ”) dürften einander gleichen (wohl sogar hinsichtlich der “Startwerte” von “standard Schwarzschild-Zeit” bzw. von “üblicher Radiuskoordinate“).
> Und die Flächeninhalte der entsprechenden Kugelflächen bei konstantem r auch.
“Flächeninhalt“ wurde offenbar in diesem Blog bisher nur ein einziges Mal erwähnt; und zwar eher beiläufig, ohne nachvollziehbare Definition.
Wie also wäre “Flächeninhalt” definiert bzw. zu messen?,
insbesondere hinsichtlich einer Region, die nicht ausdrücklich flach sein soll und in der folglich z.B. (Verhältnis-)Werte von Raumzeit-Intervallen s^2 gar nicht definiert sind.
p.s.
> […] über die Koordinateneigenschaft hinausgehende[r] Sinn […]
Zur Frage von Koordinaten und koordinatenfreien Darstellungen wartet die gespannte Leserschaft nun seit genau einem Jahr auf “einen gesonderten Blogbeitrag“.
Letztlich würde man beim Flächeninhalt wieder die lokale Flachheit ausnutzen, und infinitesimale Flächeninhalte aufintegrieren.
Markus Pössel schrieb (1. Oktober 2017 @ 09:58):
> Letztlich würde man beim Flächeninhalt wieder die lokale Flachheit ausnutzen
Bitte (endlich!, und \(\LaTeX\)-formatiert!) mal ausführlich vormachen! —
der Grenzwert wovon wäre “lokal flach” zu nennen ??
> und infinitesimale Flächeninhalte aufintegrieren.
Ableiten ist ein nachvollziehbares Handwerk;
und Integrieren ist das Gegenteil.
Sie stoßen (wie schon so oft) an die Grenze, dass mein Blog zumindest einigermaßen allgemeinverständlich bleiben soll. Die exakten mathematischen Definitionen, die Sie sich wünschen, werde ich da nicht stringent einführen können; selbst die “Zwischenstufe” (z.B. für Lehramtsstudierende) bleibt bei mir aus gutem Grund bei Plausibilitätsargumenten. Ich kann mir vorstellen, da wäre Ihnen mit einem guten Fachbuch wirklich eher gedient. Kennen/haben Sie z.B. den Nakahara? Geometry, Topology and Physics?
@Wappler Kurze Anleitung zur Mathematik der Gravitationswellen, gut erklärt.
http://www.ams.org/publications/journals/notices/201707/rnoti-p693.pdf
Viel einfacher kann man die Näherungen wohl nicht machen.
Herr Senf schrieb (4. Oktober 2017 @12:53):
> […] http://www.ams.org/publications/journals/notices/201707/rnoti-p693.pdf […]
> […] Näherungen […]
Na, schönen Dank für den Hinweis auf diese Diskussionsgrundlage.
Darin findet sich folgende ganz bestimmte Näherung (bzw. Auswertung von Grenzwerten), die besondere Relevanz für (vermeintliche?) “Gravitationswellen-Nachweise” hat, um die es zumindest im Titel des obigen SciLogs-Artikels und ganz konkret in meinem direkt anschließenden Kommentar (20. September 2017 @ 11:26) ging:
Die Näherung besteht hier natürlich in der Betrachtung von “short duration motion” (Bahnabschnitte von kurzer Dauer) der Spiegel, d.h. insbesondere im Vergleich zur Periodendauer entsprechend ihrer pendular swing frequency (about 1 Hz); bzw. in der Betrachtung des Grenzüberganges zu beliebig kurzen Dauern der Spiegel.
Die zitierte Beschreibung ist zwar nicht ganz falsch:
Falls dem Interferometer nichts weiter passierte als die Passage einer Gravitationswelle, dann blieb jeder der Spiegel dabei einzeln ruhig hängen, und die (quasi-periodische) Veränderung der Entfernung der Interferometerspiegel voneinander ist ein direkter Indikator der (quasi-periodisch veränderlichen) Krümmung der Region, die die Spiegel enthielt.
Der Umkehrschluss aber, der insbesondere durch den zweiten zitierten Absatz nahegelegt erscheint, ist und bleibt ungültig:
Aus der (eventuellen) experimentellen Feststellung der Veränderung der Entfernung der Spiegel voneinander
folgt nicht mit mathematischer Strenge,
dass alle oder auch nur irgendeiner dieser Spiegel dabei ruhig hängengeblieben wäre; dass ihre horizontalen Bewegungen auch nur näherungsweise als Geodäten beschrieben werden könnten, oder dass sich dabei die Krümmung der Region nachweisbar verändert hätte.
Darauf müsste man zwar niemanden ausdrücklich hinweisen, dem hinreichende Sorgfalt zuzutrauen ist. Aber es gilt ja auch jenen beizukommen, die sich und anderen ganz
selbstverständlichallgemeinverständlich gelbe Paste in die Augen schmieren (lassen) (würden) …Kann man auch kürzer sagen: Außerhalb der Mathematik folgen wissenschaftliche Erkenntnisse ganz allgemein nicht mit mathematischer Strenge. Sondern es sind immer Modelle und Störeinflüsse im Spiel. Und?
Die Näherung “short duration motion” ist übrigens aus dem folgenden Grunde richtig: Bei LIGO werden etwaige interferometrisch detektierte Schwingungen der Spiegel ja sofort aktiv vom Steuerungssystem abgedämpft. Die Information über die Gravitationswelle steckt dadurch letztlich fast nur in den Kontrollströmen des Steuerungssystems. Der Spiegel bleibt dadurch jeweils sehr nahe an der Ruhelage, mit entsprechend geringer Pendel-Rückstellkraft.
Markus Pössel schrieb (5. Oktober 2017 @ 12:00):
> Außerhalb der Mathematik folgen wissenschaftliche Erkenntnisse ganz allgemein nicht mit mathematischer Strenge.
Da gibt es offenbar verschiedene Ansichten und Abstufungen; vgl. https://en.wikipedia.org/wiki/Exact_sciences
> Sondern es sind immer Modelle und Störeinflüsse im Spiel.
Sofern das zutrifft …
> Und?
… benennt man eventuelle Modell-Annahmen gewissenhaft, und führt ebenso gewissenhaft Abschätzungen von systematischen Unsicherheiten durch, und zwar unter Bezug auf Modell-unabhängige Definitionen.
Dann (und nur dann) setzt man sich ans Telefon und wartet schon. …
p.s.
> Bei LIGO werden etwaige interferometrisch detektierte Schwingungen der Spiegel ja sofort aktiv vom Steuerungssystem abgedämpft. Die Information über die Gravitationswelle steckt dadurch letztlich fast nur in den Kontrollströmen des Steuerungssystems.
Das glaube ich zwar gern (Stichworte: “dark port”, “Drever/Schnupp”);
aber gibt es dazu bitte eine (Barriere-freie) Referenz, die konkret benennt, welche Aktuatoren in welchen Frequenzbändern insbesondere die betreffenden Testmassen gegenüber den jeweiligen Reaktionsmassen geeignet nachführen würden?
> Der Spiegel bleibt dadurch jeweils sehr nahe an der Ruhelage
Jedenfalls ist durchaus vorstellbar, dass die Spiegel beider Arme so schnell nachgeführt würden, dass das Interferometer insgesamt nahezu interferometrisch starr blieb.
(Die in den 5. Oktober 2017 @ 11:36 verlinkten Referenzen dargelegten Vorstellungung der “horizontally free motion” bzw. “treatment as a spacetime geodesic” bezögen sich demnach einigermaßen selbstverständlich auf den Schwerpunkt des jeweiligen Paares von Test- und Reaktionsmasse.
D.h. natürlich nur sofern dahingehend keine “Verwechslungen” vorlägen und sich diese Schwerpunkte stattdessen “horizontal unfrei, nicht-geodätisch, beschleunigt” bewegt hätten.)
Gerade deshalb erscheint ja die “Five-point — Ten-arm — Curvature Detector”-Methode (als der hier schon öfters erwähnten LISA-Ausbaustufe) durchaus realisierbar.
Ich sehe in dem Wikipedia-Artikel jetzt keine Aussage, die den Messungen in Physik, Biologie, Chemie etc. denselben absoluten Status zusprechen würde wie einem mathematischen Beweis. Was die Gravitationswellen angeht haben die betreffenden Forscher ihre Annahmen und ihre Abschätzungen von systematischen Unsicherheiten ja nun wirklich sehr ausführlich dargelegt. Modell-unabhängige Definitionen? Welches einigermaßen anspruchsvolle experimentelle Ergebnis kennen Sie denn, in das nicht bei der Interpretation der Messungen zwangsläufig z.B. Modellannahmen über die verwendeten Messinstrumente eingingen? Ich habe nach wie vor den Eindruck, dass Sie aus für mich nicht nachvollziehbaren Gründen an diese bestimmte Messung unrealistisch hohe Ansprüche anlegen.
Zum Steuerungssystem: Da müssten Sie schon selbst etwas Zeit investieren, nachzuforschen. Im Prinzip sind auf https://dcc.ligo.org so gut wie alle technischen Beschreibungen aller Subsysteme und viele Berichte über diverse Tests barrierefrei verfügbar.
Markus Pössel schrieb (5. Oktober 2017 @ 21:42):
> Ich sehe in dem Wikipedia-Artikel jetzt keine Aussage, die den Messungen in Physik, Biologie, Chemie etc. denselben absoluten Status zusprechen würde wie einem mathematischen Beweis.
Ach so.
(Ich sehe übrigens in dem oben verlinkten Wikipedia-Artiklel über [[Exact sciences]] noch nicht einmal eine ausdrückliche Erwähnung von “Biologie, Chemie etc.” …)
Trotzdem sei auch auf den Begriff Richtigkeit (engl. “trueness”) hingewiesen, der insbesondere im Zusammenhang mit Messungen zu beachten ist.
> Was die Gravitationswellen angeht haben die betreffenden Forscher ihre Annahmen und ihre Abschätzungen von systematischen Unsicherheiten ja nun wirklich sehr ausführlich dargelegt.
Ich vermisse (bisher) Betrachtungen der Konsequenzen für den Fall, dass die insbesondere vom LIGO Science Steering Committee geäußerte Annahme, bestimmte Bestandteile des Versuchsaufbaus seien “horizontally free-moving“ nicht erfüllt worden wäre;
insbesondere für Beschleunigungen in Größenordnungen, für die die eingesetzten “physical environmental monitoring“-Systeme nicht empfindlich waren.
(Hinsichtlich der von LIGO implementierten Gertsenshtein/Pustovoit/Weiss-Methode müsste man dabei wohl von “irreducible background” sprechen.)
> Im Prinzip sind auf https://dcc.ligo.org so gut wie alle technischen Beschreibungen aller Subsysteme und viele Berichte über diverse Tests barrierefrei verfügbar.
Im Prinzip könnte jemand, der auf der betreffenden Seite “Login”-Privilegien hat und hier mitliest, uns mal einen Tip geben, wo genau die Betriebs-Werte (Spannungs-Amplituden?) der Aktuatoren “zwischen Testmassen und Referenzmassen” abrufbar sind, die zusammen mit den bekannten Signal-Formen aufgezeichnet wurden. …
> Modell-unabhängige Definitionen? […]
Ein konkretes und einigermaßen übersichtliches Beispiel bietet die Definition wie zu messen ist, ob jeweils zwei “Enden” bzw. Bestandteile eines “Stabes” gegenüber einander “starr” gewesen und geblieben wären, oder in wie fern nicht;
für deren Darstellung und Diskussion der an Chrys gerichtete Kommentar 5. Oktober 2017 @ 22:09 einen (mir willkommenen) Anlass bietet.
(Hoffentlich wird uns dafür eine eigene, \(\LaTeX\)-befähigte SciLogs-Seite zur Verfügung gestellt! ;)
> Ich habe nach wie vor den Eindruck, dass Sie aus für mich nicht nachvollziehbaren Gründen an diese bestimmte Messung unrealistisch hohe Ansprüche anlegen.
Ich halte Einsteins Anspruch gerade hier nach wie vor für vertretbar:
Aber natürlich müssen oder mussten nicht alle diesem Anspruch gerecht werden (sondern mögen sich stattdessen bestimmten von Einstein in diesem Zusammenhang erwähnten “Täuschungen” hingeben);
auch nicht, wenn sie (durch Erfüllung gewisser anderer Ansprüche) erhebliche Vermögen machten, oder daraus (in Verpflichtung auf gewisse andere Ansprüche) gestiftete Preise verleihen …
wieso wird hier immer von unendlicher Zeit geredet, ich denke schwarze Löcher lösen sich auch wieder auf (Hawking)? Dann muss man doch nur eine begrenzte Zeit “warten”.
naja,
begrenzt kann ziemlich lange sein, fast wie unendlich, so 10^100,
und “unendlich” ist keine greifbare Zahl – eher Hilfskonstrukt für Philosophie.
Grüße Dip
War es das gewesen: Pressekonferenz der ESO am Mo 16.10.17 16:00 MESZ
“über noch nie dagewesene Entdeckung” mit 70(!) Observatorien
https://www.eso.org/public/germany/announcements/ann17071/
Gespannt – Dip
Das sieht auf alle Fälle spannend aus!
Heute 1 Tag nach den Pressekonferenzen sind alle Artikel
auf https://arxiv.org/list/astro-ph/new abrufbar WW170817
von 1710.05431 durchgängig bis 1710.05463, also 33 Stück