Was Meta-Analysen können und was nicht

Gerade war mit der Cochrane-Masken-Studie eine Meta-Analyse in den Schlagzeilen – und das zu einem politisch sehr aufgeladenen Thema. Für diejenigen, die verstehen wollen, was die Hintergründe der verwendeten Methodik sind, hier eine Auffrisch- oder Erweiterungseinheit dazu, was Meta-Analysen sind, was sie gut können und was sie nicht so gut können.

Experimente mit Kontrolle und Endpunkten

Wie können wir Effekte mit Hilfe von Studien nachweisen? Die wohl häufigste Situation in der Medizin ist der Versuch, die Wirksamkeit bestimmter therapeutischer Eingriffe zu überprüfen, vereinfacht: Wenn ich Patient*innen mit Krankheit X das Medikament Y verabreiche, geht es ihnen danach wesentlich besser oder nicht?

All das muss man natürlich noch weiter konkretisieren, bevor man quantitative Aussagen treffen kann, aber dazu gibt es eine Art Standard-Vokabular, das vom konkreten Fall unabhängig ist. Für meine Studie teile ich die Patient*innen, deren Daten ich erhebe, in zwei Gruppen. Die Mitglieder der Experimentalgruppe bekommen das Medikament (in vorgegebener Dosierung, Häufigkeit, etc. – das muss ich natürlich festlegen), die Mitglieder der Kontrollgruppe bekommen das Medikament nicht. (Idealerweise ist dabei weder den Patient*innen noch den Experimentator*innen bekannt, wer zur Experimentalgruppe gehört und wer zur Kontrollgruppe – das ist dann eine Doppelblindstudie. Aber um diesen Aspekt geht es in diesem Blogbeitrag nicht.)

Weiterhin definiere ich Endpunkte, englisch “Outcomes”. Ein einfaches Beispiel: Meine Patient*innen, ob in Experimentalgruppe oder Kontrollgruppe, werden gesund oder sie werden es nicht. (Auch da muss ich natürlich spezifisch sein: Zu welchem Zeitpunkt – eine Woche nach Therapiebeginn, zwei Wochen, drei? – überprüfe ich die Gesundheit? Was sind meine Kriterien dafür – soll ein Ausschlag verschwinden, ein Laborwert normal sein, oder..?)

Wahrscheinlichkeiten, Häufigkeiten und Stichprobeneffekte

Und dann kann es auch schon losgehen und quantitativ werden. Nehmen wir an, ich hätte 22 Patient*innen in meiner Experimentalgruppe und 20 Patient*innen in meiner Kontrollgruppe. Aus der Experimentalgruppe werden 17 Teilnehmer*innen gesund, aus der Kontrollgruppe nur 10 Teilnehmer*innen. Was sagt mir das? Nun gut: Aus meiner Experimentalgruppe sind 77% gesund geworden, während in der Kontrollgruppe (und damit vermutlich: von alleine) rund 50% gesund geworden sind. Ein klarer Vorteil für die Experimentalgruppe. Das Medikament wirkt. Oder?

So einfach ist es natürlich nicht. Insbesondere haben wir ja gesehen: Auch in der Kontrollgruppe sind eine Reihe Patient*innen gesund geworden. Ob man gesund wird oder nicht hängt also auf alle Fälle nicht alleine von der Medikamentengabe ab. Nehmen wir an, in unserer Spielzeugsituation sei es tatsächlich so einfach, dass es zwei Wahrscheinlichkeiten gibt: eine davon, sagen wir: 50%, gibt an, wie wahrscheinlich es ist, dass jemand, der das Medikament bekommt, anschließend gesund wird. Die andere, sagen wir: 35% Prozent, gibt an, dass jemand, der das Medikament nicht bekommt, anschließend gesund wird.

Da wir über Wahrscheinlichkeiten reden, spielt der Zufall eine Rolle. Das kennen Sie vielleicht vom Würfeln. Wenn sie mit einem Würfel 36 mal würfeln, und zwar selbst wenn es ein perfekter Würfel wäre, dann würden Sie mit großer Wahrscheinlichkeit keine Würfelserie bekommen, in der jeder der sechs möglichen Zahlenwerte exakt 6 Mal oben liegt. Ich habe das gerade mal ausprobiert und komme stattdessen auf:

Zahlenwert	1	2	3	4	5	6
Wie oft gewürfelt	6	2	9	4	7	8

Das sieht auf den ersten Blick natürlich nicht so aus, als hätte ich es mit einem fairen Würfel zu tun gehabt. Aber der erste Blick trügt in diesem Falle. Dass die Häufigkeiten vom Idealfall – auf jeden Zahlenwert entfällt ein Sechstel der Würfelergebnisse – abweichen ist ein reiner Stichprobeneffekt. Würde ich mein Experiment häufiger durchführen, dann würden meine Häufigkeiten den wahren Wahrscheinlichkeitswerten dafür, die verschiedenen Zahlen zu würfeln, immer näher kommen.

Im wirklichen Leben kann ich immer nur eine endliche Anzahl von Experimenten durchführen – je nach experimentellem Aufwand vielleicht auch gar keine allzu große. Tausend Würfelwürfe mag ich mit viel Ausdauer noch hinbekommen. Kinische Studien sind schon deutlich aufwändiger – da kann es sein, dass allein schon die Kosten, oder auch die Anzahl und Größe der teilnehmenden Krankenhäuser, meine Teilnehmer*innenzahl beschränkt.

Und damit spielen zwangsläufig Stichprobeneffekte eine Rolle. Die Tatsachen, dass ich es zum einen mit Zufallseffekten, zum anderen mit Stichproben beschränkter Größe zu tun habe, führt mathematisch-zwangsläufig dazu, dass meine Schätzungen für Effektstärken mit bestimmter Wahrscheinlichkeit von den tatsächlichen Effektstärken abweichen. In meinem Beispiel oben sind die Häufigkeiten 77% bzw. 50% meine Schätzwerte für die zugrundeliegenden Wahrscheinlichkeiten, dass Menschen mit Krankheit X entweder mit oder ohne Gabe des Medikaments gesund werden. Aber wenn diese Schätzungen aufgrund der endlichen Stichprobengröße von den tatsächlichen Wahrscheinlichkeitswerten abweichen, wie kann ich dann sicher sein, nicht nur einem ungünstigen Zufall aufgesessen zu sein? Es könnte ja sein, dass die zufälligen Schwankungen, die meine endliche Stichprobengröße mit sich bringt, mir den Unterschied zwischen 77% und 50% lediglich vorgaukeln, während das Medikament in Wirklichkeit nichts zur Heilung beiträgt. Tatsächlich ist der Unterschied zwischen den tatsächlich zugrundeliegenden Wahrscheinlichkeiten (die ich aber nur deswegen weiß, weil ich meine simulierte Version so definiert habe und deswegen so etwas wie ein allwissender statistischer Beobachter bin) und den Schätzungen ja beträchtlich.

Das ist eine zentrale Grundfrage, die man in dieser Art von Experiment zu beantworten bzw. zumindest zu quantifizieren versucht. Eine Zwischenbemerkung: Wahrscheinlichkeiten spielen dabei auf zwei Ebenen eine Rolle. Einerseits modelliere ich den Experimentalverlauf als Zufallsexperiment – für die Teilnehmer*innen gibt es eine Wahrscheinlichkeit, mit Medikamentengabe gesund zu werden und eine Wahrscheinlichkeit, ohne Medikamentengabe gesund zu werden. Aber es gibt eben noch eine zweite Ebene. Mein Experiment mit seiner Stichprobe ist ein Versuch, mit Hilfe einer Stichprobe Wahrscheinlichkeiten abzuschätzen. Und da gibt es dann wiederum bestimmte Wahrscheinlichkeiten dafür, mit dieser Schätzung näher am wahren Wert oder weiter entfernt davon zu liegen. Auch das ist ein Zufalls-Experiment, eine Ebene höher!

Relatives Risiko, Vierfeldertafel

Einen technischen Schlenker müssen wir an dieser Stelle noch unternehmen. Es gibt an dieser Stelle mehrere Möglichkeiten, die Effektstärke zu definieren. Wir könnten beispielsweise die Unterschiede der Gesundheits-Häufigkeiten als Maß nehmen – diesem Maß nach wäre die geschätzte Effektstärke in unserem Beispiel 77%-50% =27 Prozentpunkte. Üblicher ist bei dieser Art von Studien aber ein anderes Maß: das relative Risiko, auch Risikoverhältnis genannt, abgekürzt RR. Das RR ist das Verhältnis der Wahrscheinlichkeit, mit der ein bestimmtes Ereignis (z.B. “Testperson wird gesund”) in der Experimentalgruppe auftritt zur Wahrscheinlichkeit, mit der jenes Ereignis in der Kontrollgruppe auftritt. Die Abschätzung für den RR in meinem Zahlenbeispiel ist entsprechend 77% geteilt durch 50%, entsprechend einem geschätzten RR von 1.54.

Eine sprachliche Feinheit: “Risiko” klingt im Alltag negativ. Es hat sich bei solchen Studien aber eingebürgert, das RR für alle Arten von Ereignis zu verwenden, auch für positive. So kann z.B. auch ein Ereignis wie “nach einem Jahr noch am Leben sein” mit einem RR von 1.13 beschrieben werden, obwohl ein erhöhtes Risiko im Alltagsverständnis ja etwas Negatives, eine erhöhte Chance zu überleben etwas Positives ist.

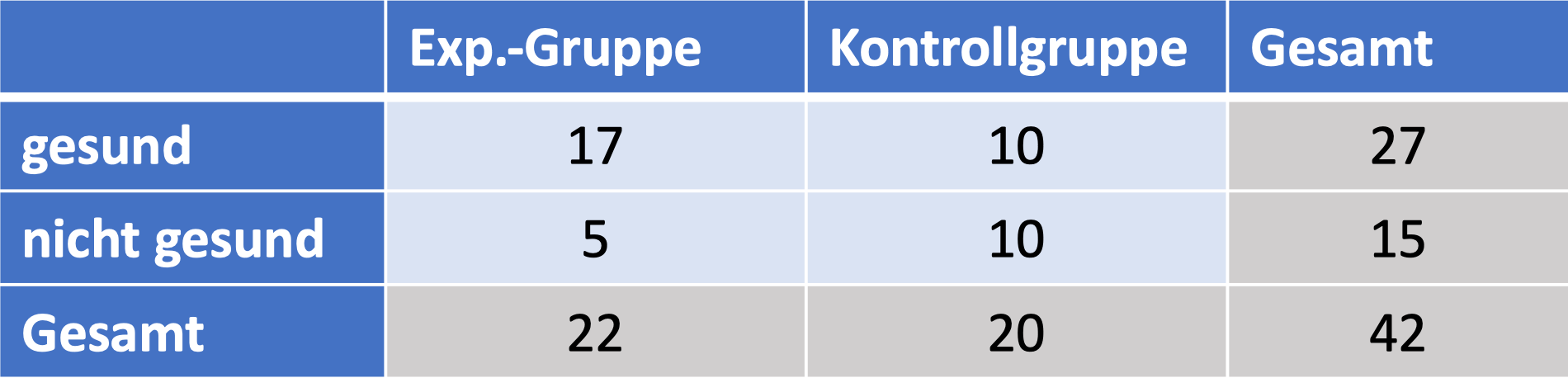
Bevor es weitergeht, hier noch ein weiteres nützliches Werkzeug: Für die Art von Analyse, die wir hier machen, ist es hilfreich, die Daten in einer sogenannten Vierfeldertafel aufzuschreiben. Für mein Zahlenbeispiel sieht das so aus:

Das ist eine sogenannte Vierfeldertafel, wobei die vier namensgebenden Felder hier hellblau dargestellt sind: Anzahl der Gesunden in Experimentalgruppe, Anzahl der Kranken in Experimentalgruppe, dasselbe für die Kontrollgruppe.

Dieselbe Aufstellung kann man natürlich auch für den allgemeinen Fall machen, jenseits unseres speziellen Beispiels:

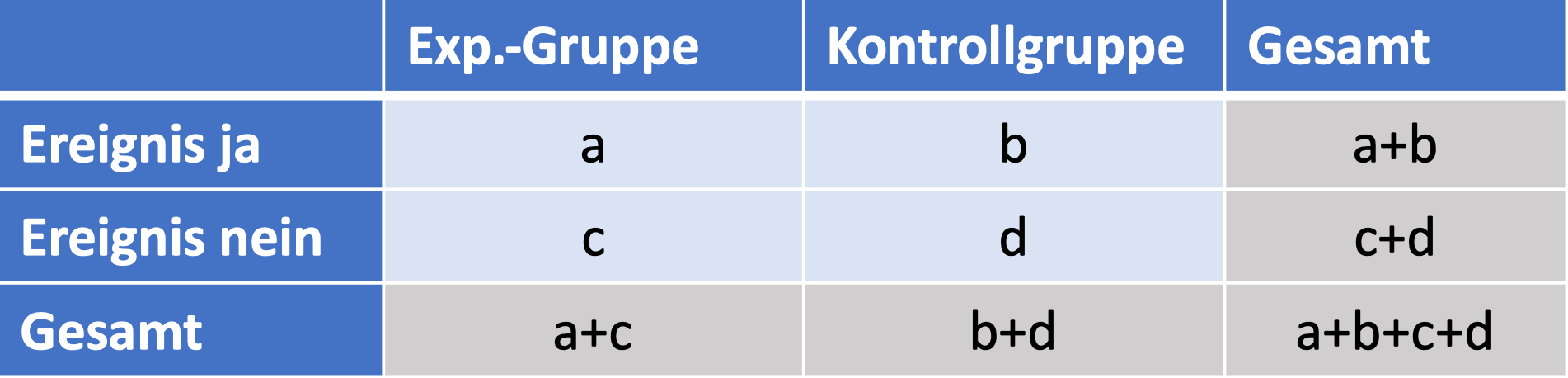Damit ist die Häufigkeit (also auch unsere Schätzung für die Wahrscheinlichkeit), dass das Ereignis für jemanden aus der Experimentalbgruppe eintritt, \(a/(a+c),\) für jemanden aus der Kontrollgruppe \(b/(b+d),\) und unser Schätzwert für das relative Risiko ist $$ RR = \frac{a/(a+c)}{b/(b+d)}. $$

Bester Schätzwert und Vertrauensintervall

An dieser Stelle müssen wir uns etwas an Wissen aus der Statistik borgen, das ich hier nicht ableite. Angenommen, ich nehme eine größere Anzahl jeweils nicht allzu kleiner Stichproben (als Faustregel nimmt man dabei an: mehr als 30 Fälle pro Stichprobe, aber der Wert ist nicht in Stein gemeißelt). Dann lässt sich die Art und Weise, wie aus jeder Stichprobe gesondert abgeleitete Schätz-Mittelwerte um den wahren Wert streuen, in guter Näherung mit einem Wahrscheinlichkeits-Modell beschreiben, dass “Normalverteilung” genannt wird. Dahinter steht der sogenannte “zentrale Grenzwertsatz”, der ganz allgemein besagt, dass die Normalverteilung eine gute Näherung zur Beschreibung der Wahrscheinlichkeiten von Werten ist, die sich als Summe von nicht allzu wenigen Zufallswerten ergeben. Eine kleine Komplikation kommt an dieser Stelle noch dazu: Verhältnisse wie unser relatives Risiko haben diese Summen-Eigenschaft nicht, aber wenn wir statt des RR den natürlichen Logarithmus ln(RR) betrachten, dann dürfen wir die Näherung anwenden.

Unter diesen Voraussetzungen liefert uns die Statistik den sogenannten Standardfehler, englisch standard error und deswegen oft SE abgekürzt, für ln(RR) als einfache Funktion der aus der Vierfeldertafel ablesbaren Werte a, b, c, d: $$SE_{\mbox{ln}(RR)} = \sqrt{\frac{1}{a}+\frac{1}{b}-\frac{1}{a+c} – \frac{1}{b+d}}.$$ Die Details der Formel sind hier gar nicht so interessant, aber halten wir mal fest: So kompliziert ist die Formel gar nicht, nichts was über Schulwissen zu Brüchen und Wurzeln hinausginge. (In der Praxis überlässt man das Ausrechnen dann in der Regel sowieso den Computern.)

Mit dem Standardfehler wiederum kann man das sogenannte 95%-Vertrauensintervall oder 95%-Konfidenzintervall, englisch confidence interval und deswegen CI abgekürzt, ausrechnen: die Untergrenze dieses Intervalls liegt bei unserem Schätzwert für ln(RR) minus 1.96 mal SE, die Obergrenze liegt beim Schätzwert plus 1.96 mal SE. Da ln(RR)-Werte nicht allzu allzu anschaulich sind, transformiert man an dieser Stelle obere und untere Grenze des Vertrauensintervalls wieder mit Hilfe der Exponentialfunktion zurück und erhält dann das Vertrauensintervall für RR selbst.

In meinem Zahlenbeispiel liegt das geschätzte RR bei 1.545, der natürliche Logarithmus davon bei ln(RR)= 0.435,  der Standardfehler SE für ln(RR) der obigen Formel nach bei 0.252, die Untergrenze des Vertrauensintervalls entsprechend bei 0.435-1.96*0.252=-0.058 die Obergrenze bei 0.435+1.96*0.252=0.929. Wenden wir auf Unter- und Obergrenze die Exponentialfunktion an, dann landen wir bei 0.944 als Untergrenze und 2.531 als Obergrenze. In einer entsprechenden Veröffentlichung dürften sie im Allgemeinen aber nicht all diese Zwischenschritte finden, sondern dort steht dann nur so etwas wie:

RR 1.55, 95% CI 0.94 bis 2.53

oder vielleicht auch nur

RR 1.51 [0.94, 2.53].

Die eigentlichen Rechnungen führt wie gesagt der Computer aus, für uns ist wichtig: die Interpretation des Ganzen. Und die ist wie folgt: Wenn wir unser gesamtes Experiment mit derselben Stichprobengröße wiederholen würden, wieder und wieder (in der mathematischen Idealisierung unendlich oft, in der Praxis “häufig genug”), und wenn wir dann in der genannten Weise für jedes dieser Experimente das 95%-Vertrauensintervall ausrechnen würde, dann würde der wahre Wert für den Parameter RR für rund 95% der wiederholten Experimente in dem geschätzten Vertrauensintervall liegen, und für nur 5% der genannten Experimente außerhalb.

Üblicherweise führt man solche Wiederholungen zwar nicht durch, aber die Interpretation lässt sich auch auf ein einzelnes solches Experiment und das abgeleitete 95%-Vertrauensintervall anwenden. Wenn wir für unser einzelnes Experiments ein 95%-Vertrauensintervall für den zu schätzenden Wert (in unserem Fälle RR) abgeleitet haben, dann beträgt die Wahrscheinlichkeit, dass sich der wahre Wert in jenem geschätzten Vertrauensintervall befindet, 95%. Salopp gesagt sind wir nicht zu 100% sicher, aber immerhin zu 95% (“95% confidence”), dass der wahre Wert in unserem 95%-Vertrauensintervall liegt.

Damit können wir dann auch zu der Ausgangsfrage zurückkehren: Können wir aus den Ergebnissen schließen, dass die Maßnahme wirkt, oder könnte der Umstand, dass das relative Risiko (im positiven Sinne) größer als eins ist, auch ein reiner Stichprobeneffekt, also Zufall sein? An dieser Stelle wird wichtig, dass der neutrale RR-Wert RR=1, also der Fall, dass das Risiko für Experimentalgruppe und Kontrollgruppe genau gleich hoch liegt, für mein Zahlenbeispiel im 95%-Vertrauensintervall liegt. In dem Falle müssen wir sagen: Sorry, alleine anhand unserer Zahlen hier können wir nicht unterscheiden, ob das Medikament eine Wirkung hat oder nicht. Läge RR=1 dagegen außerhalb unseres 95%-Vertrauensintervalls, dann könnten wir stattdessen sagen: Wir sind uns zu 95% sicher, dass der tatsächliche RR-Wert in unserem Vertrauensintervall liegt, also insbesondere vom neutralen Wert 1 abweicht. Die Chance, dass wir uns irren, wenn wir die Aussage treffen, der wahre Wert liege in unserem geschätzten Intervall, beträgt lediglich 5%. Diese Restwahrscheinlichkeit wird als Signifikanzniveau bezeichnet. Liegt die 1 nicht im 95%-Vertrauensintervall, konstatieren wir entsprechend eine “signifikante Abweichung” vom neutralen Wert (mit Signifikanzniveau 5%, oft geschrieben als \(\alpha<0.05 \)).

Man muss an dieser Stelle einigermaßen aufpassen, wie man über jene 5% spricht. Der Konstruktion nach gilt: Ist das Ergebnis unseres Experiments signifikant, liegt also RR=1 außerhalb des 95%-Vertrauensintervalls, dann beträgt unseren Daten nach die Wahrscheinlichkeit, dass die Unterschiede zwischen Experimentalgruppe und Kontrollgruppe rein aufgrund von Stichproben-Effekten (also zufällig) zustandekommen, 5% oder noch weniger. Umgekehrt gilt aber nicht, dass man, wenn die 1 doch im 95%-Vertrauensintervall liegt, nachgewiesen hätte, dass es keinen realen Effekt gibt. Wir können in diesem Falle nämlich insbesondere nicht unterscheiden, ob es keinen realen Effekt gibt oder ob es zwar einen realen Effekt gibt, aber unsere Stichprobe nicht groß genug war, um ihn nachweisen zu können. (Das wird auch in wissenschaftlichen Veröffentlichungen nicht immer richtig formuliert, was wiederum zu heftigen Diskussionen geführt hat.)

Noch eine technische Anmerkung: Ein Signifikanzniveau von 5% ist zwar üblich, bietet aber keinen allzu großen Schutz davor, Zufallsschwankungen aufzusitzen. Vereinfacht gesagt: Wenn ich 20 Studien mit jeweils diesem Signifikanzniveau habe, dann kann ich erwarten, dass eine jener Studien mir fälschlich einen Effekt als signifikant verkauft, der in Wirklichkeit doch durch Zufallsschwankungen zustandekam. Manche Studien wählen deswegen ein höheres Signifikanzniveau, nämlich 1%, und entsprechend ein 99%-Vertrauensintervall. Die obige Rechnung ist dann fast dieselbe, außer dass man bei Ober- und Untergrenze den numerischen Faktor 1.96 jeweils durch 2.575 ersetzen sollte. Dann wird das Vertrauensintervall entsprechend größer; liegt RR=1 dann trotzdem noch außerhalb des Intervalls, ist die Wahrscheinlichkeit, dass dieser Umstand irrtümlich eintrat, entsprechend geringer.

Meta-Analysen oder wenn mehrere Studien an einem Strang ziehen

Der Knackpunkt bei solchen Studien ist häufig die Stichprobengröße. In einer idealen Welt mit unbegrenzten Forschungsgeldern und perfekt vernetzten Kliniken, die zudem personell so gut ausgestattet sind, dass die Mitarbeiter*innen freudig strahlend einwilligen, wenn man fragt, ob sie bei einer klinischen Studie helfen könnten, bekäme man mit einiger Wahrscheinlichkeit (hah!) für so gut wie alle interessanten Effekte aussagekräftige klinische Studien hin. In der wirklichen Welt sieht das leider anders aus. Und das ist natürlich frustrierend. Da hat man eine Studie durchgeführt, das Ergebnis ist nicht signifikant, und – ja, was? Das heißt ja wie gesagt nicht, dass der Effekt nicht vorhanden wäre, sondern es heißt, dass sich mit der betreffenden Studie kein entsprechender Effekt nachweisen ließ.

Gerade bei Therapieformen, die von breiterem Interesse sind, passiert stattdessen zudem häufig etwas anderes. Dann machen sich unabhängig voneinander mehrere Gruppen daran, entsprechende klinische Studien durchzuführen, jede Gruppe mit ihren begrenzten Ressourcen. Vielleicht ist der Effekt in allen diesen Studien nicht signifikant. Vielleicht in einigen. In solch einer Situation möchte man ja eigentlich sagen: Hey, rauft euch da bitte mal zusammen! Macht eure Studie gemeinsam! Einigt euch auf ein gemeinsames Studienprotokoll! Gemeinsam bekommt ihr doch eine viel größere Stichprobe hin als getrennt!

In der Praxis funktioniert das natürlich bei weitem nicht immer (auch wenn sich natürlich schon bei der Organisation der getrennten Studien typischerweise verschiedene Institutionen zusammentun). Die nächstbeste Möglichkeit ist dann, zumindest im Nachhinein so etwas wie eine zusammenfassende Auswertung jener Studien durchzuführen. Diese Art von Auswertung heißt Meta-Analyse.

Nehmen wir erst einmal den einfachsten Fall an, dass nämlich jene getrennten Studien im wesentlichen dasselbe getestet haben – gleiche Behandlung (was natürlich durch entsprechende Leitlinien und deren Empfehlungen begünstigt wird und deswegen gar nicht soooo unwahrscheinlich ist), gleiche Erfolgskriterien (z.B. “Gesundheit nach einem Monat Behandlung”), vergleichbare Patienten-Populationen. In dem Falle wäre das einfachste Vorgehen, man hätte die entsprechenden Rohdaten zur Verfügung, also in unserem Beispiel die vier Werte aus der Vierfeldertafel – wie viele Gesundete/Kranke in der Experimentalgruppe und in der Kontrollgruppe. Dann trägt man dann all diese individuellen Daten in eine große Vierfeldertafel ein, freut sich darüber, dass die Gesamt-Stichprobe nun so groß ist, und bekommt hoffentlich ein aussagekräftigeres Gesamtergebnis. Das wäre dann eine sogenannte “Meta-Analyse mit individuellen Teilnehmerdaten“, englisch meta analysis with individual participant data und deswegen abgekürzt IPD-MA. Mit einfachen Daten wie bei der Vierfeldertafel mag man die entsprechenden Informationen sogar in den wissenschaftlichen Veröffentlichungen finden. Bei komplizierteren Untersuchungen wäre man darauf angewiesen, dass die Studienleiter*innen einem die Rohdaten zuschicken – und da herrscht leider nicht selten eine Drachenschatz-Mentalität vor. Auch wenn sich die wissenschaftliche Gemeinschaft im Prinzip einig ist, dass das Zugänglichmachen von Daten zum Zwecke der Überprüfung/Nachvollziehbarkeit ein Teil guter wissenschaftlicher Praxis ist, die wirkliche Praxis sieht leider so aus, dass die betreffenden Gruppen ihre Rohdaten mehr oder weniger eifersüchtig hüten. [Winkt müde in Richtung der Forscher*innen der Hamburger COPSY-Studie.]

Meta-Analyse mit festen Effekten

Häufiger liegen die Ergebnisse der verschiedenen Studien, die dasselbe untersucht haben, nur in Form zusammenfassender Angaben vor, im Minimalfalle als Angabe zur Effektstärke und zu ihrem Standardfehler. In unserem Beispiel war die Effektstärke das relative Risiko RR bzw. für die eigentlichen Rechnungen der natürliche Logarithmus RR, und die Angabe des Standardfehlers SE für jenen natürlichen Logarithmus. (Äquivalent dazu wäre die Angabe des 95%-Vertrauensintervalls.)

Unter diesen Voraussetzungen – viele Studien, die alle im wesentlichen denselben Effekt zu messen versuchen, Effektstärke und Standardfehler für jede Studie sind bekannt – liefert die sogenannte Meta-Analyse mit festen Effekten, englisch fixed-effect meta analysis, eine gute Möglichkeit, die Daten der einzelnen Studien sinnvoll zusammen auszuwerten, die Stichprobeneffekte dadurch zu reduzieren und am Ende ein ähnlich gutes Ergebnis zu erhalten als hätte man gleich eine einzige einheitliche Studie mit entsprechend größerer Stichprobe gemacht. Das “fester Effekt” bzw. “fixed effect” bezieht sich darauf, dass dieses Verfahren davon ausgeht, dass all jene Studien tatsächlich denselben Effekt mit derselben Effektgröße (z.B. demselben wirklichen RR-Wert) abschätzen, und dass die Unterschiede zwischen den verschiedenen Schätzwerten, die jene Studien liefern, auf Stichprobeneffekte zurückzuführen sind.

Ich habe als Teil meiner Simulation hier ingesamt 5 Studien erzeugt. Basis meiner Simulation ist der (in meiner simulierten Welt dann wahre) Wahrscheinlichkeitswert von 0.5 dafür, dass ein*e Patient*in mit Medikamentengabe gesund wird und 0.35 dafür, dass ein*e Patient*in ohne Medikamentengabe (Kontrollgruppe) gesund wird.

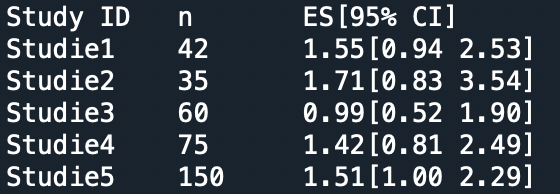
Hier sind die Ergebnisse meiner Studien zusammengefasst. Die erste der Studien hatte ich oben bereits als Beispiel benutzt:

Das n gibt dabei die Gesamt-Teilnehmerzahl an. ES steht für die Effektstärke, in diesem Falle also das relative Risiko RR. In eckigen Klammern dahinter steht das 95%-Vertrauensintervall, berechnet wieder über den Umweg über ln(RR). Was bei weitem nicht zwangsläufig ist, aber sich zufällig so ergeben hat: In keiner der fünf Studien ist der Effekt signifikant. Selbst bei Studie5 nicht, denn wenn man eine Nachkommastelle mehr mitnimmt, liegt die Untergrenze des Vertrauensinterval bei 0.997. Der neutrale Wert RR=1 ist bei allen diesen Studien im 95%-Vertrauensintervall enthalten.

Bei der Meta-Analyse mit einem Modell fester Effekte bildet man einen gewichteten Mittelwert der Effektstärken der einzelnen Studien. Wir rechnen dabei wiederum mit den Logarithmen der Effektstärken. Genutzt wird dabei nicht der normale Mittelwert, also die Summe aller fünf Logarithmen geteilt durch 5, sondern die Studien bekommen in der Kombination unterschiedlich großes Gewicht. Naheliegend wäre eine Gewichtung nach der Teilnehmerzahl, denn es sollte klar sein, dass eine Studie mit 150 Teilnehmer*innen wie Studie5 bereits deutlich mehr an Information enthält, und einen kleineren Stichprobenfehler aufweist, als Studie2 mit nur 35 Teilnehmer*innen. Wenn wir die Effektstärken-Werte (oder hier eben ihre Logarithmen) kombinieren, dann sollte entsprechend Studie5 ein höheres Gewicht erhalten, also mehr Einfluss auf das Endergebnis bekommen, als Studie2.

Das Standardverfahren gewichtet zwar nicht mit der Teilnehmerzahl, macht aber etwas sehr ähnliches. Das Gewicht, das jede Studie bekommt, ist der Kehrwert des Quadrats ihres Standardfehlers SE. Typischerweise ist diese Größe proportional zur Teilnehmerzahl – das sieht man oben in der Wurzelformel für den Standardfehler für die Schätzung von ln(RR): a, b, c, d sind jeweils das Produkt der Gesamt-Proband*innenzahl und einer Häufigkeit (z.B. a das Produkt von “Häufigkeit des Gesundheits-Ergebnisses in der Proband*innengruppe” und Gesamt-Proband*innenzahl). Damit ist der Standardfehler proportional zum Kehrwert der Wurzel der Gesamt-Proband*innenzahl, und der Kehrwert seines Quadrats proportional zur Proband*innenzahl. (Wer im Studium schon einmal zur Auswertung von Experimentaldaten mit Normalverteilungen gearbeitet hat, wird sich vielleicht erinnern: Auch da ist der Standardfehler gleich der Standardabweichung der Grundgesamtheit geteilt durch Wurzel aus N – das ist also dieselbe Situation.)

Bei einem gewichteten Mittelwert bildet man für jeden Beitrag das Produkt aus Gewichtsfaktor (hier: Kehrwert des Quadrat des Standardfehlers) und Wert (hier: Logarithmus von RR) und teilt das Ganze durch die Summe der Gewichtsfaktoren. Im Beispiel hier ist das Ergebnis $$\mu=\frac{15.78\cdot 0.252+7.28\cdot 0.371+9.17\cdot 0.330+12.15\cdot 0.287+22.23\cdot 0.212 }{15.78059072+ 7.28323699+ 9.17012448+ 12.14656489+22.22981956}$$ und das ergibt den neuen RR-Schätzwert, nämlich RR=1.44. Man kann außerdem ableiten, welcher Standardfehler bzw. welches 95%-Vertrauensintervall nun wiederum dieser neue Schätzwert hat. Das rechne ich hier aber nicht vor (und rechne es auch nicht per Hand aus) sondern überlasse die Arbeit dem pythonMeta-Paket für Python. (Da Statistiker*innen soweit ich weiß häufiger R als Python nutzen, dürfte R auch das häufigere Werkzeug bei Meta-Analysen sein – und es gibt auch dieses schön verständliche Online-Buch dazu – aber ich bin Astrophysiker und bleibe zumindest in punkto Programmiersprache bei meinen Leisten.)

Hier ist die gesamte Ausgabe-Zusammenfassung des Pakets für meine fünf simulierten Studien:

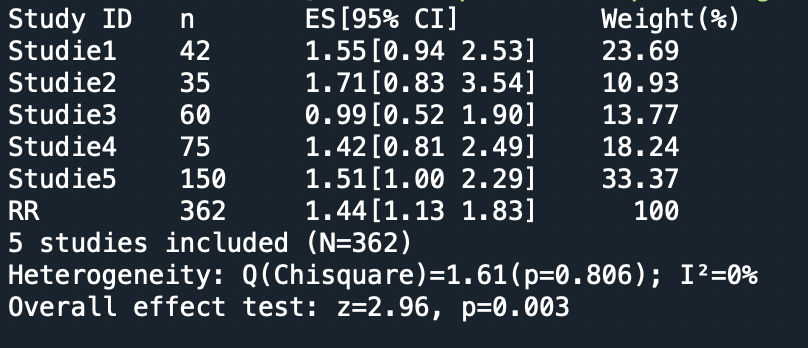Einiges davon kennen Sie schon. Einiges können Sie direkt verstehen – die Gewichts-Angabe “Weight” gibt an, wieviel die einzelnen Studien jeweils prozentual zum Gesamtergebnis beitragen. Das Gewicht wird nicht ganz nach Teilnehmerzahl vergeben, aber weit davon weg ist die Gewichtung auch nicht. Die 150-Teilnehmer-Studie beispielsweise leistet den größten Einzelbeitrag. Dass die erste Studie vergleichsweise viel beiträgt wird daran liegen, dass die Stichproben-induzierte Schwankung bei dieser Studie vergleichsweise klein ist.

In diesem Falle kennen wir, da es sich um eine Simulation handelt, den wahren Wert von RR, nämlich RR=1.429. Dem kommt der Schätzwert der Meta-Analyse tatsächlich näher als 4 der fünf Einzelstudien, und jene fünfte “gute” Einzelstudie hat natürlich ein deutlich größeres Vertrauensintervall. Die Meta-Analyse tut also, was sie soll: Die Daten der Einzelstudien zu einer besseren Schätzung – hohe Wahrscheinlichkeit den wahren Wert zu treffen, schmaleres Vertrauensintervall – zusammenzufassen. Last but not least: In der Meta-Analyse ist der Effekt dann tatsächlich signifikant: Der neutrale Wert RR=1 liegt deutlich außerhalb des kombinierten Vertrauensintervalls.

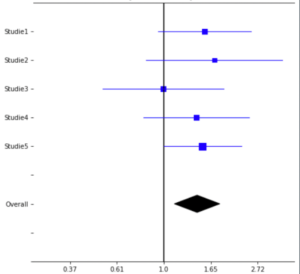
Typisch für Publikationen zu Meta-Analysen ist ein Wald-Diagramm (forest plot) wie dieses hier:

Auf der waagerechten Achse ist dabei die Effektstärke RR aufgetragen. Auf der senkrechten Achse sind erst eine unter der anderen die fünf Einzelstudien dargestellt, darunter in Diamantform das Ergebnis der Meta-Analyse. Für jede der Einzelstudien ist sowohl die RR-Schätzung als auch das 95%-Vertrauensintervall dargestellt. Dass das Vertrauensintervall, also die jeweilige blaue waagerechte Linie, die senkrechte Linie bei der neutralen Effektstärke RR=1.0 schneidet oder im Falle der Studie5 zumindest berührt, zeigt, dass der Effekt in keiner der Einzelstudien signifikant war. Die Breite des Diamants repräsentiert das 95%-Vertrauensintervall der Meta-Analyse. Dass es ein signifikantes Ergebnis ist kann man direkt daraus ablesen, dass der Diamant mit Zwischenraum rechts von der neutralen Linie RR=1 liegt.

Soweit, so gut. Man kann zumindest erahnen, was diese Art von Analyse zum “Goldstandard” z.B. der evidenzbasierten Medizin macht. Die Cochrane Collaboration ist an dieser Stelle ja Vorreiter, publiziert selbst eine große Menge an methodisch sehr gut gemachten Studien nach diesem Muster und liefert mit einem ausführlichen und gut lesbaren methodischen Handbuch eine sehr ausführliche Darlegung der zugrundeliegenden Methodik und damit auch der Standards solcher Reviews.

Meta-Analyse mit zufälligen Effekten

Mein simuliertes Beispiel war aber natürlich idealisiert. Das, was eine homogene Studienlage und damit die feste-Effekte-Meta-Analyse annehmen müssen damit diese einfache Art der Auswertung funktioniert, war in meiner Simulation per Definition gegeben. Ich habe meine “Studienergebnisse” zwar zufällig generiert, aber auf Basis derselben Wahrscheinlichkeiten – 0.5 Heilungswahrscheinlichkeit für die Experimentalgruppe, 0.35 Heilungswahrscheinlichkeit für die Kontrollgruppe – für jede der fünf Studien.

Im wirklichen Leben ist die Lage üblicherweise komplexer. Selbst wenn verschiedene Studien zu ein und demselben Effekt durchgeführt werden, ist zu erwarten, dass sich jene Studien nicht nur durch die Stichprobeneffekte unterscheiden, sondern außerdem durch systematische Effekte. Bei Medikamenten-Studien kann es beispielsweise sein, dass ein Krankenhaus auf die entsprechende Krankheit spezialisiert ist und deswegen im Schnitt kränkere Patient*innen mit jener Krankheit (nämlich insbesondere all die besonders schweren Fälle, die gerade wegen der besonderen Schwere den Weg zur Spezialklinik suchen) aufweist. Oder aber die Altersstruktur ist systematisch unterschiedlich: Ein Krankenhaus liegt in einer Gegend mit älterem Altersdurchschnitt als ein anderes, und entsprechend unterscheiden sich die wahren Wahrscheinlichkeit für eine Heilung mit und ohne Medikament. Auch im Design können sich die Studien natürlich unterscheiden. Vielleicht werden doch systematisch etwas unterschiedliche Dosierungen an die Experimentalgruppe gegeben. Vielleicht wird der Endpunkt – also die Beurteilung krank oder gesund – in der einen Studie nach einer Woche dokumentiert, in der anderen Studie nach zwei Wochen. Diese und weitere mögliche Effekte von Unterschieden nicht aufgrund der Stichprobenfehler sondern aufgrund systematischer Verschiedenheit führen zu einem heterogenen Datensatz – die Studien sind dann nicht unterschiedliche Messungen ein und desselben Effekts, sondern sie messen zwar noch ähnliche, aber letztlich verschiedene Effekte und damit auch verschiedene Effektstärken. Für solche Situationen gibt es Techniken für die Meta-Analyse mit zufälligen Effekten.

Das Grundprinzip ist dabei sehr ähnlich. Wieder bildet man einen gewichteten Mittelwert für die Effektstärke. Wieder sind die Gewichte so etwas wie die Kehrwerte von quadrierten Standardfehlern – mit anderen Woren, weil das Quadrat des Standardfehlers auch Varianz genannt wird: die Kehrwerte von Varianzen. Aber diesmal gibt es zwei Beiträge pro Einzelstudie. Bei der genannten Methode wird angenommen, dass die Effektstärken, die in den verschiedenen Studien gemessen werden, eben nicht dieselben sind, sondern ihrerseits aus einer Wahrscheinlichkeitsverteilung stammen. Wir haben es dann mit einer doppelten Schätzung zu tun: Jede einzelne Studie versucht, mit ihrer Stichprobe die zur Studie gehörige Effektstärke zu schätzen. Und die Meta-Analyse versucht, mit der systematischen Auswertung der Einzelstudien so etwas wie den Mittelwert und die Streuung der Verteilung der verschiedenen Effektstärken abzuschätzen. Die Gewichte, mit denen die Meta-Analyse die Effektstärken der Studien kombiniert, haben deswegen zwei Anteile: Einmal die Varianz der Einzelstudie, als Maß für die Stichprobeneffekte jener Studie – genau wie bei der feste-Effekte-Meta-Analyse. Hinzu kommt aber noch die Varianz, die Unterschiede zwischen den verschiedenen Studien parametrisiert. Die konkreten Umsetzungen der Meta-Analyse in einem Modell mit zufälligen Effekte unterscheiden sich dabei darin, wie der Zahlenwert für jene Varianz-zwischen-den-Studien abgeschätzt wird. Der Gewichtsfaktor für jede einzelne Studie ist dann nicht eins durch die Varianz-der-Studie zum Quadrat, sondern eins durch die Summe jenes Varianzquadrats (dessen Wert für die Einzelstudie spezifisch) und des Quadrats der Varianz-zwischen-den-Studien (für alle Studien einer bestimmten Meta-Analyse derselbe Wert).

Zwischen Repräsentativität und “Äpfel und Birnen”

Nicht nur Papier ist geduldig, sondern auch Mathematik. Bei einer Meta-Analyse mit zufälligen Effekten kann man beliebige Studienergebnisse zu relativen Risiken kombinieren, solange man jeweils Effektstärke und Standardfehler der Effektstärke (bzw. von deren Logarithmus) kennt. Ob das Ergebnis sinnvoll ist, ist damit allerdings noch nicht gesagt. Wie es in der R-Einführung auch geschrieben steht: “In Extremfällen kann sehr hohe Heterogenität bedeuten, dass die Studien nichts gemeinsam haben, und dass es keinen Sinn ergibt, den kombinierten Effekt überhaupt zu interpretieren.”

Es gibt durchaus wichtige Anwendungsfälle, in denen diese Art von Meta-Analyse einen echten Mehrwert liefert. Nehmen wir den Fall, dass die Altersverteilung der Teilnehmer*innen sich von Studie zu Studie systematisch unterscheidet. Falls die Studien in dem Sinne repräsentativ sind, als dass sie insgesamt, alle Teilnehmer*innen zusammengenommen, einigermaßen gut die Altersstruktur der Bevölkerung abbilden, dann ergibt die Meta-Analyse die über die verschiedenen Altersgruppen gemittelte Effektstärke – und das ist ja eine durchaus sinnvolle und interessante Information.

Schwieriger wird es bei Studien, die von vornherein deutlich unterschiedliche Effekte messen. Das sieht man besonders einfach, wenn es um mehrere jede für sich sehr gut gemachte Studien geht, also um Studien, deren jeweilige einzelne Stichprobeneffekte sehr klein sind (z.B. weil jede davon bereits eine sehr große Stichprobe umfasst). Liegen die unterschiedlichen Effekte, die gemessen werden, im Vergleich zu jenen individuellen Varianzen der Studien weit auseinander, dann dominiert die zwischen-den-Studien-Varianz die Gewichtung – und die ist ja für die Meta-Analyse insgesamt definiert. Das führt dazu, dass die gewichtete Mittelung in immer besser Näherung zu einem normalen Mittelwert wird. Und ein normaler Mittelwert zwischen sehr unterschiedlichen Größen ist zwar mathematisch definiert, ergibt aber nicht unbedingt Sinn und hat nicht unbedingt eine sinnvolle Interpretation. Der entscheidende Vorteil von Meta-Analysen, dass sie nämlich die Stichprobeneffekte vermindern, weil die Stichproben der einzelnen Studien in gewisser Weise zu einer großen Stichprobe kombiniert werden, fiele in dieser Situation ebenfalls weg.

Besonders heterogene Studien zusammenzufassen, die deutlich verschiedene Effekte messen, bringt damit potenziell mehrere Probleme mit sich: Der Schätzwert, der sich aus der Meta-Analyse ergibt, hat keine sinnvolle Interpretation mehr. Und die Vertrauensintervalle konvergieren nicht auf einen besten Schätzwert, sondern bleiben groß – und damit wird es allgemein schwieriger, für so einen heterogenen Schätzwert eine signifikante Effektstärke festzustellen. Das, was eine sinnvoll angelegte Meta-Analyse so wertvoll macht – ein sinnvoller Schätzwert, der besser ist als die Einzel-Schätzwerte, und der fast-wie-eine-große-Stichprobe-Vorteil – fällt damit potenziell weg.

Das Cochrane-Handbuch (gegen Ende von Abschnitt 10.10.1) drückt es so aus: “Meta-Analyse sollte nur in Betracht gezogen werden, wenn eine Gruppe von Studien in Bezug auf Teilnehmer*innen, Interventionen und Endpunkte so hinreichend homogen ist, dass eine Zusammenfassung sinnvoll ist. Es ist dabei oft angemessen, in einer Meta-Analyse eine breitere Perspektive einzunehmen als in einer einzelnen klinischen Studie. Eine häufige Analyse ist dass systematische Reviews Äpfel und Birnen zusammenbringen, und dass eine Kombination aus den beiden zu einem sinnlosen Resultat führen kann. Das ist wahr, wenn Äpfel und Birnen jeweils für sich interessant sind, aber es kann auch unwahr sein, nämlich dann wenn die beiden genutzt werden, um eine allgemeinere Frage über Früchte zu beantworten.” Das ist entsprechend die Bandbreite, mit der wir es bei Meta-Analysen zu tun haben. Von homogenen Gruppen von Studien, in denen die Meta-Analyse die Stichprobenfehler reduzieren kann, über heterogene Gruppen die Teil einer breiteren Verteilung von Effekt-Variationen sind die mit dem Mittelwert, der sich aus der Meta-Analyse ergibt, sinnvoll charakterisiert werden können, bis hin zu echten Äpfel-Birnen-Situationen, in denen inhaltlich überhaupt nicht klar ist, was der Mittelwert und sein Vertrauensintervall nun eigentlich bedeuten sollen.

Anmerkung zu den Kommentaren
In Anbetracht früherer Erfahrungen hier auf diesem Blog gilt nach wie vor: Alle Kommentare in diesem Blog sind moderiert, und ich werde nur Kommentare freischalten, die sich direkt auf das Thema dieses Blogbeitrages beziehen und die keine Beleidigungen enthalten. Es gibt genügend allgemeine Foren für Diskussionen; direkt hier bei diesem Blogbeitrag möchte ich die Diskussion auf das Beitragsthema einschränken.