Ein kritischer Blick auf die globale Temperaturentwicklung
BLOG: RELATIV EINFACH

Der Klimawandel ist – im Gegensatz zu Astronomie/Astrophysik,Relativitätstheorie(n) oder, allgemeiner, Wissenschaft und Öffentlichkeit – kein Thema, mit dem ich mich beruflich beschäftige. Aber weil die Einschätzungen zum Klimawandel in unserer Gesellschaft (weniger in der Wissenschaft selbst) ja ziemlich drastisch auseinandergehen, habe ich mir vorgenommen, an einigen ausgewählten Stellen selbst nachzuhaken, und zumindest Teilaussagen selbst nachvollziehen und auf ihre Konsistenz hin prüfen (erstmals vor knapp zwei Jahren in Rahmstorf im Zerrspiegel und Meichsner vs. Rahmstorf Teil II: Dürre in Afrika).
Neulich bin ich mit dem KlimaLounge-Beitrag Globale Temperatur 2012 (und dem verwandten Beitrag von 2009 Macht die Erderwärmung Pause?) wieder auf einen Aspekt gestoßen, der mir zum Nachprüfen geeignet scheint, nämlich die Frage, ob die Temperaturkurve der letzten Jahre Behauptungen wie jene, der Klimawandel habe für die letzten 15 Jahre eine Pause eingelegt, stützt oder nicht.
Rahmstorf spricht von “sinnlose[n] Debatten über einen angeblichen Stillstand der Erderwärmung” “[i]m Netz und einigen Medien”. Im SPIEGEL dagegen, um ein Beispiel zu nennen, ist “die Pause beim Temperaturanstieg in den letzten 15 Jahren”, wie jüngst hier, eine häufig wiederholte Formulierung, ohne Hinweise, dass dies irgendetwas anderes als Konsens sein könnte. Von dort habe ich mich auf diesen SPIEGEL-Artikel hier durchgeklickt und den als Anlass genommen, selbst nachzuschauen, was es mit den Temperaturkurven auf sich hat.
Die Temperaturdaten
Der letztgenannte SPIEGEL-Artikel hatte als Aufhänger die Veröffentlichung der (damals) jüngsten NASA-Daten für die Temperaturkurve. Genauer: in dieser Kurve geht es um die globalen Mittelwerte für die Temperatur nahe der Erdoberfläche (Land und Ozean). Die entsprechenden NASA-Daten sind (zumindest zu den Zeiten, wo die USA einen funktionierenden Staatsapparat haben), hier abrufbar und werden in dieser Pressemitteilung beschrieben. Außer dem SPIEGEL hat sich noch Stefan Rahmstorf in der KlimaLounge hier dazu geäußert. Das ist mein Ausgangsmaterial.
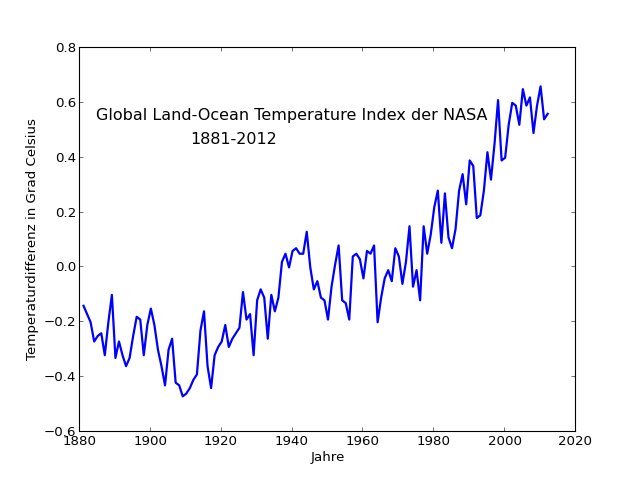
Ich habe eine Version der Textdatei, die ich minimal verändert habe (Kommentarzeichen # vor den Nicht-Daten-Zeilen und dem unvollständigen Eintrag für 1880 eingefügt) hier als GLB.Ts+dSST-v2 abgelegt. Wenn wir diese Daten einfach nur plotten, für jedes Jahr die mittlere Temperatur in diesem Jahr, sieht das so aus:
Das Python-Skript, mit dem ich den Plot erzeugt habe, habe ich hier abgespeichert (es benutzt hauptsächlich matplotlib). Die Daten sind Differenzen zu einem in der Datei nicht explizit angegebenem Bezugspunkt, keine Absoluttemperaturen.
Bereits nach der Begutachtung mit bloßem Auge liegt nahe: Wir haben es mit längerfristigen Entwicklungen zu tun, die von kürzerfristigen Schwankungen überlagert sind. Die längerfristigen Entwicklungen, nach Augenmaß: ein flaches Tal zwischen 1880 und 1935, dann von etwa 1950 bis 1965 eher so etwas wie Stagnation, und von ungefähr 1965 an geht es dann recht gerade nach oben – auf das letzte Stück gehe ich gleich noch deutlich genauer ein.
Längerfristige Trends sichtbar machen
Angesichts solcher Daten stellt sich sofort die Frage: Wie kann man die längerfristigen Trends von den kurzfristigen Schwankungen trennen?
In der Sprache der Signalverarbeitung brauchen wir so etwas wie einen “Tiefpass”, der nur langsame, “niederfrequente” Veränderungen durchlässt und schnellere, “höherfrequente” Veränderungen herausfiltert. Ich habe Stefan Rahmstorf per E-mail gefragt, wie er denn die geglättete Kurve in seiner Grafik (Abb. 1 hier) erzeugt hat. Seine Antwort war, es handle sich um das SSATrend-Filter, das in Moore et al. 2011 beschrieben werde, aber auch mit dem LOWESS-Verfahren gebe es ähnliche Ergebnisse.
Ich habe mir die entsprechenden Artikel angeschaut (allerdings nicht richtig durchgearbeitet) und möchte es erst einmal mit einfacheren Mitteln versuchen – nicht zuletzt, weil es mir in diesem Blogbeitrag um diejenigen Aussagen geht, die man auch ohne größere Vorkenntnisse nachvollziehen und testen kann. Ich bin mir des Umstands bewusst, dass so eine Vereinfachungsstrategie für einige wissenschaftliche Fragestellungen nicht funktioniert. Manchmal kommt man nicht umhin, komplexere Werkzeuge zu benutzen. Aber schauen wir erst einmal, was in diesem Falle herauskommt.
Die direkteste Methode, um Trends sichtbar zu machen und Schwankungen zu unterdrücken, ist die Bildung von Mittelwerten. Dabei heben sich, je nach gewählter Zeitskala, die kurzfristigeren Schwankungen einigermaßen heraus. Ich verwendete gleitende Mittelwerte, das heißt: Für ein Mittelwert-Intervall von 3 Jahren trage ich beim x-Achsen-Wert des Jahres T den Mittelwert der Jahre T-1, T und T+1 (also insgesamt 3 Jahre) auf. Bei einem Mittelwert-Intervall von 5 Jahren den Mittelwert der Jahre T-2, T-1, T, T+1, T+2, und so weiter.
Die erste Frage ist dann, über welchen Zeitraum wir am besten mitteln. Im folgenden beginne ich bei den niedrigsten möglichen Werten: 3 Jahre, 5 Jahre und so weiter. Ich schaue dann jeweils auf die Kurve und schätze nach Augenmaß, welchen Einfluss die Mittelung auf die kürzerfristigen Hin-und-Her-Schwankungen hat. Sind die Schwankungen so gut wie verschwunden, dürfte die gemittelte Kurve den Trend gut wiedergeben.
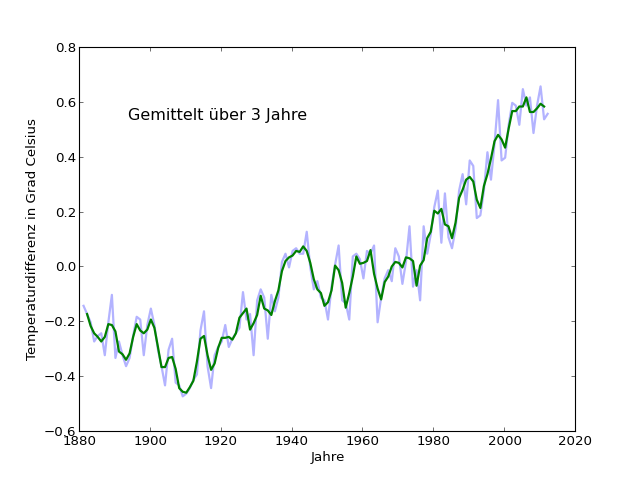
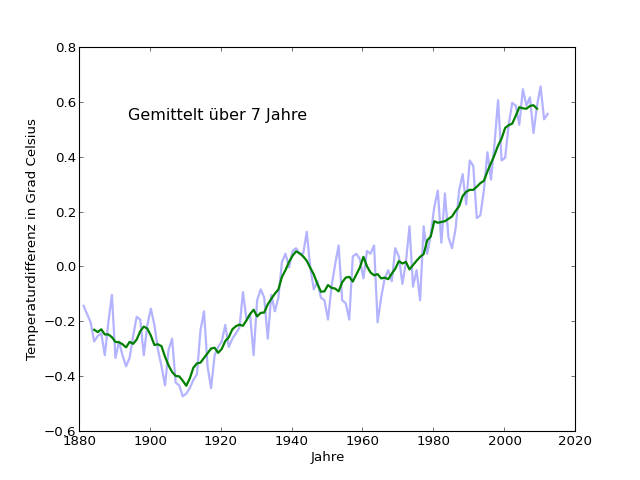
Die folgenden Abbildungen zeigen jeweils die Originaldaten (ungemittelt) in hellblau und die gemittelte Kurve in grün. Die Abbildungen habe ich wieder mit einem Python-Skript [averaged-t-plots] erzeugt. Fangen wir mit dem kleinsten Mittelwert-Intervall an, 3 Jahren:
Der Endwert bei 2011 ist nach wie vor niedriger als bei den Jahren zuvor, aber ähnliche Phasen ohne klare lokale Steigung gibt es in der im Trend ansteigenden Kurve (ab etwa 1970) noch einige weitere – 1980 bis 1986 etwa, oder 1987 bis 1993.
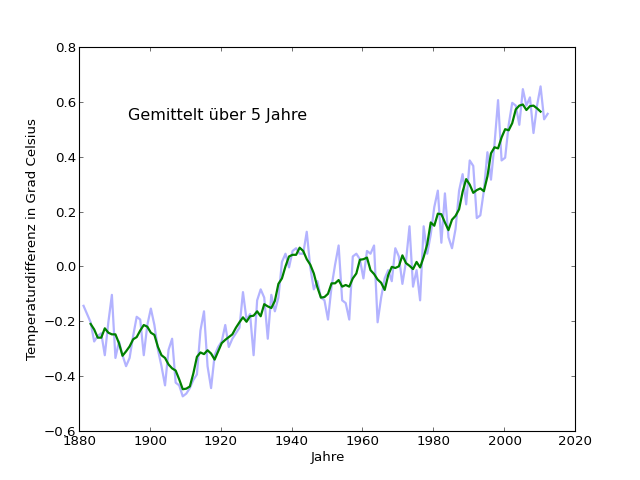
Außerdem ist deutlich zu sehen, dass das Zeitintervall von 3 Jahren noch nicht lang genug ist, um die kurzfristigen Schwankungen auszugleichen. Das kürzerfristige Auf und Ab fällt zwar bereits etwas weniger ins Gewicht, beeinflusst aber den Verlauf noch ganz deutlich auf ähnlichen Zeitskalen wie vorher. Mitteln wir als nächstes über 5 Jahre:
Ein ähnliches Bild. Weiterhin ein Abknicken am Ende der Kurve (jetzt 2005 bis 2010), das sich allerdings nicht sonderlich von ähnlichen Schlenkern vorher (z.B. 1989 bis 1994) unterscheidet. Immer noch ist das Auf und Ab der kürzerfristigen Veränderungen sichtbar – um dem längerfristigen Trend auf die Spur zu kommen, schaue ich mir daher als nächstes das 7-Jahres-Mittel an:
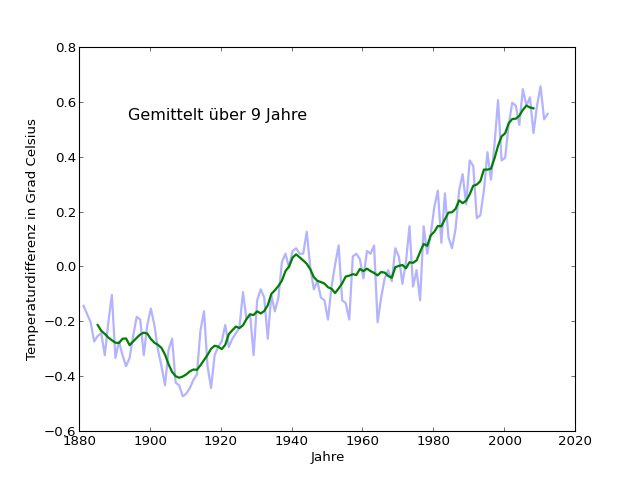
Wieder ein weiter abgeschwächter Endschlenker ähnlich früheren Schlenkern (z.B. 1969-1974), und immer noch deutliche Überreste der kurzfristigen Schwankungen. Also, 9 Jahre:
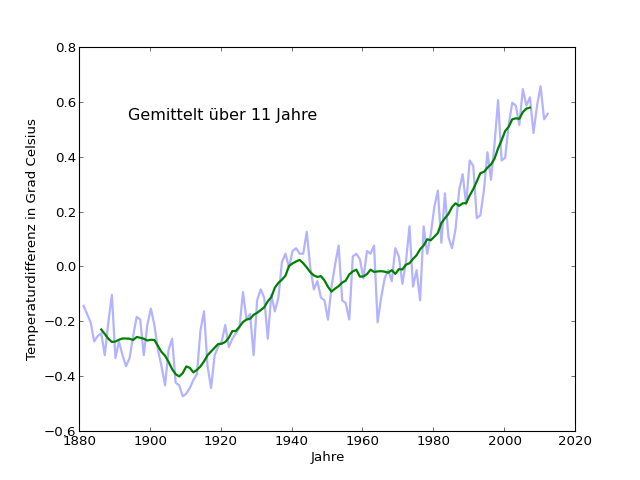
Wieder etwas glätter, aber nach wie vor deutliches hin und her. Die Abflachung am Ende ist noch unauffälliger geworden und betrifft nur noch die letzten zwei erfassten Jahre. 11 Jahre Mittelungszeitraum:
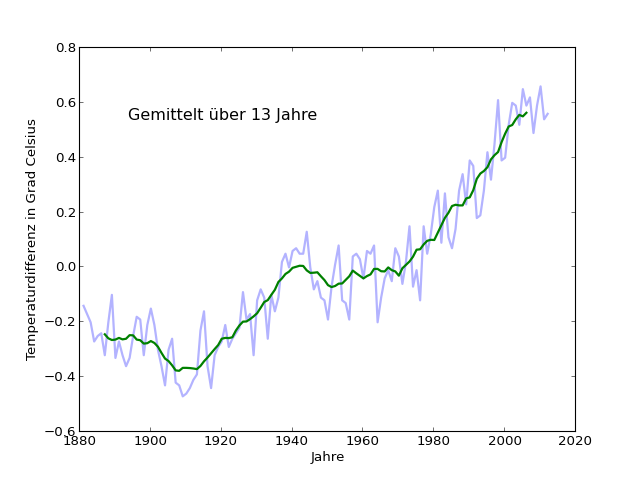
Etwas Zittern ist um die Trendkurve herum noch geblieben. Aber es bildet nicht mehr direkt das Zittern der blauen Hintergrundkurve ab. Noch etwas länger?
Zumindest dem Augenschein nach keine große Verbesserung gegenüber den 11 Jahren. Noch zwei Schritte weiter?
An dieser Stelle könnte man noch weiter mitteln, aber ich höre hier erst einmal auf.
Ein genauerer Blick auf die Schwankungen
Die Kurven mit gleitendem Mittel haben einen Nachteil. So, wie ich sie aufgetragen habe – der Punkt für das Jahr X entspricht dem Mittelwert der Temperaturwerte des Jahres X und der Jahre darum herum, insgesamt N Jahre – kommt man zwangsläufig nicht ganz bis zum Ende der Datenreihe. Kann es sein, dass wir so am Ende etwas verpassen? Eben zum Beispiel das Abknicken?
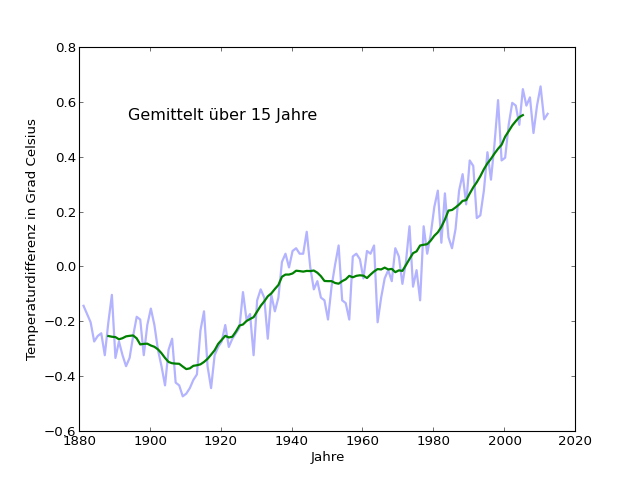
Dass wir bei den oben gewählten Mittelungsintervallen keine 10 oder gar 15 Jahre Stillstand des Erwärmungstrends verpassen, ist deutlich sichtbar. Selbst beim 15-Jahres-Mittel bekommen wir Werte bis 2005 (wie gesagt: zum Anzeigen wählen wir immer das Jahr in der Mitte des Intervalls).
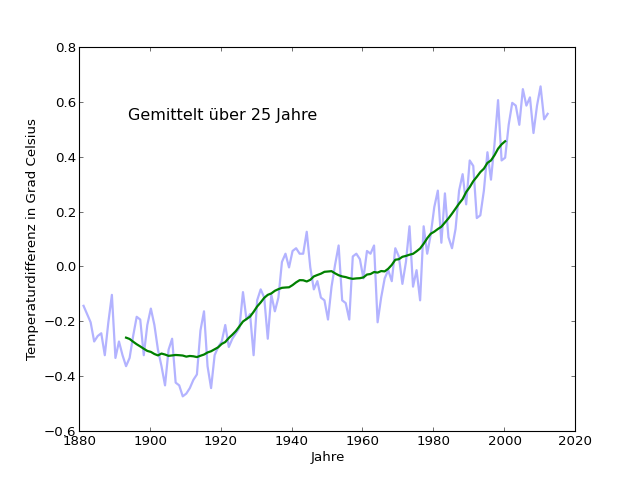
Aber ich möchte noch einen weiteren Test machen und die letzten 15 Jahre direkt mit der Anstiegsphase ab 1980 vergleichen. Dazu benutze ich jetzt ein noch längeres Mittelungsintervall, nämlich über 25 Jahre. Das sieht so aus:
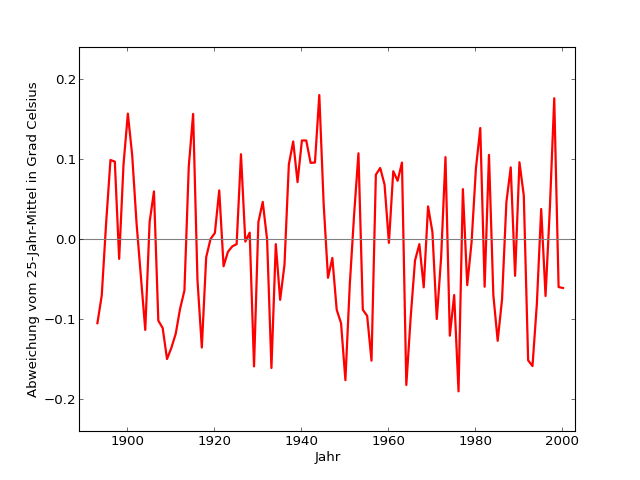
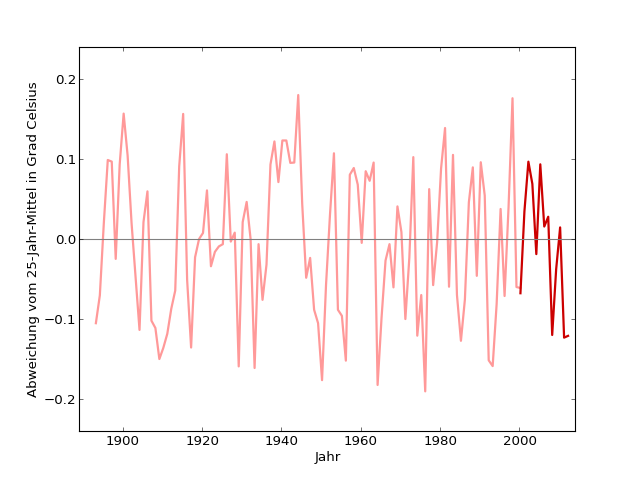
Jetzt betrachte ich für den Jahresbereich, in dem ich Mittelwertdaten habe, also 1893 bis 2000, die Abweichungen des jeweiligen Jahreswerts vom um dieses Jahr zentrierten 25-Jahre-Mittelwert. Das ist so etwas wie das Gegenstück der gemittelten Kurve, die ja den längerfristigen Trend sichtbarer gemacht und die Schwankungen unterdrückt hat (grüne Kurve), nämlich umgekehrt eine Kurve, die fast nur noch die Schwankungen enthalten sollte [extract-short-term]:
Diese Abweichungen können als Vergleich dienen, um zu beurteilen, wie stark die letzten 15 Jahre – also das Zeitintervall, von dem wir prüfen wollen, ob dort alles anders war – von den Jahren davor abweicht.
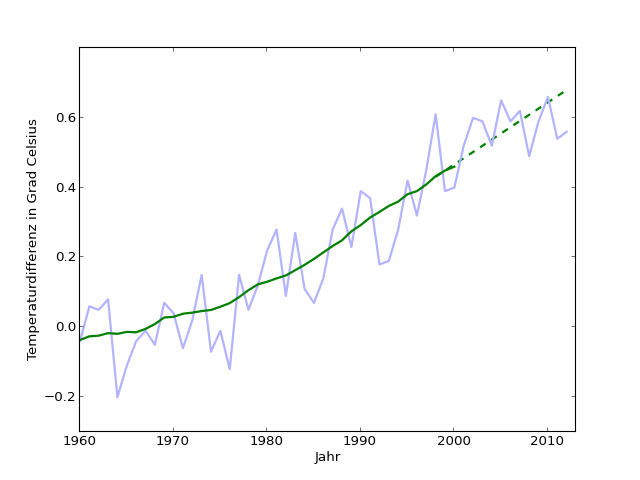
Dazu mache ich folgendes: Ich nähere einen Teil der 25-Jahre-Mittelwert-Trendkurve (1982 bis 2000), der ziemlich gerade aussieht, durch eine Gerade an. Dafür gibt es ein gängiges mathematisches Verfahren (lineare Regression). Diese Gerade setze ich dann über 2000 hinaus fort. Im folgenden Diagramm [Python-Programm extrapolate-last-bit.py] ist die Fortsetzung gestrichelt eingezeichnet:
Als nächstes vergleiche ich die Abweichungen von den Trendkurven für den Zeitraum 1893 bis 2000 (dafür habe ich ja die 25-Jahres-Trendkurve erstellt) und für den Zeitraum 2001-2012 (da nehme ich als Bezugslinie die Fortsetzung der Gerade). Wären die Abweichungen im zweiten Zeitraum deutlich stärker, wäre das ein Hinweis darauf, dass meine Extrapolation an der Wirklichkeit vorbeigeht.
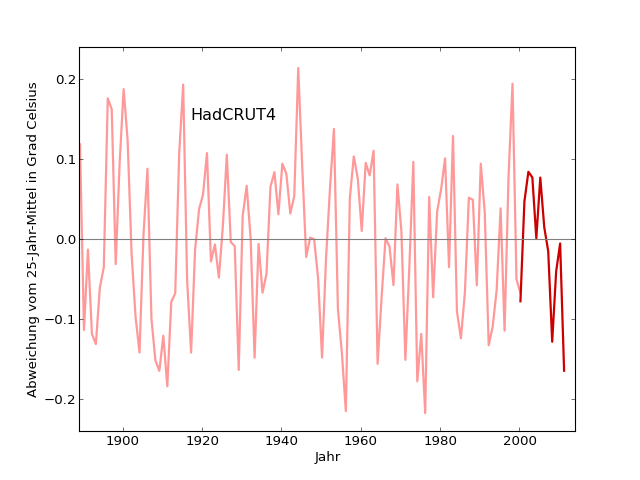
Hier ist erst einmal die grafische Darstellung [Python-Programm abweichungen-alle]. Die Abweichungen (von der 25-Jahre-Mittelungskurve) von 1893 bis 2000 sind hellrot, die Abweichungen 2001-2012 (von der Extrapolationskurve) dunkler:
Schon mit bloßem Auge sieht man, dass die Abweichungen bei der Extrapolationskurve sogar eher geringer sind als die Abweichungen von der 25-Jahre-Mittelwertkurve in den Jahren davor.
Zur Sicherheit versuche ich’s nochmal quantitativ. Der Mittelwert der Schwankungen von 1893 bis 2000 ist -0,006 Grad Celsius. Dass dieser Wert nahe bei Null liegt, ist ein gutes Zeichen; wenn in dem, was ich hier Schwankungen nenne, noch ein deutlicher Trend nach oben oder unten enthalten wäre, würde sich der Mittelwert der Schwankungen merklich von Null entfernen. Für die Stärke der Schwankungen (grob gesprochen: wieweit geht’s typischerweise nach oben/unten?) gibt es in der beschreibenden Statistik als Maß die (korrigierte) Stichprobenvarianz. Hier beträgt sie 0,092 Grad Celsius.
Könnten die unterschiedlichen Messgenauigkeiten (zu erwarten wäre: die frühen Messungen sind weniger genau als heute) hier einen störenden Einfluss haben? Zur Sicherheit betrachte ich die Jahre von 1982 bis 2000 gesondert. Dort ist der Mittelwert -0,016 Grad Celsius, also deutlich größer, aber immer noch recht klein. Die Stichprobenvarianz ist 0,095 Grad Celsius; hier sind die Abweichungen von der Trendkurve also sogar noch etwas größer als im Gesamtzeitraum meiner 25-Jahre-Mittelung.
Jetzt zur Extrapolation: Für meine Abweichungen von der extrapolierten Kurve ist der Mittelwert der Abweichungen -0,009 Grad Celsius; wiederum ein gutes Zeichen dafür, dass meine Extrapolationsgerade den Trend wiedergibt, um den die Schwankungen symmetrisch streuen. Die Stichprobenvarianz beträgt nun 0,079 Grad Celsius, ist also in der Tat kleiner als in den vorigen Fällen.
Dieser Test liefert demnach keinen Hinweis darauf, dass die extrapolierte Kurve die langfristige Entwicklung schlechter beschreiben würde als es die 25-Jahre-Trendkurve tut.
Welche Daten?
Allles, was ich bislang argumentiert habe, bezog sich direkt auf die NASA-Daten, deren Datenpunkt für 2012 Anlass sowohl des zitierten Spiegel-Artikels als auch des Rahmstorf-Beitrags war. Aber es gibt noch andere Datenreihen – der Spiegelartikel verlinkt z.B. auf diese Seite der Britischen Wetterbehörde, in der (die entsprechende Abbildung hat der Spiegel-Artikel auch als Aufhänger) Beobachtungskurven von Hadley Centre, GISS und NCDC zusammengefasst werden – auf dieser Seite hier steht genaueres: “The three international global temperature data sets are from the Met Office and University of East Anglia (HadCRUT3), NOAA National Climatic Data Center (NOAA NCDC) and NASA Goddard Institute of Space Studies (NASA GISS).” In dem von Rahmstorfs Blogbeitrag aus verlinkten Artikel Foster & Rahmstorf 2011 werden die gleichen Datensätze benutzt.
Zusätzlich gibt es noch das Projekt von Wissenschaftlern um den Physikprofessor Richard Muller, Berkeley Earth, das sich – durchaus (auch) durch Skepsis gegenüber den herkömmlichen Klimaforschern motiviert – daran gemacht hat, eigene mittlere Temperaturen und -differenzen zu ermitteln.
Unterscheiden sich die Schlüsse, je nachdem, welchen Datensatz man zugrundelegt?
Die NOAA-NCDC-Daten sind, soweit ich sehen kann, diese hier. Beim Mitteln zeigen sie die gleichen Eigenschaften wie die NASA-Daten; ab einem Mitteln über 11 Jahre ist das Abknicken am Ende verschwunden (3 Jahre, 5 Jahre, 7 Jahre, 9 Jahre, 11 Jahre [averaged-t-plots-NOAA]).
Die Berkeley-Daten sind von dieser Seite aus herunterladbar, die Datei ist diese hier. Die Daten sind (1) nur für den Landanteil der Erde (weil es dort die meisten Stationen gebe, argumentieren Muller et al.) und (2) in der Datei nach Monaten aufgeschlüsselt. Ich habe demnach zuerst die Jahresmittel gebildet. Das Ergebnis ist qualitativ das gleiche wie bei NASA und NOAA: ein Abknicken, das ab einem Mitteln über 11 Jahre verschwunden ist (3 Jahre, 5 Jahre, 7 Jahre, 9 Jahre, 11 Jahre [averaged-t-plots-BE]).
Die HadCRUT-Daten sind hier zum Herunterladen verfügbar; inzwischen gibt es nach HadCRUT3 auch HadCRUT4. Die Datensätze dafür sind hier (3) und hier (4). Vom Format her gibt es diesmal zwei Zeilen pro Jahr; in der jeweils ersten Zeile sind die Temperaturanomalien für die 12 Monate des Jahres und dann noch das Jahresmittel. Die zweite Zeile gibt an, welchen Anteil (in Prozent) der Erdoberfläche die Daten abdecken – das liegt in den letzten Jahren bei um die 80% oder besser, um 1900 bei etwa der Hälfte. Hier (3) und hier (4) habe ich Versionen gespeichert, in denen ich jeweils diese zweite Zeile pro Jahr entfernt habe, um die Daten mit meinem Plotting-Skript einfacher auslesen zu können.
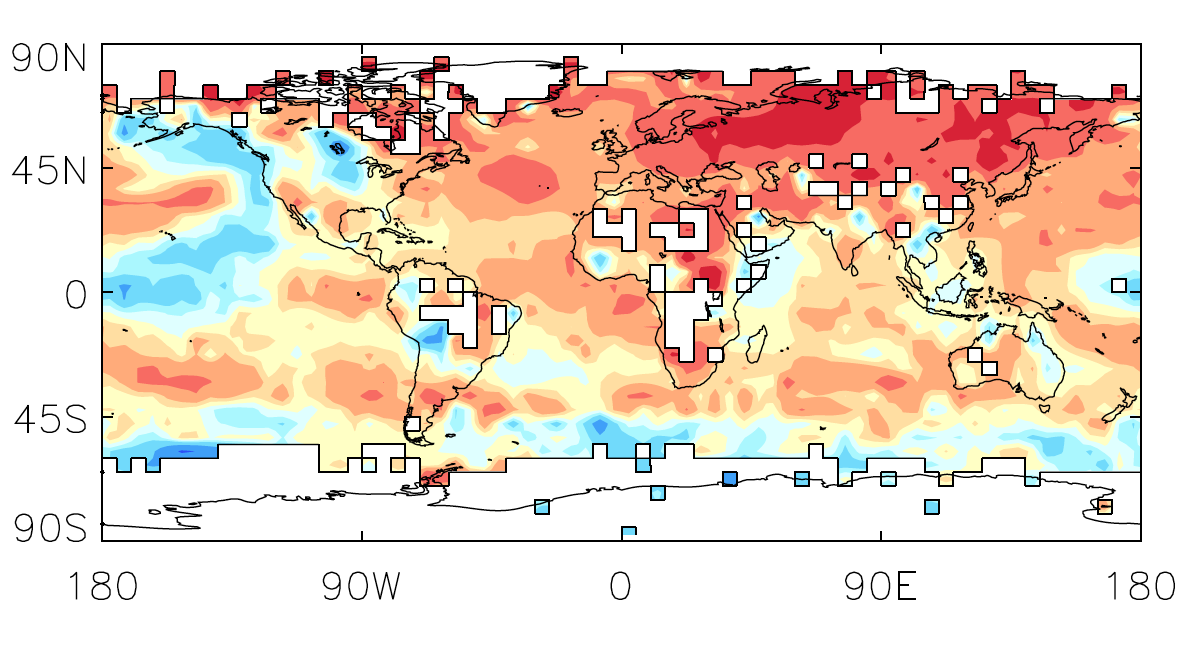
Eine Besonderheit von HadCRUT ist (z.B. S. 3 in Morice et al. 2012), dass kein Versuch gemacht wird, die gemessenen Temperaturwerte auf die gesamte Erde hochzurechnen, in dem folgenden Sinne: HadCRUT teilt die Erdoberfläche, grob gesprochen, in gleich große Felder auf. Liegt in oder nahe einem der Felder eine Meßstation, dann trägt deren Temperaturwert zum Durchschnitts-Temperaturwert für das betreffende Feld bei. Für Felder ohne hinreichend nahe Meßstation werden keine Temperaturwerte ermittelt. Die folgende Grafik aus Morice et al. 2012 (Ausschnitt aus Fig. 4) dürfte repräsentativ für den Abdeckungsgrad sein:
Ziemlich offensichtlich ist: Weitgehende Teile der Arktis und so gut wie die gesamte Antarktis werden von diesem Datensatz nicht erfasst. Das ist einerseits methodisch interessant, denn die Unterschiede zu den anderen Temperaturdaten geben dann (zumindest zum Teil) wieder, welcher Teil der Abschätzung der globalen Temperatur auf Interpolation beruht (sprich: dem Versuch, Abschätzungen für diejenigen Gebiete vorzunehmen, für die keine direkten Temperaturdaten zur Verfügung stehen). Der Verzicht auf Interpolation bedeutet aber auch, dass man HadCRUT-Kurven nicht einfach pauschal als “globale Temperaturentwicklung” werten darf. Rahmstorf ist auf das entsprechende “Arktisloch” u.a. hier eingegangen.
Die HadCRUT3-Reihe hat 1998 einen noch höheren Peak als die anderen Temperaturreihen. Das macht die Mittelwertkurven rund um 1998 konkaver als bei den anderen Datenreihen. Etwas von dem Abknicken, mit Höchstwert 2006, ist in der HadCRUT3-Reihe auch noch in der 11-Jahres-Mittelwertkurve zu sehen:
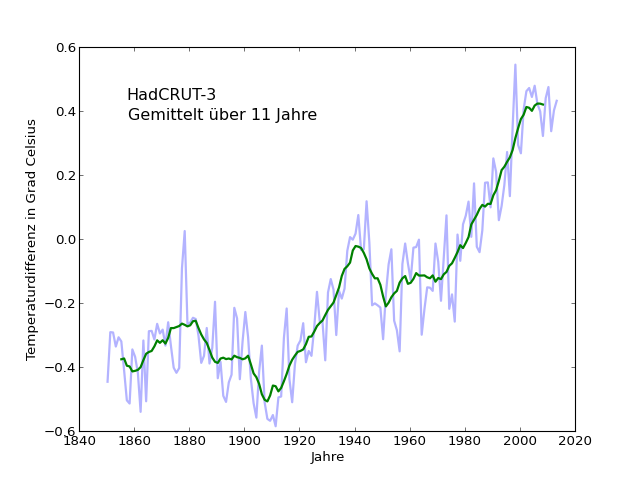
Generell zeigt aber auch dieser Datensatz das gleiche Verhalten: Sobald man mittelt, nähert sich die Kurve einem Aufwärtstrend an, und zwar umso stärker, je größer der Zeitraum der Mittelung ist (3 Jahre, 5 Jahre, 7 Jahre, 9 Jahre, 11 Jahre [averaged-t-plots-HadCRUT]).
Der Unterschied zwischen HadCRUT3 und HadCRUT4 wird in diesem Artikel hier, Morice et al. 2012 beschrieben. Unter anderem sind von 3 auf 4 125 arktische Stationen dazugekommen, so dass die Abdeckung in diesem Bereich nun besser ist als zuvor.
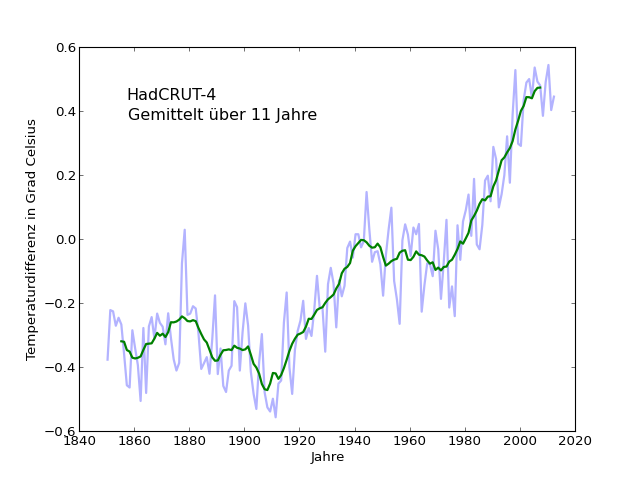
Damit sieht die 11-Jahres-Mittelwertkurve auch bei HadCRUT so aus wie bei den anderen Temperaturreihen:
Auch die Entwicklung beim Übergang zu immer längeren Mittelwerten ist wiederum der gleiche wie vorher: Ausschläge entsprechend den kürzerfristigen Trends, die immer geringer werden, je länger man mittelt; je länger man mittelt, umso mehr verschwindet das “Abknicken” am Ende (3 Jahre, 5 Jahre, 7 Jahre, 9 Jahre, 11 Jahre).
Wie sieht es mit dem Vergleich mit der Extrapolations-Geraden aus – insbesondere für die HadCRUT-Datensätze, die in den letzten 15 Jahren ja offenbar noch am ehesten von den NASA-Daten abweichen?
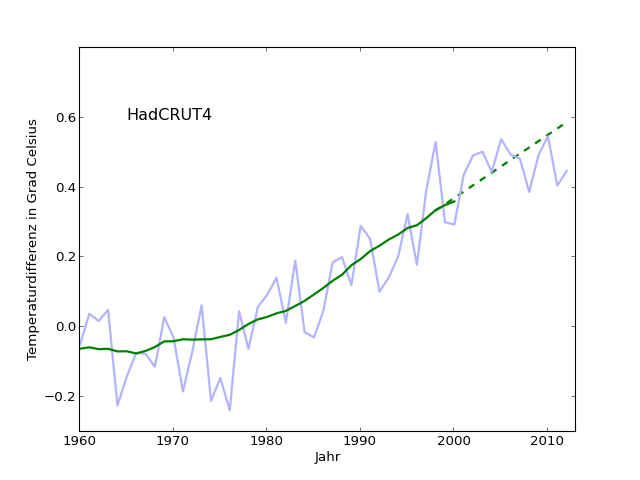
Hier ist die oben für die NASA-Daten beschriebene Extrapolationsgerade (basierend auf einer an 1982-2000 angepassten Geraden) für HadCRUT4 [extrapolate-last-bit-HadCRUT]:
Zumindest mit bloßem Auge könnte das eine Abflachung sein – im ersten Teil der Extrapolationsgerade liegt die blaue Kurve eher über der Extrapolationsgeraden, im zweiten Teil eher darunter. Andererseits: genau solch eine Behauptung könnte man z.B. auch für die Jahre 1977 bis 1986 aufstellen. Wie sieht es quantitativ aus? Hier sind wieder die Abweichungen von 25-Jahres-Durchschnitt (blassrot) vs. Abweichungen 2000-2012 von der Extrapolationskurve (rot) aufgetragen [abweichungen-alle-HadCRUT]:
Der Mittelwert der Abweichungen liegt von 1982 bis 2000 bei -0.012 Grad Celsius (mit den NASA-Daten waren es -0.016), also immer noch recht nahe an Null. Für den Extrapolationszeitraum sind es -0.010 Grad Celsius, also noch näher an Null (bei den NASA-Daten waren es -0,009 Grad Celsius). Die Standardabweichung der Abweichungskurve lag von 1982 bis 2000 bei 0,094 Grad, für die Extrapolationskurve bei 0,081 Grad. Wieder gilt also: Die Temperaturkurve 2000 bis 2012 weicht nicht stärker vom linearen Trend der vorangegangenen Jahrzehnte ab als in den Jahrzehnten davor. Auch hier keine Anzeichen für eine Trendwende.
Für HadCRUT3 bekomme ich im wesentlichen dieselben Ergebnisse (Abweichungs-Plot; Durchschnitt Abweichungen 1982-2000: -0,005 Grad Celsius, 2001-2012: -0,011 Grad Celsius; Standardabweichung Abweichungen 1982-2000: 0,100 Grad Celsius, 2001-2012: 0,088 Grad Celsius).
Wie beschreibt man eine solche Kurve?
Wie fasst man die Aussagen dieser Kurven sprachlich zusammen?
Allgemeinverständliche Sprache, wie sie in populärwissenschaftlichen Artikeln gefragt ist, hat notwendigerweise Unschärfen – das kennt jeder, der jemals entsprechende Texte geschrieben hat. Ich bin auch schon in solche Formulierungsfallen getappt. Wenn ich mir im folgenden die Formulierungen aus dem SPIEGEL-Artikel Klimawandel: Forscher rätseln über Stillstand bei Erderwärmung anschaue, dessen Anlass die damals (Januar 2013) ganz frischen NASA-Temperaturdaten sind, dann durchaus in dem Bewusstsein, dass es nicht einfach ist, immer eine ganz richtige Formulierung zu finden.
Allerdings ist mein Eindruck, dass die Missverständlichkeit einer Reihe der Formulierungen des Artikels weit über den unvermeidlichen Unschärfebereich herausgeht.
Das fängt bei der Überschrift an, die ja vom “Stillstand bei [der] Erderwärmung” redet. Damit ist doch offenbar ein längerfristiger Trend gemeint, denn auf Jahres- und Monatsebene ist das rasche Auf- und Ab ja nicht zu übersehen (der SPIEGEL-Webseitentitel “Stillstand der Temperatur” ist wohl nur eine missverständliche Verkürzung, wie er vorkommen kann, wenn jemand anderes als der Artikelautor die Überschriften formuliert).
Wie ist es damit oder mit der präziseren Aussage, “der Aufwärtstrend der globalen Durchschnittstemperatur hat sich seit 1998 nicht fortgesetzt”? Diese Aussage ist meiner Lesart nach die Kernbehauptung des entsprechenden SPIEGEL-Artikels.
Wie gesagt: Wenn wir den Trend von den kurzfristigen Veränderungen unterscheiden wollen, müssen wir mitteln oder anderweitig glätten. Das habe ich oben getan, und das Ergebnis war eindeutig: Der verbleibende Abwärtsschlenker am Ende wird immer unwichtiger, hat jeweils die gleichen Eigenschaften wie z.B. Abwärtsschlenker in dem ansonsten ansteigenden Stück, und ist bei der Mittelung über 11 Jahre oder länger, bei denen die kurzfristigen Schwankungen so gut wie eliminiert sind, ebenfalls verschwunden.
Bei der 11-Jahre-Mittelung setzt sich der langfristige Aufwärtstrend bis zum letzten Jahr fort, für das wir den Mittelwert errechnen konnte, nämlich bis 2007. Bei den weniger langfristigen Mittelungen, in denen die kurzfristigen Schwankungen noch deutlich sichtbar sind, bis 2004 (gemittelt über 7 Jahre), 2005 (über 5 Jahre) und 2006 (über 3 Jahre). Sobald man auch nur irgendwie anfängt zu mitteln, ist es nix mehr mit dem angeblichen Stillstand seit 15 Jahren.
Sind die Daten der letzten Jahre vereinbar mit einer Fortsetzung des Trends? Dazu hatte ich den ziemlich geraden Anstieg 1982-2000 (25-Jahres-Mittelung) als Gerade extrapoliert. Diese Gerade entspricht einem Trend, der unvermindert weitergeht. Dann hatte ich geschaut, ob die Jahresdaten für die Jahre 2001-2012 von der Anstiegsgeraden stärker abweichen als die vorangehenden Daten von der Trendkurve. Das wäre ein deutliches Zeichen gewesen, dass man den langfristigen Trend eben nicht einfach so fortschreiben darf. Aber die Abweichung der neueren Daten von der Trendkurve sind im Gegenteil noch kleiner als die typischen Abweichungen der Jahrzehnte davor.
Ich sehe demnach in den hier durchgeführten Tests keine Anzeichen dafür, dass der längerfristige Erwärmungstrend sich in den letzten 15 Jahren irgendwie verändert hätte.
Fazit und Ausblick
Was ich hier gemacht habe, ist kein Ausdruck spezialisierten Könnens. Man muss kein Klimaexperte dazu sein und auch kein data scientist oder Statistiker. Ich habe einfache Werkzeuge angewandt, die jeder Wissenschaftler und jede Wissenschaftlerin kennt, der/die irgendwie quantitativ mit Daten arbeitet: zeitliche Mittelung, um kurzfristige Schwankungen herauszurechnen; Ausgleichsgeraden; Mittelwerte und Stichprobenvarianz. Diese Methoden gehören zur wissenschaftlichen Allgemeinbildung – “allgemein” auch in dem Sinne, dass sie sich auf alle quantitativen Wissenschaften übertragen lassen.
Wer sich besser mit Datenanalyse und Statistik auskennt, dürfte meine einfachen Abschätzungen hier für simpel (oder sogar: zu simpel) halten und sofort Ideen dafür haben, wie man es besser machen kann. Aber um jene Ideen zu verstehen, benötigt man in der Regel wieder spezielleres Vorwissen. Mir ging es, wie gesagt, um eine Untersuchung, die möglichst wenig an Vorwissen voraussetzt und für möglichst viele Leser im Detail nachvollziehbar ist. Aus dem gleichen Grunde habe ich auch meine Auswertungs- und Plotskripte hier vollständig online gestellt. (Letzteres noch aus einem anderen Grund: Ich selbst habe meine Programme zwar mehr als einmal durchgeschaut, aber manche Programmierfehler fallen erst auf, wenn mal jemand anders in den Quellcode schaut. Bei einer wissenschaftlichen Veröffentlichung spielen die Koautoren diese wichtige Rolle, bei einem Blogbeitrag fehlt diese Instanz.)
Bereits minimales Googeln zeigt, dass das, was ich hier argumentiere, alles andere als originell ist – was mich kein bisschen überrascht, gerade weil diese Argumentation auf der Hand liegt. Richard Muller hat sich (durchaus mit der Kritik kombiniert, die Klimaforscher würden die Rolle der natürlichen Variabilität unterschätzen) in der New York Times entsprechend geäußert und zeigt in seiner Ergänzung (PDF) auch ähnliche Kurven wie ich hier. Skeptical Science liefert die gleichen Argumente – und noch eine Reihe solcher, die weiter in die Tiefe gehen, als ich es hier leisten kann; als Teil ihres FAQ auch noch einmal hier.
Was da in der Berichterstattung schiefgeht, ist mir schleierhaft – dass solche missverständlichen Informationen wie über den angeblichen 15-Jahres-Stillstand weite Verbreitung bekommen, finde ich durchaus bedenklich. Das, was ich über Entwicklungen im Bereich Datenjournalismus lese (z.B. hier, hier) finde ich durchaus interessant, aber das ist wahrscheinlich sogar ein zu großes Wort für die einfachen Auswertungen, um die es in diesem Falle geht.
Für mich ist dieser weitere Ausflug in die Klimaforschung jetzt erst einmal wieder zuende. Einstein verstehen Teil IV steht schon in den Startlöchern. Aber ein paar interessante Themen für zukünftige Ausflüge bieten sich bereits jetzt an: Die wichtige Rolle der Ozeane wie hier argumentiert, die physikalisch grundlegende Frage nach der Energiebilanz, die Frage, ob man rein phänomenologisch – also ohne in die physikalischen Hintergründe einzusteigen – die kürzerfristigen Schwankungen beschreiben und zumindest zum Teil herausrechnen kann wie in Foster & Rahmstorf 2011 – und, als größeres Projekt, ein tieferes Eintauchen in die Berkeley Earth-Daten.
Zu den Kommentaren: Ich werde, wie bei ähnlichen Gelegenheiten, versuchen, so zu moderieren, dass die Diskussion direkt beim Thema dieses Beitrags bleibt (vgl. die Kommentarregeln hier). Durch die neue Antwort-Funktion werde ich aber wahrscheinlich nicht mehr darauf zurückgreifen müssen, meine Antwort grün abgesetzt dem entsprechenden Kommentar direkt hinzuzufügen.


Zitat aus dem neuesten IPCC-Report zu dem Thema:
“Despite the robust multi-decadal timescale warming, there exists substantial multi-annual variability in the
rate of warming with several periods exhibiting almost no linear trend including the warming hiatus since
1998.”
…
“Despite the robust multidecadal
timescale warming, there exists substantial multi-annual variability in the rate of warming with
several periods exhibiting almost no linear trend (including the warming hiatus since 1998).”
usw…
Ich gebe als Ergänzung mal Links und Quellen an: Diese bzw. ähnliche Zitate finden sich z.B. in “Climate Change 2013: The Physical Science Basis”, herunterladbar über diese Seite, in der Datei “Full Report” (PDF) ist z.B. der Abschnitt TS.4.2 ab S. 28 interessant. Leider sind da die Abbildungen nicht dabei – weiss jemand, warum das so ist und wo man die findet?
Leider wird da nicht klar gesagt, was genau mit dem “hiatus” (am Anfang steht er auch dort mal in Anführungszeichen) gemeint ist. Im weitergehenden Text hört es sich so an, als würde da an eine Untermenge von Jahren linear gefittet, aber das ist natürlich seinerseits kein unproblematisches Vorgehen.
Schoene Darstellung. Es ist, glaube ich, allgemein ackzeptiert, dass aus den Daten der globalen Temperatur alleine sich nichts besonderes zu den letzten 15 Jahren sagen laesst. Nichts spricht aus diesen Daten alleine dagegen, dass die Erwaermung so weitergeht.
Das ist aber nicht das wesentliche Problem. Das sieht man erst aus dem Vergleich mit den Resultaten der Klimamodelle. Wie wahrscheinlich ist es, dass eine Phase von x Jahren ohne positiven Trend vorkommt? Und zwar (im Gegensatz zu den hier auch erwaehnten Phasen um 1980 und 1990 herum) OHNE einen groeszeren Vulkanausbruch [El Chichon und Pinatubo] rein aus der internen Variabilitaet des Klimas. Die Antwort lautet, dass dies (bei 15 Jahre annaehernd flachen Trends) mittlerweile sehr unwahrscheinlich ist, oder -mit anderen Worten – dass die Modelle entweder die interne Variabilitaet unterschaetzen (1) oder den Erwaermungstrend ueberschaetzen (2). Beide Moeglichkeiten haben natuerlich einige Konsequenzen. Es aendert nicht die gesamte Klimaforschung, aber es ist auch nicht voellig vernachlaessigbar.
Was heißt in diesem Falle “ohne positiven Trend” bzw. “annähernd flach[e] Trends”? Bei der Mittelung sieht man das, siehe meine Abbildungen, ja gerade nicht.
Geht’s darum, an Unterzeiträume Geraden anzupassen?
Die anderen Punkte kann ich nachvollziehen. Die Resultate der Klimamodelle habe ich bei mir natürlich außen vor gelassen, und Vulkanausbrüche (oder eben nicht) sind bei meiner (rein heuristischen) Herangehensweise auch nicht berücksichtigt.
So ist es wohl.
MFG
Dr. W (der erneut sieht beim Zitierten jahrelang klimatologistisch angemessen konsumiert zu haben)
Die Berechtigung von Begriffen wie Erwärmungspause kann man aus einer statistischen Perspektive in Frage stellen, doch es ist falsch für die Erfindung dieser Begriffe die Medien – z.B. den Spiegel – verantwortlich zu machen.
Solche oder ähnliche Begriffe findet man durchaus in den Berichten führender Klimaforscher. Ich möchte aus Global Temperature Update Through 2012 von Hansen, Sato und Ruedi zitieren:
Weiter unten liest man zum Erwärmungsstillstand 1940-1975
Dass Begriffe wie “Erwärmungshiatus”, “Sitllstand der globalen Temperaturen” und ähnliche auch von Klimaforschern benutzt werden lässt sich einfach erklären: Klimaforschung ist eben mehr als das Wiedergeben von statistischen Trends. Klimaforschung will die Ursachen von Veränderungen und Entwicklungen bei Oberflächentemperatur und anderen Erdsystem-Messdaten erklären. Hansen, Sato und Ruedi erlären also den momentanen Erwärmungshiatus mit einer Kombination von natürlicher Variabilität und einer Abschwächung des Wachtums der erwärmungsantreibenden Kräfte (climate forcing).
Eine rein statistische Betrachtungsweise ist sowieso schwierig, weil wir immer versuchen, Gründe für Entwicklungen zu sehen. So liest man oben die scheinbar neutrale Beschreibung:
Doch die gleiche Kurve könnte man auch so beschreiben:
Eine fast geradlinige Erwärmung von 1910 bis 1940, eine Temperaturstagnation von 1940 bis 1975 und anschliessend eine Fortsetzung der Erwärmung wie sie schon 1910 bis 1940 zu beobachten war.
Wer vor allem die Erwärmung ab den 1970er Jahren betont, der hat offensichtlich die Treibhausgase im Visier, denn deren Anstieg könnte die Erwärmung ab den 1970er Jahren gut erklären. Die Erwärmung zwischen 1910 und 1940 dagegen ist mit einem weniger starken Anstieg von Treibhausgasen verbunden, obwohl die Erwärmung in diesem Zeitraum vergleichbar ist mit der Erwärmung ab den späten 1970er Jahren.
Man sieht: Der Mensch gibt sich nie mit Statistik allein zufrieden. Man fragt sich automatisch: Statistik von was? Was steckt dahinter? Und diese Fragen infizieren dann auch die statistische Betrachtung.
Direkt zu Hansen, Sato, Ruedi: Die beiden zitierten Aussagen kann man ja auch in meinen Bildern da oben nachvollziehen. Im fünf-Jahres-Mittel eine flache Kurve (die aber eben noch deutlich sichtbare Spuren der kurzfristigeren Fluktuationen enthält).
Die Stagnation ca. 1940 bis 1975 sieht man ja (bis hin zum gleitenden 25-Jahres-Mittel) bei mir auch.
Aber, wie gesagt, das ist ja beides in meiner (zugegebenermaßen vereinfachten) Auswertung auch sichtbar.
Der springende Punkt sind die Aussagen, die ich auf langfristige Mittelwert-Trends bezogen dort eben nicht finde, nämlich eben den behaupteten Stillstand in den letzten 15 Jahren. Was steckt hinter solchen Aussagen?
Schöne Darstellung, die übrigens auch voll mit den Aussagen des neuen IPCC-Berichts übereinstimmt. Der schreibt in der Summary for Policy Makers (Seite 3, online unter http://www.ipcc.ch):
“Due to natural variability, trends based on short records are very sensitive to the beginning and end dates and do not in general reflect long-term climate trends. As one example, the rate of warming over the past 15 years (1998–2012; 0.05 [–0.05 to +0.15] °C per decade), which begins with a strong El Niño, is smaller than the rate calculated since 1951 (1951–2012; 0.12 [0.08 to 0.14] °C per decade).”
(Man beachte dabei besonders die angegebenen Unsicherheitsintervalle.)
Wer selbst mit den Daten spielen möchte, kann dies am leichtesten mit der netten Smartphone-App CliMate tun. Die hat eine Funktion Climate Analyser, die die Daten so wie im Beitrag oben als gleitende Mittelwerte darstellt, wobei man den Mittelungszeitraum mit einem Schieberegler durchfahren kann – was oben als viele Einzelgrafiken dargestellt ist kann man da also mit einem Swipe mit dem Zeigefinger ansehen.
(test. Kann nicht mehr kommentieren)
Scheint zu funktionieren. Ich schaue mal, ob der Spamfilter irgendwo angeschlagen hat, wo er nicht sollte…
Im Spamfilter ist nichts hängengeblieben. Irgendein Problem beim Absenden des Kommentars?
Korrektur: Jetzt habe ich die Kommentare im Spamfilter gefunden. Allerdings nur die Testkommentare, keinen, der soweit ich sehen kann zum freischalten gedacht war.
Wie müßte denn eine Temperaturentwicklung aussehen, bei der beim Mitteln über 9 oder 11 Jahren noch eine deutliche Stagnation sichtbar wäre?
Dafür geben die oben gezeigten Kurven direkt ein Beispiel: Die dort gezeigte Entwicklung zwischen etwa 1940 und 1970. Da ist selbst dann, wenn man sich nur auf den ersten Abschnitt (sagen wir mal: 1940 bis 1955) beschränkt, in der 11-Jahres-Mittelungskurve eine Art Plateau zu sehen.
@Poessel
“Was heißt in diesem Falle “ohne positiven Trend” bzw. “annähernd flach[e] Trends”? Bei der Mittelung sieht man das, siehe meine Abbildungen, ja gerade nicht.
Geht’s darum, an Unterzeiträume Geraden anzupassen?”
Genau. Es kann schon gut sein, dass meinethalben LOWESS oder irgendeine andere Funktion in mancher Hinsicht elegantere oder robustere Eigenschaften hat, ein linearer Trend ist aber auch nicht per se schlecht. Die etwa dekadische Trends wurden viel in der Oeffentlichkeit kommuniziert und es scheint mir im Prinzip legitim mal nachzuschauen, wie die Trends so im Vergleich zu den Modellen ausschauen.
In dem Zusammenhang vielleicht auch
http://scienceblogs.de/primaklima/2012/04/21/trends-trends-trenbs-der-neue-hadcru4-datensatz-ist-da-und-die-erde-erwarmt-sich-immer-noch/
insbesondere Abbildung 4 und 5.
OK, das ist eine schöne Darstellungsweise, insbesondere die erwähnten Abbildungen 4 und 5. Allerdings habe ich dafür, wie man diese letzten beiden Abbildungen liest, auch nach den dort gebotenen Erklärungen, noch keinen rechten Blick entwickelt.
@Markus Pössel:
danke!
Stefan Rahmstorf berichtet gerade in der KlimaLounge von einem Artikel, der argumentiert, dass Temperaturkurven wie jene, die ich hier angeschaut haben, die Erwärmung unterschätzen. Die Autoren, Cowtan und Way, haben ein soweit ich sehen kann recht cleveres neues Verfahren entwickelt, Temperaturabschätzungen für diejenigen Bereiche der Erdoberfläche vorzunehmen, von denen keine direkten Messdaten vor Ort, aber Satellitendaten vorliegen. Im Ergebnis liegt dann der Trend der letzten 15 Jahre ziemlich genau bei dem vom IPCC genannten Langzeittrend. Der Blogbeitrag ist hier: https://scilogs.spektrum.de/klimalounge/erwaermung-unterschaetzt/
Ihr Kommentatorenfreund war auch mal händisch an oder auf den GISS-Daten und hat wie folgt visualisiert:
-> http://s14.directupload.net/images/131114/6lsn8icq.jpg
Natürlich auch weitergehender und Trends für bestimmte Zeiträume feststellend.
Die zitierte Angabe ist korrekt, der Trend für die letzten 15 Jahre wie für den Zeitraum 1880/01-2013/08 ist ca. +0,06 C / Dekade.
Der Trend der letzten 12 Jahre ist minimal negativ.
MFG
Dr. W (der sich den Daten nur deshalb angenommen hat, weil der Durchschnitt der IPCC-Prognosen ca. +0,32 C / Dekade vorhersagt, die Datenlage über 133 Jahre und 9 Monate eine Erwärmungstendenz von ca. +0,065 C / Dekade belegt)
PS:
Hier mal der selten gezeigte Zeitraum 1880/01-2013/07 mit den monatlichen Werten auf der X-Achse aufgetragen.
-> http://s7.directupload.net/images/131114/98zw2q45.jpg (wieder GISS)
Wie wenig solche Sub-Trendlinien aussagen, ist ja nun aber in dem oben verlinkten Beitrag http://scienceblogs.de/primaklima/2012/04/21/trends-trends-trenbs-der-neue-hadcru4-datensatz-ist-da-und-die-erde-erwarmt-sich-immer-noch/ schön zu sehen.
Es ist insgesamt seit 1880 ca. 0,9 C wärmer geworden, ein Großteil der Erwärmung entstand zwischen ca. 1972 und ca. 1998: nämlich +0,5 C
Die Stagnation seit 1998 ist insofern schon interessant, weil der atmosphärische CO2-Anteil schneller steigt als zuvor.
Die Trends und Sub-Trends (Ihr Begriff) sind natürlich nicht so-o aussagekräftig, loge!
Was allgemein auffällt ist aber die Betonung eines Trends, wenn er konveniert, und die korrekte relativierende Einordung, wenn er es nicht tut.
Hier ist also eine Falle (in die auch oft hineingetapst wird) aufgestellt.
MFG
Dr. W
“Was allgemein auffällt ist aber die Betonung eines Trends, wenn er konveniert, und die korrekte relativierende Einordung, wenn er es nicht tut.”
Genau!
Was den Großteil selbsternannter Klimawandel- “Skeptiker” betrifft, steht ja fest, dass ein langfristiger Erwärmungstrend jedesmal wiederlegt ist, sobald es eine temporäre Fluktuation in die andere Richtung gibt. Eines der Probleme dürften ungewohnte Zeitskalen sein. Was sich innerhalb einer menschlichen Lebensspanne (trotz Journalistisch ausgeschmückter Sensationsmeldungen) unmerklich langsam abspielt ist in (geo-) historischen Maßtäben gemessen ein offensichtlich rasend schneller, beispielloser Wandel, der sich spätestens für kommende Generationen als fatal erweisen kann.
@Dr.Webbaer
Ein solcher Graph zeigt eben gerade, dass eine rein statistische Betrachtungsweise nicht viel bringt ausser man geht von der Nullhypothese aus, also der Hypothese, es gebe keine Kräfte, die das Klima verändern.
Die Klimaforschung startete aber schon mit der Annahme, es gebe “Forcings”, die das Klima verändern und die Klimaforschung kenne diese oder komme ihnen immer näher. So wurde der Stand-Still der Temperaturen 1940 bis 1975 mit den dannzumal stark ansteigenden Russpartikeln und anderen Aerosolen erklärt. Aber schon dazumal – also während dem Stand-Still – wurde von vielen Kliamtologen/Physikern ansteigende Temperaturen in naher Zukunft aufgrund der steigenden Treibhausgase vorausgesagt.
Unter der Annahme, dass die von Jahr zu Jahr steigenden Treibhausgase das Strahlungsungleichgewicht immer weiter erhöhen kann man aber auch einiges voraussagen. Insbesondere darf dann die “Temperaturpause”, die wir heute meinen zu erleben, nicht mehr 10 oder 20 Jahre weiter anhalten.
Die Datenlage zeigt, dass ein Großteil der Erwärmung theoretischer Art ist, dass Prognosis und Datenlage auseinander laufen, zurzeit ca. um den Faktor 5,5.
MFG
Dr. W
“dass Prognosis und Datenlage auseinander laufen, zurzeit ca. um den Faktor 5,5.”
Das ist natürlich Blödsinn.
Ralph, die Anmerkung bezog sich auf die durchschnittliche Erwärmungs-Prognose von ca. +3,2 C / Dekade bis 2100, die sich aus den Szenarien und Modellrechnungen ableiten lässt, und dem aus der Datenlage abgeleiteten Gesamt-Erwärmungs-Trend (“Lineare Progression”) von ca. +0,06 C / Dekade.
Man könnte hier den wie oben beschrieben festgestellten Trend und den theoretischen, prognostischen Trend wie berechnet in Relation setzen wollen…
MFG
Dr. W (der immer auch notiert, wenn Skeptiker in Anführungsstrichen geschrieben werden)
Korrektur:
* Lineare Regression
MFG
Dr. W (der nichts gegen eine Vorschau hätte)
Leider verfehlt der Artikel nach meinem Dafürhalten das eigentliche Thema. Dies kann wohl kaum sein, dass gleitende Durchschnitte oder Standardabweichungsverfahren mit größere kurzfristige Schwankungen konsequent ausbügeln. Mit zunehmeder Länge Zeitfensters dann eben auch größere. Dieser Umstand ist sowohl trivial, als auch schon im Wort “Durchschnitt” enthalten. Auch die bei gleitenden Durchschnitten regelmäßig folgende Diskussion um die korrekte Wahl des Zeitfensters dürfte irrelevant, da fruchtlos sein.
Entscheidend ist, dass gleitende Durchschnitte per se keine Zukunftsprognise erlauben. Einmal angenommen, die Klimaaktivitäten würden sich ändern. Dann würde ein gleitender Durchschnitt dies erst nach entsprechend langer Zeit registrieren, während die Durchschnittsfans trendfolgend an die Daten der Vergangenheit glauben. Tatsächlich ist aufgrund des Berechnungsverfahrens jede Verlängerung von auf historischen Daten basierten Durchschnittskurven in die Zukunft mathematisch schlicht falsch. Wissenschaftlich ist das bei so komplexen Phänomenen wie dem Klima im besten Fall spekulativ. Möglicherweise müsste man es sogar als unseriös bezeichnen.
Falls man angesichsts dieser mißlichen Lage nicht nur mit Verdrängungen einfacher Voraussetzungen oder wilden Behauptungen agieren und weitere Erkenntnisse gewinnen wollte, wäre die Hinzufügung externer Datenpunkte, also die Anwendung von Korrelationsverfahren vielleicht eine Hilfe. An der Stelle würde mich einmal interessieren, inwieweit Temperaturzuwächse einerseits, sowie Kohlendioxidproduktion überhaupt korrelieren. Wie ein Teilnehmer oben angedeutet hat, scheint eben diese Korrelation schwächer zu werden: Der Ausstoß an Kohlendioxid steigt, gleichzeitig nimmt die Erwärmungsdynamik zumindest nicht zu.