Einstein verstehen VIII: Bezugssystemwechsel und freie Teilchen
BLOG: RELATIV EINFACH

Zwei hintereinander ausgeführte affine Transformationen ergeben eine affine Transformation
Dass sich zwei hintereinander ausgeführte affine Transformationen, nämlich eine affine Transformation A, die uns vom Bezugssystem S zum Bezugssystem S’ bringt und eine affine Transformation B, die uns von S’ nach S” bringt, auch als eine einzige affine Transformation C schreiben lassen, die uns direkt vom Bezugssystem S zum Bezugssystem S” bringt, lässt sich, wie im Haupttext bereits gesagt, direkt ausrechnen. Hier:
Die Transformation A vom System S (Koordinaten: x, y, z, t) zum System S’ (Koordinaten: x’, y’, z’, t’) ist unserer Definition nach affin, wenn sie sich (wie überall hier die in Teil VI eingeführte Kurzschreibweise nutzend) schreiben lässt als:
wobei die axx, axy, … jeweils Konstanten sind (also nicht von x, y, z oder t abhängen).
Ganz analog ist die Transformation B vom System S’ zum System S” (Koordinaten: x”, y”, z”, t”) affin, wenn sie sich schreiben lässt als
mit wiederum konstanten bxx, bxy, bxz, … und so weiter.
Um auszurechnen, wie die Transformation von S nach S” aussieht, wie sich also die Werte x’, y’, z’, t’ für ein gegebenes Ereignis direkt aus den Werten x, y, z, t für dasselbe Ereignis ergeben, müssen wir in den gerade genannten Gleichungen für die x”, y”, z”, t” überall auf der rechten Seite die Koordinaten x’, y’, z’ und t’ durch die x, y, z, t ausdrücken. Welche Gleichungen wir dafür einsetzen müssen, sagen uns die oben angegebenen Formeln zur Transformation A, in denen ja gerade ausgedrückt ist, welche Werte x’, y’, z’, t’ sich aus gegebenen Werten für x, y, z, t ergeben.
Das Ergebnis, hier gleich zusammengefasst geschrieben, ist
wobei die Konstanten cxx, cxy, cxz etc. gegeben sind durch
Das sind zwar eine Menge nicht allzu kurzer Formeln, die sich aber mit etwas Geduld direkt berechnen lassen, ohne dass man dabei über die Grundrechenarten Addition und Multiplikation hinausgehen müsste. (Für diejenigen, die lineare Algebra kennen, sind das schlicht die Regeln der Matrix-Multiplikation.)
Insbesondere hat dies dieselbe Form wie für die Transformationen A und B; in jeder Formel kommen x, y, z, t jeweils in der ersten Potenz und mit konstanten Koeffizienten cxx, cxy, cxz etc. vor, zusätzlich zu konstanten Summanden cxc, cyc, czc, ctc. Demnach handelt es sich, wie behauptet, auch beim direkten Übergang von S zu S” um eine affine Transformation.


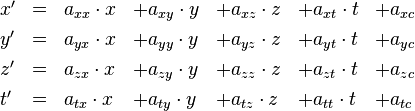
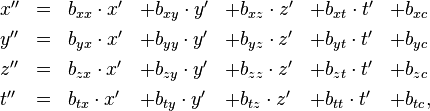
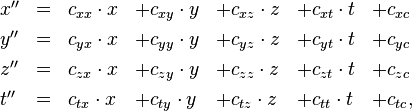
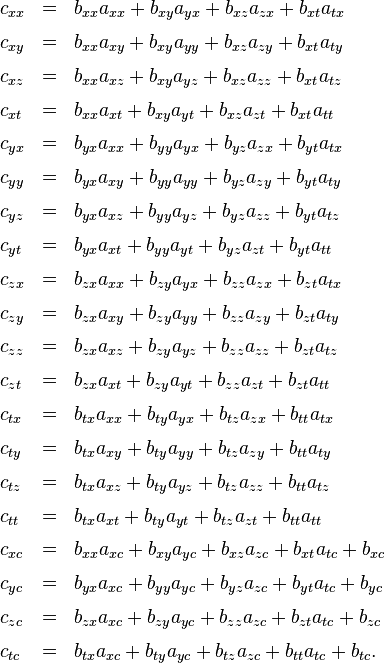
1) Da sind offenbar einige Hyperlinks verunglückt; etwas von der Form “http://http://http://http://http://https://scilogs.spektrum.de/relativ-einfach/einstein-verstehen-vii-bezugssystemwechsel-in-der-klassischen-mechanik/” kann nicht funktionieren.
2) »Wir wenden uns stattdessen im nächsten Teil denjenigen Koordinatentransformationen der klassischen Physik aus Teil VII zu, die gerade nicht affin sind: beschleunigten Verschiebungen des Raumnullpunktes und zeitabhängigen Drehungen der Koordinatenachsen, wiederum mit der Frage: Was bedeuten die entsprechenden Bezugssystemwechsel für die Bahnen freier Teilchen?«
Mit welcher didaktischen Motivation? Solche Transformationen genügen nicht dem speziellen Relativitätsprinzip und gehören nicht zur SR. In seinem populären Büchlein von 1916 hat Einstein aus guten Gründen dergleichen schliesslich auch nicht bei der SR abgehandelt.
Hyperlinks: Da spinnt das Content Management System der Scilogs gerade herum, sorry. Die zuständigen Kollegen suchen gerade nach dem Fehler; ist hoffentlich bald wieder OK.
Beschleunigungen: So etwas braucht man, um Trägheitskräfte einzuführen. Die wiederum sind sinnvoll, um Inertialsysteme zu definieren (alternativ von “kräftefreien Teilchen” zu reden ist nicht ganz urnproblematisch, siehe den Übergang zur ART). Mir ist aber bewusst, dass die Grundlage , die ich gerade entwickle, vergleichsweise tief gehen. Wie kurz angedeutet: In der Endversion von “Einstein verstehen” habe ich stattdessen vor, eine Zusammenfassung der bisherigen Vorbereitungsteile an den Anfang zu stellen. Nur wer es genauer wissen möchte, wem das Vorwissen fehlt oder wer bzw. entsprechende Missverständnisse aufklären muss, dürfte dann noch eine Ebene tiefer gehen.
…so, jetzt sollten alle Hyperlinks wieder richtig sein!
MP: “Anders formuliert heißt das: Gilt in einem bestimmten Bezugssystem die Newton’sche Aufteilung, nach der sich eine bestimmte Klasse von Teilchen (“freie Teilchen” bzw. “kräftefreie Teilchen”) mit konstanter Geschwindigkeit entlang von Geraden bewegt, während Teilchen, die nicht zu dieser Klasse gehören durch auf sie wirkende Kräfte von solchen freien Bahnen abgelenkt werden, dann gilt genau dieselbe Unterteilung in kräftefreie und kraft-beeinflusste Teilchen auch in jedem Bezugssystem, welches mit dem erstgenannten Bezugssystem durch eine bahnerhaltende affine Koordinatentransformation zusammenhängt. Ein Teilchen, das im ersten Bezugssystem einer freien Bahn folgt, tut dies auch im zweiten System, und umgekehrt.”
Gilt das auch für Photonen?
Bislang ist hier von Photonen noch nicht die Rede, und um quantenmechanische Komplikationen wird es in dieser Einführung auch nicht gehen, aber prinzipiell: Ja, wenn Lichtteilchen in einem der Bezugssysteme mit konstanter Geschwindigkeit Geradenbahnen folgen, gilt das dem hier dargelegten nach auch in anderen Bezugssystemen, die man über affine Transformationen erreicht.
Hallo Dr. Pössel,
eigentlich könnte Teil IX kommen.
mit freundlichem Gruß
Markus Pössel schrieb (16. Januar 2016):
> Tatsächlich gilt: Eine Koordinatentransformation, die jede mit konstanter Geschwindigkeit durchlaufende Geradenbahn in eine mit konstanter Geschwindigkeit durchlaufende Geradenbahn überführt und dabei, das muss man zusätzlich annehmen, keine Punkte “ins Unendliche verschiebt” (Raum- und Zeitpunkte mit endlichen Koordinatenwerten haben auch im zweiten Bezugssystem endliche Koordinatenwerte), ist zwangsläufig eine affine Koordinatentransformation.
Stattdessen gilt: Eine Koordinatentransformation, die jede mit konstanter Koordinaten-Geschwindigkeit durchlaufende Koordinaten-gerade Bahn in eine mit konstanter Koordinaten-Geschwindigkeit durchlaufende Koordinaten-gerade Bahn überführt und dabei keine Punkte “ins Unendliche verschiebt”, ist zwangsläufig eine affine Koordinatentransformation.
Die Begriffe “Geschwindigkeit (eines bestimmten Beteiligten bzgl. Mitgliedern eines Inertialsystems)” und “Bahnform (einer geeigneten Teilmenge von Mitgliedern eines Inertialsystems)” sind dagegen Koordinaten-frei definiert und feststellbar. Sie bestehen unveränderlich für jegliche Eins-zu-Eins-Zuordnung von Koordinaten-Tupeln.
Die Transformations-Beziehungen zwischen irgendwelchen zwei Eins-zu-Eins-Zuordnung von Koordinaten-Tupeln sind allerdings wesentlich allgemeiner als (nur) affine Koordinatentransformationen.
p.s.
SciLogs-Kommentar-\(\LaTeX\)-Test:
“\( s^2 : \mathcal E \times \mathcal E \rightarrow \mathbb R. \)” wird dargestellt als “\( s^2 : \mathcal E \times \mathcal E \rightarrow \mathbb R.\)”
@Frank Wappler: In den vorangehenden Teilen ist die Geschwindigkeit ja über (physikalisch sinnvolle, also nicht beliebige) Koordinaten definiert worden. Insofern: Was ich da schrieb ist so, wie ich die Begriffe eingeführt habe, richtig.
Ihr (wiederholtes) Vorgehen, Ihren eigenen Sprachgebrauch zum einzig Wahren zu erklären und alles, was davon abweicht (wie in diesem Falle) für “falsch” zu erklären, ist irreführend und letztlich auch schlampig, da es wichtige Informationen zum Kontext (wie sind die Begriffe in dieser Artikelserie definiert) unter den Tisch fallen lässt. Warum dieser Mangel an Flexibilität? Sie müssen doch selbst merken, dass das die Kommunikation noch weiter erschwert.
Markus Pössel schrieb (3. Juli 2018 @ 22:59):
> In den vorangehenden Teilen ist die Geschwindigkeit ja über […] Koordinaten definiert worden.
Das derart Definierte ist folglich als Koordinaten-Geschwindigkeit zu bezeichnen.
> (physikalisch sinnvolle, also nicht beliebige) Koordinaten
Wird es nach Jahren des Hinhaltens denn nicht endlich mal zu einer nachvollziehbaren Definition kommen, welche Koordinaten-Zuordnungen “physikalisch sinnvollen Koordinaten” genannt werden sollen ??
Dass jeweils “Eindeutigkeit” (“jedem möglichen Punktereignis eindeutige Koordinatenwerte“) bzw. Invertierbarkeit der Zuordnung gefordert ist, dürfte ja selbstverständlich und unkontrovers sein.
Aber was darüberhinaus noch ?!?
Meine naive Vermutung in Anlehnung an die vorliegenden Teile der Online-Einführung wäre ja, dass eine Koordinaten-Zuordnung \[ \frac c : \mathcal E \times \mathcal E \rightarrow \mathbb R^n \] genau dann “physikalisch sinnvoll” genannt werden soll,
falls sich eine Funktion \[ f_{\frac c} : \mathbb R^n \times \mathbb R^n \rightarrow \mathbb R \] angeben ließe,
so dass für je zwei Elemente \(A\) und \(B in \mathcal E\) gilt:
\[ f_{\frac c}[ \, \frac c[ \, A \, ] \, \frac c[ \, B \, ] \, ] \mapsto d[ \, A, \, B ] \],
wobei \[ d : \mathcal E \times \mathcal E \rightarrow \mathbb R \] ein bestimmtes, nachvollziehbares, physikalisch sinnvolles, vorab Koordinatenfrei definiertes Abstandsmaß bezeichnet.
Allerdings träfe das ganz ausdrücklich auf jede beliebige invertierbare Koordinaten-Zuordnung \(\frac c \) und jedes Abstandsmaß \(d\) zu, denn die entsprechende Funktion \( f_{\frac c} \) ließe sich ja unmittelbar durch
\[ f_{\frac c}[ \, a, \, b \, ] \mapsto d[ \frac c^{-1}[ \, a \, ], \frac c^{-1}[ \, b \, ] \, ] \]
angeben.
p.s.
Mit der mir eigenen Schlampigkeit und Unflexibilität verlasse ich mich zunächst darauf, dass \(\LaTeX\)-Formatierung von Kommentaren baldigst auch auf dieser SciLogs-Seite unterstützt wird …
@Frank Wappler: Nö, es ist völlig legitim, das Ergebnis nur “Geschwindigkeit” zu nennen. Genau dieser inflexible Ansatz, den Sie da in punkto Begriffe verfolgen, macht die Kommunikation so schwierig und eine Reihe Ihrer Äußerungen so irreführend. Sprache ist flexibel. Und für die meisten hier Mitlesenden schränkt steife Anwendung von Fachbegriffen die Verständlichkeit ein, während jeder Rückgriff auf Alltagsbegriffe hilft.
Zu “Jahren des Hinhaltens” – Ihre Anspruchshaltung ist schon ziemlich dreist. Wie schon mehrfach geschrieben: Dieses Blog läuft für mich “nebenbei”. Ich schreibe Beiträge, wenn ich neben meinen anderen Tätigkeiten Zeit dafür finde, und dann als Mischung dessen, was gerade aktuell ist, was mich gerade selbst beschäftigt, was an Grundlagen ich interessant finde etc.
Dass Sie hier (jetzt ja schon wiederholt!) mit einem Ton ankommen, als hätten Sie etwas bei mir mit bindendem Vertrag bestellt, bezahlt, und ich hätte dann nicht geliefert, ist einfach komplett daneben. Und hebt meine Motivation ganz sicherlich nicht, was einen Blogbeitrag über Koordinaten angeht.
Markus Pössel schrieb (4. Juli 2018 @ 11:46):
> Wie schon mehrfach geschrieben: Dieses Blog läuft für mich “nebenbei”. Ich schreibe Beiträge, wenn ich neben meinen anderen Tätigkeiten
Da dieser SciLog offenbar die einzige Form Barriere-freier Beziehung des MPIA mit der Offentlichkeit darstellt, definiert sich dadurch, wie engagiert und verantwortungsvoll das MPIA Barriere-freie Beziehungen mit der Offentlichkeit pflegt.
> was einen Blogbeitrag über Koordinaten angeht.
Einen SciLogs-Beitrag über Koordinaten kann man sich meinetwegen gern sparen; schließlich geht es dabei lediglich um (sprichwörtlich) “x-bliebige” eins-zu-eins-(invertierbare)-Zuordnungen” von Ereignissen bzw. Beteiligten und deren individuellen Anzeigen zu reell-wertigen n-Tupeln.
Der 24. September 2016 @ 10:56 in Aussicht gestellte “gesonderte [SciL]ogbeitrag zur Frage von Koordinaten und koordinatenfreien Darstellungen“ ist (für mich) vielmehr hinsichtlich der dabei angedeutenten “koordinatenfreien Darstellungen” von Interesse (die nachträglich in die Menge reell-wertiger n-Tupel und durch deren “natürliche” topologische bzw. metrische Eigenschaften abgebildet werden mögen).
p.s.
SciLogs-Kommentar-HTML-Test:
“𝔠<sup>-1</sup>” wird dargestellt als: “𝔠;-1″.
@Frank Wappler: Hoppla, da jagt ja eine falsche Aussage die nächste…
Dieses SciLog ist kein Angebot des MPIA, sondern ein Blog, das ich als einzelner Wissenschaftler, wenn natürlich auch mit engem Bezug zu meiner Arbeit am Haus der Astronomie bzw. am MPIA, schreibe. Die MPIA-Öffentlichkeitsarbeit sieht vom Tag der Offenen Tür und öffentlichen Vorträgen an diversen Orten über Pressemitteilungen und die direkte Beantwortung von Anfragen ganz anders aus.
Bei den Koordinaten sieht es mir nach dem, was Sie schreiben, doch noch aus, als wäre auch für Sie ein entsprechender Beitrag wichtig. Physiker verknüpfen ihre Koordinaten ja ganz absichtlich mit physikalischen Größen, so dass das Ergebnis keine beliebige Zuordnung hat, sondern möglichst dicht an der Physik ist. Daher sind hier beim Thema Gleichzeitigkeit ja auch die Ausführungen zur in den üblichen Standardkoordinaten dargestellten Lorentz-Transformationen hilfreich. Gerade weil es nicht um willkürliche Zahlenwerte geht sondern um physikalische Bezüge.
P.S.: Ich weiß gar nicht, ob man die SciLogs tatsächlich als barrierefrei einstufen kann; wer z.B. nur eingeschränkt sehen kann, bräuchte ja trotzdem zusätzliche Hilfsmittel, um an die Inhalte zu kommen.
Markus Pössel schrieb (5. Juli 2018 @ 12:48):
> Dieses SciLog ist kein Angebot des MPIA
Das ist nicht zu bestreiten.
In Ermanglung eines SciLogs (oder eines vergleichbar öffentlichem, archivierten und Barriere-freien Mediums), das vom MPIA ausdrücklich angeboten würde, bleibt dieses SciLog allerdings (meiner bisherigen Kenntnis nach) das dahingehend auffindbarste.
> Die MPIA-Öffentlichkeitsarbeit […] die direkte Beantwortung von Anfragen
Bietet das MPIA etwa an, Anfragen öffentlich und archiviert (d.h. mit URL versehen, wie wir es von den SciLogs her kennen und ggf. nutzen) zu stellen ??
> Physiker verknüpfen ihre Koordinaten ja ganz absichtlich mit physikalischen Größen […]
Von der in Aussicht stehenden Darstellung und Diskussion, wer welche Absichten durch das eine oder andere Anknüpfen von Koordinaten verfolgt und ggf. verwirklicht werden mögen, verspreche ich mir jedenfalls, dass die Rolle der physikalischen Größen bzw. ihrer jeweiligen Werte dadurch gewürdigt und betont wird, und dass sich alles Anschließende darauf konzentrieren kann.
> P.S.: Ich weiß gar nicht, ob man die SciLogs tatsächlich als barrierefrei einstufen kann; wer z.B. nur eingeschränkt sehen kann, bräuchte ja trotzdem zusätzliche Hilfsmittel, um an die Inhalte zu kommen.
Wer bestimmte Hilfs
modellemittel benennen kann, hat allein dadurch schon eine Barriere weniger …@Fred Wappler: Das ist eine so krude Mischung aus Unlogik, Ablenkung und dem Kapern eines bereits definierten Begriffs (Barrierefreiheit) dass ich mir eine längere Antwort erspare. Auf diese Weise kann man nicht vernünftig diskutieren.