Dies ist die Hintergrundseite zum Blogeintrag Einstein verstehen Teil III: Gleichzeitigkeit. Wie dort beschrieben, hat die Seite mehrere Funktionen: Sie versammelt ein par zusätzliche Textteile, in denen Aussagen aus dem Haupttext genauer erklärt werden, und sie zeigt die ursprüngliche Version des Blogeintrags – vor Einarbeitung etwaiger Änderungen, die sich aus den Kommentaren der Leser ergeben haben. Abweichend vom Vorgehen in den ersten beiden Teilen gilt diesmal aber: Kommentare zum Haupttext, die ich dort nicht veröffentlicht habe, da sie der Schritt-für-Schritt-Erklärung vorgreifen oder in anderer Weise unkonstruktiv oder unangemessen sind, finden sich nicht mehr auf der Hintergrundseite (die lief letztes Mal über!), sondern extern auf einer Unterseite meiner Webseiten am Albert-Einstein-Institut.

1. Vertiefungen zum Blogeintrag

Beispiele dafür, wie nicht synchronisierte Uhren zu falschen Messergebnissen für die Zeitdauer führen

Wie nicht synchronisierte Uhren zu falschen Ergebnissen führen, lässt sich am einfachsten an extremen Alltagsbeispielen verstehen. Die Effekte, um die es später bei der Speziellen Relativitätstheorie gehen wird, sind natürlich ungleich kleiner.

1. Flugreise mit Zeitzonen

Kurz vor dem Einsteigen habe ich noch auf die Flughafenuhr in Frankfurt geschaut: 10:42 Uhr konnte ich dort ablesen. Nach dem Aussteigen am New Yorker Flughafen John F. Kennedy der Blick auf die dort angebrachte Uhr: 14:20 Uhr. Hat mein transatlantischer Flug demnach 3 Stunden und 38 Minuten gedauert?

Natürlich nicht, weil die beiden Uhren, an denen ich mich orientiert habe, nicht synchron laufen, sondern eine konstante Anzeigedifferenz von 6 Stunden haben. Sie entspricht dem Unterschied der Zeitzonen “Mitteleuropäische Zeit” [MEZ] und “Sommerzeit der Ostküste Amerikas” [EST]. Tatsächlich hat meine Reise rund 9 Stunden und 38 Minuten gedauert.

2. Zeitumstellung

In den Daten eines Digitalfotos lese ich, dass ich dafür heute um 14:33 Uhr auf den Auflöser gedrückt habe. Auf meiner Armbanduhr lese ich 19:52 Uhr ab. Sind seit dem Foto demnach rund 5 Stunden und 19 Minuten vergangen?

Nein, denn wie sich herausstellt laufen die beiden Uhren auch nicht annähernd synchron. Meine Kamera zeigt nach wie vor Winterzeit an (und schreibt das auch so in die Fotodateien), während meine Armbanduhr derzeit auf Sommerzeit gestellt ist. Seit der Aufnahme sind daher nur rund 4 Stunden und 19 Minuten vergangen.

3. Uhren-Ungenauigkeit

Direkter Vergleich zeigt: Als meine Küchenuhr auf 19:57:00 Uhr stand, zeigte mein Wecker 19:58:27 an, und meine Armbanduhr zeigte 19:59:15.

Dementsprechend sind diese Uhren nicht synchronisiert; wenn ich auf der Küchenuhr ablese, wann ich das Haus verlasse und auf meiner Armbanduhr nachschaue, wann ich wiederkomme, werde ich die Dauer meiner Abwesenheit um 2 Minuten und 15 Sekunden überschätzen.

Fazit

In den ersten beiden Fällen lässt sich der die Synchronisation störende Umstand (Zeitzonen/Sommer- vs. Winterzeit) leicht beseitigen. Im letzten Falle kann man die Uhren zumindest im Rahmen der Ablesegenauigkeit vergleichsweise einfach auf die gleiche Zeit einstellen – auch wenn diese Übereinstimmung im Laufe der folgenden Tage wieder verloren gehen wird: für die 10+ Stunden, die ich tagsüber aus dem Haus bin, sollte es reichen.

Insofern sind die hier gezeigten Beispiele von anderer Art als die grundlegenden Synchronisationsprobleme, die uns im Laufe von Einstein verstehen noch begegnen werden. Dass eine aus den Anzeigen nicht hinreichend synchronisierter Uhren gebildete Zeitdifferenz problematisch ist, gilt allerdings hie wie dort – und mehr sollen diese Beispiele auch nicht zeigen. 

 

Symmetrie und Transitivität der Gleichzeitigkeitsdefinition durch Signalaustausch

Symmetrie der Gleichzeitigkeitsdefinition

Dass Uhr A mit Uhr B tatsächlich synchron läuft, wenn Uhr B mit Uhr A synchron läuft, lässt sich wie folgt zeigen.

Dass Uhr B mit Uhr A synchron läuft, bedeutet laut unserer Definition: Sei 2·Δt die Zeit, die ein Signal benötigt, um (mit Uhr A gemessen) entlang des von uns vorgegebenen Weges von A nach B und wieder zurück zu laufen. Dann kommt ein Signal, das zur Zeit t₀ (Anzeige der Uhr A) bei A losläuft, zur Zeit t₀ + Δt (Anzeige der Uhr B) bei B an.

Wenn nun aber 2·Δt die Zeit ist, die ein Signal benötigt, um (auf der Uhr A gemessen) von A nach B und zurück zu reisen, dann ist 2·Δt auch die Zeit, die ein Signal benötigt, um (auf der Uhr B gemessen) von B nach A und zurück zu reisen – bis auf kleinere Messfehler, die eine Rolle spielen mögen, wenn wir die Situation praktisch umsetzen, die uns beim gedanklichen Durchspielen aber nicht beschäftigen müssen. Die Gleichheit ergibt sich daraus, dass wir die Situation symmetrisch gestaltet haben und außerdem davon ausgehen, dass die Naturgesetze nicht von den Orten der Uhren A und B abhängt. 

Jetzt betrachten wir ein Signal 1, das zur Zeit t₁ von der Uhr B losläuft. Wann erreicht es die Uhr A?

Stellen wir uns vor, von der Uhr A sei vorher, zu einer Zeit, die wir t₀ nennen, ein Signal 2 zur Uhr B losgelaufen, das genau zu dem Zeitpunkt bei B eintreffen möge, bei dem das uns interessierende Signal 1 von B aus seine Reise zur Uhr A antritt. Das Signal 2 fliegt direkt nach seinem Eintreffen auf dem gleichen Wege zurück zum Ort A.

Signal 1 und Signal 2 machen sich demnach zum gleichen Zeitpunkt von B auf den Weg zu A; ihre Fortpflanzung findet entlang des gleichen Weges statt und wird von den gleichen physikalischen Gesetzen bestimmt; dementsprechend laufen Signal 1 und Signal 2 genau gleich von B nach A und kommen insbesondere auch gemeinsam zur gleichen Zeit am Ort A an.

Signal 2 hat für seine Rundreise den Voraussetzungen nach (siehe oben) die Zeit 2·Δt gebraucht. Die Zeit 2·Δt ist schließlich die Zeit, die solch ein Signal für die Rundreise von A nach B zurück nach A benötigt.

Signal 2 kommt demnach zur Zeit t₀ + 2·Δt wieder bei A an.

Dass Uhr B mit Uhr A synchron läuft, heisst gemäß unserer Definition, dass die Zeit t₁, zu der Signal 2 bei B eintrifft und die beiden Signale gemeinsam ihre Reise in Richtung A antreten, gerade t₀ + Δt ist.

Dass wiederum bedeutet aber, dass die Uhr A beim Eintreffen des Signals 1 die Zeit t₀ + 2·Δt = t₁ + Δt anzeigt. Das wiederum war aber, siehe oben, das Kriterien dafür, dass die Uhr A mit der Uhr B synchron läuft. Unser Gedankenexperiment hing nicht davon ab, welchen Zeitpunkt t₁ wir betrachten, sondern gilt für beliebige Zeitpunkte  t₁. Folglich läuft die Uhr A mit der Uhr B genau dann synchron, wenn die Uhr B mit der Uhr A synchron läuft, wie behauptet.

Transitivität der Gleichzeitigkeitsdefinition

Angenommen, wir haben es mit drei Uhren A, B und C an drei Orten A, B und C zu tun, und weiter angenommen, Uhr B laufe mit Uhr A synchron, und Uhr C mit Uhr B. Läuft dann auch die Uhr C mit der Uhr A synchron?

Angenommen, jedes unserer Signale benötige für seinen Rundweg von Uhr A zur Uhr B und zurück die Zeit 2·Δt₁, und für den Rundweg von B nach C und zurück nach B die Zeit 2·Δt₂.

Dass Uhr B mit Uhr A synchron läuft, heißt unserer Definition nach, dass ein Signal, welches bei A zu einer beliebigen Zeit t₁ losläuft (Zeit entsprechend der Anzeige von Uhr A), am Ort B zur Zeit t₁ + Δt₁ eintrifft (Zeit entsprechend der Anzeige von Uhr B).

Analog gilt: Dass Uhr C mit Uhr B synchron läuft, heißt unserer Definition nach, dass ein Signal, welches bei B zu einer beliebigen Zeit t₂ losläuft (Zeit entsprechend der Anzeige von Uhr B), am Ort C zur Zeit t₂ + Δt₂ eintrifft (Zeit entsprechend der Anzeige von Uhr C).

Entsprechend der Ableitung im vorigen Abschnitt läuft aber auch Uhr A mit Uhr B synchron, und zwar so, dass ein Signal, welches bei B zu einer beliebigen Zeit t₃ losläuft (Zeit entsprechend der Anzeige von Uhr B), am Ort A zur Zeit t₃ + Δt₁ eintrifft (Zeit entsprechend der Anzeige von Uhr A).

Damit können wir jetzt zum einen sagen, wieviel Zeit ein Signal, welches zum Zeitpunkt t₀ bei A losläuft, dann zu B und anschließend zu C, um auf dem gleichen Weg zurückzukehren, für seine Rundreise benötigt: Zur Zeit t₀ + Δt₁ (Anzeige auf der Uhr B) erreicht es B (da Uhren B und A synchron laufen), vollendet die Teil-Rundreise von B nach C und zurück zur Zeit t₀ + Δt₁ + 2·Δt₂  (auf der Uhr B angezeigt; per obiger Definition der Rundreisezeit von B nach C und zurück) und kommt dann zur Zeit t₀ + 2·Δt₁ + 2·Δt₂ wieder am Ausgangsort A an (angezeigt auf der Uhr A; da Uhr A mit Uhr B synchron läuft).

Zusammengefasst benötigt das Signal für seine Rundreise von A nach C und zurück die Zeit 2·Δt₁ + 2·Δt₂.

Entsprechend können wir bestimmen, wann das Signal, von A kommend, die Uhr C erreicht (angezeigt auf der Uhr C): Läuft es bei der Uhr A zum Zeitpunkt t₀ los, dann erreicht es zum Zeitpunkt t₀ + Δt₁ (Anzeige auf der Uhr B) den Ort B (da Uhren B und A synchron laufen) und als zum Zeitpunkt t₀ + Δt₁+ Δt₂ (Anzeige auf der Uhr C) den Ort C (da die Uhr C mit der Uhr B synchron läuft). Im Vergleich mit der oben angegebenen Rundreisezeit heißt dies aber per Definition, dass die Uhr C mit der Uhr A synchron läuft.

Dementsprechend gilt in der Tat: Läuft die Uhr B mit der Uhr A synchron und die Uhr C mit der Uhr B, dann läuft auch die Uhr C mit der Uhr A synchron. Diese Eigenschaft bezeichnet man als Transitivität. 

 

---

 

2. Originalversion des Blogeintrags 

Gleichzeitigkeit

Am Ende des vorangehenden Teils hatten wir festgestellt, dass wir, um beispielsweise festzustellen, wie viel Zeit die Bewegung eines Objekts von einem Ort A zu einem anderen Ort B benötigt, ein Verfahren zur Synchronisation zweier in A und in B befindlicher Uhren benötigen oder, anders ausgedrückt, ein Verfahren um festzustellen, welche Ereignisse in A und in B gleichzeitig stattfinden.

Nur so konnten wir feststellen, welche Zeit unser Körper für seine Reise von A nach B benötigt hat. Verkürzt gesagt: Wenn wir in A und B jeweils eine Uhr aufstellen, können wir zwar direkt auf der A-Uhr ablesen, wann der Körper (unten als grüne Kugel dargestellt) am Ort A losgeflogen ist, und auf der B-Uhr, wann er am Ort B angekommen ist:

Aber wenn die A-Uhr und die B-Uhr nicht synchronisiert sind und wir nicht wissen, wie sich die Zeitanzeigen dieser beiden verschiedenen Uhren zueinander verhalten, können wir nichts über die Reisezeit des Körpers sagen. [Beispiele]

Um Gleichzeitigkeit zu definieren und Uhren miteinander zu synchronisieren gibt es zwei einfache Vorgehensweisen: Synchronisation mit Hilfe von Signalen und Synchronisation durch Uhrentransport.

Synchronisation mit Hilfe von Signalen

Nehmen wir an, ich habe zwei Uhren, die ich synchronisieren möchte: eine am Ort A, eine am Ort B. Ein Ansatz zur Synchronisation könnte darin bestehen, dass ich zwischen den Uhren eine Telefonleitung verlege:

Dann postiere ich mich bei einer der Uhren, einen Helfer bei der anderen, und ich sage meinem Helfer per Telefon durch, was die neben mir stehende Uhr gerade anzeigt. Der Helfer kann die neben ihm stehende Uhr so stellen, dass die Anzeige seiner Uhr und meine Zeitansage genau übereinstimmen.

Ist uns der Umweg über die menschliche Stimme und das per-Hand-Einstellen zu kompliziert und fehleranfällig und wollen wir größere Genauigkeit erreichen, dann können wir stattdessen eine elektronische Regeleinheit einsetzen, die automatisch die Anzeige der einen Uhr abliest und das Ergebnis per Telefonleitung zu einer automatische Stelleinheit neben der zweiten Uhr überträgt, wo die Stelleinheit den Zustand der zweiten Uhr entsprechend anpasst.

Für die meisten Alltagsbedürfnisse ist das ein praktikables Verfahren. Genau so funktioniert die telefonische Zeitansage. Vereinfacht gesagt (genauere Informationen z.B. hier) gilt: Neben den hochgenauen Atomuhren der Physikalisch-Technischen Bundesanstalt sitzt ein Computer, der diese Uhren abliest und daraus telefonische Ansagen bastelt: “Beim nächsten Ton ist es 11 Uhr, eine Minute und zehn Sekunden. Piep.” Nach diesen Ansagen kann ich als Anrufer dann z.B. meine Armbanduhr stellen.

Um welche Art von Signal es sich handelt, möchte ich in diesem Stadium bewusst offen lassen. Später, im Rahmen der Speziellen Relativitätstheorie, werden Lichtsignale die entscheidende Rolle spielen. Im Prinzip ist aber jedes Signal geeignet, solange es bestimmte Eigenschaften erfüllt, auf die ich unten noch genauer eingehen werde.

Beißt sich da eine Katze in den Schwanz?

Bei genauerer Betrachtung birgt das hier beschriebene Verfahren eine grundlegende Schwierigkeit. Die telefonische Übertragung von Information mag zwar, gemessen an typischen Geschwindigkeiten, die wir aus dem Alltag gewohnt sind, extrem schnell sein. Aber eine winzige Verzögerung gibt es dennoch: Zwischen dem Moment, in dem ich meine Zeitsage ins Telefon spreche und dem Moment, in dem mein Helfer die Zeitansage hört, vergeht ein wenig Zeit. Auch unsere automatisierte Version kann das nicht völlig ausschalten, denn auch in diesem Falle kommt es mindestens deswegen zu einer Verzögerung, weil ein elektrisches Signal die Telefonleitung entlang läuft und ein wenig Zeit benötigt, um von A nach B zu gelangen.

Wüsste ich z.B., dass das Signal die Telefonleitung entlang mit konstanter Geschwindigkeit v von A nach B läuft, dann könnte ich diesen Effekt berücksichtigen. Ich müsste dazu nur die Länge L der Telefonleitiung messen, die A und B verbindet, und wüsste dann: Ein Signal, das den Ort A zur Zeit t₀ verlässt, erreicht den Ort B zur Zeit t₀ + L/v. Der letzte Term, L/v, ist schlicht die Laufzeit Δt des Signals: die Länge des Kabels L, durchlaufen mit der konstanten Geschwindigkeit v, das heißt L = v· Δt oder eben, nach Δt aufgelöst, Δt = L/v. Hier ist das Ganze schematisch dargestellt:

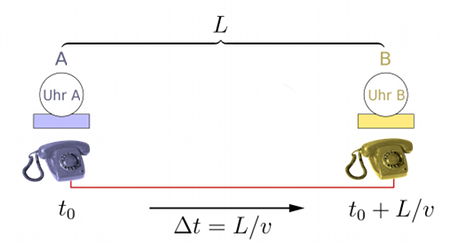
Sprich: In dem Moment, in dem das Signal “Uhr A zeigt 12:00 Uhr” bei der Uhr B ankommt, sollten wir die Uhr B nicht auf 12:00 Uhr stellen, sondern auf 12:00 Uhr plus Δt. Das berücksichtigt, dass uns die um 12:00 Uhr losgeschickte Ansage eben nicht instantan um 12:00 Uhr erreicht, sondern um Δt später.

Doch wie können wir überhaupt feststellen, dass das Signal die Telefonleitung mit konstanter Geschwindigkeit v entlangläuft, und wie können wir den Wert von v bestimmen? Das ist nicht so einfach, wie man auf den ersten Blick meinen könnte. Wir hatten eingangs schließlich festgestellt: Um messen zu können, wieviel Zeit ein Objekt benötigt, um sich von A nach B zu bewegen, benötigen wir bereits zwei miteinander synchronisierte Uhren, nämlich eine am Ort A, die andere am Ort B. Wie können wir diese Information, nämlich die Laufzeit des Signals von A nach B, denn dann benutzen, um überhaupt festzustellen, ob unsere Uhren synchron laufen oder nicht? Beisst sich die Katze hier in den Schwanz?

Signal auf Rundwegen

Fast, aber nicht ganz. Machen wir einmal folgendes: Wir senden nicht nur ein Signal von A nach B, sondern wir senden ein Signal hin und zurück; sobald das Signal den Ort B erreicht hat, senden wir sofort ein gleichartiges Signal von B zurück nach A. Dann können wir mit einer einzigen Uhr, nämlich der Uhr am Ort A, feststellen, wieviel Zeit das Signal für seinen Rundweg benötigt hat. Damit können wir zumindest einen wichtigen Teil der Eigenschaften einer konstanten Signalgeschwindigkeit direkt prüfen: Bei konstanter Geschwindigkeit v entlang des Rundweges sollte das Signal für Hin- plus Rückreise entlang eines Weges der Länge L die Zeit 2·L/v benötigen. Messen wir für Rundwege möglichst vieler verschiedener Längen L die benötigte Laufzeit und erhalten immer den Wert 2·L/v, dann hat unsere Annahme einer konstanten Geschwindigkeit bereits einen wichtigen Test bestanden.

Allerdings haben wir bei Rundwegen definitionsgemäß niemals Hin- und Rückweg getrennt betrachtet. Das müssen wir jetzt nachholen. Sind Hin- und Rückweg des Signals völlig gleichberechtigt, dann liegt die Annahme nahe, dass das Signal für Hin- und Rückweg jeweils gleich viel Zeit benötigt hat, nämlich genau die Hälfte der Zeit, die es für den Rundweg benötigte. 

Um sicherzustellen, dass Hin- und Rückweg tatsächlich gleichberechtigt sind und sich der Lauf des Signals von A nach B möglichst wenig vom Lauf von B nach A unterscheidet, treffen wir alle nur erdenklichen Vorkehrungen: Wir eliminieren so weit wie möglich alle Störfaktoren und gestalten die Signalübertragung so richtungsunabhängig, wie wir es nur vermögen. Beispielsweise sollten wir für unsere Signalübertragung in beide Richtungen das gleiche oder zumindest baugleiche, direkt nebeneinander verlegte Kabel benutzen, baugleiche Sender am Ort A und am Ort B, und so weiter und so fort. Auch der Verlauf des Übertragungsweges sollte symmetrisch gewählt sein; eine naheliegende Wahl ist es, das Signal auf direktem Wege von A nach B bzw. zurück laufen zu lassen.

Isotropie, Homogenität und die Naturgesetze

Ein Umstand könnte uns jetzt noch einen Strich durch die Rechnung machen. Wären die physikalischen Gesetze, die bei der Signalübertragung eine Rolle spielen, richtungsabhängig und würden insbesondere eine Bewegung von A nach B anders behandeln als eine Bewegung von B nach A, dann könnten wir uns noch so sehr bemühen, Hin- und Rückweg des Signals möglichst gleich zu gestalten; wir könnten doch nicht sicherstellen, dass Hin- und Rückreise gleich lange dauern. Der Unterschied zwischen Hin- und Rückweg wäre dann in den physikalischen Gesetzen selbst festgeschrieben. Das könnte bedeuten, dass entweder nicht alle Raumrichtungen gleichberechtigt sind – z.B. könnten sich unsere Signale entlang einer “fundamentalen Richtung des Raums” schneller bewegen als entgegengesetzt zu dieser Richtung. Oder aber es heißt, dass nicht alle Orte im Raum gleichberechtigt sind. Das könnte sich darin äußern, dass Signale zu bestimmten Orten schneller hin- und von dort langsamer zurückfliegen. Zu allem Überfluss könnte sich im Prinzip auch noch eine Zeitabhängigkeit einschleichen; die könnte sich darin äußern, dass Signale zu verschiedenen Zeiten – und damit z.B. auch bei einer auf eine Hinreise folgenden Rückreise – unterschiedlich schnell laufen.

Zeigen die physikalischen Gesetze keine Richtungsabhängigkeit, nennt man dies Isotropie; zeigen sie keine Abhängigkeit vom Ort, spricht man von Homogenität des Raums. Dass die physikalischen Gesetze jederzeit in der gleichen Weise gelten und dass das Verhalten der Objekte keinen Zeitpunkt vor irgendeinem anderen Zeitpunkt auszeichnet, heißt Homogenität der Zeit.

Die Annahme, dass die physikalischen Gesetze nicht richtungsabhängig und nicht ortsabhängig und nicht explizit zeitabhängig sind, also keine Raumrichtung vor den anderen Richtungen und keinen Ort im Raum vor anderen Orten auszeichnen, lässt sich in vielfältiger Weise mit Experimenten auf die Probe stellen, die keine synchronisierten Uhren voraussetzen.

Ein sehr spezifisches Beispiel dafür hatten wir bereits kennengelernt, nämlich die Messung, wie viel Zeit ein Signal benötigt, um eine gerade Strecke der Länge L hin- und wieder zurück zu fliegen. Führt man dieses Experiment an verschiedenen Orten durch – äußere Einflüsse müssen natürlich, wie immer bei solchen Experimenten, hinreichend effektiv abgeschirmt werden -, dann kann man auf diese Weise die Ortsabhängigkeit der Gesetze testen, welche die Eigenschaften der Signalausbreitung bestimmen. Mithilfe unterschiedlicher Orientierungen der geraden Teststrecke, auf der man das Signal hin- und wieder zurücklaufen lässt, kann man auch die Richtungsabhängigkeit der Gesetze testen.

Die meisten Tests von Isotropie und Homogenität laufen ab, ohne, dass es den Experimentatoren überhaupt bewusst wäre. Sobald jemand irgendwo in einem irdischen Laboratorium ein Experiment durchführt, das zu einem späteren Zeitpunkt von ihm/ihr selbst, einem Kollegen oder einer Kollegin wiederholt wird, ist dies auch ein Test von Isotropie und Homogenität: Da sich die Erde zum einen um ihre eigene Achse dreht und sich zum anderen durch den Raum bewegt (auf ihrer Bahn um die Sonne, mit der Sonne durch unsere Milchstraße, mit der Milchstraße gegenüber den anderen Galaxien) finden solche Wiederholungen an einem anderen Ort im Raum statt als das Originalexperiment, und die Apparaturen sind selbst bei Wiederholungen, die im gleichen Labor stattfinden, in eine andere Richtung ausgerichtet.

Dass solche Wiederholungen in so überwältigend vielen Fällen funktionieren, ohne, dass die Wissenschaftler Ort und Ausrichtung des Experiments in ihre Analyse einbeziehen müssten, ist ein starker Hinweis auf eine den Naturgesetzen innewohnende Isotropie und Homogenität. Auf direkte experimentelle Tests insbesondere mit Bezug auf die für die Spezielle Relativitätstheorie so wichtige Lichtausbreitung werde ich in späteren Abschnitten von Einstein verstehen noch eingehen. Bei der Formulierung von Isotropie und Homogenität und verwandten Eigenschaften der Naturgesetze (“Invarianzen”) gibt es einige Subtilitäten und weitere Überlegungen, die uns ebenfalls später noch beschäftigen werden.

Alternative Rundwege

Nach unseren Annahmen (möglichst symmetrische Einrichtung des Rundweges, Homogenität und Isotropie der Naturgesetze) ist sehr plausibel, dass unser Signal auf dem Weg von A nach B gerade die Hälfte der Zeit benötigt wie für den Rundweg ABA, hin und zurück.

Es gibt eine weitere Art von Test, die diese Plausibilität noch weiter unterfüttert. Dazu betrachten wir unterschiedliche Wege, auf denen wir unser Signal von A nach B schicken können; hier sind rot und blau zwei verschiedene Möglichkeiten eingezeichnet:

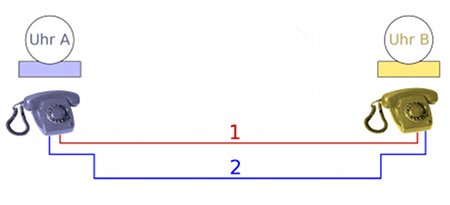
Nehmen wir an, das Signal benötige auf dem Weg 1 hin und zurück von A nach B nach A die Zeit 2·Δt₁, und auf dem Weg 2 für die Reise von A nach B zurück nach A die Zeit 2·Δt₂. Wenn wir annehmen, dass auf Hin- und Rückweg jeweils die gleiche Zeit entfällt, dann sollte ein Signal, das wir auf dem Weg 1 von A nach B, aber auf dem Weg 2 wieder zurück von B nach A schicken, dazu insgesamt die Zeit Δt₁ + Δt₂ benötigen. Ob dies tatsächlich zutrifft, können wir aber auch ohne Gleichzeitigkeitsdefinition messen, denn Start und Ankunft des Signal finden ja, weil es sich um einen Rundweg handelt, am gleichen Ort statt. Die Messung erfolgt nur auf der Uhr A, am Ort A.

Wir können noch viele weitere solche alternativen Rundwege bauen, und wir können die Messungen anstatt am Ort A auch am Ort B stattfinden lassen  (dann wird zur Messung nur die baugleiche Uhr B verwendet). Wenn sich bei all diesen alternativen Rundwegmessungen jeweils ergibt, dass die Rundwegzeit die erwartete Summe der “Teilzeiten” ist (bei “Weg 1 hin, Weg 2 zurück” eben Δt₁ + Δt₂), und wenn wir auch bei noch mehr Wegen 3, 4, 5, … mit assoziierten Zeiten Δt_3, Δt_4, Δt_5, … experimentell feststellen, dass bei allen möglichen Rundwegkombinationen immer dann, wenn das Wegstück n einfach durchlaufen wird, auch der Term Δt_n in der Summe auftaucht, und die Summe direkt aus den entsprechenden Δt-Beiträgen aller durchlaufenen Wegstücke besteht, dann ist es in der Tat plausibel, mit jedem der Teilstücke die entsprechende Einweg-Reisezeit zu assoziieren (z.B. mit jedem Durchlaufen des Wegstücks 1 eben die Reisezeit Δt₁).

Isoliert messen können wir die Einweg-Reisezeiten für jedes Teilstück damit nach wie vor nicht – da wir immer Rundwege betrachten, ist die Einweg-Reisezeit immer teil einer Summe aus mehreren Komponenten. Dass wir die Einweg-Reisezeiten mit den Wegstücken assoziieren, ist und bleibt eine Konvention, die eine Definition der Gleichzeitigkeit einschließt. Aber es handelt sich um eine Konvention, die nach erfolgreicher Durchführung dieser Messungen der alternativen Rundwege erheblich an Plausibilität gewinnt.

Jetzt aber: Gleichzeitigkeit

Nach diesen Vorüberlegungen haben wir jetzt alle Elemente beisammen, um mit Hilfe von Signalausbreitung Gleichzeitigkeit zu definieren.

Als erstes benötigen wir Signale, die wir – sei es mit Hilfe von Leitungen, sei es, wie bei Licht, direkt – Hin- und Hersenden können. Wir verwenden dabei nur Signale, für die wir soweit wie möglich durch Messungen sichergestellt haben, dass ihre Ausbreitungsgesetze die Homogenität von Raum und Zeit und die Isotropie des Raumes respektieren, sprich: für deren Ausbreitung es keine durch die Naturgesetze festgelegte Richtungs-, Zeit- oder Ortsabhängigkeit gibt. Wir stellen durch die Art und Weise, wie die Signale von einem Ort zum anderen übermittelt werden, so gut wie möglich sicher, dass Hin- und Rückreise für diese Signale so gleich wie möglich verlaufen.

Als Kontrolle dienen uns dabei die oben beschriebenen Messungen mit “alternativen Rundwegen”; wir verwenden nur Signale, für die jeweils gilt: Gegeben zwei Wege 1 und 2, auf denen das Signal von einem Ort zum anderen hin- und dann wieder zurücklaufen kann, und angenommen, dass ein Hin-und-Zurücklaufen entlang Weg 1 die Zeit  2·Δt₁, und auf dem Weg 2 die Zeit 2·Δt₂ benötigt, dann benötigt ein Hinlaufen entlang des Weges 1 plus Zurücklaufen entlang des Weges 2 die Zeit Δt₁ + Δt₂ (“Eigenschaft der alternativen Rundwege”).

Zwischenbemerkung: Im Gegensatz zu den Überlegungen weiter oben geht an dieser Stelle nirgends ein, dass sich die Signale auf Rundwegen mit konstanter Geschwindigkeit bewegen. Wir setzen ebenfalls nicht voraus, dass es sich nur um eine Art von Signal handelt; es kann sich durchaus um mehrere verschiedene Signalarten handeln. Ein “alternativer Rundweg” kann z.B. auch darin bestehen, dass ein elektrisches Signal entlang einer elektrischen Leitung von A nach B läuft (Weg 1), und ein Lichtsignal direkt von B nach A zurück (Weg 2).

Mit Hilfe dieser Signale definieren wir die Synchronizität von Uhren (und damit die Gleichzeitigkeit) nun wie folgt: Benötigt ein Signal der von uns verwendeten Sorte auf der Rundreise von Uhr A zur Uhr B und entlang desselben Weges zurück die (auf Uhr A gemessene) Zeit 2·Δt, dann gehen die beiden Uhren genau dann synchron wenn gilt: Läuft zum Zeitpunkt t₀ (laut Anzeige auf der Uhr A) ein Signal auf dem gegebenen Weg zur Uhr B, dann zeigt die Uhr B bei der Ankunft des Signals den Zeitpunkt t₀ + Δt an.

Dank der Eigenschaft der alternativen Rundwege sind die verschiedenen Möglichkeiten, diese Definition umzusetzen zueinander äquivalent. Es lässt sich außerdem direkt nachprüfen, dass diese Definition der Gleichzeitigkeit entscheidende weitere Anforderungen erfüllt, die man an dieses Konzept stellen sollte: Läuft Uhr B mit Uhr A synchron, dann sollte auch Uhr A mit Uhr B synchron laufen (Symmetrie). Und wenn Uhr A mit Uhr B synchron läuft, und Uhr B mit Uhr C synchron läuft, dann läuft auch die Uhr A mit der Uhr C synchron (Transitivität). [Details]

Synchronisation mit Signalen ist die Grundlage der offiziellen Weltzeit. Wenn Sie derzeit vor einem Computer sitzen, ist dieses Verfahren auch mit einiger Wahrscheinlichkeit die Art und Weise, wie sich Ihr Computer die genaue Zeit verschafft — bei einem komplexeren Rechner mittels des Network Time Protocol, eines der Standard des Internet Protocol, mit einer Genauigkeit besser als 10 Millisekunden, bei einer alleinstehenden Windows-Maschine mittels des nur auf einige Sekunden genauen Windows Time Service. Die Signalübertragung erfolgt dabei über das Internet. Im Prinzip stellt der Computer dabei mit Hilfe der Hin- und Rückreisezeiten von Datenpaketen fest, wie lange Signale von ihm selbst zum Referenzcomputer, der an eine Atomuhr angeschlossen ist, laufen, und er korrigiert die eintreffenden Zeitsignale des Referenzcomputers entsprechend. In der Praxis muss der Computer berücksichtigen, dass es unterschiedliche Übertragungswege gibt, die (sogar je nach Reisezeitpunkt!) unterschiedlich schnell sein können; er kombiniert daher die Informationen von mehreren Referenzcomputern in geschickter Weise, um die tatsächliche Synchronisation so gut wie möglich abzuschätzen.

Kommen wir jetzt zum zweiten Verfahren, der

Synchronisation durch Uhrentransport

Für dieses Verfahren setzen wir neben den Uhren A und B, die wir synchronisieren wollen, eine dritte Uhr R ein: die “Reiseuhr”. Zunächst befindet sich die Reiseuhr am Ort A. Dort kann sie direkt mit Uhr A synchronisiert, sprich: auf die gleiche Zeit wie Uhr A eingestellt werden:

In der einfachsten Version des Synchronisationsverfahren transportieren wir die Uhr R dann an den Ort B, und dann wird Uhr B direkt am gleichen Ort mit der Uhr R synchronisiert. Sind Uhr B und Uhr A damit sinnvoll synchronisiert?

Uhrentransporte führen wir im Alltag gerne und oft durch: Wir bringen zwei zu synchronisierende Uhren, z.B. unsere Armbanduhr und eine Referenzuhr, an ein und denselben Ort, stellen vor Ort sicher, dass die Uhren in der Tat synchron gehen, also jeweils gleichzeitig die gleiche Zeit anzeigen, und verbringen die Uhren anschließend wieder an ihre unterschiedlichen Einsatzorte. In der Regel bleibt die Referenzuhr dabei, wo sie ist, und wir verlassen uns darauf, dass unsere Armbanduhr überall dort, wohin wir sie mittragen, die richtige Zeit anzeigt.

Doch woher wissen wir eigentlich, dass die Bewegung den Gang der Uhren nicht beeinflusst, und dass unsere Synchronisation dadurch, dass wir die Uhr von einem Ort an den anderen bringen, nicht wieder zunichte gemacht wird?

Eine Möglichkeit, den Uhrentransport auf die Probe zu stellen, besteht darin, dass wir die eine Uhr nach der Synchronisation mit der Referenzuhr nicht zu einem anderen Ort, sondern auf einem Rundweg transportieren. Dann befinden sich die beiden Uhren per Definition nach Abschluss des Transports wieder an ein und demselben Ort, und wir können direkt vergleichen, ob sie immer noch synchron laufen. Tun sie dies nicht mehr – und wir sollten uns bei dieser Aussage nicht auf eine einzige Transportweise verlassen, sondern verschiedene Wege und Transportweisen vergleichen – oder, alternativ, zeigen auf verschiedene Weise von A nach B transportierte Reiseuhren dort, also am Ort B, unterschiedliche Zeiten an, dann müssen wir noch einen Schritt weiter gehen.

Synchronisation mit Hin- und Rücktransport

Ein Ausweg ist es dann, folgendermaßen vorzugehen – und der Leser wird eine direkte Analogie mit der Uhrensynchronisation durch Signalübertragung bemerken: Wir bemühen uns, Hin- und Rückweg soweit, wie es uns möglich ist, gleich zu gestalten: Wir benutzen die gleichen Transportmittel (z.B. das gleiche Auto oder die gleiche Rakete), den gleichen Transportweg (z.B. die gleiche Fahrstrecke) und einen soweit wie möglich gleichen Transportverlauf (Gasgeben/Bremsen bzw. Düsenschubänderungen finden relativ zum Transportbeginn nach der gleichen, auf der mitgeführten Uhr gemessenen Zeit statt).

Außerdem betrachten bis auf weiteres relativ zueinander ruhende Uhren A und B, deren Abstand voneinander sich also nicht verändert; so sind Hin- und Rückweg auf alle Fälle gleich lang. Alle Einflüsse, von denen wir sonst noch annehmen, dass sie den Uhrenverlauf beeinflussen könnten, bemühen wir uns so weit wie möglich auszuschalten. Wir lagern die Reiseuhr beispielsweise so, dass ihr Lauf möglichst wenig durch Ruckeln, Magnetfelder oder ähnliches gestört wird.

Allerdings haben wir dann immer noch das gleiche potenzielle Problem wie bei der Uhrensynchronisation durch Signale. Es könnte wiederum sein, dass die physikalischen Gesetze selbst richtungs-, orts- oder zeitabhängig sind und dafür sorgen, dass sich die Uhr beim Transport von A nach B anders verhält als beim Transport in die Gegenrichtung, von B zurück nach A. Aber, wie schon gesagt: Entsprechende Experimente zeigen keine solche grundsätzliche Richtungs- oder Ortsabhängigkeit. Wir gehen daher wiederum davon aus, dass wir Isotropie und Homogenität der physikalischen Gesetze annehmen können.

Das motiviert die folgende Synchronisationsvorschrift durch Uhrentransport: Wir lassen unsere Reiseuhr R zunächst eine Rundreise absolvieren. Dazu wird die Uhr zuerst am Ort A mit der Uhr A synchronisiert. Dann reist sie an den Ort B, und wir stellen die dort befindliche Uhr provisorisch so ein, dass sie während des Aufenthaltes der Reiseuhr R mit jener synchron läuft:

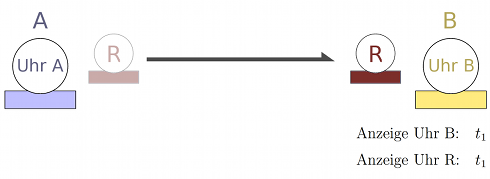
Anschließend reist die Uhr R zurück an den Ort A, wobei wir Hin- und Rückreise soweit wie irgend möglich gleich gestalten und von äußeren Einflüssen abschirmen. Nachdem die Reiseuhr wieder an ihren Ausgangspunkt A zurückgekehrt ist, vergleichen wir ihre Anzeige ein weiteres Mal mit der Anzeige der Uhr A.

Angenommen, beim erneuten Vergleich der beiden Uhren R und A am Ort A wichen die Anzeigen der beiden Uhren um Δt voneinander ab:

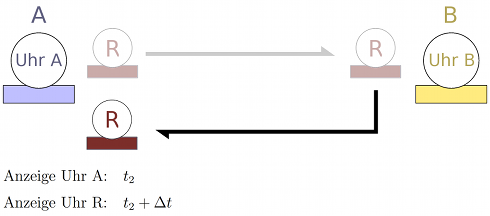
Offenbar hat sich für die Uhr R gegenüber der Uhr A auf ihrer Rundreise eine Differenz Δt ergeben (die, je nach dem Vorzeichen von Δt, bedeuten kann, dass Uhr R insgesamt schneller oder langsamer gegangen ist als Uhr A). Nun haben wir allerdings alles dafür getan, dass Hin- und Rückreise in möglichst gleicher Weise verlaufen sind; außerdem haben wir vorausgesetzt, dass auch die physikalischen Gesetze Hin- und Rückreise gleich behandeln (Orts- und Richtungsunabhängigkeit).

Vor diesem Hintergrund ist die Annahme naheliegend, dass die Uhr R, als sie die Hälfte ihrer Reise hinter sich hatte – nämlich bei der Ankunft der Uhr R bei Uhr B – die halbe Differenz zu Uhr A aufgewiesen hat, also Δt/2. Entsprechend wählen wir unsere Definition der Gleichzeitigkeit, basierend auf der Synchronisation durch Uhrentransport: Wir stellen die Anzeige der Uhr B, die wir ja zunächst vor Ort mit der Uhr R synchronisiert hatten, um Δt/2 zurück; in diesem Zustand ist die Uhr B dann gemäß unserer Definition mit der Uhr A synchronisiert.

Bis zu den 1970er Jahren war im Rahmen der Messgenauigkeit der besten Uhren bei vorsichtigem Transport kein Rundreise-Gangunterschied Δt nachzuweisen. Darauf, dass dies mit modernen Atomuhren möglich ist, werden wir später – dann schon im Rahmen der Speziellen Relativitätstheorie, die solche Phänomene voraussagt – zurückkommen. Unsere Synchronisierungsvorschrift mit Hilfe von Uhrentransport ist in beiden Fällen eine mögliche Wahl; in der klassischen Physik ebenso wie später in der Speziellen Relativitätstheorie.

Schluss

Dazu, inwieweit die zwei Gleichzeitigkeitsdefinitionen, die wir in diesem Teil vorgestellt haben, gleichwertig sind, mache ich an dieser Stelle keine Aussage; auf diese Frage werden wir ebenfalls in einem späteren Teil zurückkommen.

Zumindest für die praktischen Anwendungen im Rahmen des Gültigkeitsbereichs der klassischen Mechanik macht es keinen Unterschied, welche der Definitionen wir wählen. Tatsächlich ist die klassische Mechanik lange Zeit gut damit gefahren, sich über solche Definitionen keine weitergehenden Gedanken zu machen; der erste, der sich des grundlegenden Problems angenommen hat, scheint Henri Poincaré mit einem 1898 erschienenen Aufsatz gewesen zu sein (vgl. S. 23f. in Giulini 2005). Lichtlaufzeiten hatten allerdings schon deutlich vorher für die berühmten Beobachtungen von Ole Römer eine Rolle gespielt: Römer hatte 1675 die Umläufe der Jupitermonde beobachtet; will man irdische Beobachtungen dieser Umläufe genau vorhersagen, muss man berücksichtigen, dass das Licht eine gewisse Zeit benötigt, um uns vom Jupiter aus zu erreichen, und dass sich diese Lichtlaufzeitverzögerung je nach aktuellem Erde-Jupiter-Abstand ändert. Aus diesen Beobachtungen konnte Römer eine Untergrenze für die Lichtgeschwindigkeit abschätzen. 

Die moderne Version des Römer’schen Problems ergibt sich, wenn Astronomen Beobachtungen vornehmen, bei deren Auswertung Zeitabläufe mit großer Genauigkeit rekonstruiert werden sollen. Ein modernes Beispiel sind Messungen der Radialgeschwindigkeiten von Sternen, aus denen sich auf die Anwesenheit von Planeten um diese Sterne (“Exoplaneten”) schließen lässt. Je nachdem, wo sich die Erde auf ihrer Bahn befindet, kommt das Licht des Sterns ein paar Minuten früher oder später an. In der Praxis wird dieser Störeffekt herausgerechnet (Baryzentrisches Julianisches Datum); andernfalls würde er die Ergebnisse empfindlich verfälschen.

Ein jüngstes Anwendungsbeispiel für unsere Überlegungen zur Synchronisierung mit Hilfe von Signalen könnten die Messungen überlichtschneller Neutrinos sein. Dort ist ja seit Ende Februar eine problematische Steckverbindung im Gespräch, die die Abschätzung der Signal-Reisezeit – und damit die Ermittlung der Geschwindigkeit der Neutrinos auf ihrem Weg von A nach B – verfälscht haben könnte.

Die praktischen Aspekte des Uhrentransports haben historisch (insbesondere im Vergleich zu den grundlegenden Überlegungen) eine sehr wichtige Rolle gespielt, und zwar im Rahmen des so genannten Längenproblems.  Seeleute können durch Vergleich der Anzeige einer mitgeführten präzisen Uhr mit astronomischen Beobachtungen ihre geographische Länge bestimmen; allerdings nur, wenn die mitgeführte Uhr trotz des Schaukelns und der Belastungen einer Seereise hinreichend genau mit den auf Land stationierten Referenzuhren synchron läuft (das bekannteste populärwissenschaftliche Buch zu diesem Thema ist Dava Sobel, Längengrad. Berlin Verlag: 2000).

Im Rahmen der Speziellen Relativitätstheorie kann man allgemein nachweisen, dass die beiden Definitionen der Gleichzeitigkeit (und alle anderen Definitionen, die bestimmte vernünftige allgemeine Voraussetzungen erfüllen) äquivalent sind; dazu siehe Giulini 2000. Die dort angewandten Beweisverfahren gehen allerdings weit über das Niveau dieser einfachen Einführung hinaus.

Nach diesem Einschub zur Gleichzeitigkeitsdefinition kehren wir im folgenden Teil IV zu den Gesetzen der klassischen Mechanik zurück, die ich bereits in Teil I, dort allerdings ohne die nötigen Grundlagen, kurz beschrieben hatte.

---

 

3. Nicht auf der Hauptseite veröffentlichte Kommentare

Im Gegensatz zu meinem Vorgehen bei Teil I und Teil II finden sich die nicht auf der Hauptseite veröffentlichten Kommentare nicht hier, sondern auf einer externen Seite, nämlich hier auf einer Unterseite meiner Webseiten am AEI.