Eine Sekunde, bitte! Teil I: Astronomie
BLOG: RELATIV EINFACH

Wie das so ist mit dem Bloggen: Ein Thema führt zum nächsten. Bei der Recherche für meinen letzten Blogeintrag, indem es ja um die Frage ging, was eine gute Maßeinheitendefinition auszeichnet, habe ich mich zwischenzeitlich bei der wechselhaften (aber immer nur im Rahmen der Messgenauigkeit!) Geschichte der grundlegenden Maßeinheiten festgelesen. Insbesondere an einem der Handvoll von Beispiele, die jeder aus dem Alltag kennt: der Sekunde.
Tagein, tagaus
Die Sonne geht auf, erreicht gen Mittag ihren höchsten Stand und geht anschließend wieder unter. Wieder ein Tag vorbei, genauer gesagt: ein “ganzer Tag”, im Gegensatz zum “lichten Tag”, einer weiteren Bedeutung des Wortes Tag, der Zeitspanne zwischen Sonnenaufgang und Sonnenuntergang (also: ganzer Tag gleich lichter Tag plus Nacht).
Das ist die wohl natürlichste Zeitunterteilung, die wir kennen. Da der Tag aber nun doch eine eher längere Zeiteinheit ist, liegt es nahe, ihn zu unterteilen, zum Beispiel: Den lichten Tag und die Nacht in jeweils 12 gleiche Teile, Stunden genannt; den ganzen Tag also in 24 Stunden.
Das Problem: Lichte Tage sind nicht immer gleich lang; im Sommer sind sie länger als im Winter, und wenn man den Polen der Erde genügend nahe kommt, kann der lichte Tag im Sommer ein halbes Jahr dauern. Nimmt man eine Zwölftelung von lichtem Tag und Nacht vor, um Stunden zu definieren, dauern diese Stunden dementsprechend je nach Jahreszeit deutlich unterschiedlich lange. Solche so genannten temporalen Stunden mögen für verschiedene Alltagszwecke recht praktisch sein, und sowohl im alten Ägypten als auch im klassischen Griechenland hat es wohl solch eine Einführung gegeben.
Dass man im Winter in einer temporalen Stunde deutlich weniger Arbeit erledigen kann als im Sommer wird den Menschen bereits vor Erfindung von Uhren aufgefallen sein. In Heidelberg beispielsweise ist der lichte Tag im Winter nur rund 8 mit der Uhr gemessene Stunden lang, im Sommer rund doppelt so lang. Auch die alten Griechen waren sich dieser Unterschiede, und sogar ihrer Abhängigkeit vom Beobachtungsort, bereits bewusst.
Die folgende schöne Grafik, die ich auf Wikipedia gefunden habe, zeigt die jährlichen Variationen der Länge des lichten Tages in Abhängigkeit vom Breitengrad; mit “Stunden” sind in dieser Grafik natürlich nicht temporale Stunden gemeint, sondern die üblichen, jeweils gleich langen Stunden, auf die wir später noch kommen werden und die z.B. unsere üblichen Armband- oder Handyuhren anzeigen:
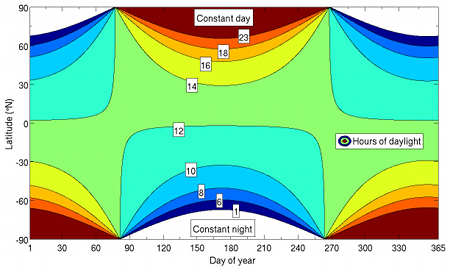
Zu lesen ist das Diagramm, das ein freundlicher Mensch mit Benutzernamen Jalanpalmer aus dieser Gleichung erstellt hat, wie folgt: Man nehme die geographische Breite des eigenen Ortes, in meinem Falle Heidelberg auf rund 50 Grad nördlicher Breite. Auf der y-Achse sind die geographischen Breitenwerte eingetragen; male ich für Heidelberg beim Wert 50 eine horizontale Linie in das Diagramm, dann kann ich von links nach rechts über das Jahr hinweg ablesen, wie lang der entsprechende lichte Tag ist: zu Jahresbeginn schneidet meine Linie die Grenzregion zwischen Hellblau und nicht ganz so hellem Blau, entsprechend einer winterlichen Taglänge von etwa 8 Stunden. Im Sommer dagegen führt die Linie in die Grenzregion von gelbgrün und orange, entsprechend einer sommerlichen Taglänge von rund 16 Stunden.
Wie diese Variationen zustandekommen, kann sich jeder klarmachen, der weiss, wie die Jahreszeiten entstehen: Im Sommer ist unsere Halbkugel zur Sonne hin geneigt; der Kreisbogen, den unser Beobachtungsort im Laufe einer Umdrehung beschreibt, liegt daher zum größeren Teil im Sonnenlicht und nur zu einem geringeren Teil im Erdschatten.
Also, weg mit den temporalen Stunden. Wie ist es, wenn wir stattdessen den ganzen Tag einheitlich in 24 Stunden einteilen? Das sollte das Problem der jahreszeitlichen Variation der (lichten) Taglänge beheben.
Sonnentag und äquinoktiale Stunden
Die Stunden der 24-Stunden-Einteilung des ganzen Tages und die temporalen Stunden sind an zwei Tagen im Jahr in sehr guter Näherung gleich lang: Zur Tagundnachtgleiche, die zum einen jeweils um den 20. März, zum anderen um den 23. September herum liegt und, wie der Name schon sagt, dadurch definiert ist, dass zu diesem Zeitpunkt lichter Tag und Nacht so gut wie die gleiche Länge haben. Der Fachbegriff für die Tagundnachtgleiche ist Äquinoktium, und die 24 Stunden, die den ganzen Tag gleichmäßig unterteilen, heißen dementsprechend äquinoktiale Stunden.
Genauer gesagt sind diese Stunden so definiert: Ein Sonnentag entspricht einem vollständigen Umlauf der Sonne um die Erde. Man könnte ihn beispielsweise über die Zeitpunkte messen, an denen die Sonne am Beobachtungsort ihren höchsten Stand am Himmel erreicht, den “lokalen Mittagen”, und den Sonnentag als Zeitraum zwischen einem lokalen Mittag und dem nächsten definieren, also sozusagen von 12 Uhr lokaler Zeit bis zu 12 Uhr lokaler Zeit. Die Astronomen haben den Sonnentag stattdessen von 0 Uhr bis 0 Uhr definiert, also den nicht sichtbaren Tiefststand der Sonne als Ausgangspunkt genommen.
Doch auch die Länge des Sonnentags variiert über das Jahr hinweg ein wenig. Die Variation ist bei weitem nicht so groß wie für den lichten Tag; sie beträgt lediglich bis zu einer halben Minute. Hat man aber erst einmal hinreichend genau gehende Uhren entwickelt (die Grundlagen dazu hatte ich ja in Einstein verstehen Teil II besprochen), dann lässt sich dieser Unterschied direkt nachweisen.
Die Variation der Sonnentageslänge rührt daher, dass sich die Erde auf einer Bahn um die Sonne bewegt, und das im Laufe eines Jahres einmal, nämlich wie folgt:
Von der Erddrehung zum Sonnentag
Fangen wir mit einer stark vereinfachten Situation an, in der Sonne und Erde relativ zueinander ruhen und Erdachse und Verbindungslinie Erde-Sonne senkrecht zueinander stehen. In dieser einfachen Anordnung kommt der Wechsel von Tag und Nacht nur durch die Drehung der Erde zustande. Der Beobachtungsort ist hier durch einen roten, zur Sonne zeigenden Pfeil markiert. Zusätzlicher Einfachheit halber befindet er sich direkt auf dem Äquator:

Immer, wenn der rote Pfeil direkt zum Sonnenball zeigt (das ist in der Grafik alle vier Sekunden der Fall) ist für den entsprechenden Beobachter Mittag, und das mit großer Regelmäßigkeit.
Allerdings bewegt sich die Erde, wie gesagt, um die Sonne. Die folgende Animation folgt einem kurzen Abschnitt des Verlaufs, und hält das Geschehen dabei mehrmals an:
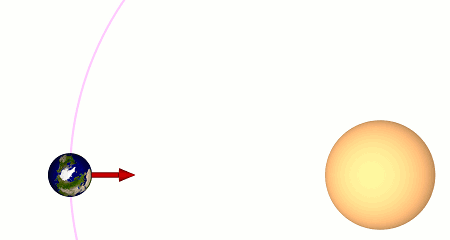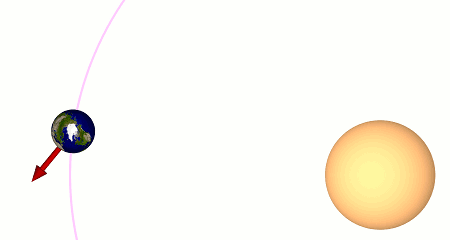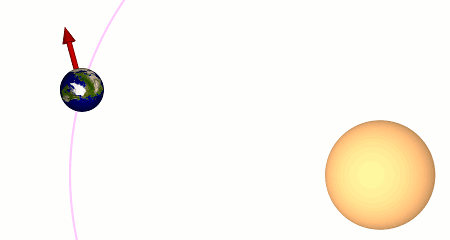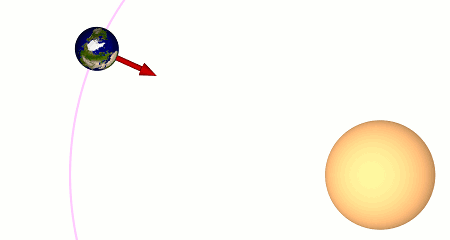
Ganz zu Anfang verharrt die Animation, während für den Beobachter auf der Erde (den roten Pfeil) exakt Mittag ist (der rote Pfeil zeigt direkt auf die Sonne, in diesem Fall: direkt nach rechts). Dann lassen wir die Zeit weiterlaufen: Die Erde dreht sich und bewegt sich dabei zugleich ein wenig weiter auf ihrer Bahn um die Sonne (dem in Magenta eingezeichneten Kreisbogen). Wir halten die Erde an, als sie sich einmal um sich selbst gedreht hat, sprich: als der Pfeil wieder genau nach rechts zeigt. Allerdings zeigt der Pfeil jetzt noch nicht auf die Sonne – obwohl die Erde sich einmal um sich selbst gedreht hat, ist noch kein Mittag. Der Grund ist, dass sich die Erde auf ihrer Bahn ein wenig weiter bewegt hat; die Erde muss sich erst noch ein wenig weiter drehen, bis wieder Mittag ist. Zu diesem Zeitpunkt, dem zweiten Mittag, hält die Animation wieder an.
Der Zeitraum, in dem sich die Erde einmal um sich selbst dreht (hier: vom ersten bis zum zweiten Mal, wo der Pfeil direkt nach rechts zeigt) heißt Sterntag, da man auch sagen kann: Dies ist der Zeitraum, in dem sich die Erde relativ zu den weit entfernten Fixsternen einmal um sich selbst dreht. Der Zeitraum zwischen zwei aufeinanderfolgenden Mittagen (eigentlich, s.o.: Mitternächten) ist dagegen der Sonnentag, auch wahrer Sonnentag genannt, um ihn von dem mittleren Sonnentag, denn wir später noch kennenlernen werden, zu unterscheiden. Wie die obige Animation zeigt, ist er etwas länger als der Sterntag. Und wie die obige Animation ebenfalls zeigt, entsteht er im Zusammenspiel der Rotation der Erde um ihre eigene Achse und dem Umlauf der Erde um die Sonne.
Die Animation ist dabei, klar, weder räumlich noch zeitlich maßstabsgerecht. Das Jahr dauert für dieses fiktive Erd-Sonne-Paar bloße 15 Sonnentage (bzw. 16 Sterntage).
Warum der Sonnentag variiert
Diese Hintergrundinformationen helfen zu verstehen, warum die Dauer des Sonnentags während des Jahres ein wenig schwankt.
In den vereinfachten Animationen stand die Erdachse senkrecht auf der Bahnebene der Erde. In Wirklichkeit ist die Erdachse aber um den Winkel von rund 23,5 Grad gegenüber der Senkrechten geneigt. Salopp gesagt heißt das: Nur ein Teil der Erdbewegung trägt zur Verlängerung der Tageslänge bei; ein anderer Anteil, senkrecht zum ersten, bewirkt, dass die Sonne mit der Zeit höher am Himmel steht (bis zum Höchststand im Sommer) und dann wieder niedriger (bis zum Niedrigststand im Winter). Wie groß der Anteil ist, der zur Verlängerung der Tageslänge beiträgt, variiert dabei im Laufe des Jahres; zur Zeit der Tagundnachtgleiche ist er am geringsten, zur Zeit von Höchst- bzw. Niedrigststand (Sommersonnenwende und Wintersonnenwende) am größten. Dementsprechend variiert die Länge des Sonnentages; zur Zeit der Tagundnachtgleiche ist der Sonnentag am kürzesten, zur Zeit von Sommer- bzw. Wintersonnenwende am längsten.
Hinzu kommt ein weiterer Effekt, nämlich dass die Geschwindigkeit der Erde auf ihrer Umlaufbahn um die Sonne etwas variiert. Die Erde bewegt sich nicht auf einer Kreis-, sondern auf einer Ellipsenbahn, in derem einen Brennpunkt die Sonne steht (1. Kepler’sches Gesetz). Kommt die Erde der Sonne näher – die größte Annäherung findet dabei im Winter statt –, dann läuft sie etwas schneller; in größerer Entfernung von der Sonne läuft sie langsamer (2. Kepler’sches Gesetz oder, in der Sprache der moderneren Physik, Drehimpulserhaltung).
Im Winter etwas schnellerer Bahnlauf, im Sommer etwas langsamerer, das heißt auch: Im Winter etwas längere Sonnentage, im Sommer etwas kürzere.
Auf dieser Seite der Wiener Arbeitsgemeinschaft für Astronomie sind die beiden Effekte schön bebildert. Zusammen ergibt sich über das Jahr hinweg eine Variation, die sich am besten darstellen lässt, wenn man als Bezugsgröße die Länge des mittleren Sonnentags nimmt, sprich: den über das ganze Jahr gebildeten Mittelwert der Längen der unterschiedlichen Sonnentage.
In der folgenden Grafik ist dafür auf der x-Achse die Zeit aufgetragen, gemessen in mittleren Sonnentagen. Auf der y-Achse ist eine Näherungskurve für Abweichung dieser Zeit von der lokalen Zeit (der Zeit seit Jahresanfang, gemessen in tatsächlichen Sonnentagen) aufgetragen, die so genannte Zeitgleichung:
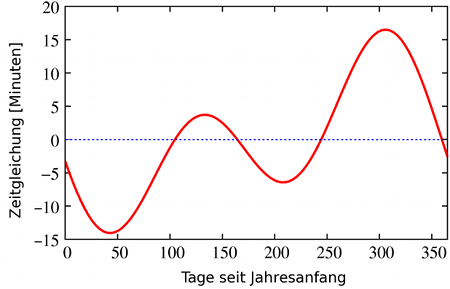
Die dargestellte Abweichung muss man kennen, wenn man anhand der üblichen, mit Hilfe von Uhren gemessenen Zeit den Unterschied zwischen dem auf der Uhr angezeigten Mittag (12 Uhr Winterzeit auf der Uhr) und dem lokalen Mittag (Zeitpunkt des höchsten Sonnenstands) ermitteln will – anders gesagt: den Unterschied zwischen Sonnenuhr und Armbanduhr. Menschen, die sich intensiv mit Bau und Funktionsprinzipien von Sonnenuhren beschäftigen, dürften denn auch diejenigen sein, die sich mit diesem Problemkreis am besten auskennen dürften.
Der mittlere Sonnentag
Im Zusammenhang mit der letzten Grafik hatte ich ihn kurz erwähnt: den mittleren Sonnentag, dessen Länge man erhält, indem man die Längen der wahren Sonnentage über ein Jahr hinweg mittelt. (Muss man sich an dieser Stelle auch über die leicht unterschiedlichen Definitionen des Jahres Gedanken machen? Nein; die sich periodisch ändernde Länge der Sonnentage definiert selbst den genauen Zeitraum, über den wir mitteln müssen.)
Mit dem mittleren Sonnentag war das Ziel erreicht – dachte man zumindest bis in die ersten Dekaden des 20. Jahrhunderts hinein. Hier war eine Tagesdefinition die sich, soweit sich das mit den verfügbaren Uhren nachmessen ließ, nicht mehr mit der Zeit änderte und daher für die Festlegung einer Zeiteinheit taugte.
Mit diesem mittleren Sonnentag und seiner gleichmäßigen Unterteilung in 24 Stunden, jene wiederum in je 60 Minuten unterteilt und jede Minute in 60 Sekunden, gelangen wir zur Sonnensekunde, deren Dauer einem 86.400tel der Dauer des mittleren Sonnentags entspricht (86.400 = 24·60·60).
Und dann beginnen die wirklichen Probleme. Bis hierhin war die Geschichte der stetig verbesserten Sekundendefinition reines astronomisches Grundwissen. Im nachfolgenden Teil II wird es geschichtlicher-vertrackter, bis hin zur modernen Definition der Sekunde mit Hilfe von Atomuhren.
Text und alle Abbildungen, wo nicht anders vermerkt, © 2011 Markus Pössel


Sonnentag
Schöner Artikel, ich kann mir aber nicht verkneifen, auf einen Fehler hinzuweisen. Es muss heißen:
Ein Sonnentag entspricht einem vollständigen Umlauf der Sonne um die Erde.
Im Artikel steht es umgekehrt, das wäre jedoch die Definition eines Jahres.
Bevor jetzt jemand einwendet, die Sonne dreht sich doch gar nicht um die Erde: Doch, tut sie. In einem mit der Erde verbundenen Koordinatensystem, in dem wir uns alle bewegen, dreht sich die Sonne um die Erde.
Antwort von MP: Argh! Irgendein Tippfehler rutscht immer durch. Danke für den Hinweis; habe ich geändert!