Astronomisches Grundwissen 3: Unser Sonnensystem
BLOG: RELATIV EINFACH

Dieser Blogbeitrag ist Teil einer zehnteiligen Serie, die astronomisches Grundwissen vermitteln soll. Alle Beiträge auf einen Blick:
- Nachthimmel, Lichtverschmutzung, Beobachtungen
- Bilder, Spektren, Einfluss der Atmosphäre, Entfernungen
- Unser Sonnensystem
- Die Sonne und andere Sterne
- Das Leben der Sterne
- Exoplaneten
- Die Milchstraße und andere Galaxien
- Kosmische Strahlung, Gravitationslinsen, großräumige Struktur
- Kosmische Expansion und Urknall
- Galaxienentwicklung, Dunkle Energie und Ausblick
Näheres zur Motivation der Serie und dazu, was ich unter astronomischem Grundwissen verstehe, findet sich hier in Teil 1.
Unser Sonnensystem
Unser Sonnensystem ist einfach organisiert: Im Mittelpunkt (zumindest fast!) steht unsere Sonne, ein Stern mit vergleichsweise geringer Masse. Rund um die Sonne kreisen acht Planeten: kugelförmige Gebilde, deutlich kleiner als Sterne. Einer davon ist unsere Erde. Die anderen Planeten können wir je nachdem, wo sie und die Erde sich auf ihren Umlaufbahnen befinden, am Nachthimmel sehen – nicht, weil sie selbst (wie die Sonne) Licht produzieren würden, sondern weil sie das Licht der Sonne reflektieren.
Die Planeten umkreisen die Sonne alle mehr oder weniger in der gleichen Ebene, die Erdbahn- oder Ekliptikebene genannt wird. Einige von ihnen werden ihrerseits von kleineren Himmelskörpern umkreist: ihren Monden. All das gegenseitige Umkreisen wird mit großer Genauigkeit durch das Gravitationsgesetz und die Grundgesetze der Mechanik beschrieben, die Isaac Newton im späten 17. Jahrhundert aufgestellt hat. In guter Näherung folgen die Bahnen der Planeten dabei den von Johannes Kepler im frühen 17. Jahrhundert ausformulierten drei “Keplerschen Gesetzen”. Das erste davon besagt, dass die Planeten auf Ellipsen um die Sonne laufen (also auf “abgeflachten Kreisen”; anstatt wie ein Kreise durch einen festen Radius und einzigen Mittelpunkt werden Ellipsen durch zwei sogenannte Brennpunkte und die konstante Summe der Abstände zu diesen Brennpunkten definiert; in einem der Brennpunkte steht die Sonne). Das zweite besagt, dass sie umso schneller laufen, je näher sie auf ihrer Umlaufbahn der Sonne kommen (der sonnennächste Bahnpunkt heißt “Perihel”, der sonnenfernste “Aphel”). Das dritte hält fest welcher einfache Zusammenhang zwischen der Umlaufzeit eines Planeten und seiner mittleren Entfernung von der Sonne besteht (Umlaufzeit-Quadrat ist proportional zu Entfernung-hoch-drei).
Bereits aus der newtonschen Beschreibung ergeben sich kleinere Abweichungen zu den keplerschen Gesetzen. Ein Planet wird nicht nur von der Sonne, sondern auch von den anderen Körpern im Sonnensystem durch die Schwerkraft angezogen. Bei ganz genauen Messungen ergibt sich noch eine weitere Abweichung: der sonnennächste Bahnpunkt jedes Planeten wandert mit der Zeit minimal weiter, in genau definierter Weise. Darin äußert sich, dass Newtons Gravitationstheorie ihrerseits nur eine Näherung ist. Die genauere Theorie der Gravitation, auch im Sonnensystem, ist Albert Einsteins 1915 aufgestellte Allgemeine Relativitätstheorie.
Weltbilder
Wenn wir noch weiter in die Vergangenheit der Astronomie zurückgehen, stoßen wir auf Konflikte zwischen grundverschiedenen Weltbildern, vor allem dem ptolemäischen Weltbild aus der griechischen Antike, bei dem die Erde im Mittelpunkt des Weltalls stand, und dem kopernikanischen, aufgestellt von Nikolaus Kopernikus im frühen 16. Jahrhundert, mit der Sonne im Mittelpunkt. Wie wichtig die Frage, welcher Körper denn nun im Mittelpunkt steht, damals vornehmlich aus religiösen Gründen genommen wurde, sehen heutige Astronomen mit einigem Befremden. Bekannt ist, dass Galileo Galilei sich durch das Eintreten für das kopernikanische System beachtlichen Ärger mit der römischen Inquisition bekam. Dass er, nachdem er 1633 gezwungen worden war, seinen Überzeugungen öffentlich abzuschwören, trotzig murmelte “Eppur si muove”, also “und sie [die Erde] bewegt sich doch”, dürfte allerdings eine Legende sein. Dass er von der katholischen Kirche immerhin 1992 rehabilitiert wurde, jedoch nicht.
Dass das kopernikanische System zumindest seit seiner Modifizierung durch Kepler eine weit genauere Beschreibung des Sonnensystems liefert, ist unbestreitbar. Die Modelle der Planetenentstehung, die wir später noch kennenlernen werden, haben die zentrale Position der Sonne noch weiter zementiert: Die Sonne befindet sich näherungsweise im Schwerpunkt desjenigen Teils der kollabierenden Gaswolke, aus der Sonne und Planeten entstanden sind; erst im Laufe des Kollapses hat sich die schnell rotierende Scheibe gebildet, aus der dann die Planeten hervorgegangen sind. Unbeweglich ist die Sonne dabei allerdings nicht, sondern sie bewegt sich um den gemeinsamen Schwerpunkt des Systems.
Gekränkt fühlt sich durch unsere Stellung im All heute wohl niemand mehr. Dabei sind wir in einem Weltbild, in dem die Sonne nur ein Stern unter Abermilliarden in einer Galaxie unter Abermilliarden ist, längst noch deutlich weiter an den Rand des Geschehens gerückt als durch die kopernikanische Revolution.
Die Planeten in unserem Sonnensystem
Zur Reihenfolge der Planeten gibt es verschiedene Merksprüche. Der bekannteste dürfte “Mein Vater Erklärt Mir Jeden Sonntag Unseren Nachthimmel” sein – Merkur, Venus, Erde, Mars, Jupiter Saturn, Uranus, Neptun. Die Planeten fallen dabei in zwei Gruppen: die kleineren terrestrischen (alternativ: erdähnlichen oder Gesteins-)Planeten Merkur, Venus, Erde und Mars mit fester Oberfläche und die deutlich größeren Gasplaneten Jupiter, Saturn, Uranus und Neptun. Im Vergleich mit der Sonne sind die Planeten und weiteren kleineren Körper allerdings nur Kleinkram. Knapp 99,9% der Gesamtmasse des Sonnensystems entfallen auf die Sonne!
Kurzsteckbriefe der Planeten:
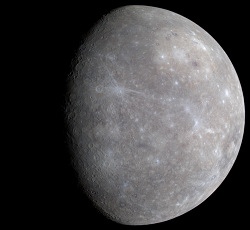 Merkur ist der kleinste und, da der Sonne am nächsten, auch der schnellste der Planeten. Er hat keine nennenswerte Atmosphäre, ähnelt an seiner Oberfläche unserem Mond, und weist beeindruckende Temperaturunterschiede zwischen Tag und Nacht auf. Er besitzt keinen Mond. Merkur hat von uns aus gesehen Phasen wie der Erdmond (Halbmerkur, zunehmender Merkur…). (Rechts ein Merkur-Bild vom Vorbeiflug der Messenger-Raumsonde, NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington.)
Merkur ist der kleinste und, da der Sonne am nächsten, auch der schnellste der Planeten. Er hat keine nennenswerte Atmosphäre, ähnelt an seiner Oberfläche unserem Mond, und weist beeindruckende Temperaturunterschiede zwischen Tag und Nacht auf. Er besitzt keinen Mond. Merkur hat von uns aus gesehen Phasen wie der Erdmond (Halbmerkur, zunehmender Merkur…). (Rechts ein Merkur-Bild vom Vorbeiflug der Messenger-Raumsonde, NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington.)
 Venus ist nur wenig kleiner als die Erde. Aus der Nähe besehen (wie links in einem Bild der NASA-Sonde Mariner 10, bearbeitet von R. Nunes) zeigt sie undurchsichtige Wolken, eine dichte Atmosphäre hauptsächlich aus Kohlendioxid. Aufgrund des Treibhauseffekts hat sie Oberflächentemperaturen von mehr als 460 Grad Celsius (von der Sonne selbst abgesehen ist das der Sonnensystem-Rekord). Von der Erde aus ist Venus als helles Scheibchen (mal als Abendstern, mal als Morgenstern) zu sehen. Sie zeigt von uns aus gesehen Phasen wie der Erdmond (Halbvenus, zunehmende Venus…). Venus besitzt keinen Mond.
Venus ist nur wenig kleiner als die Erde. Aus der Nähe besehen (wie links in einem Bild der NASA-Sonde Mariner 10, bearbeitet von R. Nunes) zeigt sie undurchsichtige Wolken, eine dichte Atmosphäre hauptsächlich aus Kohlendioxid. Aufgrund des Treibhauseffekts hat sie Oberflächentemperaturen von mehr als 460 Grad Celsius (von der Sonne selbst abgesehen ist das der Sonnensystem-Rekord). Von der Erde aus ist Venus als helles Scheibchen (mal als Abendstern, mal als Morgenstern) zu sehen. Sie zeigt von uns aus gesehen Phasen wie der Erdmond (Halbvenus, zunehmende Venus…). Venus besitzt keinen Mond.
 Die Erde hat gerade den richtigen Abstand von der Sonne, dass flüssiges Wasser möglich ist, und liegt damit in der sogenannten habitablen (bewohnbaren) oder lebensfreundlichen Zone unseres Heimatsterns. Bislang ist sie der einzige belebte Himmelskörper im Weltall, den wir kennen. Ihre Oberfläche ist zu rund 70 Prozent von Wasser bedeckt. Sie hat einen Trabanten, den wir mit der uns eigenen Bescheidenheit schlicht “den Mond” nennen. Er ist vermutlich entstanden, als die Erde kurz nach der Entstehung des gesamten Sonnensystems vor rund 4,5 Milliarden Jahren mit einem anderen jungen Planeten zusammenstieß – ein Teil der Kollisionstrümmer bildete den Mond, der Rest wurde Teil der danach deutlich größeren Erde. Rechts ist die berühmte “Blue Marble” zu sehen, die “Blaue Murmel”, die Astronauten von Apollo 17 im Jahr 1972 aufgenommen haben. Eine legendäre Aufnahme, die weite Verbreitung gefunden hat. Wahrscheinlich, weil sie den Menschen erstmals den Umstand direkt vor Augen führte, dass wir alle Bürger ein und desselben Planeten sind – in einem ansonsten ziemlich großen und leeren Weltall. Auch das ist ein sehr wichtiger Teil der astronomischen Allgemeinbildung.
Die Erde hat gerade den richtigen Abstand von der Sonne, dass flüssiges Wasser möglich ist, und liegt damit in der sogenannten habitablen (bewohnbaren) oder lebensfreundlichen Zone unseres Heimatsterns. Bislang ist sie der einzige belebte Himmelskörper im Weltall, den wir kennen. Ihre Oberfläche ist zu rund 70 Prozent von Wasser bedeckt. Sie hat einen Trabanten, den wir mit der uns eigenen Bescheidenheit schlicht “den Mond” nennen. Er ist vermutlich entstanden, als die Erde kurz nach der Entstehung des gesamten Sonnensystems vor rund 4,5 Milliarden Jahren mit einem anderen jungen Planeten zusammenstieß – ein Teil der Kollisionstrümmer bildete den Mond, der Rest wurde Teil der danach deutlich größeren Erde. Rechts ist die berühmte “Blue Marble” zu sehen, die “Blaue Murmel”, die Astronauten von Apollo 17 im Jahr 1972 aufgenommen haben. Eine legendäre Aufnahme, die weite Verbreitung gefunden hat. Wahrscheinlich, weil sie den Menschen erstmals den Umstand direkt vor Augen führte, dass wir alle Bürger ein und desselben Planeten sind – in einem ansonsten ziemlich großen und leeren Weltall. Auch das ist ein sehr wichtiger Teil der astronomischen Allgemeinbildung.
 Mars ist ungefähr halb so groß wie die Erde, besitzt eine viel dünnere Atmosphäre und eine rötliche Oberfläche (Rost!) sowie Polkappen aus Kohlendioxideis. Er dürfte vor Milliarden von Jahren flüssiges Wasser besessen haben und enthält unter der Oberfläche auch heute noch Wassereis. Gibt es dort Leben? Wenn, dann nur primitives, und selbst davon bislang noch keine eindeutigen Spuren. Zukünftige Mars-Missionen werden weiter danach suchen. Mars hat zwei kleine, unförmige Monde. Die Aufnahme links hat das Weltraumteleskop Hubble von seiner Erdumlaufbahn aus gemacht (Bild: ESA/NASA/Hubble Heritage Team (STScI/AURA)).
Mars ist ungefähr halb so groß wie die Erde, besitzt eine viel dünnere Atmosphäre und eine rötliche Oberfläche (Rost!) sowie Polkappen aus Kohlendioxideis. Er dürfte vor Milliarden von Jahren flüssiges Wasser besessen haben und enthält unter der Oberfläche auch heute noch Wassereis. Gibt es dort Leben? Wenn, dann nur primitives, und selbst davon bislang noch keine eindeutigen Spuren. Zukünftige Mars-Missionen werden weiter danach suchen. Mars hat zwei kleine, unförmige Monde. Die Aufnahme links hat das Weltraumteleskop Hubble von seiner Erdumlaufbahn aus gemacht (Bild: ESA/NASA/Hubble Heritage Team (STScI/AURA)).
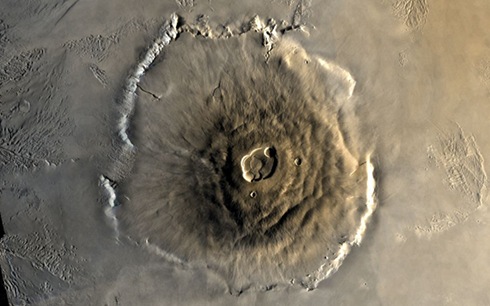
Ach ja: Mit dem Vulkan Olympus Mons (Höhe mehr als 26 Kilometer; Abbruchkanten am Rand so hoch wie der Mount Everest, Grundfläche 80% der Fläche von Deutschland) hat Mars den größten Berg im Sonnensystem (Bild: NASA):
Zwischen den Bahnen von Mars und Jupiter liegt der Asteroidengürtel, in dem unzählige kleinere Felsbrocken die Sonne umlaufen – für rund 400,000 davon sind die Bahndaten im Einzelnen bekannt. Nach heutigem Wissensstand handelt es sich um Brocken aus der Frühzeit des Sonnensystems, die sich aufgrund des störenden Einflusses des Jupiters nicht zu einem weiteren Planeten zusammenfügen konnten. Insgesamt enthält der Asteroidengürtel eine Masse von nur rund 1/2000 der Erdmasse (siehe hier [PDF]).
 Nachweisen kann man Asteroiden, weil sie sich vor dem Hintergrund der Fixsterne bewegen. Das ist in dem Bild rechts sehr schön zu sehen (Aufnahmen: S. Sposetti; Animation: R. Behrend, Observatoire Genève), in dem das Teleskop auf den Asteroiden exakt in der Bildmitte zielt, an dem die Fixsterne scheinbar einträchtig vorbeiziehen. Eine Reihe von Asteroiden laufen auf Bahnen um die Sonne, die sie weit ins innere Planetensystem führen. Einige der sogenannten erdnahen Asteroiden, die auf ihrem Lauf die Erdbahn kreuzen, könnten in Zukunft mit der Erde kollidieren. Solch ein Einschlag kann katastrophale Folgen haben – die Kollision der Erde mit einem Asteroiden oder Kometen vor 65 Millionen Jahren dürfte das Aussterben der Dinosaurier verursacht oder zumindest dazu beigetragen haben (die Details sind Gegenstand aktueller Forschung). Dementsprechend genau bemüht man sich, die Bahnen solcher Objekte zu überwachen.
Nachweisen kann man Asteroiden, weil sie sich vor dem Hintergrund der Fixsterne bewegen. Das ist in dem Bild rechts sehr schön zu sehen (Aufnahmen: S. Sposetti; Animation: R. Behrend, Observatoire Genève), in dem das Teleskop auf den Asteroiden exakt in der Bildmitte zielt, an dem die Fixsterne scheinbar einträchtig vorbeiziehen. Eine Reihe von Asteroiden laufen auf Bahnen um die Sonne, die sie weit ins innere Planetensystem führen. Einige der sogenannten erdnahen Asteroiden, die auf ihrem Lauf die Erdbahn kreuzen, könnten in Zukunft mit der Erde kollidieren. Solch ein Einschlag kann katastrophale Folgen haben – die Kollision der Erde mit einem Asteroiden oder Kometen vor 65 Millionen Jahren dürfte das Aussterben der Dinosaurier verursacht oder zumindest dazu beigetragen haben (die Details sind Gegenstand aktueller Forschung). Dementsprechend genau bemüht man sich, die Bahnen solcher Objekte zu überwachen.
 Jupiter ist der größte Planet im Sonnensystem – sowohl was seine Masse als auch was seinen Durchmesser angeht. Er ist ein Gasplanet: Er besteht überwiegend aus Wasserstoff und Helium. Charakteristisch für die Oberflächenstruktur sind gigantische Wolkenbänder unterschliedlicher (weißlich, bräunlich, rötlich) Färbung parallel zum Äquator. Auffälligste weitere Erscheinung ist der “Große Rote Fleck”, ein gigantischer Wirbelsturm größer als die gesamte Erde, der mindestens solange vor sich hinwirbelt, wie Menschen den Jupiter durch hinreichend große Fernrohre beobachtet haben. Er ist auf dem Bild links (Cassini-Raumsonde, NASA/JPL/University of Arizona) schön zu sehen.
Jupiter ist der größte Planet im Sonnensystem – sowohl was seine Masse als auch was seinen Durchmesser angeht. Er ist ein Gasplanet: Er besteht überwiegend aus Wasserstoff und Helium. Charakteristisch für die Oberflächenstruktur sind gigantische Wolkenbänder unterschliedlicher (weißlich, bräunlich, rötlich) Färbung parallel zum Äquator. Auffälligste weitere Erscheinung ist der “Große Rote Fleck”, ein gigantischer Wirbelsturm größer als die gesamte Erde, der mindestens solange vor sich hinwirbelt, wie Menschen den Jupiter durch hinreichend große Fernrohre beobachtet haben. Er ist auf dem Bild links (Cassini-Raumsonde, NASA/JPL/University of Arizona) schön zu sehen.
Unter all dem Gas enthält der Jupiter vermutlich einen relativ kleinen Gesteinskern, der immer noch deutlich größer als die Erde ist. Jupiter besitzt mehr als 60 Monde; die meisten davon sind sehr klein, und es werden immer wieder neue gefunden. Die vier größten Jupitermonde entdeckte bereits Galileo Galilei bei einigen der ersten astronomischen Teleskop-Beobachtungen überhaupt, darunter Io mit aktivem Vulkanismus und Europa, deren Ozean unter kilometerdicker Eiskruste als möglicher Ort für Leben im Sonnensystem gehandelt wird.
 Saturn ist etwas kleiner als Jupiter, ebenfalls ein Gasplanet mit (weniger deutlich ausgeprägten) Wolkenbändern. Sein auffälligstes Merkmal ist ein System aus mehr als 100.000 ineinandergeschachtelten Ringen, das in groben Zügen bereits mit einem vergleichsweise kleinen Teleskop sichtbar ist (rechts im 50 cm-Teleskop des MPIA und des Hauses der Astronomie, Bild C. Liefke) und Saturn zu einem der reizvollsten Beobachtungsobjekte am Himmel macht. Ob die Ringe zusammen mit Saturn selbst oder aus einem durch Saturns Schwerkraft zerrissenen Mond entstanden sind, ist noch nicht geklärt. Saturn hat ebenfalls mehr als 60 zumeist kleine Monde; einige davon befinden sich im Ringsystem und erzeugen dort z.B. interessante gezwirbelte Strukturen.
Saturn ist etwas kleiner als Jupiter, ebenfalls ein Gasplanet mit (weniger deutlich ausgeprägten) Wolkenbändern. Sein auffälligstes Merkmal ist ein System aus mehr als 100.000 ineinandergeschachtelten Ringen, das in groben Zügen bereits mit einem vergleichsweise kleinen Teleskop sichtbar ist (rechts im 50 cm-Teleskop des MPIA und des Hauses der Astronomie, Bild C. Liefke) und Saturn zu einem der reizvollsten Beobachtungsobjekte am Himmel macht. Ob die Ringe zusammen mit Saturn selbst oder aus einem durch Saturns Schwerkraft zerrissenen Mond entstanden sind, ist noch nicht geklärt. Saturn hat ebenfalls mehr als 60 zumeist kleine Monde; einige davon befinden sich im Ringsystem und erzeugen dort z.B. interessante gezwirbelte Strukturen.
 Der blassbläuliche Uranus ist ebenfalls ein Gasplanet. Unter einer dicken Gasschicht, die einen fast strukturlosen Anblick bietet, verbirgt sich offenbar ein noch dickerer Mantel vorwiegend aus Wassereis; dementsprechend heißen Uranus und der noch weiter entfernte Neptun auch “Eisriesen”. Die Achsen, um die die anderen Planeten des Sonnensystems rotieren, stehen nahezu senkrecht auf der Umlaufebene der Planeten; diejenige des Uranus liegt dagegen in dieser Ebene. In denjenigen Bahnabschnitten, wo seine Achse direkt auf die Sonne zeigt, sieht es daher so aus, als “rolle” Uranus um die Sonne. Uranus besitzt fast 30 Monde. Links ist er in einer Abbildung des Hubble-Weltraumteleskops zu sehen (Bild: NASA/ESA/M. Showalter [SETI Institute]); das Bild des Planeten selbst wurde dabei mit einem Bild der (ungleich leuchtschwächeren, im Infraroten aufgenommenen) Ringe kombiniert.
Der blassbläuliche Uranus ist ebenfalls ein Gasplanet. Unter einer dicken Gasschicht, die einen fast strukturlosen Anblick bietet, verbirgt sich offenbar ein noch dickerer Mantel vorwiegend aus Wassereis; dementsprechend heißen Uranus und der noch weiter entfernte Neptun auch “Eisriesen”. Die Achsen, um die die anderen Planeten des Sonnensystems rotieren, stehen nahezu senkrecht auf der Umlaufebene der Planeten; diejenige des Uranus liegt dagegen in dieser Ebene. In denjenigen Bahnabschnitten, wo seine Achse direkt auf die Sonne zeigt, sieht es daher so aus, als “rolle” Uranus um die Sonne. Uranus besitzt fast 30 Monde. Links ist er in einer Abbildung des Hubble-Weltraumteleskops zu sehen (Bild: NASA/ESA/M. Showalter [SETI Institute]); das Bild des Planeten selbst wurde dabei mit einem Bild der (ungleich leuchtschwächeren, im Infraroten aufgenommenen) Ringe kombiniert.
 Der äußerste Planet des Sonnensystems ist der tiefblaue Neptun. In dem Bild rechts, das 1989 von der Raumsonde Voyager 2 aufgenommen wurde, hat er dem Jupiterfleck einen “Großen Dunklen Fleck” entgegenzusetzen; dieser Fleck existierte freilich nur einige Monate. Historisch ist der Planet interessant, weil seine Existenz Mitte des 19. Jahrhunderts zunächst aus Bahnstörungen des Uranus abgeleitet und Neptun daraufhin tatsächlich an der vorherberechneten Position gefunden wurde. 13 Neptunmonde sind derzeit bekannt.
Der äußerste Planet des Sonnensystems ist der tiefblaue Neptun. In dem Bild rechts, das 1989 von der Raumsonde Voyager 2 aufgenommen wurde, hat er dem Jupiterfleck einen “Großen Dunklen Fleck” entgegenzusetzen; dieser Fleck existierte freilich nur einige Monate. Historisch ist der Planet interessant, weil seine Existenz Mitte des 19. Jahrhunderts zunächst aus Bahnstörungen des Uranus abgeleitet und Neptun daraufhin tatsächlich an der vorherberechneten Position gefunden wurde. 13 Neptunmonde sind derzeit bekannt.
Pluto war bis 2006 der neunte Planet. Nach heutiger Klassifikation ist er ein Zwergplanet. Im Unterschied zu einem Planeten gemäß der 2006 eingeführten Definition befinden sich zuviele andere Objekte in der Umgebung seiner Umlaufbahn; ein Planet hätte hinreichend viel Anziehungskraft, um seine Umlaufbahn von solchen Objekten zu bereinigen. Pluto dürfte aus Gestein und Wassereis bestehen und hat fünf bekannte Monde. Pluto wurde bislang noch nicht von Raumsondern besucht; 2015 soll die “New Horizons”-Mission das ändern.
Die erwähnten Objekte in der Umgebung der Pluto-Umlaufbahn gehören zum sogenannten Kuiper-Gürtel, der insgesamt aus zehntausenden mehr als 100 Kilometer großen Objekten und unzähligen kleinen besteht. Auch diese Objekte dürften bereits im frühen Sonnensystem entstanden zu sein, ohne anschließend in einem Planeten gelandet zu sein. Der Kuiper-Gürtel hat eine geschätzte Gesamtmasse zwischen 4 und 10% der Erdmasse (hier); aufgrund seiner großen Entfernung von der Erde ist er bislang nicht sehr genau erforscht. Außer Pluto gibt es dort mindestens noch drei weitere Zwergplaneten: Haumea (entdeckt erst 2004), Makemake (2005) und Eris (2005). Eris ist sogar noch etwas größer und massereicher als Pluto, und seine Entdeckung war es, die letztlich zur Einführung der neuen Klasse der Zwergplaneten und damit zur “Degradierung” von Pluto führte.
Eingebettet ist das Sonnensystem in eine kugelförmige Region riesiger Ausdehnung – vielleicht bis hinaus zu einem Lichtjahr Entfernung von der Sonne – in der eisige Felsen, schmutzige Riesenschneebälle und ähnliches umlaufen: die Oortsche Wolke. Diese Region ist noch nicht durch direkte Beobachtungen nachgewiesen. Die Gesamtmasse der Oortschen Wolke ist nur sehr ungenau bekannt (vgl. hier), ist aber mit einigen bis einigen Dutzend Erdmassen im Vergleich zur riesigen Ausdehnung der Wolke auf alle Fälle sehr gering.
Die Existenz der Oortschen Wolke wird aus den Eigenschaften der Kometen erschlossen – “schmutzigen Schneebällen” aus Eis, Staub und einigen organischen Verbindungen, von denen einige aus der Oortschen Wolke ins innere Sonnensystem reisen. Sobald Kometen der Sonne hinreichend nahekommen, entsteht unter dem Einfluss der Sonnenstrahlung und der Teilchen, welche die Sonne fortwährend ins All schleudert (“Sonnenwind”), eine Gas- und Staubstruktur um den Kometenkern herum, deren auffälligstes Merkmal ein mehrteiliger Kometenschweif von einigen Dutzend bis einigen Hundert Millionen Kilometern Länge ist. Diese zusätzliche Struktur gibt den Kometen ihr charakteristisches Erscheinungsbild am Himmel. Rechts, auf dem Bild des Kometen Hale-Bopp (aufgenommen von G. Chester, USNO), sind die beiden Schweife schön zu sehen. Der Plasmaschweif, im Bild blau, besteht aus Gas, aus dessen Atomen Elektronen herausgeschlagen sind (ionisiertes Gas) und das vom Teilchenwind der Sonne mitgerissen wird, fast geradewegs von der Sonne weg. Der Staubschweif, im Bild weiß, besteht aus Staubteilchen, die durch das Sonnenlicht etwas vom Kometen weg gedrückt wurden und ihm jetzt auf seiner Bahn nachfolgen.
Zusätzlich zu den hier genannten Objekten enthält das Sonnensystem noch einiges an Kleinzeug – Meteoroide etwa: kleinere Festkörper, von denen gelegentlich einer in der Erdatmosphäre als Meteor (Sternschnuppe) verglüht, wobei, seltener, ein Rest davon als Meteorit auf der Erdoberfläche ankommt. Ansonsten enthält das Sonnensystem noch eine Menge Staub, konzentriert vor allem in der Umlaufebene der Planeten. Unter guten Bedingungen reflektiert dieser Umlaufebenen-Staub das Sonnenlicht und ist vor der Morgen- und nach der Abenddämmerung als sogenanntes Zodiakallicht zu sehen.
Dass die Planeten zwar einen großen Teil des astronomischen Allgemeinwissens ausmachen, in der eigentlichen Forschung aber eher das Arbeitsgebiet von Planetologen und nicht der Astronomen sind und damit eher ein Teilgebiet der Geowissenschaften als der Astronomie – das ist auch Teil der astronomischen Allgemeinbildung.
Weiter geht es mit Teil 4: Die Sonne und andere Sterne
Ich danke Tilmann Althaus, Carolin Liefke und Jakob Staude für hilfreiche Anmerkungen zu diesem Text.


TNOs und KBOs
Die acht größten transneptunischen Objekte:
http://de.wikipedia.org/wiki/Vorlage:TNO8
Die Verteilung der Objekte des Kuipergürtels:
http://commons.wikimedia.org/…elt_75AU_Large.svg
Toll, aber Verallgemeinerung fehlt
Sehr sorgfältig geschriebener Fliesstext – womit ich Text meine, den man ohne viel Nachdenken durchlesen kann und der ohne Ecken und Kanten ist (ist positiv gemeint).
Interssant wären allgemeine Gesetze und Aussage zu Planetensystemen. Etwas was hier nur mit dem Begriff “habitable Zone” angedeutet wird. Zu diesen allgemeinen Phänomenen in Planetensystemen würden beispielsweise Gezeitenphänome gehören, die gebundene Rotation von sonnnenahen Planeten oder planetennahen Monden, die Entstehungsgeschichte von Planetensystemen, die gesetzmässig zu erwartende oder nicht zu erwartende Zusammensetzung von Planeten in Abhängigkeit vom Muttergestirn, dem Abstand des Planeten zum Zentralgestirn, etc., das Magnetfeld von (bestimmten) Planeten, die Atmospären von Planeten etc.
Der Verfasser versucht, dem Leser die allgemeine Relativitätstheorie Einsteins als die “genauere Theorie der Gravitation” nahezubringen. Dabei verfälscht er unter Missachtung des Relativitätsprinzips der Bewegung den Sachverhalt und kommentiert dessen Geschichte im Detail grob widersprüchlich. Im einzelnen:
1. Der Verfasser schreibt: “Unser Sonnensystem ist einfach organisiert. Im Mittelpunkt (zumindest fast!) steht unsere Sonne”.
Dazu folgende Korrekturen:
1.1. Das Sonnensystem ist nicht “einfach” organisiert, sondern genial. Dazu Isaac Newton, Principia 1713, Scholium generale: “Die Hauptplaneten laufen in geschlossenen Bahnen um die Sonnenbahn, in dazu konzentrischen Kreisen, mit der gleichen Bewegungsrichtung und genauestens in derselben Ebene… Das uns sichtbare, höchst erlesene Gefüge von Sonne, Planeten und Kometen konnte allein durch den Ratschluss und unter der Herrschaft eines intelligenten und mächtigen, wahrhaft seienden Wesens entstehen”.
1.2. Die Sonne “steht” nicht, und nicht “im Mittelpunkt” des Systems – auch nicht “fast”: Der Mittelpunkt ist ein Punkt, den ein Objekt entweder einnehmen kann oder nicht, aber niemals “fast”. Das Zentrum der Sonne ist im Übrigen vom Mittelpunkt des Systems, den es umkreist, unstreitig Tausende von Kilometern entfernt!
1.3. Die Sonne “steht” auch nicht, sondern sie bewegt sich. Das lehren Copernicus,
Galilei und Newton. Nur Kepler hielt – fälschlich! – die Sonne für den ruhenden Mittelpunkt der Welt; bis Einstein kam, der (gegen Copernicus, Galilei und Newton) diese falsche Vorstellung Keplers teilte.
2. Der Verfasser schreibt: “In guter Näherung folgen die Bahnen der Planeten den von Johannes Kepler ausformulierten Keplerschen Gesetzen”.
Dazu folgende Korrekturen:
2.1. Weil die Sonne in Wahrheit nicht im Mittelpunkt des Systems steht und nicht ruht, verschiebt sich dieser Bezugspunkt der Planetenbewegungen mit Kepler und Einstein “exzentrisch” aus der Mitte der Umlaufbahnen der Planeten in Richtung der Bahnperipherie. So entstehen, wie Newton im Detail geometrisch beweist, elliptische Bahnformen um die Sonne als den veränderten Bezugspunkt.
2.2. Die elliptischen Bahnformen ergeben sich geometrisch zwangsläufig aus der – falschen – Annahme, dass die Sonne der ruhende Bezugspunkt der Bahnen sei. Das Kepler-Einstein-Modell ist deshalb eine “Näherung” und nicht mehr. Die tatsächlichen Umlaufbahnen um den wahren ruhenden Mittelpunkt des Systems sind konzentrische exakte Kreise (Ellipsen mit Exzentrizität “Null”). Das zeigt insbesondere Isaac Newton in den Principia an vielen Stellen im Detail.
3. Der Verfasser schreibt: “Bereits aus der Newtonschen Beschreibung ergeben sich kleinere Abweichungen zu den Keplerschen Gesetzen”. Alsdann bezeichnet er die Newtonsche Gravitationstheorie als “Näherung” und die Einsteinsche Theorie als “die genauere”.
Dazu folgende Korrekturen:
3.1. Die Newtonsche Beschreibung – Umlaufbahnen als exakte Kreise nicht um die Sonne, sondern um den gemeinschaftlichen Schwerpunkt des Systems – kennt keine “Abweichungen zu den Keplerschen Gesetzen”. Die Wahrheit ist umgekehrt, dass Keplers und Einsteins Bescshreibungen als (unbestrittene!) “Näherungen” von der exakten Realität der kreisförmigen Bahnen um den Schwerpunkt abweichen. Diese Realität beschreibt Newton exakt – und eben nicht als “Näherung”.
3.2. Dass Einsteins Lehre nicht exakt, sondern – im Gegenteil zu derjenigen Newtons – eine bloße “Näherung” ist, kann man in Einsteins eigenen einschlägigen Publikationen von 1915 zur “allgemeinen Relativitätstheorie” wörtlich nachlesen. Es ist eine grobe Verfälschung der Wahrheit, vor diesem Hintergrund Einsteins Theorie im Verhältnis zu derjenigen Newtons als “die genauere” auszugeben.
4. Der Verfasser schreibt: “Wie wichtig die Frage, welcher Körper denn nun im Mittelpunkt steht, damals vornehmlich aus religiösen Gründen genommen wurde, sehen heutige Astronomen mit einigem Befremden”.
Dazu diese Korrektur: Für Copernicus, Galilei und Newton steht überhaupt kein “Körper” im Mittelpunkt, sondern der “gemeinschaftliche Schwerpunkt” des Systems als ein leerer geometrischer Punkt im Raum. Damit kommt diesem “Raum” eine geometrische Realität zu, die z. B. Einstein bekanntlich leugnet – weshalb er (wie Kepler) die materielle Sonne zum ruhenden Mittelpunkt machte. Es geht hier nicht um “religiöse” Gründe”, sondern um die Bewegungslehre. Das Relativitätsprinzip der Bewegung verlangt nach einem wirklich ruhenden Bezugspunkt. Das kann (gegen Kepler und Einstein) nicht die Sonne sein (und auch kein anderer “Körper”, wie Newton beweist)!
5. Der Verfasser behauptet, die katholische Kirche habe den Galilei 1992 rehabi-litiert.
Dazu diese Korrektur: Papst Johannes Paul II. hat 1992 eine Erklärung abgegeben, die zusammengefasst besagt, dass wir alle Irrende seien; dass Galilei irrtümlich einen materiellen Mittelpunkt der Welt angenommen habe (was falsch ist, siehe oben), und dass das alles eh im “Licht” der Einsteinschen Erkenntnisse obsolet geworden sei.
– Das mag als “Rehabilitierung Galileis” ansehen, wer will.
6. Der Verfasser schreibt, Modelle der Planetenentstehung hätten die zentrale Position der Sonne im unbeweglichen Schwerpunkt des Systems “noch weiter zementiert (!)”. Sofort anschließend aber heißt es: “Unbeweglich ist die Sonne dabei allerdings nicht, sondern sie bewegt sich um den gemeinsamen Schwer-punkt des Systems”.
Dazu fragt der Kommentator nur: “Wie denn nun?” – Und er meint, dass es bald fünfhundert Jahre (“näherungsweise”!) nach dem Erscheinen des Buches des Copernicus (1543) ein Skandal eigener Art ist, welchen Eiertanz hier jemand auf- führt, der als “Experte” die Menschen über elementare Daten und Fakten des Sonnensystems belehren will.
Das kann aber auch alles nicht stimmen?
Ich hab mal gehört, Ptolemäus hatte Recht, die anderen haben getrickst.
Wenn niemand wissen kann, wie die Dinge “wirklich” und “in Wahrheit” sind, dann führen sogenannte “Experten” als “Meinungsführer” die Menschen am Gängelband. Dann ist mit der Wahrheit auch die Freiheit dahin. Genau an diesem Punkt befindet sich die moderne “Wissensgesellschaft”, die von Leschs und Pössels autoritativ “informiert” wird, weil niemand mehr die Verpflichtung Ernst nimmt, sich seines eigenen Verstandes zu bedienen. Man sieht, welcher hohe Rang der Überwindung des antiken Skeptizismus vor 2000 Jahren (Jesus von Nazareth), und dann des scholastischen Skeptizismus vor 500 Jahren (Copernicus) zukam: “Was ist Wahrheit?” Wahrheit ist, was wirklich ist! Dass der Mensch kraft seiner Vernunft das Wirkliche und damit die Wahrheit erkennen kann – das ist die Botschaft, die die Macht der Experten und Autoritäten überwindet: Die Wahrheit macht frei! Wer aber weiß, was “Wahrheit” für die moderne Wissenschaft bedeutet – nämlich nichts! – , der sieht: Wir haben es mit einer erneuten Versklavung des Menschen durch Autoritäten zu tun (“Wissen ist Macht”!), die sich auf einen modernen Skeptizismus namens “Lehrfreiheit” berufen, der mit der “Relativierung” allen Wissens einhergeht, die sich als “Aufklärung” tarnt. Dazu gibt es einen bald tausend Jahre alten Spruch des “aufgeklärten” (!) Islam (Ibn Rushd): Wa allahu a’lam. Das heißt: Nur Allah weiß, wie es wirklich ist. Auf ihn berufen sich moderne Liberale. Es lohnt, über die gesellschaftlichen Konsequenzen einer solchen Maxime nachzudenken.
Was Herr Dellian da schreibt, ist eine traurige Mischung aus seinen eigenen Missverständnissen und damit für die Leser dieses Blogs aus meiner Sicht ohne Wert. Ich hatte Herrn Dellian in einem recht anstrengenden E-Mail-Wechsel versucht zu erklären, wo er falsch liegt – leider ohne Erfolg.
Ich will aus dem Text hier nur zwei physikalische Missverständnisse herausgreifen: Herrn Dellians Behauptung dass “Einsteins Lehre” laut Einstein selbst bereits “eine Näherung” sei, beruht darauf, dass Herr Dellian Einsteins Allgemeine Relativitätstheorie im allgemeinen und die spezielle Näherungslösung, die Einstein damals ableitete, fälschlich in einen Topf wirft und daraus die falsche Behauptung ableitet, die Allgemeine Relativitätstheorie als Ganzes sei bereits als Näherung formuliert.
Ein anderes generelles Missverständnis betrifft die Unfähigkeit, überhaupt mit Näherungsaussagen umzugehen. Selbstverständlich kann ein Körper “fast” im Mittelpunkt eines Kreises stehen, dann nämlich, wenn sein Abstand vom Mittelpunkt deutlich kleiner ist als der Radius des Kreises. Selbst im Vergleich zur Merkurbahn mit einer großen Halbachse von 57 Millionen Kilometern macht der maximale Abstand des Sonnenmittelpunkts vom Sonnensystem-Schwerpunkt nur 2,5 Prozent aus, im Vergleich zur Neptunbahn sind es weniger als ein Promille. Im Vergleich mit den Ausmaßen des Sonnensystems als Ganzes steht die Sonne in der Tat in guter Näherung im Mittelpunkt. Und da eine Erklärung, die gleich zu Anfang mit allen Qualifikationen und Komplikationen ins Haus fällt, typischerweise schwer verständlich ist, ist es vollkommen legitim, ein System erst einmal näherungsweise zu beschreiben (Sonne fast in der Mitte) und weitere Details später zu ergänzen (Sonne kreist um gemeinsamen Schwerpunkt des Sonnensystems).
Die allgemeine Relativitätstheorie Einsteins (AR) gründet sich als “Potentialtheorie” – völlig unbestreitbar – auf die Annahme eines im Mittelpunkt stehenden “Zentralkörpers”, das ist im Sonnensystem nach Einstein “die Sonne” – obwohl diese bekanntlich mitnichten im Mittelpunkt steht, und auch keineswegs “steht”, sondern sich bewegt. O-Ton Einstein zur mathematischen Beschreibung des “Gravitationsfeldes” der Sonne in der AR: “Es befinde sich im Anfangspunkt des Koordinatensystems ein Massenpunkt (die Sonne). Das Gravitationsfeld, welches dieser Massenpunkt erzeugt, kann [aus den Gleichungen der AR; ED] durch sukzessive Approximation berechnet werden” (A. Einstein, Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie, Nov. 1915). Jeder Leser kann selbst beurteilen, ob und inwiefern man es hier mit “Näherungen” anstelle exakter Angaben zu tun hat. Dass im Übrigen der Mittelpunkt der Sonne als “Anfangspunkt des Koordinatensystems” gar nicht in Betracht kommt, weil er sich selbst bewegt, sollte man in Kenntnis des Relativitätsprinzips der Bewegung wohl wissen und kann man bei Newton wörtlich nachlesen (Principia, Buch III Prop. XII, Corollar). Ich habe Newtons Principia studiert, aus dem Lateinischen ins Deutsche übersetzt und vor rund 30 Jahren schon als Auswahlausgabe herausgegeben (verlag Felix Meiner Hamburg, Philos. Bibliothek Nr. 394). Das Problem des Herrn Pössel ist, dass er Newtons authentische Lehre erwiesenermaßen nicht kennt und niemals studiert hat (ebenso wie Einstein selbst, der einmal einräumte, Newton nicht gelesen zu haben, weil das ja alles “in den Lehrbüchern steht”). Markus Pössel benutzt nach meiner Erfahrung seine Stellung als “Experte” dazu, die Ideologie des Einsteinschen Relativismus gegen alle vernünftigen Einwendungen zu immunisieren und im Netz zu verbreiten. Die Wahrheit, d. h. die objektive Realität, interessiert ihn so wenig, wie sie Einstein interessierte. Einstein zu Heisenberg (ca. 1926): “Erst die Theorie entscheidet darüber, was man beobachten kann”. oder schärfer formuliert (wohl schon von Hegel): “Wenn die Realität mit meiner Theorie nicht übereinstimmt, umso schlimmer für die Realität”.
…und damit wiederholen wir jetzt hier öffentlich, was wir schon in unserem E-Mail-Wechsel so unfruchtbar durchexerziert hatten. Seufz.
Sie verwechseln die Theorie als Ganzes (allgemeine Relativitätstheorie) mit einer ganz bestimmten Modellsituation (näherungsweises Gravitationsfeld einer Einzelmasse). Die Existenz eines Zentralkörpers nimmt Einstein (per Definition!) in seiner Modellsituation an. Sie liegt aber nicht der Theorie als Ganzes zugrunde. Die Allgemeine Relativitätstheorie kann auch Modellsituationen beschreiben, in denen kein einziger Zentralkörper in Sicht ist.
Salopp gesagt: Newtons Theorie mag den Fall eines Apfels im Gravitationsfeld korrekt beschreiben; es wäre aber falsch zu sagen, Newtons Theorie “gründe sich unbestreitbar auf die Annahme der Existenz eines Apfels”. Genau so eine falsche Aussage tätigen Sie hier aber.
Ihre Anwürfe, mir ginge es nicht um die Wahrheit, sind besonders dreist, weil ich in unserem E-Mail-Wechsel mit durchaus gehörigem Arbeitsaufwand versucht habe, auf Ihre Interpretation von Newtons Theorien einzugehen. Ich hatte ja z.B. gezeigt, dass die konzentrischen Kreisbahnen die tatsächlich beobachtete Planetenbewegung nicht erklären können, hatte dazu extra Beobachtungsdaten herangezogen und Ihnen ein schönes Diagramm gemacht, das zeigt, wie weit die Vorhersagen der konzentrischen Kreisbahnen von den tatsächlichen Beobachtungen abweichen. Diesen Widerspruch zwischen den Daten und Ihrer Lieblingstheorie hatten Sie allerdings ziemlich gekonnt ignoriert.
Ihr Problem scheint zu sein, dass Sie sich in bestimmte Interpretationen verrennen, dabei in Ermangelung tieferen physikalischen Verständnisses sehr elementare Fehler machen, dann aber so auf Ihre Interpretation festgelegt sind, dass Sie nicht mehr aus der selbstgewählten Sackgasse heraus finden. Ihre unsinnige Aussage oben, die Theorie und spezifische Modellanwendung durcheinanderwirft, ist ein recht aussagekräftiges Beispiel dafür.
Markus Pössel schrieb (27. Juni 2017 @ 16:56):
> [Man soll nicht …] die Theorie als Ganzes (allgemeine Relativitätstheorie) mit einer ganz bestimmten Modellsituation […] verwechseln.
So eine bemerkenswerte öffentliche Formulierung!,
auch hinsichtlich der Frage, ob “Theorien als Ganzes” experimentell prüfbar und ggf. falsifizierbar wären, oder (“nur”) bestimmte Modellsituationen.
> Die Allgemeine Relativitätstheorie kann auch Modellsituationen beschreiben […]
Was gehört denn konkret außerdem zur “Allgemeinen Relativitätstheorie als Ganzem” ?
Definitiv mehr als eine einzige Modellsituation. Aber das wussten Sie vermutlich, oder?
Markus Pössel schrieb (27. Juni 2017 @ 19:43):
> Definitiv mehr als eine einzige Modellsituation.
Damit, dass man nicht mal einen ganzen Satz als Reaktion of eine Frage erhält, geschweige denn einen gescheiten, ist zu rechnen.
Zur Ansicht noch einmal meine obige Frage:
Markus Pössel schrieb (27. Juni 2017 @ 16:56):
> […] Die Allgemeine Relativitätstheorie kann auch Modellsituationen beschreiben […]
Was gehört denn konkret außerdem zur “Allgemeinen Relativitätstheorie als Ganzem” ?
Dafür, dass Sie sich in Ihren Kommentaren hier doch recht häufig in kryptischen-kurzen Andeutungen ergehen, reagieren Sie auf eine Kurzantwort, die zum Nachdenken anregen soll ohne alles auszubuchstabieren, überraschend allergisch.
Aber wenn’s der Wahrheitsfindung dient, hier eine ausführliche Erklärung:
Das Satzfragment, an den Sie Ihre Frage anschließen, lautet vollständiger “Allgemeine Relativitätstheorie kann auch Modellsituationen beschreiben, in denen kein einziger Zentralkörper in Sicht ist” und bezog sich auf Herrn Dellians Behauptung, in der ART gebe es immer automatisch einen Zentralkörper, der nur näherungsweise beschrieben werde, nämlich wie in der einzigen Modellsituation in dem von ihm zitierten Einstein-Artikel.
Ihre Frage, was außerdem konkret zur ART gehört, lautet also im Kontext sinngemäß: “Was gehört denn außer der Modellsituation mit einem einzigen, näherungsweise beschriebenen Zentralkörper konkret zur ART”?
Die lange Antwort: Modellsituationen der Kosmologie beispielsweise, mit einem homogenen/isotropen Universum, oder die Näherungsbeschreibungen für ebene Gravitationswellen, oder die diversen weiteren exakten Lösungen, vom Gödel-Universum zu Taub-NUT, außerdem die simulierten Situationen der numerischen Relativitätstheorie und die Modelle des post-Newton’schen Formalismus mit vielen relativ zueinander bewegten “Massenpunkten” und noch vieles mehr.
Oder kurzgefasst, wenn man davon ausgeht, dass der Fragende im Prinzip weiß, was es da alles an schönen weiteren Modellsituationen gibt, und wenn man daher nur kurz darauf hinweisen will, dass es in der zur Nachfrage zitierten Antwort lediglich darum ging, einer unzulässigen Verkürzung der ART auf eine einzige genäherte Modellsituation entgegenzutreten, eben: “Definitiv mehr als eine einzige Modellsituation”.
Markus Pössel schrieb (27. Juni 2017 @ 20:41):
> […] hier eine ausführliche Erklärung:
Danke für die Ausführlichkeit, anhand der wenigestens der Umfang des Missverständnisses offenbar wird.
> Das Satzfragment, an den Sie Ihre Frage anschließen, lautet vollständiger „Allgemeine Relativitätstheorie kann auch Modellsituationen beschreiben, in denen kein einziger Zentralkörper in Sicht ist“ […]
Offensichtlich. Und davon hatte ich im Kontext meiner obigen Frage bis zum Komma zitiert; einschließlich des Wortes “Modellsituationen“, wohlgemerkt im Plural.
Nämlich um im Kontext meiner Frage zu bekunden, dass ich mich durchaus darauf einlasse zu sagen “eine sogenannte Theorie als Ganzes beschreibt bzw. enthält Modellsituationen”;
und demnach natürlich, ganz selbstverständlich alle Modellsituationen (die sich in den Wertebereichen der in Betracht stehenden Größen, wie u.a. “Bahn” und “Masse” und sicherlich einige mehr, ausdrücken lassen mögen).
> Ihre Frage, was außerdem konkret zur ART gehört, lautet also im Kontext sinngemäß: „Was gehört denn außer der Modellsituation mit einem einzigen, näherungsweise beschriebenen Zentralkörper konkret zur ART“?
Das ist eine erhebliche Fehlinterpretation von Sinn und Kontext meiner obigen Frage.
Auf deren Kontext hatte ich ja, wie ich es gewohnt bin, versucht ganz ausdrücklich hinzuweisen:
ob „Theorien als Ganzes“ experimentell prüfbar und ggf. falsifizierbar wären, oder („nur“) bestimmte “Modellsituationen“.
Ich stelle also meine Frage ein weiteres Mal, erneut unter sorgfälter Verwendung der (27. Juni 2017 @ 16:56) zur Verfügung gestellten zitierten Begriffe, aber nun noch etwas ausführlicher und suggestiver:
Davon ausgehend, dass in der sogenannten „Allgemeinen Relativitätstheorie als Ganzem“ alle “Modellsituationen” enthalten sind, die sich unter Benutzung bestimmter Begriffe bzw. darauf basierender Werte ausdrücken lassen,
enthält sie auch die Definitionen dieser Begriffe als Messgrößen —
Ja oder Nein ?
.
(Vermutlich fällt es nicht schwer, die Antwort auf diese Frage zu finden;
aber ich fände es wertvoll, wenn Kenntnisnahme, Verständnis und Beantwortung dieser Frage öffentlich und Barriere-frei kommentierbar dokumentiert wäre.)
Eine große Bitte: könnten Sie in Zukunft bitte gleich von Anfang an Ihre Fragen in Ihren eigenen Worten mit Nennung des von Ihnen gewünschten Kontextes formulieren? Spart uns dann hoffentlich beiden Zeit und Frust.
Zitate bringen immer ihren eigenen Kontext mit; selbst wenn aus dem Zitat nur Teile wiederholt werden, ist der Kontext immer dabei. Wenn Sie einen anderen Kontext intendieren, weisen Sie doch bitte direkt darauf hin und lassen das Zitat vielleicht besser ganz weg. Sonst sind Missverständnisse relativ verlässlich vorprogrammiert.
Zu Ihrer Frage: Definitionen dieser Begriffe als Messgrößen ja, aber nicht in jedem Falle als beobachterunabhängige Messgrößen, und in der Regel als idealisierte Messgrößen (z.B. mit infinitesimalen Größen oder über Testteilchen), die vor Durchführung einer wirklichen Messung erst noch in eine Praxissituation übersetzt werden müssen. (Beispiel: Testteilchen sind idealisiert definiert; bei der Modellierung in einer tatsächlichen Situation wird dann [begründet!] entschieden, bestimmte reale Objekte als Testteilchen zu modellieren.)
Markus Pössel schrieb (28. Juni 2017 @ 08:10):
> […] Definitionen dieser Begriffe als Messgrößen ja […]
… sind in einer “Theorie als Ganzem” enthalten.
Gut, danke.
Zur Unterscheidung von “Theorie als Ganzem“, die auch alle Modellsituationen (im Rahmen der Wertebereiche der definierten Messgrößen) beinhalten soll,
bietet sich vielleicht der Begriff “Theorie an sich” an, mit dem (lediglich) die axiomatischen Begriffe, daraus konstruierten Definitionen (insbesondere von Messgrößen) sowie alle daraus folgenden Theoreme zusammengefasst sein sollen.
Und wer nun die Meinung verträte: …
… meint damit vermutlich nicht
– dass sich durch Anwendung genau dieser Definitionen zur Bewertung experimenteller Daten zeigen könnte, dass eine, manche oder alle dieser Definitionen falsch wären; oder
– dass sich Zusammenhänge zwischen so gewonnenen Messwerten, die sich aus den Definitionen der Messgrößen als Theoreme herleiten lassen, als falsch erweisen könnten; oder
– dass die selbstverständlichen, allgemeinverständlichen, durchaus praktischen Begriffe, unter deren Benutzung die Definitionen überhaupt erst aufgestellt und formuliert wurden (z.B. Begriffe wie “Koinzidenz” und “Identifizierbarkeit (von Beteiligten)“) von vornherein falsch wären.
Ist vielleicht doch nur gemeint, dass wir mit unseren Experimenten möglichst umfassend versuchen könnten, bestimmte Modellsituationen zu falsifizieren, also zu zeigen, dass die experimentellen Befunde nicht den in der fraglichen Modellsituation beschriebenen Erwartungswerten gleichen ?
Wobei die zur Gewinnung der Messwerte eingesetzte “Theorie an sich” nach wie vor bestehen bleibt und benutzt werden kann, um Messwerte zu gewinnen bzw. um alle einzelnen Modellsituationen zu beschreiben, die in der “Theorie als Ganzem” enthalten sind.
> […] aber nicht in jedem Falle als beobachterunabhängige Messgrößen,
An dieser Stelle wären Beispiele für “beobachterunabhängige Messgrößen” bzw. “beobachterabhängige Messgrößen” aufschlussreich.
(Jede Beurteilung z.B., ob ein bestimmter Beteiligter bestimmte unterscheidbare Wahrnehmungen in Koinzidenz gemacht hat, oder nicht, soll doch gewiss so erfolgen, dass vor allem dieser Beteiligte selbst zum Urteil gelangen würde, sofern er die notwendige beobachterische Urteilsfähigkeit besäße. Und andererseits soll natürlich allen gleichermaßen ganz unmissverständlich mitteilbar sein, welche Messoperationen angewandt und welche Messwerte dadurch erhalten wurden.)
> und in der Regel als idealisierte Messgrößen […], die vor Durchführung einer wirklichen Messung erst noch in eine Praxissituation übersetzt werden müssen.
> Beispiel: Testteilchen sind idealisiert definiert
An diesem Beispiel lassen sich zwei unterscheidbare Arten des “Übersetzens in eine Praxissituation” diskutieren:
(1)
Versuchsanordnungen nicht von bestimmten “besonderen, idealen” (Mess- bzw. Vorgabe-)Werten abhängig zu machen.
Hier also z.B. nicht darauf zu bestehen, dass sich in einem bestimmten Versuch ein “Testteilchen” finden ließe (d.h. dessen Beschleunigungsbetrag durchwegs Null wäre) und den Versuch ansonsten zu verwerfen;
sondern die Beschleunigsbeträge der vorhandenen Teilchen jedenfalls zu messen, und damit zu quantifizieren, welche davon im betreffenden Versuch dem Ideal “Testteilchen” näher kamen als welche anderen.
(2)
Nicht den wahren Wert einer Messgröße in einem bestimmten Versuch durch Anwendung der definierten Messoperation auf die gegebenen Daten zu ermitteln,
sondern durch Anwendung anderer, eventuell “einfacherer, ökonomischerer” Operationen abzuschätzen, und unter Bezug auf die zugrundegelegte (“ideale“) Definition der Messgröße dazu bestimmte Vertrauensbereiche anzugeben.
Zur “Theorie an sich” gehört wohl weder das eine, noch das andere …
p.s.
> Eine große Bitte: könnten Sie in Zukunft bitte gleich von Anfang an Ihre Fragen in Ihren eigenen Worten mit Nennung des von Ihnen gewünschten Kontextes formulieren?
Sich solche Freiheiten zu nehmen, sofern sie überhaupt angebracht wären, setzt das Selbstbewusstsein eines SciLoggers oder zumindest SciLog-Gastautors voraus.
Ich Kommentator dagegen, bei allem Bemühen von Anfang an hier (27. Juni 2017 @ 19:41) und im Allgemeinen, bin heilfroh, wenn meine Fragen trotz der Einschätzung als “häufig kryptisch-kurz” zumindest öffentlich auffindbar bleiben; anstatt als “zu kryptisch” oder “overly speculative”, “too broad”, “off-topic” o. Ä. von vornherein disqualifiziert zu werden.
Zur Frage der Falsifizierung von Theorien: Da war in dem von Ihnen zitierten Beitrag tatsächlich gemeint, dass man möglichst viele, und den erwarteten Geltungsbereich möglichst gut ausschöpfende, Modelle entsprechend auf Diskrepanzen zur Beobachtung testet. War in dem entsprechenden Blogtext azcg im Abschnitt “Überprüfung, Experimente und noch einmal Modelle” etwas näher ausgeführt.
Bei beobachterabhängigen und -unabhängigen Größen hatte ich vor allem wieder Koordinaten im Sinn. Bei der Formulierung von prüfbaren Vorhersagen werden ja in der Regel Koordinaten bemüht (z.B. zur Beschreibung der Planeten im Sonnensystem). Führt ein anderer Beobachter andere Koordinaten ein, muss eben vernünftig transformiert werden – während es bei koordinatenunabhängig definierten Messungen (z.B. Bogenlänge einer gegebenen Kurve zwischen zwei identifizierbaren Ereignissen) direkte Übereinstimmung geben muss.
Zu den “Feinheiten” und dem, was Ihnen als Kommentator möglich oder nicht möglich ist: Ich bezog mich direkt auf die direkte Formulierung, die Sie dann nach einigem Hin- und Her gewählt hatten. Die große Bitte lautete im wesentlichen: bitte gleich so.
Markus Pössel schrieb (28. Juni 2017 @ 16:08):
> Zur Frage der Falsifizierung von Theorien: […]
> dass man […] Modelle entsprechend auf Diskrepanzen zur Beobachtung testet.
Darf davon ausgegangen werden, dass mit “Diskrepanzen zur Beobachtung” dabei gemeint ist, dass Messwerte (der in der Theorie definierten Messgrößen), aus bestimmten Versuchen, ungleich den Erwartungswerten sind, die von einigen bestimmten Modellen zusammengefasst sind ?
Selbstverständlich enthält jede sogenannte “Theorie als Ganzes“, die auch alle Modelle enthalten soll, die sich anhand der Wertebereiche ihrer Messgröen ausdrücken lassen, sowohl (viele) Modelle mit Diskrepanzen zu den ermittelten Messwerten, als auch (etliche) Modelle, die damit übereinstimmen.
Wenn man deswegen sagen sollte “Die Theorie ist falsch bzw. falsifiziert.”,
dann bestünde Anlass dazu, sobald auch nur der erste Messwert ermittelt wurde …
(Dabei verbleiben doch die Definitionen der Messgrößen, also die “Theorie an sich”, genau so nachvollziehbar und anwendbar wie zuvor; sie hätten sich sogar hinsichtlich ihrer Anwendung bewährt, nämlich überhaupt mindestens einen konkreten Messwert zu gewinnen. Und außerdem etliche, auf diesen Definitionen basierende Modelle, deren Erwartungswerte keine Diskrepanz zu den vorhandenen Messwerten aufweisen.)
> in dem von Ihnen zitierten Beitrag […]
Dort war die Korrespondenz leider zum Erliegen gekommen.
Hinsichtlich der in jenem Beitrag angeführten “Konsequenzen […], die sich aus der Theorie erschließen lassen” sei (nochmals) darauf hingewiesen,
dass die Theoreme, die sich (insbesondere) aus den Definitionen der Messgrößen herleiten lassen, doch ganz zwangsläufig als Beziehungen zwischen den entsprechend ermittelten Messwerten repräsentiert sind.
(Sofern natürlich überhaupt Messwerte aus Versuch für Versuch gegebenen Beobachtungsdaten zu ermitteln waren; was vermutlich unter “Geltungsbereich” bzw. “Gültigkeitsgrenzen” verstanden werden soll.)
Das vorgeschlagene “überprüfen, ob sich diese Konsequenzen auch in der Wikrlichkeit zeigen ” läuft folglich schlicht darauf hinaus zu sichten, ob überhaupt relevante Messwerte gefunden würden, indem die definierten Messoperatoren auf gegebene Beobachtungsdaten angewandt werden.
(In dieser Hinsicht, nennen wir’s “Relevanz”, können sich verschiedene Theorien natürlich unterschiedlich “in der Wirklichkeit” bewähren.)
Noch eine Illustration:
> Wenn man feststellt, dass Steine, Eisenkugeln, Holzscheite und eine unübersehbare Vielfalt weiterer Körper, so man sie vom Erdboden abhebt und dann loslässt, zu Boden fallen, dann ist das zu-Boden-fallen offenbar eine allgemeine Eigenschaft.
Wenn der Begriff “zu-Boden-fallen” als Messgröße definiert ist (schlicht mit Booleschem Wertebereich: “Ja” oder “Nein”), dann beinhaltet die entsprechende “Theorie als Ganzes” offenbar nicht nur das Modell, “dass alles immer zu Boden fällt”, sondern auch jede Menge Modelle “dass manches manchmal nicht”. (In den letzteren Fällen spricht man vom jeweiligen “Boden” z.B. auch als “Startbahn” oder “Meeresgrund” oder “unterm Tisch”.)
Um in mehreren Versuchen eventuell eine gleichbleibende “allgemeine Eigenschaft” diagnostizieren zu können, muss man zuerst eine nachvollziehbare Messgröße definiert haben, deren Messwert Versuch für Versuch kommensurabel (reell bzw. Boolean) sind; und daran festhalten.
Ggf. kommt man durch fortgesetzt gleichbleibende Messwerte ja auf den Gedanken, nachgeordnete Messgrößen zu definieren und auszuwerten; z.B. “Stabilität (von Tischen)”, oder “Auftrieb (von Flug- bzw. Schwimmkörpern)”.
p.s.
> […] bei koordinatenunabhängig definierten Messungen (z.B. Bogenlänge einer gegebenen Kurve zwischen zwei identifizierbaren Ereignissen)
Naja: ein echter reell-wertiger Messwert wäre jedenfalls das Verhältnis der “Bogenlänge einer gegebenen Kurve (zwischen zwei identifizierbaren Ereignissen)” und der “Bogenlänge einer geeigneten gegebenen Kurve“.
Aber ich stimme zu: für die Ermittlung eines solchen Wertes spielt es keine Rolle, ob oder wie die dabei in Betracht stehenden Ereignisse mit Koordinaten bestreußelt würden.
> Bei der Formulierung von prüfbaren Vorhersagen werden ja in der Regel Koordinaten bemüht
???
Zur Formulierung der Vorhersage “A trifft B” offenbar nicht.
Zur Formulierung der Vorhersage “M nimmt <dieses> und <jenes> in Koinzidenz wahr” offenbar auch nicht.
Und zur Formulierung von Vorhersagen, die z.B. Verhältnisse von Bogenlängen betreffen, bemüht man Koordinatenwerte wohl nur insofern als diese den betrachteten Ereignissen nicht völlig beliebig zugeordnet würden, sondern, insbesondere, in bestimmtem definierten Zusammenhang zu gemessenen Werten von Bogenlängen-Verhältnissen.
(Womit ich keinesfalls dem seit bald einem Jahr in Aussicht stehenden “gesonderten Blogbeitrag zur Frage von Koordinaten und koordinatenfreien Darstellungen“ vorgreifen möchte … Aber zumindest anmerken, dass die dabei auftretenden Formeln übersichtlich durch \(\LaTeX\)-Befehle darstellbar wären.)
Wie man die Diskrepanzen zur Beobachtung definiert, kann von Fall zu Fall etwas variieren. In moderner Form würde man vermutlich Bayesianisch vorgehen, seinem physikalischen Modell noch Modelle für den Messprozess (z.B.: Gauß’scher Fehler, siehe Teil 3 des entsprechenden Blogeintrags zu Modellen, Theorien, Experimenten) hinzufügen und dann einen Modellvergleich mit der Formel von Bayes machen.
Dass zur Falsifikation nicht ein einziger Messwert genügt, liegt daran, dass in der Schlusskette auch die Modelle, sowohl für die zu beschreibende Situation als auch für die Messung, eine Rolle spielen. Auch wenn der Paradigmenwechsel als Begriff inzwischen ja eher abgegriffen ist: Die Grundbeobachtung, dass die Wissenschaft in dieser Hinsicht eine gewisse Trägheit besitzt und die Falsifikation erst bei einer gewissen Anhäufung von der Theorie widersprechenden Ergebnissen auch auf die Theorie zurückfällt ist ja zutreffend.
Zu-Boden-fallen: Nein, in meinem Beispiel beinhaltet die Theorie (primitiv wie sie ist) nicht das nach-oben-steigen, sondern nur das zu-Boden-fallen. Dass bestimmte Objekte (z.B. Flugzeuge, Papier im Wind etc.) sich anders verhalten ist damit eine Herausforderung für die Theorie. Man kann das entweder durch eine Einschränkung des Gültigkeitsbereichs lösen (oberhalb der Erdoberfläche in der Luft, Objekte ohne Antrieb in bestimmtem Dichtebereich) oder, wie es historisch ja wohl war, die Theorie erweitern und zur Gravitation noch Auftriebskräfte hinzunehmen. Unverändert festhalten sollte man an der Theorie nicht.
Koordinaten und Koinzidenzen: Ich dachte da vor allem an das Sonnensystem. Um das Modell sinnvoll aus der Theorie abzuleiten, sei es Newtonsche oder Einsteinsche Theorie, sind Koordinaten unumgänglich, und auch das entsprechende Modell ist in Form von Koordinaten formuliert. Dann kommen noch Modelle für den Messvorgang hinzu, wo ja z.B. das Konzept einer Uhr wichtig wird, und ganz am Ende bei den Vorhersagen wird es in der Tat auf Koinzidenzen hinauslaufen (z.B. Licht, das vom Teleskop zu einem bestimmten Zeitpunkt, ermittelt als Koinzidenz mit einem bestimmten Zählerstand der Uhr, wieder einkommt). Das Modell wird dadurch aber nicht auf Koinzidenzen reduziert – man kann es nicht aus der Theorie ableiten und nicht mit dem Mess-Modell verbinden, ohne zwischendurch über etwas anderes als Koinzidenzen zu reden.
Markus Pössel schrieb (1. Juli 2017 @ 10:02):
> Zu-Boden-fallen: Nein, in meinem Beispiel beinhaltet die Theorie (primitiv wie sie ist) nicht das nach-oben-steigen, sondern nur das zu-Boden-fallen.
Allein schon diese Bemerkung offenbart: anhaltenden Klärungsbedarf. …
Wie weiter?? …
In dem gerade verlinkten “Teil 3” (an den sich auch schon einige Kommentare anschlossen) finde ich eine relevante Formulierung, der ich (so gut wie) voll und ganz zustimme (sofern ich sie recht verstehe), und die ich deshalb zum Ausgangspunkt für die nochmalige Darlegung meines Einwandes nehmen möchte:
(Allerdings habe ich solche Angaben “wie” in meinen Kommentaren bisher nicht “Rezepte” genannt, sondern “Definitionen von Messgrößen” bzw. “Theorie an sich”, oder gelegentlich auch “Messoperatoren”.)
Dem besagten Beispiel (“Zu-Boden-Fallen“) muss also ein (Versuch für Versuch nachvollziehbares) “Rezept” zugrundeliegen,
durch dessen Anwendung auf die Versuch für Versuch vorgefundenen/gegebenen/gesammelten Daten sich feststellen lassen soll, ob (oder nicht).
Richtig?
Und dieses “Rezept” gilt es zu unterscheiden (d.h. gedanklich zu trennen) von allen Versuchsergebnissen die durch Anwendung des “Rezepts” schon erhalten wurden bzw. in weiteren noch denkbaren Versuchen erhalten werden könnente.
Das “Rezept an sich”, zur Ermittlung des Ergebnisses aus jeweils einem Versuch (gleichermaßen, nachvollziehbar in jedem Versuch),
ist also jedenfalls nicht das Selbe wie das konkrete Ergebnis jeweils eines einzelnen Versuchs,
oder wie irgend eine bestimmte Menge von konkreten Versuchsergebnissen bzw. Erwartungen von Versuchsergebnissen (“ein bestimmtes Modell”).
Und wenn wir schon sagen, dass “das Rezept bestimmte Versuchsergebnsse enthält”, nämlich in dem Sinne, dass ein bestimmter Wertebereich von Versuchsergebnissen durch die (bloße) Definition des “Rezepts” festgesetzt ist,
dann meint das selbstverständlich den gesamten Wertebereich denkbarer Versuchsergebnsse;
d.h. im Bespiel sowohl das “Nach-oben-Steigen“, als auch das “Zu-Boden-Fallen“.
Mit jedem weiteren Versuch stellt sich ehrlicher Weise die Frage erneut:
werden wir (in Anwendung “des Rezepts” auf Beobachtungs-Daten) den einen Ergebniswert erhalten, oder den anderen?.
Auch falls in allen bisherigen Versuchen stets nur der eine Ergebniswert erhalten wurde (z.B. immer “fiel zu Boden”), und falls (deshalb) auch erwartet würde, dass in allen weiteren Versuchen weiterhin stets nur dieser selbe Ergebniswert erhalten wird,
dann stellt sich diese Frage trotzdem stets erneut:
werden wir (in Anwendung “des Rezepts” auf Beobachtungs-Daten) “weiterhin” den einen Ergebniswert erhalten, oder “diesmal” den anderen?.
Die Antwort auf diese Frage lässt sich grundsätzlich nicht aus dem “Rezept an sich” schließen
(sondern nur durch dessen Anwendung auf die Beobachtungs-Daten des betreffenden Versuchs).
Stimmt’s?
> dass die Wissenschaft in dieser Hinsicht eine gewisse Trägheit besitzt und die Falsifikation erst bei einer gewissen Anhäufung von der Theorie widersprechenden Ergebnissen auch auf die Theorie zurückfällt ist ja zutreffend.
Nein:
die Idee von “der Theorie widersprechenden Ergebnissen” ist grundsätzlich absurd; so etwas gibt es gar nicht.
Von Ergebnissen, die (“gerade erst”) durch Anwendung des jeweiligen “Rezepts” erhalten wurden, kann man grundsätzlich nicht behaupten, dass sie (genau diesem) “Rezept” widersprächen.
Bestimmte “Rezepte” (Theorien) fallen nicht etwa wegen der Ergebnisse aus der Mode, die man damit erhalten hat oder noch zu erhalten erwartet,
sondern weil und sofern man durch Anwendung anderer “Rezepte” (Theorien) zusätzliche, möglicher Weise relevantere Ergebnisse erhalten kann.
p.s.
> Koordinaten und Koinzidenzen: […]
Den dazu hier vorgelegten Ausführungen möchte ich ganz entschieden widersprechen; aber dafür besteht wohl die bessere Gelegenheit im Anschluss an den in Aussicht stehenden “<emgesonderten Blogbetrag” zu diesem Thema.
Irgendwie geht’s da durcheinander. Das Rezept der Zuordnung von Messdaten und Theorie-Vorhersagen ist etwas anderes als die Theorie selbst.
Klassische Gravitationstheorie (Newtons Anziehungsgesetz und Gesetze der Mechanik) sagt mir, dass ein hinreichend dichter, elektrisch ungeladener, hinreichend kompakter, nicht mit Antrieb versehener Körper, den ich direkt über der Erdoberfläche loslasse, nach unten fällt. Sie umfasst definitiv nicht die gegenteilige Vorhersage.
Um die Vorhersage zu prüfen, brauche ich das genannte Rezept, z.B.: Ich messe Abstände über dem Erdboden mithilfe eines unter dem Körper auf dem Erdboden angebrachten Ultraschall-Entfernungsmessers. Dieses Rezept lässt in der Tat auch die Möglichkeit zu, dass die Körper ihren Abstand vom Erdboden spontan vergrößern. Der Gravitationstheorie widerspricht ein solcher Ausgang des Experiments aber – und ich müsste dann sehen, ob ich evt. andere Einflüsse übersehen habe oder ob meine Theorie schlicht falsch ist.
Insofern: Klar gibt es einer Theorie widersprechende Ergebnisse. Und die spielen dabei, ob Theorien ins Hintertreffen geraten, eine wichtige Rolle.
Markus Pössel schrieb (2. Juli 2017 @ 18:23):
> Klassische Gravitationstheorie (Newtons Anziehungsgesetz und Gesetze der Mechanik) sagt mir, dass ein hinreichend dichter, elektrisch ungeladener, hinreichend kompakter, nicht mit Antrieb versehener Körper, den ich direkt über der Erdoberfläche loslasse, nach unten fällt.
Ganz recht. Dieses Theorem ergibt sich aus dem Zusammenhang der Einzelheiten der “Rezepte“, die all die genannten Begriffe (“nicht mit Antrieb versehen“, “über der Oberfläche eines Körpers von wesentlich größerer Masse”, “loslassen“, “nach unten bewegen”) als Messgrößen definieren.
Wenn (falls, sofern) die genannten Bedingungen in einem bestimmten Versuch erfüllt gefunden wurden,
dann, zwangsläufig … (um’s besonders ausführlich zu formulieren): sind die dafür ausgewerteten Beobachtungsdaten auch ein Eigenzustand des “Rezepts” zur Feststellung, welche Konsequenz eingetreten ist; mit der genannten Konsequenz als Eigenwert bzw. Messwert im betreffenden Versuch.
Aber:
Klassische Gravitationstheorie (Newtons Anziehungsgesetz und Gesetze der Mechanik) sagt doch ganz gewiss nicht, dass alle der genannten Bedingungen, oder auch nur irgendeine, in einem bestimmten Versuch erfüllt gewesen wären:
– es ist nicht “gesagt”, dass in allen Versuchen alle Körper, die jemand aufheben könnte, sich jedenfalls als “nicht mit Antrieb versehen” herausstellen müssten;
– es ist nicht “gesagt”, dass in allen Versuchen alle Körper, die jemand aufheben könnte und anschließend “loslassen” wollte, auch tatsächlich “loslassen” würden;
– es ist nicht “gesagt”, dass ein bestimmtes “System” von identifizierten Beteiligten in jedem Versuch “geschlossen” bliebe.
Dies sind (ggf., “nur”) Modell-Annahmen bzw. -Vorhersagen;
und die zugrundegelegte Theorie (“an sich”) stellt lediglich die “Rezepte” bereit, um Versuch für Versuch herauszufinden, ob sie erfüllt waren, oder in wie fern nicht.
Man beachte:
Die Modell-Annahmen lassen sich ggf. zu Anforderungen der Versuchsanordnung erklären.
Falls man also (durch Einsatz der festgesetzten “Rezepte“/Theorie) feststellt, dass irgendwelche in der Versuchsanordnung geforderten Bedingungen in einem bestimmten Versuch nicht erfüllt gewesen wären, dann schließt man immer (!), dass der betreffende Versuch ungült war
(und falls jemand dafür unbedingt “Gründe” benannt haben möchte, dann meinetwegen: “wegen Einflüssen“);
und niemals, dass “die Rezepte/Theorie falsch” wäre(n).
> [Das] Rezept lässt in der Tat auch die Möglichkeit zu, dass die Körper ihren Abstand vom Erdboden spontan vergrößern.
Eben.
> Der Gravitationstheorie widerspricht ein solcher Ausgang des Experiments aber
Ganz und gar nicht:
Die Existenz von (aufhebbaren, und loslassbaren) Vögeln ist bestens verträglich mit der Gravitationstheorie;
lediglich nicht mit bestimmten Modellen (die z.B. auch im Tapferen Schneiderlein getestet und für falsch befunden wurden).
Insbesondere ist und bleibt das “Rezept” zur Beurteilung, ob sich ein in Betracht stehender Beteiligter/Körper “nach unten bewegte, oder nicht”, jedenfalls ein wesentlicher Bestandteil der/jeder Gravitationstheorie.
> Irgendwie geht’s da durcheinander. […]
Wir bohren wohl besonders dicke Bretter. …
Ich habe mich hier nicht zu Wort gemeldet, um eine sinnlose Diskussion mit einem
100% Einstein-Gläubigen öffentlich fortzusetzen. Ich will hier auch niemanden belehren. Ich will lediglich die Besucher dieses Blogs warnen, die guten Glaubens darauf vertrauen, sie würden hier mit “astronomischen Grundwissen” versorgt: Beachten Sie, dass dieser Blog vom Vertreter einer Ideologie gelenkt wird, deren Anliegen nicht die Erkenntnis der Realität ist, sondern die Durchsetzung der relativistischen Perspektive (so nachzulesen schon bei Einsteins geistigem Ziehvater Ernst Mach, 1883). Dieses ideologische Ziel wird mit allen (!) Mitteln der Rabulistik sowie der Verdrehung von physikalischen und historischen Fakten angesteuert. Schlichtweg ignoriert wird die Jahrhunderte alte wissenschaftliche Erkenntnis von der Bedeutung des Schwerezentrums oder “Baryzentrums” der Mehrkörpersysteme (wie das Sonnensystem eines ist) als Dreh- und Angelpunkt zur Beschreibung der Bewegungen von Planeten und Sonnenmittelpunkt um dieses Zentrum (Newton, Principia, Buch I Corollar 4 zu den Gesetzen). Die Einsteinschen Theorien kennen nichts dergleichen. Auch suche man einmal in diesem Blog nach dem Stichwort “Baryzentrum” oder “Schwerezentrum” oder “Schweremittelpunkt”. Das Ergebnis ist immer negativ. Der Verfasser (und der Blog, und die Einsteinsche Relativitätstheorie) weiß nichts davon, dass schon bei Copernicus die Himmelskörper nicht um die Sonne, sondern um dieses ruhende Zentrum kreisen. Er weiß nicht, dass Kepler irrig die Sonne für das ruhende Zentrum hielt (woraus dann die “Kepler-Ellipsen” um die Sonne hervorgingen). Er weiß nicht, dass Galilei gegen Kepler an der richtigen Copernicanischen Sichtweise festhielt. Und er weiß nicht, dass auch Newton Copernicus und Galilei folgte; Newton, der geometrisch zeigte, welche mathematischen Beziehungen zwischen den scheinbaren Kepler-Ellipsen um die Sonne und den wirklichen Kreisbahnen (!) um das Baryzentrum des Systems bestehen. Der Verfasser kennt nicht den Unterschied zwischen dem Scheinbaren (z. B. der Bewegung der Sonne vom Morgen zum Abend) und dem Wirklichen (der Bewegung der Erde und des Sonnenmittelpunkts um das Schwerezentrum des Systems), mit der die moderne Astronomie begann, als Copernicus die Wahrheit der Bewegung der Erde um den ruhenden Schwerpunkt des Systems erkannte. Er weiß nichts von der Bedeutung des ruhenden Bezugssystems, relativ zu dem wirkliche Bewegungen allein zu bestimmen sind. Wie alle Relativisten hält der Verfasser dieses Blogs die Copernicanische Sichtweise und die Ptolemäische Lehre von der Bewegung der Sonne um die Erde für “gleich richtig” (Ernst Mach 1883, Albert Einstein 1938). Natürlich bleibt dabei die Erkenntnis der Wirklichkeit auf der Strecke, die so ist, wie sie ist, und nicht so, wie einer sie gerne hätte. Und natürlich wird der Wahrheitsanspruch der Wissenschaft verabschiedet, wenn man die Frage, was da richtig ist und was nicht, dahinstehen lässt. Deshalb nochmals: Dem Verfasser dieses Blogs geht es nicht um die Wirklichkeit und Wahrheit, sondern um die Durchsetzung der relativistischen Ideologie. Also Vorsicht! Und, im Sinne der wahren Aufklärung: Selber denken!
Gut, Warnung abgesetzt, damit hat der Spuk hier hoffentlich ein Ende. Und Tschüß!
Meine Gegenwarnung: Offenbar hat Herr Dellian keine Ahnung von dem, was ich weiß und was nicht.
Wer nach einer Definition von “Rabulistik” sucht: dass Herr Dellian in diesem Blog zwar nach “Baryzentrum”, “Schwerezentrum” und “Schweremittelpunkt” suchen lässt (gibt’s auf meinem Blog in der Tat nicht), aber nicht nach dem weitaus üblicheren “Schwerpunkt” (der kommt vor und wird erklärt), wäre ein schönes Beispiel dafür: in “spitzfindiger […] Weise argumentier[en] und dabei […] den wahren Sachverhalt verdreh[en]”.
@Ed Dellian;
Offenbar haben Sie noch nicht darüber nachgedacht, dass das Schwerezentrum des Sonnensystems gar kein Schweresystem und kein Ruhepol ist, denn das gesamte Sonnensystem bewegt sich in der Milchstraße und diese bewegt sich durch das Universum, relativ zu anderen Galaxien. Ihre ganze Argumentation ist daher ein Schuss in den Ofen. Es ist typisch für die Gegner der ART, dass sie sich Modellsituationen ausdenken, die auch ohne die ART lösbar scheinen. Damit soll suggeriert werden, dass die ART eine unnötige Erschwernis darstellt oder sogar falsche Resultate liefert. Dabei erkennen sie nicht die Falschheit und Unvollständigkeit ihrer eigenen Prämissen und Behauptungen.
Angesichts der Unbelehrbarkeit, des Starrsinns und oftmals der Überheblichkeit der notorischen ART-Gegner oder ART-Dilettanten sind solche Diskussionen in der Regel einfach sinnlos.
@Anton Reutlinger: Schon Galilei lehrt das Relativitätsprinzip der Bewegung: Wirkliche Bewegung kann nur relativ zu wirklicher Ruhe festgestellt werden. Wenn das Sonnensystem als Ganzes einschließlich der Milchstraße sich “relativ zu anderen Galaxien” bewegen sollte, wie Sie meinen, so müssten diese Galaxien wohl ruhen. Der Relativismus lehrt aber das Gegenteil, nämlich die “Flucht” der Galaxien. Aber – relativ zu welchem Ruhesystem “fliehen” sie wohl? Keiner weiß es. Also weiß keiner, was sich da wirklich bewegt. Anderes gilt von der Realität des Baryzentrums des Sonnensystems als Ruhepunkt, relativ zu dem alle Bewegungen in diesem System zuverlässig bestimmt werden können. Dieser Ruhepunkt ist die selbstverständliche Grundlage der modernen extraterrestrischen Navigation, in Einsteins Terminologie “Anfangspunkt des Koordinatensystems”. Relativ zu diesem werden in der Praxis die Bewegungen von Objekten im Raum gemessen. Darüber kann man sich informieren, wenn man sich unter dem Stichwort “Baryzentrum” schlau macht. Pössels Blog kennt diesen elementaren astronomisch-physikalischen Terminus technicus nicht, weil der Verfasser davon nichts weiß – oder es verschweigt, weil es in die Einsteinsche relativistische Ideologie nicht passt. Wer das nicht-materielle Baryzentrum als ruhenden Punkt im Raum für einen Widerspruch zur Einsteinschen Lehre hält, hat freilich Recht. Beides kann nicht zugleich richtig sein. Was ist Wahrheit? Wer macht da der unendlich ahnungslosen Welt etwas vor? Albert Einstein, O-Ton: “Zwei Dinge sind wohl unendlich: Das Weltall und die menschliche Dummheit. Bezüglich des Weltalls bin ich mir aber nicht ganz sicher”. Auch das kann man wohl als Aufforderung lesen, nicht einfach zu glauben, was irgendein angebliches Jahrtausendgenie sich ausgedacht hat.
Wieder freche Rabulistik von Herrn Dellian, der entweder nicht versteht oder absichtlich ignoriert, dass in einem allgemeinverständlichen Text der Begriff “Schwerpunkt” nun einmal angebrachter ist als das Fremdwort “Baryzentrum”.
Zur kosmischen Expansion: Die kosmologischen Modelle benötigen als Grundlage nichts weiter als die Aussage, dass (und wie) sich die gegenseitigen Entfernungen der Galaxien ändern.
Und die moderne Physik kann mit unterschiedlichen Koordinaten zu denselben Vorhersagen kommen – ein in irgendeiner Form vor allen anderen Koordinatennullpunkten ausgezeichneter Ruhepunkt ist für die Vorhersagen nicht nötig. Und die Vorhersagen stimmen nun einmal, im Gegensatz zu dem von Ihnen auf Newton zurückgeführten Modell konzentrischer Kreise, exzellent mit den Beobachtungen überein.
Was Sie zur Irreführung Ihrer Leser als “Newtons Modell konzentrischer Kreise” bezeichnen, ist in Wahrheit kein “Modell”, sondern die erfahrbare, erfahrene und geometrisch strikt bewiesene Realität der Umlaufbahnen von Körpern um einen “gemeinschaftlichen Schwerpunkt” (Newton, Principia, Corol. 4 zu den Gesetzen), welche Körper einer zu diesem Schwerpunkt hin gerichteten “Zentripetalkraft” unterliegen, die mit dem Quadrat der Entfernung vom Schwerpunkt abnimmt. Siehe dazu Newton. Principia, Buch I Abschnitt II Lehrsatz 1, Lehrsatz 4 mit Corol. 6 und Scholium (ausdrücklich für die Umlaufbahnen der Himmelskörper), Lehrsätze 57 und 58 Corol. 2). Jedes rotierende kreisrunde Rad führt übrigens seit dessen Erfindung jedermann, der guten Willens ist, die Richtigkeit der Feststellung vor Augen, dass das Zentrum der Umlaufbewegung ein ruhender (oder gegebenenfalls geradlinig-gleichförmig im Raum bewegter) nicht-materieller Punkt ist, niemals ein “Zentralkörper”, wie ihn die Einsteinsche allgemeine Theorie – als Potential- und Gravitationstheorie! – entgegen Ihrer Behauptung immer voraussetzt. Sie wissen es besser, Herr Pössel! Sie argumentieren unredlich! Ich äußere mich dazu hier nicht mehr.
Wie schon kurz erwähnt: Ich hatte mir damals ja die Mühe gemacht, anhand der entsprechenden Ephemeridenprogramme des JPL nachzurechnen, wie groß die Abweichung der Planetenbahnen von konzentrischen Kreisbahnen um den Sonnensystem-Schwerpunkt ist. Da kamen Abweichungen heraus, die selbst Amateurastronomen direkt nachweisen könnten. Und die den Astronomen, die eben dieses Ephemeridenprogramm mit hochgenauen Beobachtungen immer wieder auf die Probe stellen, garantiert nicht entgangen wären, da sie um Größenordnung oberhalb der Genauigkeit der Beobachtungen lagen.
Insofern: Sorry, aber das entsprechende Modell (!) scheitert kläglich an den Beobachtungsdaten und ist damit für die Physik bzw. die Astronomie vom Tisch.
Das hatte ich Ihnen damals per E-Mail ja auch mitgeteilt, zusammen mit den Informationen, die es Ihnen ermöglicht hätten, meine Behauptung durch eigene Rechnungen zu überprüfen. Dass Sie damals an dieser Überprüfung nicht interessiert waren, aber jetzt hier auf so wackeliger Basis groß von angeblicher “Irreführung” und “Unredlichkeit” meinerseits tönen, ist schon, diplomatisch ausgedrückt, ein wenig dreist.
Sie haben es immer noch nicht kapiert, oder Sie wollen es nicht kapieren (was ich eher annehme): Die Beschreibung der Umlaufbahnen um das – nicht beobachtbare! – Schwerezentrum des Sonnensystems ist kein Gegenstand der astronomischen Phänomenologie (d. h. der Beobachtung), ebenso, wie schon die Erdumlaufbahn nicht astronomisch zu beobachten ist. Deshalb ist es unsinnig, aus astronomischen Beobachtungsdaten durch Ephemeridenrechnung die geometrische Form der Umlaufbahnen um das Schwerezentrum ermitteln zu wollen. Der Zusammenhang zwischen den unstreitig beobachtbaren elliptischen Umlaufbahnen um die Sonne und den nicht beobachtbaren exakten Kreisbahnen um das Baryzentrum ist ein geometrischer: Die Durchmesser von Kreis und Ellipse und die Umlaufzeiten auf diesen Bahnen sind, wie Newton mathematisch beweist, für jeden Planeten die gleichen. Die wahre Kreisform der Umlaufbahnen um das Baryzentrum erkennt nur, wer die mechanischen Prinzipien kennt und respektiert, nach denen ein Körper auf geschlossener Bahn um einen Punkt läuft, zu dem hin eine mit dem Abstandsquadrat abnehmende Zentripetalkraft wirkt, die den Körper von seiner tangentialen Bahn ablenkt und in eine Umlaufbahn um den Schwerpunkt zwingt. Hätten Sie Newton jemals studiert, dann wüssten Sie’s. Wenn Sie Newton studiert haben sollten, dann bestreiten Sie es hier wider besseres Wissen.
Aus astronomischen Beobachtungsdaten (Positionsbestimmungen von der Erde aus plus direkte Entfernungsbestimmungen über Radarsignale oder über Raumsonden) ist es möglich, die Positionen der Planeten im Sonnensystem genau zu bestimmen. Aus den Bahnbewegungen, den Raumsondenbewegungen und sogar mithilfe des Gravitationslinseneffekts lassen sich die Massen der Planeten bestimmen. Wer alle Massen und deren Positionen kennt, kann die Lage des Schwerpunkts eines Systems ausrechnen. Und kann in diesem Falle, elementare Geometrie, berechnen, wie sich die Positionen der Planeten in Bezug auf diesen Schwerpunkt ändern. Das Ergebnis: Es stimmt nicht, dass sich die Positionen der Planeten in Bezug auf den Schwerpunkt so ändern, als würden sich die Planeten mit konstanter Winkelgeschwindigkeit auf konzentrischen Bahnen um den Schwerpunkt bewegen. Das sagt mir der erwähnte Vergleich aufgrund der JPL-Ephemeriden, in die all diese Beobachtungs- und Messdaten einfließen.
Insofern: Doch, die Vorhersagen des Modells, das Sie hier propagieren, kann man sehr wohl mit den astronomischen Beobachtungs- und Messdaten vergleichen. Und Ihr Modell scheitert bei diesem Vergleich. Es ist nicht mit den Beobachtungs- und Messdaten vereinbar.
@Ed Dellian;
Warum sollte ich denn ausgerechnet Ihrem “Jahrtausendgenie” glauben? Eine gekrümmte Linie kann auf kurzen Strecken durch Geraden angenähert werden, genauso die Zeit, um zu einfachen Lösungen zu kommen. Solche vereinfachten Lösungen können für die meisten Situationen, insbesondere für die kurze Lebenszeit und die geringen Geschwindigkeiten des Menschen, ausreichend sind, aber es bleiben eben Annäherungen. Deshalb kann sich die bemannte Raumfahrt ohne Probleme mit Newton begnügen, wogegen für die Präzision des GPS bereits die Berücksichtigung der Relativität notwendig ist.
Das heißt, die Theorie der Relativität hat für alle Situationen Gültigkeit, im Gegensatz zu spezifischen Lösungen für spezifische Situationen. Das gilt für jede naturwissenschaftliche Theorie. Wollte man auf die allgemeine Theorie verzichten, dann müsste man für jede spezifische Situation jeweils eine eigene Theorie entwickeln. Das wäre dann keine Wissenschaft, sondern schlicht Pfusch mit hoher Fehleranfälligkeit. Für die praktische Wissenschaft und Technik haben spezifische Lösungen selbstverständlich ihre Berechtigung.
Ein Ruhezentrum im Universum ist eine Illusion, beruhend auf den menschlichen Alltagserfahrungen. Manche Leute können sich davon offensichtlich nicht lösen.
@Ed Dellian;
Was wollen Sie eigentlich mit dem Baryzentrum? Das ist ein alter Hut ohne wissenschaftliche Bedeutung, denn die Massen im Sonnensystem sind ungleich verteilt und sie bewegen sich ständig, so dass es weder ein gleichbleibendes Baryzentrum noch ein Ruhezentrum gibt. Mit der Anwendung der ART hat das ohnehin nichts zu tun. Offenbar geht es Ihnen nur um Ihre theistisch begründete und naiv realistische Ideologie, um Absolutheit von Raum und Zeit, die Sie mit Zähnen und Klauen verteidigen wollen.
Die Naturwissenschaft hat sich von diesem unnötigen Ballast endlich befreit. Man kann auch die Naturwissenschaft als Glaube oder als Weltanschauung verstehen, das entspricht der Meinungsfreiheit oder der Überzeugung des Skeptikers, aber die praktischen Erfolge und die Zuverlässigkeit der methodisch gewonnenen Erkenntnis zur Bereicherung und Verbreitung von Wissen sprechen ihre eigene Sprache. Wissen ist die Grundlage für die Bewältigung und die Gestaltung des Lebens. Mythen und Märchen können gelegentlich hilfreich sein, entbehren aber allgemein der Zuverlässigkeit.
@Pössel: Man kann nicht “die Positionen der Planeten im Sonnensystem genau bestimmen”, ohne zunächst die Lage des Baryzentrums zu kennen, relativ zu dem diese Positionen bestimmt werden sollen. Man kann also nicht (wie Sie meinen) aus Positionen der Planeten die Lage des Baryzentrums “berechnen”, um dann die Form der Umlaufbahnen zu ermitteln. Sie schreiben jetzt reinen Unsinn. Ich geb’s an dieser Stelle endgültig auf.
Selbstverständlich kann man solche Positionen bestimmen. Nicht jederzeit, dazu sind die Entfernungsmessungen nicht häufig genug. Aber sobald sie sowohl eine Entfernungsmessung für einen Planeten haben (z.B. durch das Transponder-Signal einer dort befindlichen Raumsonde) als auch die Richtung des Planeten von der Erde aus haben (Kugelkoordinaten), haben Sie die Position eindeutig bestimmt, rein geometrisch.
Richtungsinformationen (wo stehen die Planeten am Himmel?) haben die Astronomen dann noch deutlich mehr. Das sind insgesamt mehr als genug Informationen, um mithilfe der auf dem Newtonschen Gravitationsgesetz basierenden Dynamik alle Positionen im Sonnensystem zu rekonstruieren (und diese Beschreibung dabei auch noch streng auf die Probe zu stellen!), dann die Position des Schwerpunkts in Abhängigkeit von der Zeit zu berechnen und dann eben den Test durchzuführen, den das von Ihnen propagierte Modell nicht besteht.
Warum sollte man dazu die Lage des Baryzentrums vorab kennen müssen? In der üblichen, euklidischen Geometrie kann ich mir aussuchen, wohin ich meinen Koordinatennullpunkt lege. Und sobald ich die Lage aller Körper zu jedem gegebenen Zeitpunkt ermittelt habe, kann ich ausrechnen, welche Lage dieselben Körper zu jedem Zeitpunkt relativ zu einem anderen Bezugspunkt haben. In diesem Falle eben des rechnerisch ermittelten Baryzentrums.