Bei meiner Vorlesung Rote Riesen, Schwarze Löcher – woher wissen wir das alles? über Methoden der Astronomie (für Nicht-Physiker) wurde es letzten Donnerstag zwischenzeitlich statistisch. Ich habe versucht, nachvollziehbar zu machen, warum Astronomen darauf aus sind, ihre Aufnahmen mit möglichst großen Teleskopen durchzuführen und möglichst lange zu belichten. Das hat einiges mit einem der elementarsten Versuche der Statistik zu tun: “wiederholte Münzwürfe”.

Wahrscheinlichkeit für Münzwürfe

Wahrscheinlichkeit ist gar nicht so einfach zu definieren, und die Definition führt auch heute noch zu einigermaßen kontroversen Diskussionen. Was Münzwurfe angeht, ist die Argumentation dabei noch relativ einfach. Ein Ereignis, das sicher eintritt, bekommt die Wahrscheinlichkeit 1 zu gewiesen. Hat ein Zufallsversuch nur zwei mögliche Ergebnisse, dann müssen sich deren Wahrscheinlichkeiten zu 1 addieren (denn dass der Versuch zu einem der beiden Ergebnisse führt, ist unter diesen Umständen sicher). Bei einer fairen Münze soll die Wahrscheinlichkeit, dass die Münze nach einem Wurf “Kopf” (beim Euro: Brandenburger Tor) zeigt, per Definition genau so groß sein wie die Wahrscheinlichkeit, dass die Münze “Zahl” zeigt. (Dass die Münze nach dem Wurf auf dem Rand balancierend stehen bleibt, vernachlässigt man bei derartigen Betrachtungen üblicherweise.) All das zusammengenommen ergibt, dass die Wahrscheinlichkeit für “Kopf” gerade 0,5 beträgt. “Zahl” ist genau so wahrscheinlich.

Wahrscheinlichkeit gegen Häufigkeit

Mit der Wahrscheinlichkeit Kopf 50%, Zahl 50%, verbindet sich die folgende Erwartung: Wirft man eine faire Münze einige Male hintereinander, dann sollte in etwa in der Hälfte der Fälle “Kopf” herauskommen. Auch in der Statistik heißt der Wert 1/2 N Erwartungswert für die Anzahl der Fälle von “Kopf” bei N Würfen.

Das “in etwa” hat es allerdings in sich. Ich habe jetzt nicht eifrig Münzen geworfen, sondern, das sollte im Prinzip auf dasselbe hinauslaufen, meinen Computer Zufallszahlen 0 und 1 erzeugen lassen, jeweils mit derselben Wahrscheinlichkeit. “1” soll dem Fall entsprechen, dass meine virtuelle Münze “Kopf” zeigt.

Das folgende Diagramm zeigt auf der waagerechten Achse die Anzahl der durchgeführten Würfe, auf der senkrechten Achse die Anzahl der Male, die “Kopf” herauskam. Die blaue Kurve entspricht meiner Computersimulation, die rote dem Erwartungswert: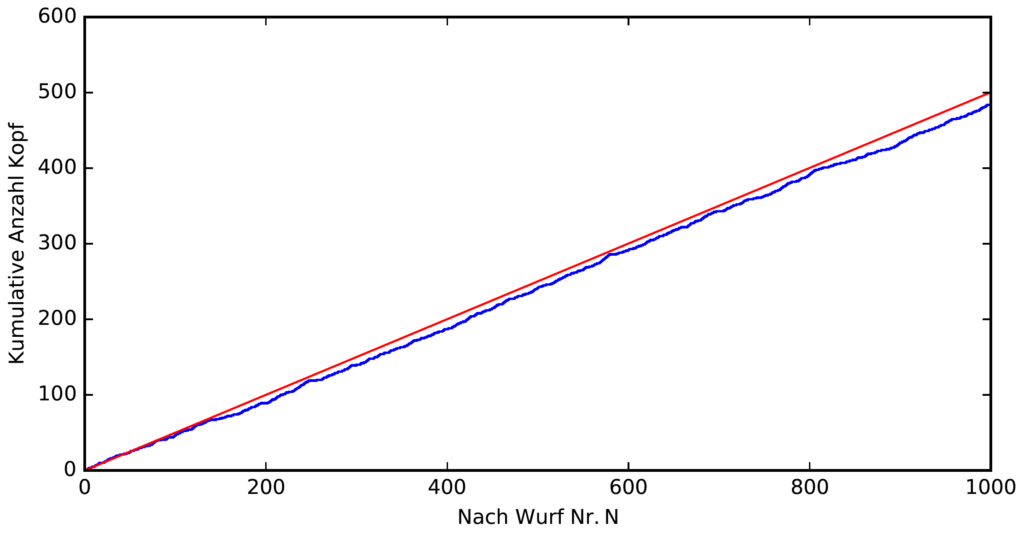Wenn nach jeder Anzahl von Würfen (oder zumindest nach jeder geraden Anzahl) exakt die Hälfte der Würfe “Kopf” gezeigt hätte, läge die blaue Kurve exakt auf der roten Kurve (der Geraden mit Steigung 1/2). Aber offenbar liegt die blaue Kurve etwas darunter – und entfernt sich sogar während der Versuchsreihe weiter von der roten Kurve.

Zunehmende Abweichungen

Dass sich die blaue Kurve mit der Zeit von der roten entfernt, ist zumindest zum Teil direkt plausibel. Genauer: Plausibel ist, warum die blaue Kurve es, kam es zu einer Abweichung, schwierig hat, zur roten Kurve zurückzufinden. Denn angenommen, die blaue Kurve sei bereits etwas unterhalb der roten Kurve zu liegen gekommen (sprich: es gibt insgesamt etwas weniger Male “Kopf” als erwartet). Die Wahrscheinlichkeit der nachfolgenden Münzwürfe bleibt davon unbeeinflusst. Insbesondere hat die Münze keinen eingebauten Trend, ein Defizit nach Möglichkeit auszugleichen. (Die gegenteilige Erwartung, etwa dass nach einer Reihe von “Zahl”-Ergebnissen die Wahrscheinlichkeit für ein “Kopf”-Resultat beim nächsten Wurf steigt, heißt “Gambler’s Fallacy”, im deutschen etwas trocken Spielerfehlschluss.)

Führt man diese Überlegungen mathematisch näher aus, dann kommt man darauf, dass es auch für die Größe der Abweichung von der Soll-Kurve (Hälfte Kopf!), für die Fluktuationen einen Erwartungswert gibt. Der liegt bei \(1/2\cdot\sqrt{N}\). In dem nachfolgenden Diagramm ist auf der waagerechten Achse wieder die Anzahl \(N\) der bereits erfolgten Münzwürfe eingetragen, auf der senkrechten Achse diesmal die Abweichung der aktuellen Anzahl von “Kopf”-Ergebnissen vom Erwartungswert \(|\overline{N}-N|\) (Absolutwert, sprich: ohne Vorzeichen), und in lila der Erwartungswert \(1/2\cdot\sqrt{N}\) jener Abweichungskurve: 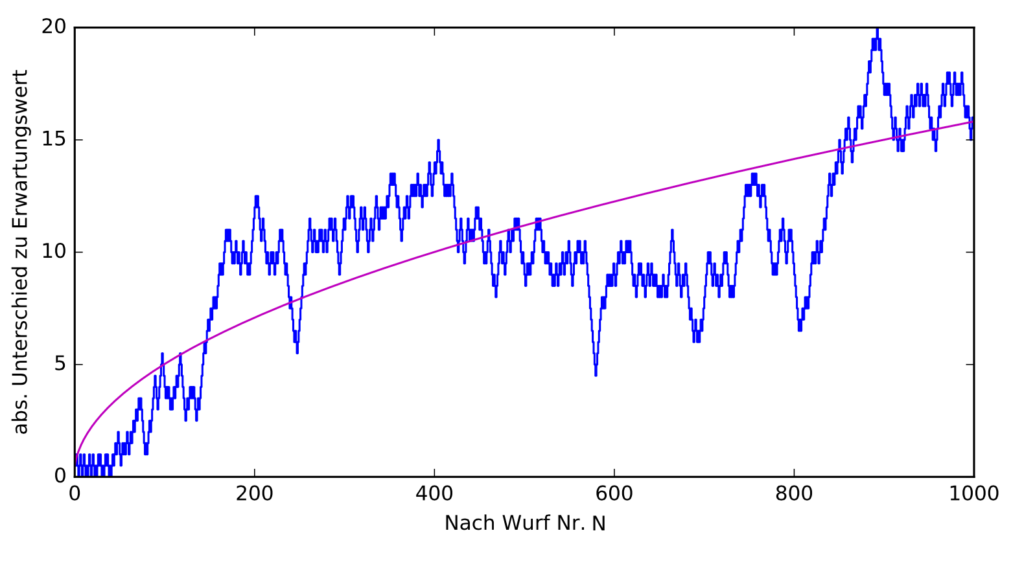Das kommt einigermaßen hin, aber auch um diese Abweichungskurve gibt es sichtbar Zufallsschwankungen – das liegt in der Natur der Sache!

Von der Häufigkeit zur Wahrscheinlichkeit

Können wir alleine aus unseren Wurfversuchen abschätzen, wie wahrscheinlich es ist, mit unserer Münze “Kopf” zu werfen? Mit anderen Worten: Können wir experimentell, mithilfe wiederholter Wurfversuche, Hinweise darauf finden, wie groß die Wahrscheinlichkeit für “Kopf” oder “Zahl” ist?

Für die Abschätzung ziehen wir die relative Häufigkeit \(H\) heran, also denjenigen Anteil an Münzwürfen, der in unserer Versuchsreihe in der Tat “Kopf” gezeigt hat. Dieser Anteil ist die Anzahl der “Kopf”-Ergebnisse, die wir erworfen haben, geteilt durch die Anzahl unserer Wurfversuche.

Im Idealfall entspräche die Anzahl der “Kopf”-Ergebnisse gerade dem Erwartungswert der “Kopf”-Anzahl, und wir hätten
\(H = \frac{1/2\cdot N}{N} = 1/2,\)
also in der Tat genau die erwartete Wahrscheinlichkeit.

Für eine reale Messung erwarten wir dagegen, dass die Anzahl der “Kopf”-Ergebnisse vom Erwartungswert um \(1/2\cdot\sqrt{N}\) abweicht. Für die relative Häufigkeit, also jene Anzahl geteilt durch \(N\), kann man zeigen, dass man erwarten muss, dass sie um \(1/2\cdot\sqrt{N}/N = 1/(2\sqrt{N})\) von der Wahrscheinlichkeit des “Kopf”-Ergebnisses abweicht. (Diese Größe, erwartete Abweichung durch Erwartungswert der Größe selbst, heißt Variationskoeffizient.)

Das sind gute Neuigkeiten, denn das heißt ja: Je mehr Versuche wir durchführen, je größer also \(N\) ist, umso geringer ist die erwartete Abweichung der relativen Häufigkeit von der “Kopf”-Wahrscheinlichkeit. Im Grenzfall unendlich vieler Versuche sollte die relative Häufigkeit von der wahren “Kopf”-Wahrscheinlichkeit dann gar nicht mehr zu unterscheiden sein. (Diese Aussage ist ein Spezialfall des sogenannten Gesetzes der großen Zahlen.)

In unserer Reihe von 1000 Versuchen sieht man diese Annäherung auch; der graue Bereich zeigt dabei die erwartete Abweichung der relativen Häufigkeit von der Wahrscheinlichkeit, die blaue Kurve die tatsächliche Situation nach \(N\) Versuchen: 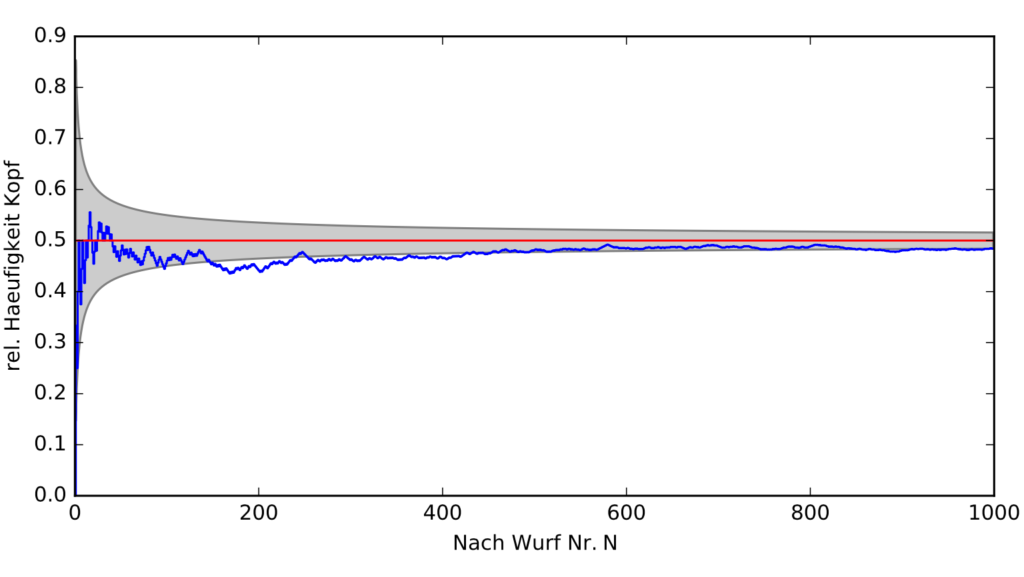Da zeigt sich mit der Zeit durchaus eine Annäherung. Der grau hinterlegte Bereich wird von den Erwartungswerten der Abweichung (zwei Kurven, da Abweichung nach unten und nach oben möglich) begrenzt.

Photonen und Astronomie

Was das ganze mit Astronome zu tun hat? Man kann sich das Licht, das an einem Teleskop ankommt, als Strom von Lichtteilchen, von Photonen vorstellen (genaueres findet sich in meinem Beitrag Was ist eigentlich Licht?) Gehen wir einmal vereinfacht davon aus, dass jedes dieser Lichtteilchen die gleiche Menge an Energie mitbringt. Sammelt das Teleskop für eine Zeit \(T\) (=Belichtungszeit) alles einfallende Licht, nämlich insgesamt \(N\) Photonen, dann entspricht das einem durchschnittlichen Photonenfluss von \(\Phi = N/T\).

Angenommen, wir haben eine konstant helle Quelle, sprich: eine Quelle, deren Helligkeit sich mit der Zeit nicht verändert. Die Helligkeit entspricht einem kostanten, durchschnittlichen Photonenfluss \(\overline{\Phi}\), analog zu der konstanten Wahrscheinlichkeit von 50% für die “Kopf”-Würfe im Münzwurfbeispiel.

Jetzt geht es wiederum darum, die Helligkeit zu messen, sprich: den Wert von \(\overline{\Phi}\) aus dem gemessenen Fluss abzuschätzen.

Unsere Abschätzung für den wahren durchschnittlichen Photonenfluss war \(\Phi = N/T\). Aber die Photonen, die das Teleskop erreichen, tun das nicht planmäßig – etwa in Reih und Glied, in exakt gleichem Abstand – sondern zufällig. Wir können im voraus nicht exakt angeben, wieviele Photonen das Teleskop in einer gegebenen Zeit \(T\) erreichen werden, sondern lediglich die Wahrscheinlichkeit dafür, dass eine bestimmte Anzahl von Photonen ankommt.

Ganz analog zum Münzwurf heißt das: Der Erwartungswert \(\overline{N} \equiv \overline{\Phi}\cdot T\), wieviele Photonen in einem Zeitintervall das Teleskop erreichen und registriert werden, wird in der Regel vom gemessenen Wert \(N\) abweichen. Rechnet man mithilfe der sogenannten Poisson-Statistik nach, dann zeigt sich, dass die zu erwartende Abweichung proportional zur Wurzel von \(\overline{N}\) ist, analog zum Fall des Münzwurfs. Abschätzen können wir die erwartete Abweichung durch unsere gemessene Photonenzahl; bei \({N}\) nachgewiesenen Photonen rechnen wir mit einer Abweichung von schätzungsweise \(\sqrt{N}\) Photonen.

Was bedeutet das für unsere Abschätzung des Photonenflusses, \(\Phi = N/T\)? Bei unserer Messung ist \({N}\) proportional zur Belichtungszeit \({T}\), denn bei (einigermaßen) konstantem Photonen-Nachschub gilt: Je länger wir den Photonen Zeit lassen, um bei unserem Teleskop anzukommen, umso mehr Photonen können wir insgesamt sammeln. Die erwartete Abweichung des Photonenflusses vom wahren Durchschnittswert ist damit proportional zu \(\sqrt{N}/T\sim \sqrt{N}/N = 1/\sqrt{N}\). Da haben wir’s: Wer Helligkeitswerte möglichst genau messen will, sollte möglichst viele Photonen sammeln. Dass die Astronomen immer größere Teleskope bauen, ist keine überbordende Technikbegeisterung, sondern hat einen soliden physikalisch-statistischen Hintergrund!

(Was dieser Hintergrund mit astronomischen Bildern, dem Nachweis von Objekten und dem Begriff des Kontrasts zu tun hat? Das ist einen weiteren Blogbeitrag wert…)