Von Bellschen und Rindlerschen Lokomotiven
Ich muss ehrlich gestehen, dass ich von den Reaktionen auf meinem Artikel zur materiellen Seite der Längenkontraktion etwas überrascht wurde. Selbst Kommentatoren, die mir bisher nicht als Kritiker der Relativität aufgefallen waren, zeigten sich verwundert, dass die spezielle Relativität tatsächlich Auswirkungen auf Beschleunigungsvorgänge haben könnte.
Dabei bin ich den diesem Artikel nur einen kleinen Schritt über die übliche relativistische Kinematik hinausgegangen und habe ein wenig Dynamik eingeführt. Wie ich hier schon oft herausgestellt habe, braucht es keineswegs die Allgemeine Relativitätstheorie um Beschleunigungen zu verstehen. Die Spezielle Relativitätstheorie benutzt Koordinatensysteme wie die Newtonsche Physik: Als eine Art Bühne, auf der die Natur stattfindet. Nur dass die Regeln dieser Bühne etwas andere sind. Das macht sich besonders bei hohen Geschwindigkeiten bemerkbar. Kräfte haben zusätzliche geschwindigkeitsabhängige Komponenten, wenn sie von schnellen Objekten ausgehen.
Das zeigt sich eben auch in der Längenkontraktion. Wir wissen aus der rein kinematischen Betrachtung in Einsteins ursprünglicher Publikation, dass bewegte Objekte kürzer sind als identische Objekte in Ruhe. Das ist kein optischer Effekt aufgrund der Lichtlaufzeiten. Im Gegenteil, dieser Effekt ist erst erkennbar, wenn die Lichtlaufzeiten herausgerechnet werden oder man im Gedankenexperiment eine laufzeitfreie Messung durchführt. Zum Beispiel durch gleichzeitige Positionsbestimmungen von beiden Enden des Objektes.
Gedankenexperiment: Zug und Bahnhof
Nehmen wir das berühmte Bahnhofbeispiel:
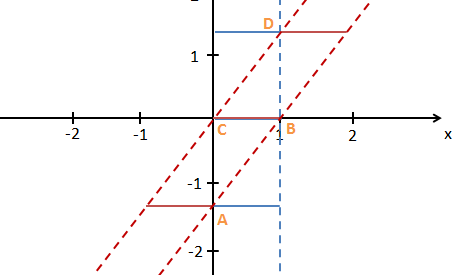
Wenn durch einen Bahnhof von 100 m Länge ein Zug mit 80% Lichtgeschwindigkeit durchfährt, so dass Zugspitze und Zugende gleichzeitig auf Höhe von Ende und Anfang des Bahnsteigs sind, dann ist der Zug in seinem Eigensystem 500/3=167 Meter lang und die Insassen bemessen die Länge des Bahnsteigs auf nur 300/5=60 Meter. Ein am Bahnhof ruhender Zug gleicher Bauart und Konfiguration würde aber um 2/3 über den Bahnhof hinausragen und tatsächlich auch 167 Meter lang sein.
Die Frage ist nun, was es für den zunächst ruhenden Zug bedeutet, wenn er auf 80% Lichtgeschwindigkeit beschleunigt wird. Wir sind uns hoffentlich einig, dass er hinterher genauso lang sein sollte, wie der bereits fahrende Zug.
Bellsche Raumschiffe
Das Bellsche Raumschiffparadoxon ist ein erster Ansatz, diese Frage zu durchdringen. Bell stellte die Frage, was mit einem Seil passieren müsse, dass zwischen zwei gleichartig und gleich stark beschleunigten Raumschiffen gespannt ist. Dieses Seil solle die wundersame Eigenschaft haben, zwar jede beliebige Beschleunigung einfach mitzumachen aber sofort zu reißen, wenn es gezwungen wäre, sich zu verlängern.
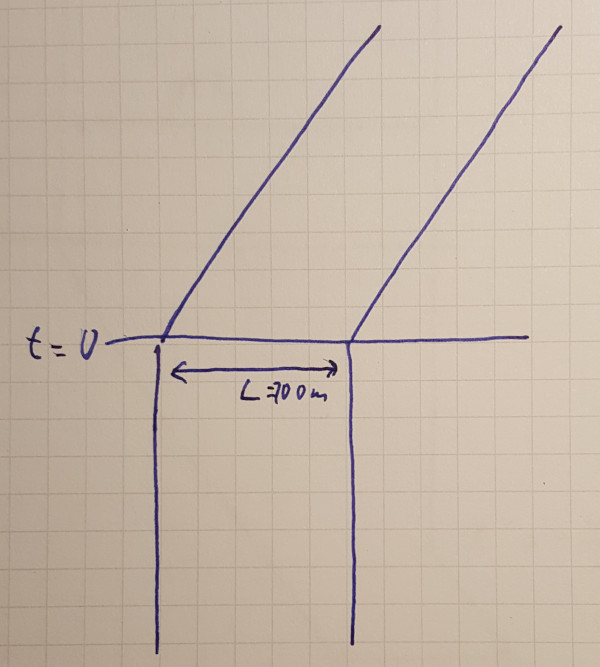
Das schöne an diesem Gedankenexperiment ist, dass wir nur wenig zu rechnen haben. Wir können die beiden identischen Beschleunigungsmanöver als instantane Änderungen der Geschwindigkeit zu einem Gemeinsamen Zeitpunkt t=0 in den Ausgangskoordinaten annähern. Zu Zeiten vor der Beschleunigung t<0 sollen sich Raumschiffe zueinander ruhen, nach der Beschleunigung bewegen sich beide mit 80% Lichtgeschwindigkeit. Das hintere Raumschiff soll vor der Beschleunigung am Ort x=0 ruhen, das vordere am Ort x=L mit L=100 Meter.
Transformation in das neue Ruhesystem
Möchte wir nun sehen, wie die Situation in einem Koordinatensystem aussieht, in dem die Raumschife nach der Beschleunigung ruhen, können wir die Lorentztransformation anwenden:1
t’=5/3(t-vx/c²)
x’=5/3(x-vt)
Für das hintere Raumschiff ist nichts zu rechnen. x und t sind Null, also sind auch x’ und t’ Null. Für das vordere Raumschiff ist t=0 aber x=L:
t’=-(5/3)(4/5) L/c=-4/3 L/c
x’=5/3 L
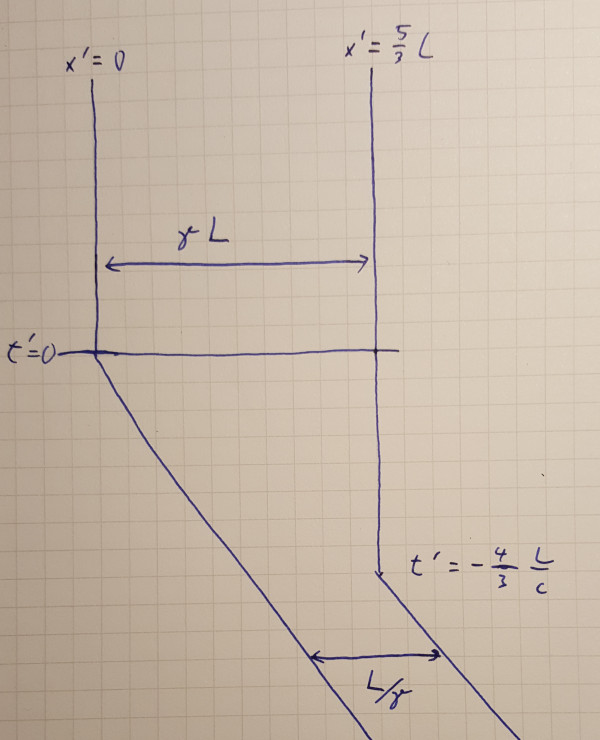
Da beide Raumschiffe nach der Beschleunigung zueinander ruhen, bedeutet x’=5/3 L=167 Meter, dass die Raumschiffe nach der Beschleunigung tatsächlich weiter als die ursprünglichen 100 Meter voneinander entfernt sind. Das Seil reißt also.
Der Grund dafür liegt in t’=-4/3 L/c. Die Beschleunigung des vorderen Raumschiffs geschieht zu negativer Zeit vor der Beschleunigung des hinteren. Zwischen t’= -4/3 L/c und T’=0 bewegt sich das vordere Raumschiff mit 80% Lichtgeschwindigkeit und das hintere ruht. Kein Wunder, dass das Seil reißt!
L/c ist die Zeit, die Licht braucht, um die Strecke L zu durchqueren. Ein mit 80% Lichtgeschwindigkeit reisendes Raumschiff legt in dieser Zeit die Strecke 80% L, also 4/5 L zurück. In der Zeit 4/3 L/c, legt das Raumschiff die Strecke (4/3)(4/5)L=16/15 L zurück. Wenn die Raumschiffe nach beiden Beschleunigungen 5/3 L voneinander entfernt sind, waren sie also vor der ersten Beschleunigung (5/3-8/15)L=(25-16)/15 L=3/5 L voneinander entfernt. Das ist, wie zu erwarten, genau die Lorentz-kontrahierte Entfernung der Raumschiffe in ihrem ursprünglichen Ruhesystem.
Um es zusammenzufassen: Werden in einem Koordinatensystem zwei Raketen genau gleichzeitig mit identischen Manövern in einem Abstand von L gestartet, dann ist ihr Abstand in ihrem neuen Ruhesystem nach der Beschleunigung um den Faktor Gamma länger. Vor der ersten Beschleunigung war er um denselben Faktor kürzer. Das ist deshalb möglich, weil die Beschleunigungen in ihren neuen Ruhesystem nicht gleichzeitig erfolgen.
Zur Rindler-Beschleunigung
Durch ein abgewandeltes Manöver lässt sich die Situation ändern: Beschleunigt man das hintere Raumschiff noch immer instantan, das vordere aber in zwei Schritten, so lässt sich erreichen, dass die Raumschiffe im neuen Ruhesystem denselben Abstand haben, wie vor den Beschleunigungen im alten.

Links im Bild ist das durch die gestrichelte Weltlinie angedeutet. Die vordere Rakete beschleunigt zur Zeit t’=-4/3 L/c so, dass sie zur Zeit t’=0 den Abstand x’=L erreicht. Dort wird ihre Geschwindigkeit dann endgültig an die des hinteren Raumschiffs angeglichen.
Wie ich in der Diskussion des vorherigen Artikels bereits ausgeführt habe: Um nach der Beschleunigung denselben Ruheabstand wie vorher zu erreichen, muss das vordere Raumschiff ein längeres Manöver mit geringeren Beschleunigungswerten durchführen.
Dieses Prinzip können wir weiter führen, indem wir die gestrichelte Gerade zwischen den beiden instantanen Beschleunigungen durch eine Kurve ersetzen. Das aus zwei einzelnen instantanen Beschleunigungen bestehende Manöver des vorderen Raumschiffs wird so zu einer ausgedehnten Beschleunigung.
Wählen wir die gestrichelte Linie nun so, dass sie eine Hyperbel bildet, so könnte die Beschleunigung an jedem Punkt abgebrochen werden und die nun geradlinig weiterfliegenden Raumschiffe hätten gleiche Entfernungen. Das Seil würde nicht reißen.
Dass es sich bei der Linie um eine Hyperbel handeln muss, liegt daran, dass die Hyperbel eine Linie ist, die den Wert x²-c²t² konstant hält. Und genau das ist die Eigenlänge eines Objektes.
Rindler Koordinaten
Solche Hyperbel-Bahnen zusammen mit den Gleichzeitigkeits-Strahlen ausgehend vom hinteren Raumschiff können auch als Koordinaten eines gemeinsam beschleunigten Objektes dienen. Man bezeichnet diese Koordinaten nach Wolfgang Rindler als Rindler-Koordinaten2.
In diesen Koordinaten ist der Nullpunkt, also der Punkt, an dem unser hinteres Raumschiff sitzt, eine sogenannte Singularität. Hier schneiden sich alle Zeit-Koordinatenlinien. Die Zeit steht still. Das liegt daran, dass wir dem hinteren Raumschiff einen unendlichen Beschleunigungswert zugewiesen haben. Um zu einer realistischen Betrachtung zu kommen, müssen wir beide Raumschiffe etwas nach rechts vom Nullpunkt wegrücken.
Dann erhalten wir zwei Raumschiffe, die auf unterschiedlichen Hyperbelbahnen beschleunigen. Das hintere Raumschiff mit einem stärkeren Beschleunigungswert, dafür aber etwas kürzer. Betrachten wir das kurz nochmal in drei Koordinatensystemen:
Im Ausgangs-Ruhesystem starten die beiden Raumschiffe gleichzeitig ihre Beschleunigung. Das hintere beschleunigt dabei stärker als das vordere. Letzteres braucht also länger um die Endgeschwindigkeit zu erreichen. Beide Raumschiffe beschleunigen auf Hyperbel-Bahnen und nach Abschluss der Beschleunigungen ist ihre Entfernung um den Faktor 1/Gamma verkürzt. Das Seil hält.
Im End-Ruhesystem beenden die beiden Raumschiffe gleichzeitig ihre Beschleunigung. Das vordere Raumschiff hat aber früher begonnen und beschleunigt weniger stark. Beide auf Hyperbel-Bahnen. Vor der Beschleunigung war der Abstand um den Faktor 1/Gamma verkürzt, hinterher ist er so, wie vorher im Ausgangssystem. Das Seil hält.
In Rindler-Koordinaten behalten die Raumschiffe die ganze Zeit ihren Abstand bei. Das Seil hält. Falls die Raumschiffe Uhren mitführen, geht die hintere Uhr langsamer als die vordere. Alle physikalischen Prozesse laufen hinten langsamer ab als vorne, deshalb muss dort heftiger beschleunigt werden um mitzuhalten. Hier kommen wir schon fast in die Allgemeine Relativitätstheorie. Aber nur fast. Die Raumzeit ist noch immer flach. Wir beschreiben sie nur in krummen Koordinaten.
Zurück zu den Zügen
Und was hat das nun mit der materiellen Seite der Längenkontraktion zu tun? Starre Objekte zeichnen sich dadurch aus, dass die ihre Länge beigehalten. Das geht aber nicht ohne ein wenig Elastizität. Was auf leichte Dehnung oder Stauchung nicht mit einer Rücktreibenden Kraft, einer Spannung reagiert, muss brechen wie das Bellsche Seil.
Der Bellsche Zug wäre ein Zug mit zwei Loks an den Enden, die identische Beschleunigung erzwingen. Dieser Zug wäre nach vollbrachter Beschleunigung im neuen Ruhesystem im den Faktor Gamma gestreckt. Vornehmlich in den Kupplungen zwischen den Wagen.
Im Rindlerschen Zug würde die vordere Lok weniger stark aber länger beschleunigen als die hintere. Beide würden zueinander passende Hyperbeln in der Raumzeit beschreiben um die Spannungen in den Kupplungen auf Null zu halten. Ganz geht das aber nicht, die Trägheitskräfte zerren ja noch immer an den Wagen, nur die zusätzliche Verspannung durch Lorentzkontraktion würde durch die stärker drückende hintere Lock ausgeglichen.
Der realistische Zug dagegen wird von vorne gezogen. Er dehnt sich unweigerlich ein wenig und die dadurch in den Kupplungen entstehenden Spannungen treiben die Wagen an. Ebenso wird sich eine durch ein hinten angetriebenes Triebwerk beschleunigte Rakete unweigerlich ein wenig stauchen. Die Verspannung durch diese Stauchung treibt die vorderen Teile und die Spitze an.
Die Aussage der SRT ist nun, dass es zur Newtonschen Trägheit eine zusätzliche Kraft gibt, die beim relativistischen Zug durch stärkere Verspannung, eine stärkere Beschleunigung des letzten Wagens erzwingt. Und die in der relativistischen Rakete die Spannung ein wenig verringert, weil vorne eine geringere Beschleunigung ausreicht um den Gleichgewichtsabstand zu halten.


Na, geht doch prima 😉 aber (schon wieder Hooke?)
wird wohl nicht auf allgemeinen Beifall stoßen, auch die Wagen müssen Gamma.
Das Beispiel gibt es auch zu Ehrenfest, und zwar Backsteine auf einer Rotierenden Scheibe.
Zwei Meinungen: a) der Abstand zwischen den Steinen kontrahiert, weil die Steine “starrer” sind.
b) Egal ob Abstand oder Stein, für beides gilt Gamma. Wer weiß was anderes oder besser?
Gamma ist ein Geschwindigkeitseffekt und wird nicht durch Hooke ausgeglichen oder?
PS: im Nachhinein ist mir noch ein “halb”relativistischer Pferdefuß zum Gedankenexperiment eingefallen.
Die Dehnung Gamma ist ein metrologischer Effekt aufgrund der Gleichzeitigkeitsbedingung häppchenfrei.
So gesehen betrifft die Längenänderung gleichermaßen Wagens und Kupplungens ohne(?) Unterschied.
Aber wegen ΔF=k*Δx impliziert im Kräftevergleich eine Streckung eine Kraft auf die Materialkonstante k.
Die Frage ist nicht, ob im (noch) gekoppelten System (schon) unterschiedlich gedehnt wird, sondern was
zuerst reißt, hier die Kupplungen als schwächstes Glied. Die Wagens werden gedehnt wie die Abstände.
Joachim schrieb (29. Okt 2019):
> […] Die Frage ist nun, was es für den zunächst ruhenden Zug bedeutet, wenn er
… bzgl. der verbleibenden Mitglieder des Inertialsystems, zu dem der Zug zunächst ebenfalls gehörte …
> auf 80 % Lichtgeschwindigkeit beschleunigt wird. Wir sind uns hoffentlich einig, dass er hinterher genauso lang sein sollte, wie der bereits fahrende Zug.
Ob ein Zug, dessen Bestandteile (und insbesondere dessen beide Enden) erst (einzeln) aus ihrer gegenseitigen Ruhe gerissen, und letztlich wieder zu gegenseitiger Ruhe gebracht wurden, hinterher genauso lang sein sollte wie vorher, oder wie ein momentan mitbewegter ruhender Zug, oder wie irgendein anderer Zug, darauf mögen sich Ingenieure festlegen.
Grundlegender ist, dass sich überhaupt Versuch für Versuch messen lässt, ob ein Zug nach derartiger Behandlung jeweils genauso lang war wie vorher, oder wie ein momentan mitbewegter ruhender Zug, oder wie irgendein anderer Zug; oder in wie fern nicht.
> […] zwei Raumschiffe, die auf unterschiedlichen Hyperbelbahnen beschleunigen. […] Das hintere beschleunigt dabei stärker als das vordere.
Bei geeigneten jeweils konstanten Beschleunigungsbeträgen (b bzw. a), in Abhängigkeit von den gegenseitigen Ping-Dauern (τB_AB bzw. τA_BA),
a / b =
Exp[ -a/c τA_(BA) ] =
Exp[ -b/c τB_(AB) ] =
(τB_(AB) / τA_(BA)) = konstant,
bzw. in Abhängigkeit von der (konstanten) Distanz L jeweils zwischen den beiden Mitgliedern eines momentan mitbewegten Inertialsystems, die die Passage/Umkehr des vorderen und die Passage/Umkehr des hinteren Raumschiffs gleichzeitig anzeigten,
1/b – 1/a = c^2 / L = konstant,
spricht man von “chronometrisch starrer Beschleunigung” bzw. von “Born-starrer Beschleunigung”.
Frank Wappler schrieb (29.10.2019, 16:31 Uhr):
> Bei geeigneten jeweils konstanten Beschleunigungsbeträgen (b bzw. a) […] in Abhängigkeit von der (konstanten) Distanz L jeweils zwischen den beiden Mitgliedern eines momentan mitbewegten Inertialsystems, die die Passage/Umkehr des vorderen und die Passage/Umkehr des hinteren Raumschiffs gleichzeitig anzeigten,
> 1/b – 1/a = c^2 / L = konstant, […]
Stattdessen (d.h. für Born-starre Beschleunigung):
1/b – 1/a = L / c^2 = konstant;
vgl. https://arxiv.org/abs/1105.3899 (J. Franklin, “Rigid body motion in special relativity”), Gleichung 14.
@Herr Senf
Klar wirken sich die kinematischen Effekte auf Kupplung und Wagen gleichermaßen aus. Aber die Kupplungen sind in der Regel flexibler als die Wagenwände. Die beiden Loks sollen in diesem Gedankenexperiment den Zug auf die Länge GammaL halten. Wenn wir einen Zug so auseinander ziehen, bin ich sicher, dass die Kupplungen stärker gedehnt sein werden, als die Wagenwände.
Zu deinem P.S.
Nein, Gamma ist zwar ein kinematischer Effekt, aber Beschleunigung braucht Kräfte. Das Vakuum hat keine Fixpunkte. Nur wenn wir tatsächlich jedes einzelne Atom anpacken und beschleunigen könnten, würde sich alles gleichmäßig auseinander ziehen. Können wir aber nicht. Wir haben immer bestimmte Angriffspunkte unseres Antriebs und dazwischen herrscht Materialspannung. Zwei Loks sind Fixpunkte. Was dazwischen passiert, entscheiden Hooke und Newton (Trägheit).
“Nur wenn wir tatsächlich jedes einzelne Atom anpacken und beschleunigen könnten, würde sich alles gleichmäßig auseinander ziehen. Können wir aber nicht. Wir haben immer bestimmte Angriffspunkte unseres Antriebs und dazwischen herrscht Materialspannung. ”
was ist mit Gravitation?
@zabki
Das ist ein guter Punkt. Die Gravitation greift natürlich jedes einzelne Atom an, weil sie keine eigentliche Kraft, sondern Ausdruck verzerrter Raumzeit ist. Allerdings ist Gravitation kaum als Antrieb zu verwenden, weil sie nicht einfach geschaltet werden kann. Natürliche Gravitationsfelder treten ja zumeist Kugelsymmetrisch auf und dann beschleunigen sie gerade das vordere Raumschiff stärker als das hintere. Das heißt, sie erzeugen selbst Kräfte zwischen den Atomen.
@Joachim
Es überrascht, was Dich überrascht. Du produzierst hier weiterhin widersprüchliche Aussagen zur Länge Deines 167 Meter langen und mit β=4/5 inertial bewegten Zuges, der, wie es Dir gerade passt, entweder 100 Meter lang sein soll, wegen materieller Längenkontraktion, oder wahlweise 278 Meter, falls er sich dararn erinnert, dass er irgendwann zuvor in einem Bahnhof still auf dem Gleis gestanden hat.
Und dann wundert es Dich, dass Du Dir dafür kritische Kommentare einhandelst? Unbedarfte Laien könnten bei Deinen Deutungen tatsächlich zu dem Eindruck gelangen, dass die ganze RT komplett gaga ist, und man kann eigentlich nur hoffen und beten, dass sie dann nicht die Theorie, sondern nur einige ihren beflissenen Erklärer für gaga halten. Frag’ doch mal Markus Pössel, ob er das mit Deiner “materiellen Seite der Längenkontraktion” versteht und ohne Wenn und Aber unterschreiben würde, was Du hier dazu präsentierst.
Zu Deiner Lorentz Transformation. Da hast Du praktisch nur die Koeffizienten des als Linearkombination in der Basis {∂t’,∂x’} dargestellten Vektors L∂x für Dein Beispiel mit β=4/5 bestimmt, also
L∂x = γL∂x’ − γβL∂t’,
und Dir daraus in einem Kurzschluss das γL als transformierten Lok-Abstand im gestrichenen System herausgelesen. Wer so etwas als Lösung für eine Übungs- oder Prüfungsaufgabe abliefert, erhält dafür leider null Punkte.
Willst Du also nochmals nochmals nachbessern, oder willst Du das so für die Nachwelt stehen lassen? Im Bedarfsfall liesse sich auch eine Musterlösung für den Übergang von (t,x) zu (t’,x’) bei dieser “stosshaften Beschleunigung” hier zumindest skizzieren, aber das sollten auch Physiker doch eigentlich hinkriegen können.
Nun, Herr Senf hat ja hetzt verstanden, worauf ich hinaus wollte. Dass du eine eigentümliche Theorie vertrittst, wissen wir ja jetzt. Ich habe deinen Denkfehler schon in Eine Bewegung zu viel aufgeklärt.
Das sieht nach einem Druckfehler aus, auch wenn sich das wegen t=0 nicht auf das Ergebnis auswirkt. Korrekturvorschlag:
x’=5/3(x-vt)
Wo du recht hast, hast du recht.
Vielen Dank, ist korrigiert.
@Joachim / 01.11.2019, 21:34 Uhr
Es ist menschlich sehr verständlich, dass Dir in Kommentaren Zustimmung willkommener ist als Einspruch, aber Du tust im Moment verdammt wenig dafür, dass ich Dir zustimmen kann. Meiner unverhohlenen Aufforderungen, Deine Deutungen zur “materiellen Seite der Längenkontraktion” mit dem Relativitätsprinzip in Einklang zu bringen, bist Du nach wie vor nicht nachgekommen. Mach’ doch wenigstens mal einen ernsthaften Versuch, Deine Vorstellungen so darzulegen, dass sie möglichst nicht missverstanden werden.
Nach dem spez. Rel.prinzip ist es einzig eine Frage der Betrachtung, ob ein inertiales Objekt als “ruhend” oder als mit einer Geschw. β ≠ 0 “bewegt” angesehen wird, und ein Wechsel der Betrachtungsweise via Lorentz Transf. ändert an den physisch-materiellen Gegebenheiten für das in Betracht stehende Objekt absolut nichts. Damit ist Deine fett betonte Unterscheidung zwischen bewegten und unbewegten Ruhelängen aus dem letzten Blogartikel physikalisch irrelevant, da wird materiell nichts kürzer oder länger.
Und wenn Du jetzt meinst, in dem letzten Absatz einen Denkfehler entdecken zu können, dann sag’ mir doch bitte in möglichst unmissverständlichen Worten, worin der Deiner Meinung nach bestehen soll.
Du musst halt zwischen Koordinatenwechsel und Beschleunigung unterscheiden. Während erste die physikalische Situation natürlich nicht verändern können, können letzere es sehr wohl.
@Chrys
Das die ZD ein realer Effekt ist darüber sind wir uns einig oder?
So ganz spontan kann ich nicht erkennen warum die real sein sollte die LK aber nur ein Artefakt des Beobachterstandpunktes.
@Chrys (02.11.2019, 15:51 Uhr)
Mit der Lorentz-Transformation wird nicht nur die “Betrachtungsweise”, sondern auch das Inertialsystem gewechselt. Das ist physikalisch relevant. Damit ändern sich u.a. die Geschwindigkeit und die Gleichgewichtslänge des Objekts. In der SRT gilt als Maßstab das aktuell gewählte Bezugssystem.
Da war nicht von bewegter “Ruhelänge”, sondern von der “Gleichgewichtslänge” die Rede. Damit ist normalerweise die Länge des materiellen Objekts ohne äußere Krafteinwirkung gemeint.
Nach meinem Eindruck vermischt du verschiedene Bezugssysteme. Du argumentierst z.B. bei einem bewegten Objekt mit dessen Ruhesystem oder in dem neuen Inertialsystem nach einer Beschleunigung mit der Uhren-Synchronisierung in dem ursprünglichen Inertialsystem, welches du damit “absolut” setzt. Das ist aus meiner Sicht teilweise ein Rückgriff auf die Epoche vor dem Galileischen Relativitätsprinzip.
@Joachim @Anonym
SO ein bischen verstehe ich das Problem von Chrys schon. Mein Bauch sagt mir das wenn die ZD real ist auch die LK real ist. Was ich so für mich auch annehme, die ZD ist sehr schwer wegzudiskutieren 😉 Wie bekäme ich denn heraus Das auf ein Objekt wirklich eine Beschleunigung wirken würde? Und nicht nur eine Koordinatentransformation durchgeführt würde? Ich darf ja das Inertialsystem zB auf den Masseschwerpunkt legen und dann beschleunigt alles andere…
@Uli Schoppe (05.11.2019, 18:16 Uhr)
Beides sind relative Effekte und relative Effekte sind im gleichen Ausmaß “real” wie absolute Effekte.
Die Eigenbeschleunigung kann man mit einem Beschleunigungssensor messen.
Eine LK gibt es in beiden Fällen, siehe auch:
Quelle:
https://scilogs.spektrum.de/quantenwelt/die-materielle-seite-der-laengenkontraktion/#comment-38622
@Joachim / 02.11.2019, 20:27 Uhr
Die Kontraktion mit 1/γ wird auch von Dir als Konsequenz eines Lorentz Boosts präsentiert — da ist noch alles inertial und nichts beschleunigt. Wo Lorentz das gemacht hat, unterscheidet er zwischen “im Aether ruhend” und “im Aether bewegt”, wobei er dem Aether eine physische Qualität zuschreibt, mit der er eine physisch-materielle Verschiedenheit dieser beiden Fälle begründet. Diese Argumentation lässt sich für die SRT aber nicht übernehmen, mangels Aether, weshalb Markus Pössel dann auch sagt, dass die Lorentz Kontraktion keine materielle Veränderung inertial bewegter Objekte impliziert.
Mein Vorschlag wäre noch, Du vergleichst die RDT* für Lichtsignal Roundtrips von der hinteren Lok zur vorderen und wieder zurück, einmal im alten Ruhe-System mit (t,x) und dann im neuen mit (t’x’). Wenn der Lok-Abstand in neuen rest frame ein anderer ist als im alten, müssen auch die Messwerte verschieden sein, und das muss sich auch rechnerisch erhalten lassen.
Ist der Übergang von (t,x) zu (t’,x’) ein Lorentz Boost, kommt in beiden Fállen der gleiche Messwert heraus.
* RDT = Round-trip Delay Time. Ist der IT Terminus für “Pingdauer” und schneller getippt.
Ich bin hier nicht an der Round-Trip-Delay-Time interessiert. Die ergibt immer die Eigenlänge eines Objektes. Hier geht es aber darum, wie lang das Objekt in einem Inertialsystem ist, in dem es nicht ruht. Diese Länge ist immer um den Faktor 1/Gamma kürzer als die Eigenlänge. Dazu braucht es keinen Äther, sondern schlicht die Lorentz-Symmetrie der Naturvorgänge.
Der Springende Punkt in diesem Artikel ist aber, dass die Verkürzung eines Objektes bei Beschleunigung nicht einfach magisch passiert sondern durch zwischen-atomare Kräfte.
@Chrys (05.11.2019, 20:18 Uhr)
MP hat aber das aus dem Zusammenhang gerissene Zitat …
… bemängelt:
Quelle (s. weiter unten):
https://scilogs.spektrum.de/relativ-einfach/einstein-verstehen-ein-blogexperiment-teil-i/#comment-1955
Tja, die einfache Antwort:
Beobachtungsbedingte Phänomene – nicht Phänomene am Beobachtungsgegenstand.
Aber hier wird ja bewusst die Wahrheit unterdrückt.
Ja, nicht einmal zur Diskussion gestellt. Denn die Wahrheit ist entwaffnend einfach.
Alles bestens dokumentiert, Herr Schulz.
Haben Sie eigentlich schon ein Erdloch ausgewählt, worin Sie sich dann verkriechen können, wenn es so weit ist? Wenn offenbar wird, dass Sie hier als aktiver Unterdrücker der Wahrheit fungieren.
Beobachtungsbedingte Phänomene sind es ja gerade nicht:
Eine Koordinatentransformation ändert nicht eine einzige Beobachtung.
Beschleunigungen erzeugen Trägheits-Effekte die sich nicht als beobachtungsbedingt bezeichnen lassen.
Beobachtungsbedingt wären beispielsweise Laufzeiteffekte, die werden aber in der Längenkontraktion herausgerechnet.
@Joachim / 05.11.2019, 21:15 Uhr
Um Dein Gedächtnis vielleicht etwas aufzufrischen, im Blogtext schreibst Du
»Da beide Raumschiffe nach der Beschleunigung zueinander ruhen, bedeutet x’=5/3 L=167 Meter, dass die Raumschiffe nach der Beschleunigung tatsächlich weiter als die ursprünglichen 100 Meter voneinander entfernt sind.«
Da die Beziehung zwischen altem und und neuem rest frame ein Boost ist — wie Du es für Deine Rechnung auch verwendet hast — ermitteln die Loks (oder andere Vehikel) jedoch nach der Beschleunigung noch immer 100 Meter als ihren Abstand, und nicht 167 Meter. Du hast da keinen Rechenfehler gemacht, aber Du hast Dich mit Projektion und Transformation verheddert.
Nehmen wir nun zu Deiner Bahnhof-Betrachtung an, der Zug sei, zunächst auf dem Gleis stehend, 167 Meter lang. Er werde dann auf β=4/5 “Bell-beschleunigt”, meinetwegen auch idealisiert stosshaft, das stört hier nicht. Nach Deiner Rechnung sollte er in seinem (t’,x’)-Frame ruhend dann wohl 278 Meter lang sein und passt mit einer kontrahierten Länge von wieder 167 Metern jedenfalls nicht in den 100 Meter langen Bahnhof. Da seine Ruhe-Länge im (t’,x’)-Frame korrekterweise aber nur 167 Meter beträgt, würde er auf dann nur 100 Meter kontrahiert gerade so in den 100-m-Bahnhof hineinpassen.
Na, wie wllen wir das jetzt auflösen? Passen 167 Meter Bell Train in 100 Meter Bahnhof — oder doch eher nicht?
Ja, das ist korrekt:
Würde man einen Zug Meter langen Zug mit beiden Loks oder meinetwegen sogar alle Atome gleichartig beschleunigen, so bliebe die Länge im Ursprünglichen (t,x) Sytem gleich. Ein 167 Meter langer mit v=4/5 bewegter Zug ist in seinem Ruhesystem 278 Meter lang (Längenkontraktion). Nun hat er aber nur Atome für 167 Meter, also passiert eines der Folgenden Dinge:
1) Der Zug ist nicht elastisch genug und bricht bei der Beschleunigung auseinander.
2) Der Zug ist superelastisch und zieht sich auf seine Gleichgewichtslänge von 167 Metern gemessen im neuen Ruhesystem zusammen.
In Fall 2) ist der Zug nach der Kontraktion im Bahnhofssystem 100 Meter lang.
@Joachim
Die nachfolgende und mit einer Frage verknüpfte Überlegung möchte ich Dir noch nahebringen.
Vom Bahndamm aus betrachtet ist mit den Koord. (t,x) für t ≥ 0 die Bewegung der stosshaft beschleunigten Loks schon fast klassisch (bis auf die relativist. Bedingung |β| < 1), nämlich
x(t,ξ) = ξ + βt
als Lösung der klass. Bewegungsgl. d²x/dt² = 0 zur Anfangsbed. x(0,ξ) = ξ, dx(0,ξ)/dt = β, und, sagen wir, ξ = 0 für die hintere und ξ = L für die vordere Lok. Dann gilt noch folgendes:
Erstens ist es für diese Bahndamm-Darstellung des Geschehens offenbar völlig egal, was die Uhren in den bewegten Loks anzeigen, und im Bahndamm-System wird sich der Lok-Abstand gewiss nicht dadurch spontan ändern, dass die Lokführer ihre Uhren wie auch immer neu einstellen. Die Anzeige der Lok-Uhren ist von Belang für die Darstellung im Ruhe-System der bewegten Loks mit den Koord. (t',x'), aber das ist für Lok-Abstände oder Zug-Längen im Bahndamm-System unerheblich.
Zweitens lassen sich die obigen Lösungen x(t,ξ) auch für t < 0 fortsetzen. Ein Beobachter am Bahndamm, der da geschlafen hat und erst irgendwann später die Loks in Bewegung sieht, kann observationell nicht mehr herausfinden, ob sie bis t = 0 auf dem Gleis standen und dann stosshaft beschleunigt wurden, oder ob sie schon immer mit der konstanten Geschw. β auf dem Gleis unterwegs waren.
Unser verschlafener Beobachter kann noch konstatieren, dass er in jedem dieser Fälle für t < 0 den Lok-Abstand L gefunden haben würde, hätte er das nicht verpennt, und dass beide Fälle zu den ihm aktuell vorfindlichen physikal. Gegebenheiten führen. Die Beschleunigung hat keine ihm feststellbaren Effekte hinterlassen, und er kann fürderhin auch so tun, als habe sie nie stattgefunden.
Wie das alles für die Loks aussieht, sei erst mal zurückgestellt. In Hinblick auf die Frage nach der Beurteilung von Länge bewegter Züge bzw. von Abstand bei bewegten Lok-Paaren im Bahndamm-System wäre meine Frage zunächst, ob Du bis hierhin zustimmst.
Nein. Ich stimme in einem Punkt nicht zu: Ob es an Bord der Loks Uhren gibt und was die anzeigen ist in jedem Fall egal. Wie kommst du auf:
“Die Anzeige der Lok-Uhren ist von Belang für die Darstellung im Ruhe-System der bewegten Loks mit den Koord. (t’,x’)” Wofür sollte der Uhrenstand relevant sein?
@Chrys (07.11.2019, 16:03 Uhr)
Bis auf die Kleinigkeit, dass der Zug in der Mitte durchgerissen wurde. Die Lücke zwischen den beiden jeweils Lorentz-kontrahierten Zughälften sollte auch dem verschlafenen Beobachter am Bahndamm auffallen.
@Joachim / 07.11.2019, 16:18 Uhr
Die Systemzeit eines Inertialsystems ist per definitionem durch die Anzeige von dort ruhenden und synchronisierten Uhren gegeben (Einstein 1905, §1). Für den neuen rest frame der Loks mit den Koordinaten (t’,x’) ist t’ die Systemzeit, und die Lok-Uhren sind die einzigen in Frage kommenden Uhren, um diese Systemzeit anzuzeigen. Die beiden Loks mit ihren Uhren sind die konstituierenden Bezugsobjekte dieses Frames, und auch wenn etwa Wagons als weitere System-Komponenten hinzugedacht werden, dann doch stets in ihrer zeiträumlichen Relation zu den Loks.
Sorry, aber das ist Quatsch.
Die Systemzeit eines Inertialsystem ist eindeutig über die Postulate der SRT definiert und kann durch Lorentz-Transformation aus jedem beliebigen anderen Inertialsystem gewonnen werden. Dazu braucht es keine im System ruhenden oder gar synchronisierten Uhren.
@Joachim / 08.11.2019, 10:47 Uhr
Wenn ich Dir schon die Quelle nenne, dann schau doch wenigstens nach, was dort steht, falls es Dir nicht gegenwärtig sein sollte.
Dir entgeht offensichtlich völlig, dass der Übergang von (t,x) zu (t’,x’) infolge der Änderung des Bewegungszustandes der Loks auf dem Gleis eine aktive Transformation ist. Im Unterschied zur passiven Form wird dabei das gestrichene System nicht einfach als irgendwie gottgegeben angenommen, sondern erst durch die Konstruktion einer linearen Abbildung B erhalten, wobei die neue Basis {∂t’,∂x’} als Bild {B∂t,B∂x} der alten Basis bestimmt wird.
Ausgehend von den Lösungen x(t,ξ) lässt sich B konstruieren, indem zunächst mit t = γτ die Eigenzeit τ der Lok-Uhren eingeführt, oder, was laienhaft gesprochen dasselbe ist, eben die “Zeitdilatation” einbezogen wird, woraus sich durch anschliessende Synchronisierung t’ erhalten lässt, was schlicht heisst, dass die Anzeige der vorderen Uhr um den Clock Offset zurückgesetzt wird, den sie noch hat, wenn die Lok-Uhren τ anzeigen. Beide Schritte zusammen liefern B als einen Boost mit β.
Falls Dir das jetzt vorkommt wie böhmische Dörfer, was ich befürchte, solltest Du Dich vielleicht zunächst mit dem Unterschied zwischen aktiven und passiven Transformationen näher befassen, bevor Du grandios dazu kommentierst. Sofern Dir das nicht einleuchten will, auch gut, dann würde mich nur noch interessieren, wer Dich eigentlich auf die schräge Idee gebracht hat, die sogenannte Längenkontraktion habe etwas mit zwischen-atomaren Kräften zu tun. Einstein kann das jedenfalls nicht gewesen sein, das ist allemal gewiss.
@Chrys (06.11.2019, 16:37 Uhr)
Wie kann man sich damit verheddern? Die Projektion (“Gamma”-Faktor) ist Teil der Lorentz-Transformation. Durch die Projektion (“Gamma”-Faktor) und die Relativität der Gleichzeitigkeit (-v x /c²) unterscheidet sie sich von der Galilei-Transformation.
@Chrys (09.11.2019, 14:35 Uhr)
Die Lorentz-Transformation betrifft auch elektromagnetische Felder (Einstein 1905, §6):
https://de.wikibooks.org/wiki/A._Einstein:_Kommentare_und_Erl%C3%A4uterungen:_Zur_Elektrodynamik_bewegter_K%C3%B6rper:_Elektrodynamischer_Teil
Bell hat in Kapitel 9 ab Seite 68 die Auswirkung auf die Form der bewegten Atome berechnet:
https://is.muni.cz/el/1441/podzim2017/FY2BP_TF1/um/Uceni_text_-_John_S._Bell_Speakable_and_Unspeakable_in_Quantum_Mechanics__First_Edition.pdf#page=81&zoom=page-fit,-436,444
Ich denke, ich habe den Standpunkt der SRT im Artikel ausreichend deutlich beschrieben und muss das nicht im Kommentarbereich mehrfach wiederholen.
Bitte an die Diskutanten: Bleiben Sie am Ball und versuchen das durchzufechten.
Liegt zwischen Anonymus_2019 und Chrys nicht ein simples verbales Mißverständnis vor?
die elektromagnetischen Felder und die Atome “unterliegen” der Längenkontraktion, und grade deshalb “betrifft” sie diese nicht, denn sie “merken” davon quasi nichts.
Das gilt mal wieder nur für die Lorentztransformation und nicht für die oben beschriebene Bellsche Beschleunigung. Bei einer Lorentztransformation, also bei Änderung des Koordinatensystems, werden Felder und Koordinaten zugleich, also kovariant transformiert. Am Ende kommt für alle dasselbe raus, egal in welchen Koordinaten man rechnet. Bei gleicher Beschleunigung bleiben aber die Abstände gleich. Nur die Gleichgewichtslänge verkürzt sich. Das merken die Beschleunigten Objekte natürlich.
@Joachim
Wenn gar keine materiell gedachten Verbindungselemente zwischen die Loks eingehängt werden, dann ergeben sich nur rein geometr.-kinemat. Fragen nach Lok-Abstand, für die jegliche “zwischen-atomare Kräfte” doch offensichtlich völlig irrelevant sind.
Und wenn nun die Transformation, die den Wechsel der Loks von ihrem alten rest frame mit Koord. (t,x) in ihren neuen mit Koord. (t’,x’) beschreibt, ein Lorentz Boost ist, dann ermitteln die Loks in (t’,x’) den gleichen Abstand L wie zuvor in (t,x), denn ein Boost ist isometrisch. Der frommen Legende zufolge sollte dann aber im Bahndamm-System die Loks auf dem Gleis mit kontrahiertem Abstand L/γ fahren. Tun sie aber nicht, nach Voraussetzung.
Nach Deiner Lesart sollten daher die Loks in (t’,x’) ihren Abstand als γL ermitteln, aber auch das tun sie halt nicht. Wie passt das nun alles zusammen? Dieses Rätsel hast Du noch nicht gelöst.
Ach ja, ob ein schneller 167-m-Zug komplett in einen 100-m-Bahnhof passt, vielleicht guckst Du hier:
Cacioppo, R., & Gangopadhyaya, A. (2012). Barn and pole paradox: revisited. Physics Education, 47(5), 563-567. [Link]
Verhilft Dir das bei dieser leidigen Frage womöglich zu einer Einsicht?
Du langweilst mich, Chrys,
Nein, die Loks ändern ihre Geschwindigkeit nicht durch Lorentztransformation sondern durch Beschleunigung.
Ja, ihr räumlicher Abstand im Ausgangssystem bleibt gleich. Warum sollte er sich Ändern.
Nein, ein räumlicher Abstand ist keine Invariante bezüglich der Lorentztransformation. Der Lokabstand in ihrem neuen Ruhesystem ist GammaL.
Ja, das ergibt sich, indem man mit einem Lorentz-Boost ein neues gestrichenes Koordinatensystem (t’,x’) erzeugt, in dem die Loks ruhen.
Invariant bezüglich des Lorentz-Boosts ist die Größe s, definiert durch s²=x²-t². Zwei im ungestrichenen System gleichzeitige Ereignisse sind im gestrichenen nicht mehr gleichzeitig und haben einen größeren räumlichen Abstand.
@Joachim
Darauf wünsche ich aber schon eine vernünftige Antwort, was Du Dir erwartest, wie inhaltliche Einwände gegen Deine Ausführungen vorzubringen wären. Gewisse Reste an an wissenschaftl. Gepflogenheiten sollten bei dem Anspruch an wissenschaftl. Bloggen noch erkennbar bleiben, wozu gehört, dass man sich auch mit unbequemer Kritikt sachlich zu befassen bemüht, wenn diese berechtigt vorgebracht wird. Und dazu speziell nochmals:
Was es mit der Lorentz Kontraktion in der SRT auf sich hat, wurde von Minkowski vor gut 110 Jahren schon hinreichend dargelegt, und da braucht es keine Nachbesserung. Es ist nach wie vor überhaupt nicht plausibel, warum materielle Aspekte hierbei eine Rolle spielen sollten, zumal die Lorentz Kontraktion nicht nur mit materielle gedachten Objekten assoziiert wird.
Weiters sind Lorentz Transformationen lineare Isometrien des Minkowski Raumes, was insbesondere heisst, dass bei einem Lorentz Boost geometr. Abstände erhalten bleiben. Wenn Du schon einen Boost als Transf. der Loks vom ihrem alten in ihr neues Ruhe-System heranziehst, dann wird dabei ihr Ruhe-Abstand erhalten bleiben, worauf Du jedoch in keiner Weise eingehst.
Du musst nicht beständig wiederholen, was Du an Behauptungen schon gebracht hast, damit werden die genannten Unstimmigkeiten in Deinen Behauoptungen schliesslich nicht aus der Welt geschafft.
Deine Einwände habe ich längst zur Kenntnis genommen und in mehreren Artikeln beantwortet. Sie sind und bleiben falsch:
1. Ein Lorentz-Boost erhält nicht den räumlichen Abstand zweier Punkte, sondern den Raumzeit-(pseudo)-Abstand zweier Ereignisse. Dieser Pseudoabstand ist kein richtiger Abstand, er kann für unterschiedliche Ereignisse Null sein und er kann eine komplexe Zahl werden. Insbesondere ist er kein räumlicher Abstand, sondern die Differenz der räumlichen und zeitlichen Abstandsquadrate.
2. Zwei Objekte werden im Minkowskiraum nicht durch Punkte, sondern durch Weltlinien repräsentiert. Der Abstand zweier Linien ist im allgemeinen schwieriger zu definieren als der Abstand zweier Punkte. Ein eindeutiges Abstandsmaß gibt es nur nur bei Geraden. Das ist dann der Eigenabstand. Da die Weltlinien der Loks vor und nach der Beschleunigung je auf anderen Geraden liegen, ändert sich mit Beschleunigung auch der Eigenabstand.
Du hast recht, wir müssen das nicht ständig wiederholen. Deshalb beende ich die Diskussion hiermit.
@Joachim (12.11.2019, 14:27 Uhr)
Das gilt aber nicht, wenn man elektrische Felder und magnetische Felder separat über Dreier-Vektoren beschreibt:
Quelle:
http://www.itp.tu-berlin.de/fileadmin/a3233/lehrevorws06/lehress05/TPIII/lessonIX.pdf#page=8&zoom=auto,41,-93
Kovariant ist z.B. das elektromagnetische Viererpotential:
https://www.spektrum.de/lexikon/physik/kovariante-formulierung-der-elektrodynamik/8442
Ich sehe das ein bisschen anders:
Die Felder transformieren mit den Koordinaten, wie es die Natur eben vorgibt. Unabhängig davon, wie wir sie darstellen. In den kovarianten Darstellung, also über Tensoren, wird die Symmetrie des elektromagnetischen Feldes offensichtlich, weil die Gleichung forminvariant ist. Die Komponenten aber transformieren kovariant. Und aus den Komponenten des Vierervektors lassen sich die Dreiervektoren ausrechnen. Die transformieren also ebenso.
@Joachim (20.11.2019, 08:35 Uhr)
Dass die Aufteilung des em. Felds in Magnet- und elektrisches Feld vom Bewegungszustand des Beobachters abhängt, sieht man an folgendem Beispiel:
Quelle (Kapitel 4.2):
http://www.desy.de/~pschmues/Relativitaetstheorie.pdf#page=13&zoom=auto,-130,394
Natürlich hängt die Aufteilung des elektromagnetischen Feldes vom Bewegungszustand ab. Das ist aber unabhängig davon, ob wir diese Felder durch zwei dreidimensionale Vektoren oder einen vierdimensionalen Tensor beschreiben. In jedem Fall ändern sich die Komponenten mit dem Koordinatenwechsel. Deshalb heißt es ja kovariant und nicht invariant.
Invariant bezüglich der Lorentztransformation sind nur Skalare und Tensorgleichungen, nicht die Vierervektoren und Vierertensoren für sich.
Meine Verwunderung darüber, welche schier unüberwindlichen Klüfte sich hier auftun, ist schon beträchtlich, wobei es sich doch im wesentlichen gerade nur um lineare Algebra und ihre Anwendung in der Minkowski Geometrie dreht. Der anspruchsvollste Teil dabei sind lineare Tranformationen in zwei Dimensionen, zu deren Handhabung, wie man meinen sollte, eigentlich keine Fragen offen bleiben müssten. Das bewegt sich alles auf dem Niveau von Übungsaufgaben, wie sie auch mancherorts gestellt und bisweilen erfolgreich gelöst werden.
So etwa bei der Frage, wie lang im Bahndamm-Systm (t,x) ein Zug ist, der mit konstanter Geschw. β auf dem Gleis fährt und in seinem Ruhe-System (t’,x’) die Länge L habe. Das lässt sich beantworten, wenn an den beiden Enden des Zuges t-simultan jeweils Markierungen auf das Gleis gesetzt werden, deren Abstand dann im Bahndamm-System geometrisch zu messen ist. In (t’,x’) mögen die dort synchronisierten Uhren zunächst die System-Zeit t’ anzeigen, wobei dann relativ zu (t,x) eine weiter vorn befindliche Uhr nachgeht. Nun lässt sich die Anzeige der Zug-Uhren aber so verstellen, dass sie t-simultan, also bezogen auf (t,x), stets gleiche Werte anzeigen, wodurch sie im Zug-System desynchronisiert werden und dort eine weiter vorne befindliche Uhr dann vorgeht. Formal liefert der Lorentz Boost von (t,x) zu (t’,x’) dazu den Ansatz
t = γt’ + γβx’ = γ(t’ + βx’) =: γs,
der die lineare Transformation
t’ = s − γβq
x’ = γq
in die Koord. (s,q) motiviert, wobei der Faktor γ in der zweiten Gleichung garantiert, dass der Basisvektor ∂x’ in einen Einheitsvektor transformiert wird. Während die 4-Geschw. aller Zug-Uhren wegen ∂s = ∂t’ unverändert bleibt, wird der in (t’,x’) vom hinteren zum vorderen Ende des Zuges weisende Abstandsvektor L∂x’ transformiert in
L∂q = γL∂x’ − γβL∂t’ = L∂x.
Das ist dann der von der hinteren zur vorderen Markierung weisende Abstandsvektor, wenn diese an den beiden Enden des fahrenden Zuges bei einem Anzeigewert s der Zug-Uhren auf das Gleis gesetzt wurden. Die Markierungen haben den geometr. Abstand L und kennzeichnen die Positionen der Enden des Zuges, als die Bahndamm-Uhren den Wert t = γs anzeigten. Der Zug hatte demnach im Bahndamm-System in diesem Moment die Länge L.
Du bist ganz schön verzweifelt, oder?
Hier führst du also ein drittes Koordinatensystem (s,q) ein, dass dem gestrichenem System entspricht aber die Länge um den Faktor Gamma streckt. Die die Länge in (x,t) und (s,q) gleich ist, ist sie in (x’,t’) verkürzt. Das ist genau, was ich über mehrere Artikel schreibe.
Aber es ist doch viel einfacher: Die länge des Zuges im Zug und im Bahnhofsystem lässt sich im Minkowski-Diagramm ablesen. Findest du in jedem Lehrbuch.
@Chrys (21.11.2019, 13:16 Uhr)
Welche Länge hat der Zug dann im Zug-Ruhesystem (t’,x’), wenn man folgende Gleichungen von dir berücksichtigt?
und
P.S.
In deiner letzten Gleichung muss meiner Ansicht nach das “-“-Zeichen im mittleren Term durch ein “+”-Zeichen ersetzt werden. Grund:
@Anonym_2019 / 24.11.2019, 12:00 Uhr
Der Vektor ∂q hat die t’-Komponente ∂t’/∂q = −γβ und die x’-Komponente ∂x’/∂q = γ, was sich durch partielles Ableiten aus den Transformationsgl.
t’ = s − γβq
x’ = γq
ergibt. Daher das Minus-Zeichen bei
L∂q = γL∂x’ − γβL∂t’.
Die rechte Seite dieser Gl. hat man freilich auch, wenn der Lorentz Boost von (t,x) zu (t’,x’) invertiert wird. Der inverse Boost von (t’,x’) zu (t,x) dreht ∂x’ längentreu in ∂x, und die Transf. zu (s,q) verfährt mit ∂x’ auf genau die gleiche Weise.
Die Länge L des Zuges in seinem Ruhe-System (t’,x’) war hier als Voraussetzung angenommen. Wenn der Zug nun durch diese Transf. im Minkowski Raum längentreu “gedreht” wird, behält er diese Länge. Die Transf. modelliert ja auch nichts anderes als eine Manipulation mit den Anzeigen der System-Uhren des Zuges, wobei die Anzeige einer solchen Uhr gegenüber der System-Zeit t’ um so mehr vorgestellt wird, je weiter sie in Fahrtrichtung vom hinteren Zugende bei x’=0 entfernt ist.
P.S. Ich hatte inzwischen noch eine Erläuterung dazu gegeben, die durchaus für die allgemeine Leserschaft gedacht war, was allerdings, wie ich annehmen muss, annihiliert worden ist. Anlässlich der Rückfrage füge ich den Text hier nochmals mit der Mouse an:
Noch zur Erläuterung: Diese Transf. operiert in der (t’,x’)-Ebene, indem sie den Basisvektor ∂x’ in ∂x = ∂q dreht und dabei den Basisvektor ∂t’ = ∂s fix lässt. Das stellt als aktive Transf. im Minkowski Raum geometrisch den Akt einer Desynchronisierung der System-Uhren im fahrenden Zug durch Umstellung auf eine Bahndamm-simultane Anzeige dar. Einem im Zug mitgeführten Meterstab sind die Konventionen zu Uhr-Anzeigen herzlich egal, und er merkt gar nichts davon, ob er geometrisch mit ∂x’ oder mit ∂q identifiziert wird — so oder so sollte damit die gleiche Zuglänge L gemessen werden. Und das wird dann auch formal bestätigt durch die Beziehung
−||L∂q||² = [dq(L∂q)]² = [γ dq(L∂q/γ + βL∂s)]² = [dx'(L∂x’)]² = −||L∂x’||² = L².
Das Wesentliche an dieser Umstellung von Uhr-Anzeigen ist, dass man damit Bahndamm-simultane Ereignisse an den separaten Enden des fahrenden Zuges veranlassen kann, wie etwa zeitlich koordiniertes Setzen von Positionsmarken auf das Gleis, deren Abstand im Bahndamm-System (mit ∂x als geometr. “Meterstab”) anschliessend gemessen werden kann.
Du hängst noch immer an dem Irrtum, die Länge des Zuges in (x,t) sei durch denselben Vektor gegeben, wie die Länge in (x’,t’). Das ist nicht der Fall. Die zur Zugspitze gleichzeitigen Momente am Zugende sind verschiedene Ereignisse. Deshalb ist die Längenänderung nicht durch Drehung eines Vierervektors zu ermitteln.
Ich schließe die Diskussion hier ab, wir drehen uns im Kreis.
Chrys,
sind Sie noch immer derjenige Mathematiker, der die korrekte Störungstheorie für okkulten Symbolismus hält? Hier geht es weiter:
http://www.relativ-kritisch.net/blog/kritiker/wolfgang-engelhardt-unsinn-michelson-interferometer/comment-page-53#comment-31843
Bitte verteidigen Sie auf Relativ-Kritisch Ihre abwegige Behauptung, dass in Einsteins Artikel über die Perihelbewegung des Merkur in der Gleichung unterhalb von Gleichung (7c) (auf Seite 837) anstelle von 2A der Ausdruck 2A/(1-2A) stehen muss
Martin Raible
Ach, bitte verhandelt eure Dispute auf relativ-kritisch.net doch dort. Ich schalte das jetzt einmalig frei, möchte aber hier keine Quer-Diskussion von anderswo führen.
Mir sind zwei Fehler in dem Abschnitt “Transformation in das neue Ruhesystem” aufgefallen:
Zunächst heißt es: “Zwischen t’= -4/3 L/c und T’=0 bewegt sich das vordere Raumschiff mit 80% Lichtgeschwindigkeit und das hintere ruht. Kein Wunder, dass das Seil reißt!” Ich denke, wir wollen hier die Geschwindigkeiten in dem Bezugssystem ausdrücken, in dem die Raumschiffe nach der Beschleunigung ruhen. Denn wir benutzen ja die Zeit dieses Bezugssystems (t’ und nicht t). Es sollte daher heißen: “Zwischen t’= -4/3 L/c und t’=0 ruht das vordere Raumschiff und das hintere bewegt sich mit 80% Lichtgeschwindigkeit in negative x’-Richtung. Kein Wunder, dass das Seil reißt!”
Dann steht dort: “Wenn die Raumschiffe nach beiden Beschleunigungen 5/3 L voneinander entfernt sind, waren sie also vor der ersten Beschleunigung (5/3-8/15)L=(25-16)/15 L=3/5 L voneinander entfernt.” Da ist ein Tippfehler passiert. Es muss heißen: (5/3-16/15)L=(25-16)/15 L=3/5 L
Beschleunigungsfrei und mit c :=1:
Sei Bob – einmal mehr – mit konstantem β=4/5 von Sol nach α Cen, das im IS Σ_Sol im Abstand D=4.4 ly zu Sol ruht, unterwegs.
Alice, die im Inertialsystem Σ_A = Σ_Sol ruht, notiert (0, 0) – i.e. t = 0, x = 0 – für Bobs Vorbeiflug an Sol und (5.5, 4.4) für Bobs Vorbeiflug an α Cen. Mit β=4/5, γ = 5/3 transformiert das für Bobs Σ_B zu rund (10/3, 0).
Da Bob aber eben mit β=4/5 relativ zu Σ_Sol unterwegs ist, misst er dergestalt einen Abstand von rund 10/3 * 4/5 = 8/3 zwischen Sol und α Cen, was¹ der LK von 4.4 um 1/γ = 3/5 entspricht.
Wo bitte war da jetzt ein Problem mit der physischen Realität der LK?
¹ hier bis auf 1% Rundungsfehler.