Tropical Geometry is not about exotic rainforests
BLOG: Heidelberg Laureate Forum

Falko Gauss, HLF14 participant: As I am writing this text, I am actually supposed to prepare for the last two exams of my Master course. During my preparations it happened several times that I stumbled upon a name like Robert Tarjan. Robert Tarjan is a Nevanlinna Prize winner, a pioneer in graph theory algorithms and will attend the Heidelberg Laureate Forum 2014. Situations like that made me aware of what a great opportunity I have got to participate in the Heidelberg Laureate Forum and exchange ideas with all those great people.
In particular, I think that the Heidelberg Laureate Forum offers a unique platform to experience an exchange of ideas between the mathematical disciplines, between Mathematics and Computer Science, across the generations and between scientific heroes and newcomers. As one of the newcomers I am especially excited to get to know the laureates Shigefumi Mori, Michael Atiyah and Gerd Faltings. Those are laureates who accomplished eminent results close to my own field of research.
Currently my main interest lies in Tropical Geometry. What sounds like a subject dealing with exotic rainforests and sandy beaches is, in fact, a modern area of Algebraic Geometry. Since inope my opinion calling this subject “Tropical” is a little infelicitous, I don’t want to recall the story of the origin of this name here. But please feel free to find out yourself or just ask me at the Heidelberg Laureate Forum.

Credit: Dieter Schütz Pixelio.de
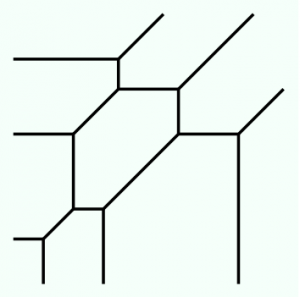
Credit: Kilom691 CC BY-SA 3.0
The key idea of Tropical Geometry is it to skeletonize algebraic varieties and transform them into combinatorial objects. In the combinatorial world things are usually easier to handle. This also applies to certain topological invariants, known as Gromov-Witten invariants. Those invariants play an important role in Enumerative Geometry and shed new light upon classical questions in Geometry. Moreover, Gromov-Witten invariants are the central objects of my research. In my Master Thesis I try to carry over recursion formulas for classical Gromov-Witten invariants to the case of their tropical counterparts.
Maybe some day, I might combine my research interest with my interests in completely different fields. As besides my research in pure mathematics I am interested in various areas throughout the sciences. So far, I already worked on projects including fields like Astronomy, Medical Therapy Planning or Computer-aided Drug Design. Currently, I am also involved in the paleontological “Open Dinosaur Project” as a Citizen Scientist. All this is lots of fun and I love the idea of interdisciplinary working very much, although especially in the Open Dinosaur Project I really am a lay person like everybody else. If any of the attendees of this year’s HLF is also interested in views beyond the horizons of their research fields, I would be happy to discuss this!

©FalkoGauss
Falko is a Master student in Mathematics at the University of Kaiserslautern. Currently, he is working on his thesis in Tropical Geometry under the supervision of Professor Andreas Gathmann. He received a Bachelor’s Degree with a major in Mathematics and a minor in Mechanical Engineering. Besides his research in Pure Mathematics Falko was and is involved in several projects covering a wide range of sciences.

