The internet is an interesting place. I’m often told that people are being ‘baffled’ or ‘stumped’ by ‘maths puzzles’ – despite the fact that many people find maths intimidating, or didn’t get on well with it at school, they’re still prepared to spend their leisure time being tortured by problems they can’t seem to solve. (I suspect ‘This maths puzzle is being totally ignored by Facebook’ makes for a less interesting headline.)

One such puzzle is given below – using symbols to represent some unknown numbers, can you work out the answer?

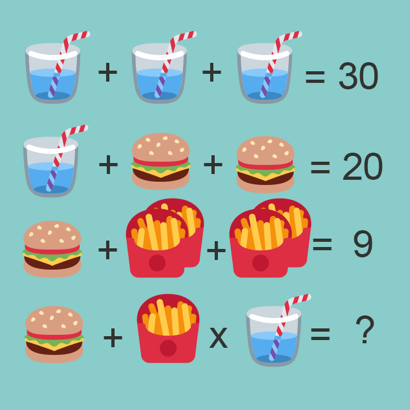
In this case the symbols are burgers, fries and drinks; the same problem has also been presented in terms of burgers, bottles of beer and glasses of beer, but any three emoji, pictures or symbols could be substituted in for them. In fact, it’s something mathematicians do all the time, except we tend to use more boring prosaic symbols like ‘x’, and ‘π’. (I guess using emoji would open up our options further – and there is already an emoji LaTeX package, for those who want to typeset it properly.)

The reason why people find these problems so ‘baffling’ is that the setters have deliberately made them so – using some tricks to nudge people towards incorrect answers, then allowing a stream of commenters to berate them when they make a mistake. One such technique is using different numbers of items in different lines. Above, the 🍟 in the third line are in pairs, whereas the fourth line has a single packet of 🍟. While it’s easy to see this when you look carefully, you might not notice it on a quick scan of the image.

Another trick is combining operations without specifying the order – for example, the fourth line above reads “🍔 + 🍟 × 🥤= ?”. But does this mean you add the 🍔 and 🍟, then multiply by 🥤, or do you multiply 🍟 by 🥤 then add 🍔? In processing a sequence of operations like this, the natural thing might be to work from left to right, processing each command one at a time: start with a 🍔, add 🍟, then multiply by 🥤. But in school we learn that operations have a standard order, and if you’ve heard the word BODMAS, or BEDMAS, you’ll know that multiplication (M) comes before addition (A), and should be resolved first.

The thing is, the way the problem is written seems to deliberately be trying to trip you up. The setter could have written “🍟 × 🥤+ 🍔= ?”, which wouldn’t have been quite so difficult to parse. Or, they could have done the proper mathematical thing, and used brackets:  “🍔 + ( 🍟 × 🥤) = ?” Most people working properly in mathematics will tell you that BODMAS is irrelevant, because you can always use brackets to disambiguate.

The worst culprits are those who do even tricksier things to confuse you. The example below, shared as a problem given to Chinese school children which subsequently ‘stumped the internet’, includes a picture of a cat – and if you look closely you’ll see the cat sometimes is wearing a whistle, and other times isn’t. The whistle is one of the unknowns in the puzzle, so ‘cat with whistle’ has a different value to ‘cat without whistle’. Most people won’t spot this on first glance, meaning they’ll get the wrong answer even if their maths is flawless.

This kind of manipulation is wasting people’s time at best, and actively unhelpful at worst – given people are already predisposed to fear maths, giving them what looks like a simple problem, then exposing them to the cruelty of social media comments sections when they get the wrong answer is surely only going to make them feel even worse about it. This blog post from 2017, by a maths teacher and education professor, shares some more detailed thoughts on the phenomenon.

That said, it’s a good sign that people are prepared to have a go at a maths thing they see on Facebook – they might enjoy the tiny buzz of solving the puzzle, and appreciate a chance to flex their maths muscles. It’s also been noted by educators that using pictorial symbols or emoji instead of algebraic variables increases many students’ ability to understand and solve this kind of problem – the website solvemoji.com has hundreds of such problems, free for educators to use.

Also, students can apparently tackle much more difficult problems in this form than they would be prepared to in a traditional setting. The examples pictured above are both systems in three variables – much more complex than many school children would usually be expected to solve.

When mathematicians are faced with systems of equations like this – called simultaneous equations – they can be categorised and understood pretty well. If all the operations are addition or subtraction, or multiplying a variable by a number, the equations are called linear.

For example, “🐶+ ☕☕ = 🍭🍭🍭🍭🍭”, also known as “🐶+ 2 ☕ = 5 🍭” is a linear equation, as the only multiplying that happens is between an emoji and a constant number (not a variable that we need to find the value of).

Linear equations behave in a nice predictable way – if all the equations in a system are linear, and you have 3 variables to find, you will need at least 3 equations that relate the variables to each other in order to find a single solution. For example, using only the second equation in the fast food example at the start, we couldn’t say for sure what either of the values are, but if we combine it with the other equations we can fix the values. In general, the number of equations relating the variables needs to be greater than or equal to the number of variables.

However, linear equations aren’t the whole story, and in the fast food and whistle cat examples above, there’s an extra complication introduced in the last line. When you multiply a cat by a whistle, or a 🍟by a 🥤, the equation becomes nonlinear – these are polynomial equations. In this case, the same number of equations as variables might not be enough to fix a single answer – for example, 🍟× 🍟= 4 has both 🍟= 2 and 🍟= -2 as a solution. If you have a mixture of linear and nonlinear equations, you can try solving the linear ones first and then substitute in the number values to make the nonlinear ones a bit easier.

One interesting point to consider here is that in these problems imply a secret additional set of restrictions on the answers, without actually saying it. In the previous paragraph, I casually mentioned the idea of 🍟= -2, but many people approaching this problem wouldn’t consider the possibility of the symbols representing anything other than a positive whole number. While 🍭= ½ is strictly possible, what if we ruled it out?

In the case where you’re only interested in whole number solutions, equations and systems of simultaneous equations like these take on a new name. Called Diophantine equations, and named after the 3rd century Greek mathematician Diophantus of Alexandria, they require the solutions to be integers (whole numbers). Diophantus was one of the first mathematicians to introduce the idea of symbolism into algebra, and only a few short millennia have taken us from there to🥤+ 🍔+ 🍔= 20.

Diophantine equations are slightly more restricted in their possible solutions than general equations – for example, if I told you that I had two different numbers that added to 3, you’d be able to find infinitely many sets of solutions – say, n, which can be any value (except 1.5, as the numbers must be different), and 3-n. But if I tell you they’re both whole numbers (and I require them to be positive), you can immediately tell me the answers are 1 and 2.

This type of equation also allows for interesting methods of attack. With a single equation in two variables, you can use the Euclidean algorithm, first finding the factors in common between the coefficients given and then working backwards to determine what combinations will give you a valid answer in whole numbers.

Other types of maths problem sometimes also turn out to be based on Diophantine equations. If you’ve ever encountered the classic water-jug-pouring type problems, where you have set sizes of containers and need to end up with an exact amount of water in one of them, that isn’t a whole multiple of one of the container sizes, this is actually a Diophantine equation.

For example, if you have one container that holds 3 litres and one that holds 5 litres, it’s possible to measure out 4 litres – and you’ll do this effectively by adding or subtracting full jugs of 3 and 5 litres. So the problem can be formulated as 3x + 5y = 4, where x and y will be positive (or negative) whole numbers representing the aggregate number of times each jug is filled or emptied. For the most elegant (if slightly sweary) solution to this particular problem, I direct you to the work of my fellow mathematicians Bruce Willis and Samuel L Jackson in one scene from Die Hard 3.