The maths behind the Fields Medal
BLOG: Heidelberg Laureate Forum

One of the prizes celebrated annually at the Heidelberg Laureate Forum is the Fields Medal – one of the highest honours a mathematician can receive, and awarded once every four years to up to four mathematicians. The award itself consists of a $15,000 prize (Canadian dollars, as it was established by Canadian mathematician Charles Fields) and an actual physical medal.
The front of the medal contains an image of Archimedes, along with the quotation “TRANSIRE SUUM PECTUS MUNDOQUE POTIRI” (“To transcend one’s human limitations and master the universe”). The back of the medal has another inscription, “CONGREGATI EX TOTO ORBE MATHEMATICI OB SCRIPTA INSIGNIA TRIBUERE”, which translates as “The mathematicians having congregated from the whole world awarded [this medal] because of outstanding writings.”
Behind this inscription is pictured an olive branch, and some lines and shapes. This design was chosen as it illustrates one of Archimedes’ favourite mathematical results – he was so proud of it, he asked for this design to be engraved on his tombstone. But what does it mean?
On the Sphere and Cylinder
A version of the diagram without an inscription in front of it is shown below, next to a 3D rendering of what it’s trying to represent – it’s a sphere sitting inside a cylinder of the same height and radius.
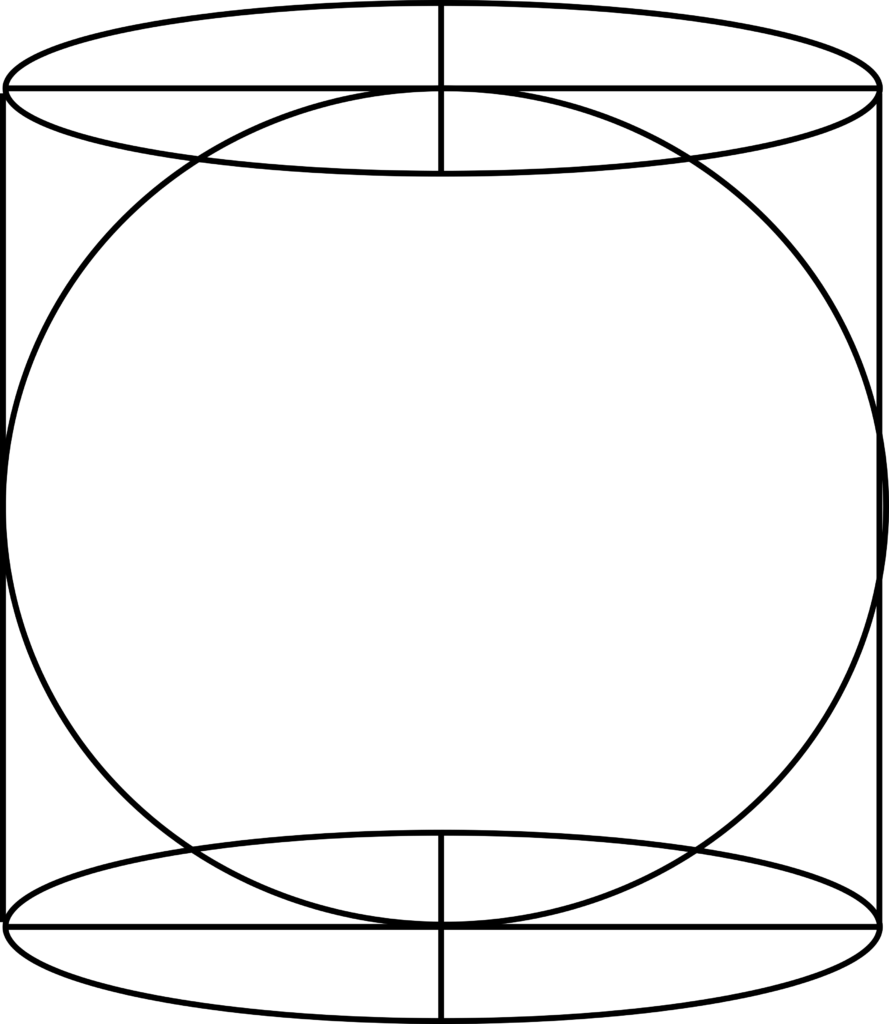

Image CC BY-SA by Pbroks13 on Wikipedia
You might be familiar with the formulae for the circumference and area of a circle – if the radius of a circle is denoted by r, we have that the circumference is 2πr, and the area of a circle is πr2. These formulae are known to all school students everywhere, and form a fundamental part of our understanding of the geometry of circles.
Archimedes went one step (and one dimension) further, and wanted to know the formulae for the surface area, and the volume, of shapes based on circles, like spheres and cylinders, and how they relate to each other. In his work “On the Sphere and Cylinder,” published in 225 BC, Archimedes gave a variety of results, including ones about how to find the surface area and volume of a cylinder and a sphere.
The formulae for a cylinder are easy enough. The outer surface of the cylinder consists of two circles (each with area πr2) and a curved surface whose height is the height of the cylinder, and which wraps around the whole circle – so its area will be the circumference of the circle times the height of the cylinder, or 2πrh (where h is the height of the cylinder). So the total surface area is 2πr2 + 2πrh, or 2πr(r + h).
The volume of the cylinder is similarly easy to work out – if you consider it as a circular prism, made by pushing a circle along a line and including all the space the circle passes through as part of the shape, it’s simply the area of the circle (πr2) times the height of the cylinder, so the formula is πr2h. If your cylinder happens to be the same height as it is wide, its height will be 2r, and so this formula would become 2πr3.
Getting a round in
For the sphere, things get a bit harder to visualise. Archimedes proved that the surface area of a sphere is four times the area of a circle found by cutting the sphere exactly in half (known as a Great Circle of the sphere). This means if the radius of the sphere is r, the surface area is 4πr2. Such a neat result!
Now the challenge is to convince yourself it’s true. One way to imagine the surface area of a sphere is to imagine a circle that’s pivoted about its diameter, and rotate the circle fully around – the edge of the circle will sweep out the surface of the sphere. (If you’re struggling to imagine this, spin your Fields Medal on the table).

If we wanted to simplify this, we could reduce the rotating circle to a rotating polygon – imagine it’s, say, a 10-sided shape (decagon), sweeping out the same circle. Since polygons with increasing numbers of sides get closer and closer to an actual circle, this is a simpler version of the problem, made up of straight edges.
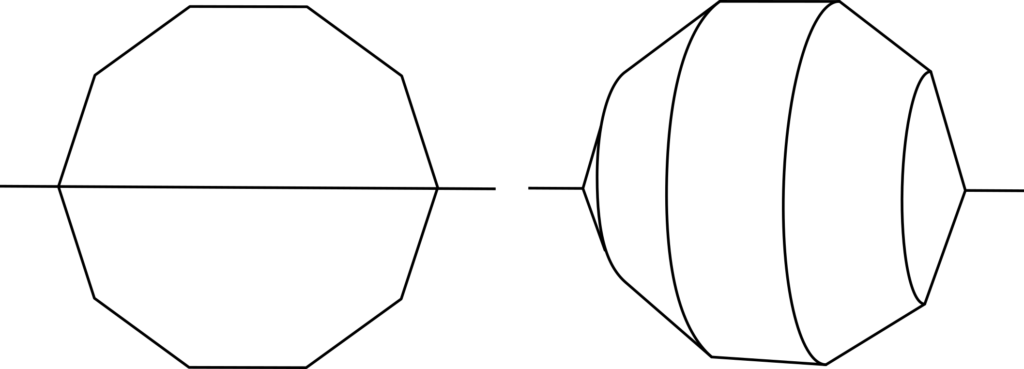
Rotating the decagon would produce an approximation to a sphere, made up of sections of cones and cylinders, each of which has a known formula for its area. From this you can get a formula for the surface area of the total shape, and if you repeat for other numbers of sides, you eventually reach a formula that depends on the number of sides the shape has – and as you increase the number of sides, this gets closer and closer to a total surface area of 4πr2.
This mirrors a more modern approach to mathematical problem-solving – in the time of Archimedes, calculus was a distant dream, but it’s based on the idea of limits – letting a value increase until it’s effectively infinite, and seeing what the result gets closer and closer to. It’s also possible to derive the volume formula using modern calculus techniques, but Archimedes would presumably have been able to intuit the limit, even if he didn’t have a word for it.
This method is often given as Archimedes’ formal derivation of the proof, but it’s also suggested that he might have originally noticed this relationship by merely comparing the volumes of cylinders and their inscribed spheres, using physical methods.

Archimedes was, after all famous for jumping out of a bathtub (having realised you could measure volume by water displacement), so he must have had some tricks up his toga sleeve for finding the volume of odd shapes. A parchment discovered in the 20th century describes a method of determining volume, attributed to Archimedes, involving balances and centres of mass.
The result Archimedes was most pleased with, and the reason it was carved on his tomb, is that of the volume of a sphere. You might have learned by heart that the volume of a sphere is given by 4/3πr3 – but if you compare this with the volume of a cylinder which has the same radius and height as the sphere – one it would fit exactly inside – you might notice that these formulae are very similar, and differ only by a factor of ⅔. Even if you didn’t notice this pleasing fact, Archimedes certainly did, and he was correct to be proud of it.
It’s fitting that the Fields Medal, a celebration of the pinnacle of mathematical achievement, contains this beautiful example of a mathematical result so important and groundbreaking for its time. A result so simple it’s now used in high-school geometry classes was, in 225 BC, actually itself worthy of a Fields Medal (if such a thing had existed then). I bet today’s Fields Medalists wish they could win the award by proving a result this simple!

