Thanks to the eponymous film, “the imitation game” is a phrase known by many people. I must confess though, before the talk by Avi Widgerson (Nevanlinna and Abel Prize recipient), on day two of the Heidelberg Laureate Forum, I wouldn’t have been able to tell you what an imitation game actually was. I might have mumbled something about computers, or even blurted out the words “Turing test”, but beyond that I would have been clueless. I learned over the course of that hour how imitation games are a tool with uses far beyond computing.

I shall begin as Widgerson did, and indeed as Turing himself did. With the Turing test.

I’m not a robot

The Turing test was posed in Alan Turing’s 1950 paper “Computing Machinery and Intelligence”. Perhaps unsurprisingly, the name “Turing test” came about later. The name Turing gave his test was “the imitation game”, providing a small indication of what the test involves.

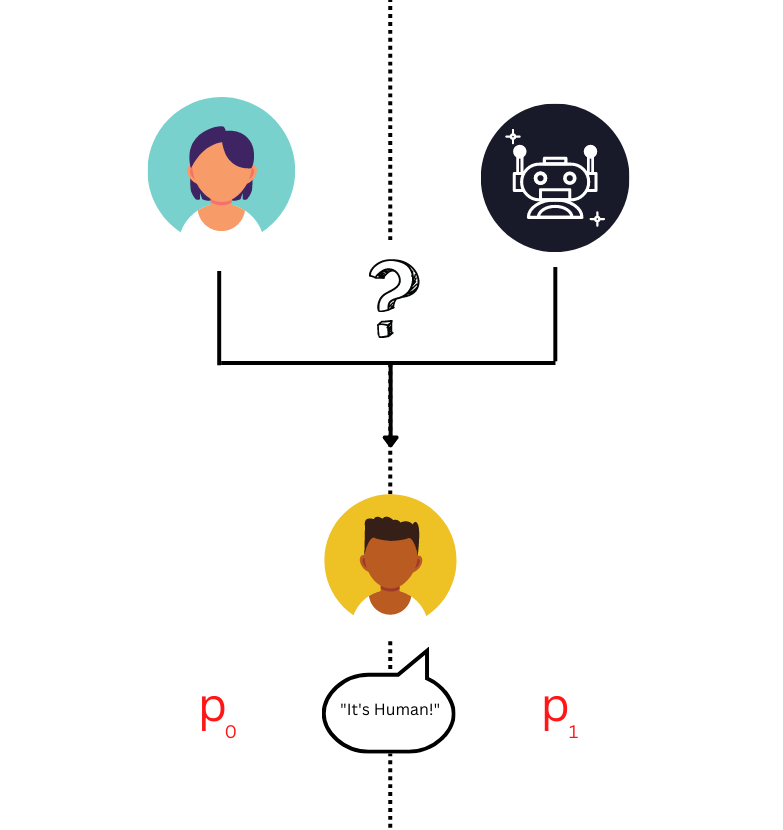
The purpose of the test is to determine whether or not a machine is able to exhibit intelligence. Put another way: can a robot think?

In the Turing test, a human referee interacts with an entity. The referee does not know whether the entity is itself human or not. At the end of the interaction, the referee must make a judgement as to the entity’s humanity. The robot entity is defined to be intelligent if a similar guess is made by every referee as it is in the case of a human entity.

Put more formally, consider a robot 🤖. Let \( p_0 \) be the probability that a referee judges a human entity to be human, and let \( p_1 \) be the probability that a referee judges the robot entity 🤖 to be human. The robot 🤖 is intelligent if for every human referee, \( p_0 \approx p_1 \).

At this point, I should say that if “intelligence” meant the same thing as it does in everyday parlance, then we would have to have a serious debate over whether or not humans are the right benchmark to be using. Intelligence here is defined as the ability to pass this test. That is precisely of the beauty of the test. It circumvents the philosophical debate over what it means to think, and focusses instead on the behavioural viewpoint.

The use of imitation games doesn’t stop at the Turing test though, and neither did Avi Widgerson’s talk. The imitation game can be treated as a framework and applied in many diverse scenarios.

In this paradigm, two things are considered to be the same if they cannot be distinguished by a reasonable test. It’s clear to see that this can have many different applications, and Widgerson introduced four of these in his lecture, from fields across mathematics and computer science.

Lock and Key

It is not uncommon to hear conversations about encryption at the Heidelberg Laureate Forum. Indeed, we were treated to a panel on post-quantum cryptography on the Friday of the forum.

In discussing how we protect our messages, one facet that is often overlooked, though, is what it actually means for an encryption algorithm to be “secure”, and how we can message that.

The initial instinct is often to say that an algorithm is secure if it is impossible for anyone but the intended recipient to decrypt a message that was encrypted using that algorithm. But this begs the question, how do we know that it’s impossible? What if a decryption method exists but just hasn’t been found yet?

A good measure for how secure an encryption algorithm (let’s call it Enc) is, is whether or not two messages encrypted with it are distinguishable. If an encrypted message can’t be distinguished from random noise without the decryption key, it means that the encryption leaves no information about the initial message readable to the outside observer.

Now it’s time for another imitation game.

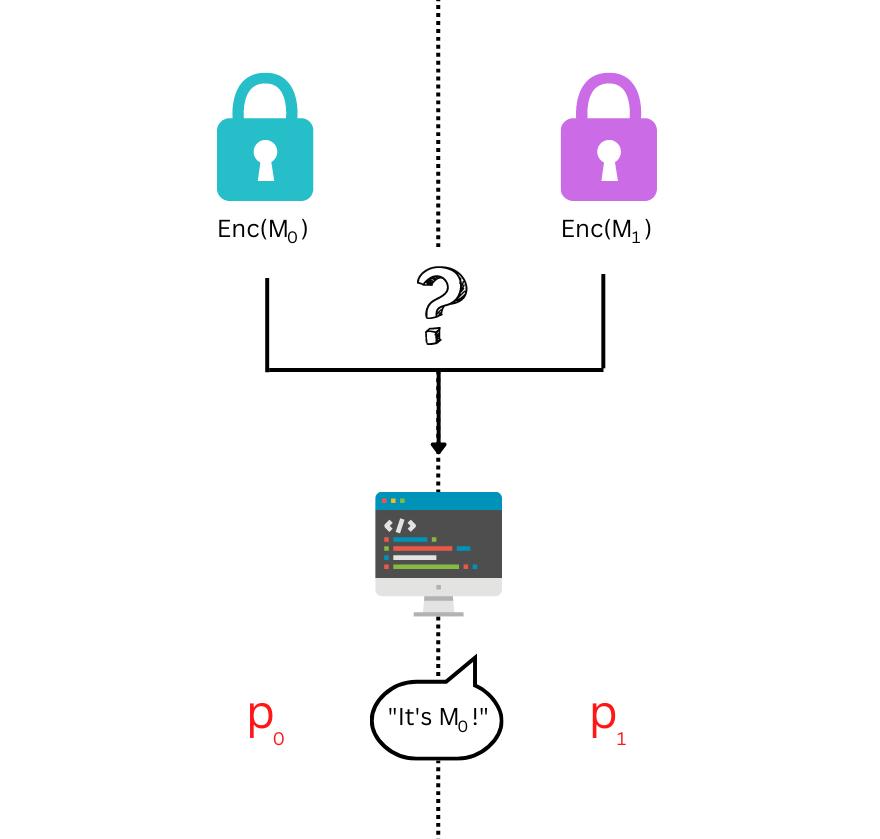
Instead of comparing a human and a robot, this imitation game compares two messages \( m_0 \) and \( m_1 \). We encrypt both of our messages using the encryption algorithm, Enc. Instead of a human judge, we have an “efficient algorithm” referee, who is tasked to determine whether the message it receives was originally \( m_0 \) or \( m_1\).

Let \(p_0\) be the probability that the referee judges Enc(\( m_0 \)) to be \( m_0 \), and let \( p_1 \) be the probability that the referee judges Enc(\( m_1 \)) to be \(m_0\). The encryption is secure if for every efficient-algorithm referee \(p_0 \approx p_1\).

Does this sound familiar? It should! This is analogous to the Turing test. We haven’t even scratched the surface of what imitation games can be used for though.

Security and privacy go hand in hand, so it’s perhaps unsurprising that Widgerson also discussed how imitation games can be used to assess privacy.

The specific situation Widgerson posed was the dilemma posed by databases. From data we’ve voluntarily given in surveys, to data submitted in censuses, to data that has been collected without us knowing, our data is stored in databases worldwide. In order for the data to be useful it needs to be detailed, but the more detailed it is, the more identifiable. A natural question arises: How can we verify that individuals can’t be identified from the data?

In their 2006 paper, Dwork, McSherry, Nissim and Smith proposed using an imitation game. We compare two databases \(D_0\) and \(D_1\), which are “adjacent”. This means that there is precisely one entry different, in this case \(D_0\) includes Jane Doe, but \(D_1\) does not . The referee in this case is any database query \(Q\). A filter is applied to the databases and the filter is said to be differentially private if for every adjacent \(D_0\) and \(D_1\), and every legal query \(Q\), \(p_0 \approx p_1\).

Once again, the imitation game gives us a definition, based very much in the real world. In this instance, we get a definition of the word “private” and it’s a sensible one. If no query can detect that Jane Doe is in the database, then Jane has no need to worry. In a practical sense at least, the filter is private.

“I’m so random”

You may have started to see the pattern by now, and I have one final example to share. This concerns randomness.

Randomness is much like artificial intelligence in that there are many philosophical debates as to whether it truly exists. Some argue that humans cannot simulate randomness (in fact, this was a discussion I had with some other members of the press at the Heidelberg Laureate Forum!). Putting human ability aside, many debate whether, say, a coin flip truly is random because the result is entirely determined by the initial conditions and the toss.

But beyond this debate, it’s important to consider how randomness can be simulated. Regardless of whether or not a coin toss is genuinely random, it’s just impractical to flip a coin every time you need a generate a random number. Suppose, then, that we want a pseudo-random source. What would this look like? How do we define “pseudo-random”? Is the stock market, or rainfall sufficiently random?

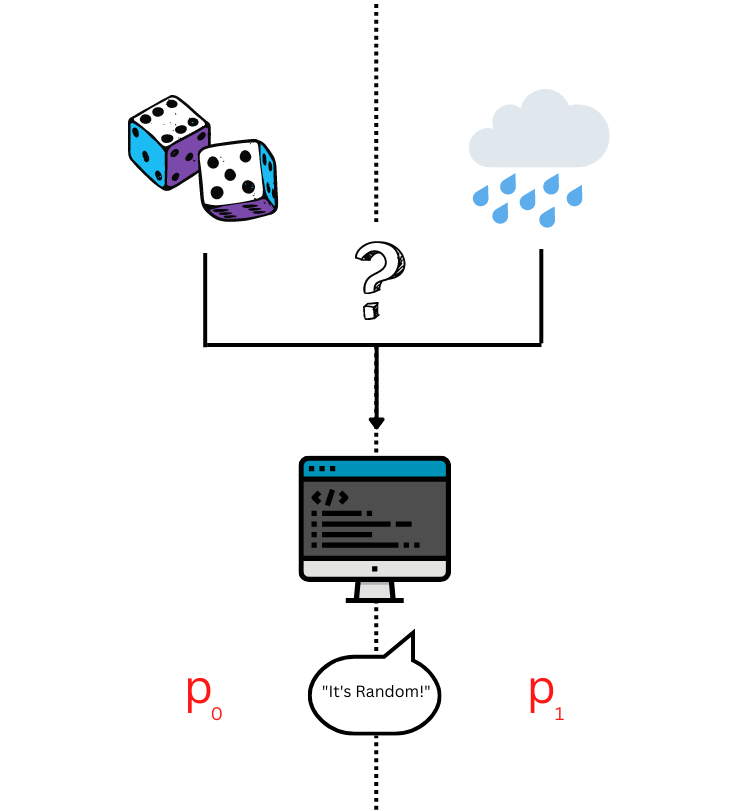
Once again, imitation games come to the rescue in answering these questions, in a method first suggested by Blum and Micali in 1981, and Yao in 1982.

We set up this imitation game with a random input, and our potential pseudo-random input. We give one of these inputs to an algorithm \(A\) (our referee), which is tasked in determining which of the two inputs it is. As before, \(p_0\) is the probability that the algorithm \(A\) judges the random input correctly to be the random, and \(p_1\) is the probability that the algorithm \(A\) judges the potentially pseudo-random input to be the random input. The source is pseudo-random if for every algorithm referee \(p_0 \approx p_1\).

The examples are endless…

These STILL aren’t all the examples of imitation games that Avi Widgerson gave, but I shall stop here.

Throughout the course of his talk, Widgerson gave a whistle-stop tour of mathematics and computer science through imitation games. Turing was famously a polymath and it’s fitting that his idea is proving important across so much of science.

Avi Wigderson’s talk, as well as the entire scientific program of the 9th HLF, can be viewed on the HLFF YouTube channel.