The Fields Medal in Statistics
BLOG: Heidelberg Laureate Forum

One of the prizes whose laureates are regulars at the HLF is the Fields Medal – awarded by the International Mathematical Union (IMU) every four years since 1950, and celebrating the very pinnacle of mathematical achievement. This year, four prizes were awarded to four more top mathematicians in recognition of their outstanding work in research and potential for future achievement.
Winners of the Fields medal are selected to represent “a diversity of mathematical fields”, although one branch of mathematics is notably absent from the prize listing – statistics. While there have been some awards to statistical physicists, and several for work in probability theory, the word ‘statistics’ is otherwise completely absent from the historical list of winners.
Since statistics is an important and scientifically vital branch of mathematics, it seems a shame it has been overlooked so long. I thought I would try to make up for this by applying some real (serious, important) statistical analysis to the facts and figures behind the Fields Medal and its decades-long history.
Fields Until You’re 40
One of the most contentious aspects of the medal is the requirement for winners to be under 40 at the time of receiving the award – partly to ensure the ‘potential for future achievement’ aspect of the award has some time to develop, but possibly discouraging to mathematicians facing the prospect of growing too old to win a Fields Medal.
It is certainly true that mathematical brilliance can occur at any age, and putting pressure on people to make big discoveries and achievements early in their career can be unhelpful, especially to those with other commitments or restrictions on their work time. It is also good to celebrate the achievements of youth – but given this is the leading prize in the field (the ‘Nobel Prize’ of mathematics), some argue it should be possible to receive the same amount of recognition even if you didn’t quite get there until after your 40th.
In this spirit, the first bit of statistical analysis I attempted was to look at the ages of prize winners at the time of winning the award. As you might expect, most are quite close to the 40-year-old cutoff, but since the start of the award (two prizes were awarded in 1936, but then the every-four-years pattern was established in 1950) there has been a general creep upwards in age, shown on the plot below. Each winner is represented by a small golden disc (like a Fields medal).
The youngest Fields Medalist ever was Jean-Pierre Serre, who won in 1954 at the sprightly age of 28 for achieving major results on the homotopy groups of spheres and spectral sequences, and for reformulating results from complex variable theory in terms of sheaves. The first 40-year-old to win was Jean Bourgain, as late as 1994, and it turns out he was also the oldest winner to date, being exactly 40 years 5 months 6 days at the time of the award’s presentation (for work in mathematical analysis, including the geometry of Banach spaces, convexity in high dimensions, harmonic analysis, ergodic theory, and nonlinear partial differential equations from mathematical physics).
Field(s)work
The amount of information available about Fields Medalists (partly due to a helpfully thorough Wikipedia page on the award, and partly through the ICM’s own website and some other diligent Googling) means it’s also possible to determine some stats about their careers. For instance, around 45.3% of Fields Medalists still work (at least partly) at the same institution they worked at when they received the award, or did when they retired, while 82.8% stayed in the same country but at a different institution.
7 of the 64 Fields Medalists were also recipients of the Abel Prize, and only 5 have the glorious trifecta of a Fields Medal, Abel Prize and the Wolf Prize in Mathematics (awarded by the Wolf Foundation in Israel). Similar to the EGOT (Emmy, Grammy, Oscar and Tony), an honour held only by 17 Hollywood stars, I have decided to call this the WAF and hold it in similar regard.
Given that each Fields Medal is awarded for specific mathematical contributions, a little data-crunching lets us find common words and phrases within the prize announcements to see which areas of maths the Fields Medal is being awarded for (subject to some minor issues about wording sometimes not being reflective of the actual topic being talked about, which means this is a crude measure) and find out what’s popular.
As discussed above, none mention statistics (except in the context of statistical physics), and only 3 use the word ‘probability’; big hitters include ‘differential equations’ (8 winners), ‘topology’ (9 winners) and ‘number’ (10 winners, with ‘number theory’ contributing 6). It looks like pure maths wins, with ‘geometry’ getting a whopping 18 mentions.
Nationalities
It’s also possible to determine, through some compilation of demographics and population statistics, which country has contributed the most Fields Medalists to the world. Some countries are definitely well-represented on the list – 18 winners have been from America or had partly American heritage, 13 from France, 9 Russian, and 8 British.
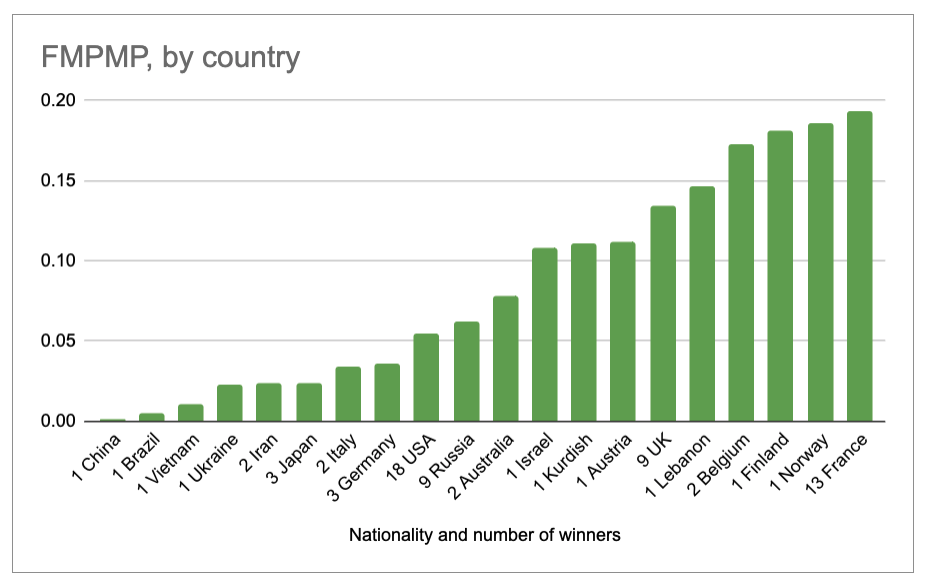
But considering that some of these countries are drawing from a larger population, we can determine that the top country for producing Fields Medalists is New Zealand. With only one winner (Vaughan Jones, in 1990) and a population of 5.084 million, they have the most per capita of any country in the world.
From this we can derive a unit of measurement – for every 1 million people in New Zealand, 0.197 of them are Fields Medalists. Close second is France with 0.193 FMPMP (Fields Medalists Per Million People), then Norway at 0.186 FMPMP. Despite their impressive total, the USA has a mere 0.055 FMPMP, while China (with one winner, Shing-Tung Yau who’s Chinese-American) has a mere 0.0007 FMPMP.
One might start to use such statistics to make inferences about what it takes to be a fields medalist – for example, it looks from the data like being male (only 2 female winners so far) and from the global north will be good moves to make if you’d like to win one; it also looks like almost 60% of Fields Medalists have between 12 and 15 letters in their full name, so that might also be good to shoot for. (The longest name prize goes to Alexander Grothendieck, checking in at 21 letters – a true giant of mathematics.)
Real Statistics
Obviously, this isn’t how statistical analysis works (and you may have already noted that so far I haven’t done much analysis, but merely collected and presented statistical information, which is much easier). I’m not a statistician, so my hopes of making any insightful claims are slight. But much of the data I’ve presented is meaningless outside of a wider context.
For example, the property of having 12-15 letters in your name is something that applies to a large number of people in the world. A meaningful (if slightly pointless) statistical analysis might involve determining the distribution of name lengths across the entire population of the world, and considering whether the proportion of 12-15ers in the whole population is lower or higher than in this small subset of Fields Medalists – this would tell us whether the length of your name has any bearing on the likelihood of winning.
If the value is found to be more or less than the wider statistic, it might then be worth considering whether it’s significantly different. As well as the proportion of people in the 12-15 letter range you can study the distribution of name lengths of the whole set (see below), and compare this to the general population.
If you took any random sample of 64 people, you wouldn’t expect their average name length, or the distribution more generally, to be the same as that of the whole population. But you could work out, if you took lots of 64-person samples, how the average value varies between the different samples. You can then compare the average for the Fields medalists to the averages for these randomly selected samples, and see if it’s similar – or an outlier.
Typically, if only one in 20 random samples has an average as extreme as the average value of your set, this is considered to be statistically significant – the data you’re observing varies enough from what you’d normally expect that this is a meaningful observation, which might mean there’s a correlation between being good at maths and having names of a particular length – there probably isn’t.
This is the power of statistics – it’s not just about seeing differences, but about understanding what you’d expect and whether your observation differs from that.
Another aspect to consider is whether this correlation is meaningful at all – it might be that if Name Length and Medal Likelihood do increase together, this is due to a third factor (maybe people with long-ish names have more patience because it takes so long to spell their name, and therefore perform better in mathematical research roles). Or there could be other cultural or environmental factors that influence both at the same time.
Most statisticians, however, would immediately reject conclusions based on such a small data set (n=64). I guess the only answer is for us to keep awarding the Fields Medal every four years, and hope that it helps to uncover new talent by recognising some world-class statisticians who can continue this important work. Or, we could look at the winners of some of the top statistics prizes, like the COPSS Presidents’ Award and the International Prize in Statistics.


France has the most field medalist, and that’s no surprise, because France has a long history of excellence in mathematics. Just think of Pascal, Descartes, the Bourbaki Group, Grothendieck, Connes, Villani or the mathematical institutes CIRM, IHES and IHP.
On the other hand, there is no country in the world where really many mathematicians do research. And it is even unclear which work areas are the most important in mathematics.
In physics, this question can be answered clearly: quantum and gravitational theories are the most important branches in basic physics and optics and acoustics, physics of condensed matter, electromagnetism and photonics, mechanics and thermodynamics have the most applications.
Of course, there are also well-known mathematical branches such as algebra, geometry, trigonometry, calculus, statistics and probability, but most of these areas are no longer the subject of mathematical research.
If you search the Internet for what the top 10 mathematicians are researching today, then you will be lost because of the diversity of their research interests and because even most mathematicians do not know what they are doing.
Terence Tao’s main interests are, for example: Green Tao theorem, Erdő’s discrepancy problem, compressed detection, Tao’s inequality, analysis, oscillatory integrals.
Andrew Wiles explores the Taniyama-Shimura presumption for semi-stable elliptical curves, Fermat’s last movement, Iwasawa theory.
Perhaps mathematics is an area in search of research topics.