Perfect Squares

Squares – shapes with four right-angle corners, and four equal-length sides – are lovely. Mathematicians especially love them, as evidenced by the number of nice geometrical and numerical constructions based on squares. For example, a square number is one which is made by multiplying a number by itself – and the resulting number, if it were a number of beads, could be laid out in a square grid.

As well as squaring numbers, some mathematicians also like to square shapes. Squaring a shape involves dividing it up exactly into squares with whole number (integer) length sides. For example, if I have a 10 by 20 rectangle, I could split it up into two squares of size 10 by 10.

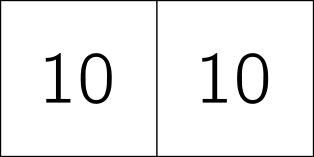
This is pretty simple – but squarings of a shape (ways of covering it by integer-sized squares) can get more complicated. This is a 15-by-25 rectangle covered using squares of size 15, 10, 5 and 5.

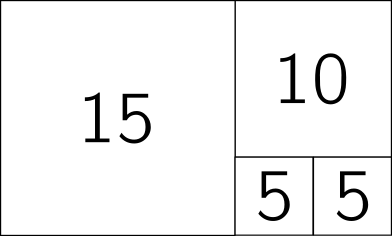
Boxing Yourself In

For some shapes, this is easy to do, and for others it’s impossible. We can make it into a harder puzzle by adding some extra constraints. For example, a squaring is called simple if it has no subset of two or more squares that themselves form a square or rectangle. If such a subset does exist, the squaring is called compound.

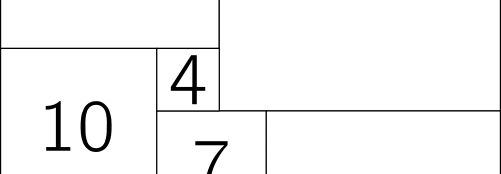
For example, the squaring above using 15, 10, 5 and 5 can be split to the right of the 15 square, giving two separate pieces that are themselves rectangles. Or I could just break off the two 5s to get a rectangle. If no rectangular piece made of two or more squares can be sectioned off in this way, the squaring is simple. 

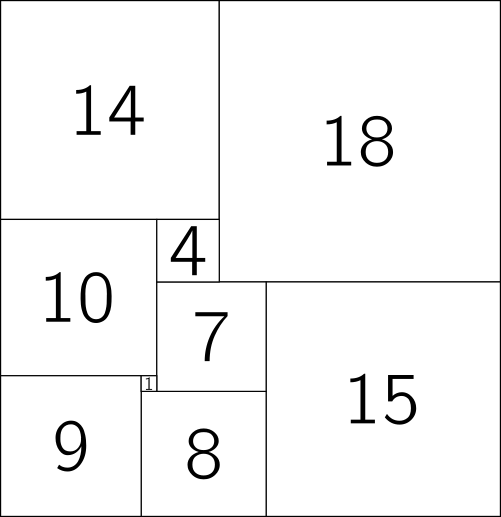
Here’s a simple squaring of a 15 by 11 rectangle, using squares of size 6, 6, 5, 5, 4, 4, 3, 1 and 1:

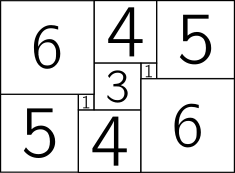
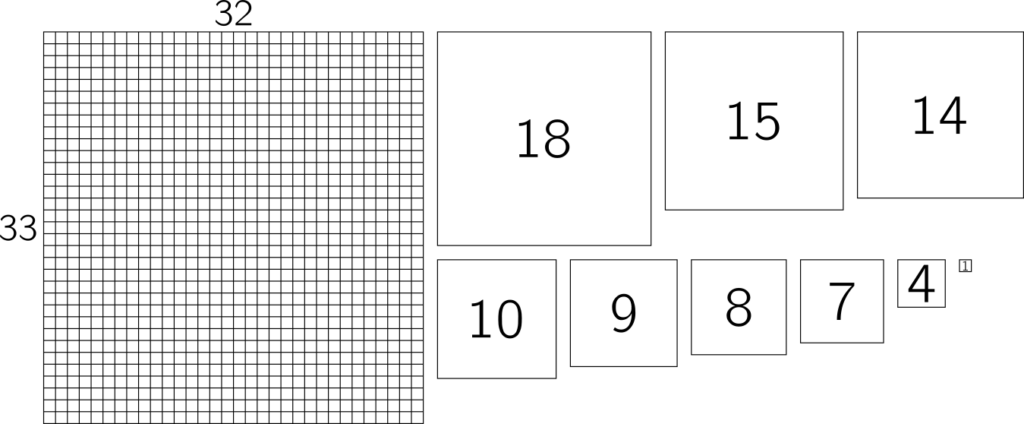
If we want to ramp up the difficulty, we could require a squaring to be perfect – that is, each of the individual squares making it up needs to be a different size. Such squarings are difficult to find, and it’s a nice puzzle to fit the pieces together. Below is a 33 by 32 rectangle, which has a simple, perfect squaring using squares of size 18, 15, 14, 10, 9, 8, 7, 4 and 1. Can you fit them together to fill the square? One solution is at the bottom of the post.

While squaring rectangles might be fun, it’s still not the most difficult this problem gets. Hardcore squarers are looking to square the ultimate prize: a square.

Perfectly Squaring the Square

Dividing up an integer-sized square into distinct integer-sized squares is no mean feat. Squarings of squares and rectangles have been studied since as long ago as 1903, and perfect squarings of squares were first seriously attempted by a group of Cambridge mathematicians in the 1930s. In 1939 the first perfect squared square was published – made up of 55 squares, and measuring 4205 along each side (but sadly a compound squaring). It’s pretty impressive, given that at the time, there were no computers to run searches – these early squares were discovered by hand.

As time progressed and technology caught up with squarers’ ambitions, it was possible to find and confirm the smallest possible perfect squared squares using computer programs. The fewest possible squares a perfect squared square can be squared with is 21, and such a squaring was found in 1978 by A. J. W. Duijvestijn. It measures 112 along each side, and is now used as the logo for the maths society at Trinity College, Cambridge.

However, it’s not the actual smallest a squared square can be – that honour is held by three different squares, each comprising 22 squares and measuring 110 along the side. These were proven to be the smallest such squares in 1999. One is shown here.

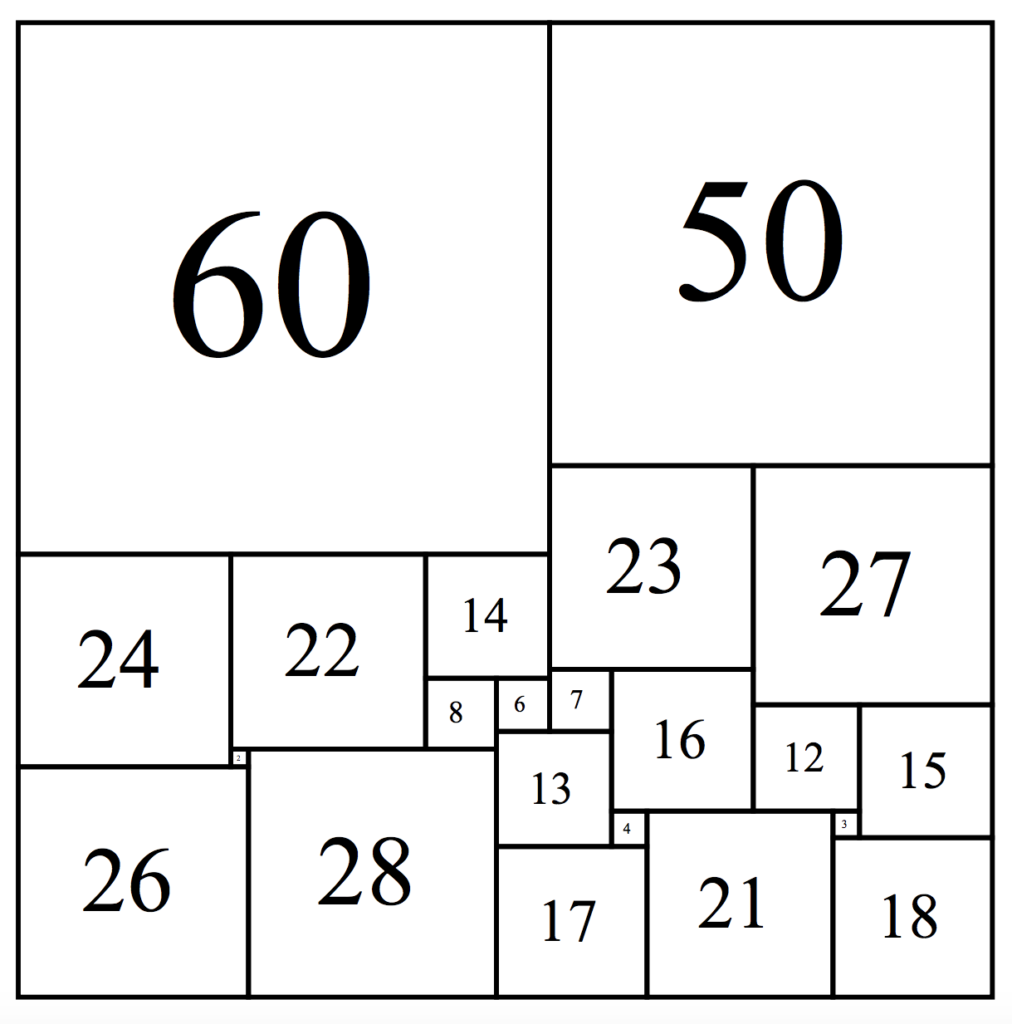
Even the simplest perfect squared squares are sufficiently unwieldy that they probably aren’t easy to work out by hand, and this problem has benefitted hugely from the application of computer programmes. Mathematicians continue to find new ways to constrain the problem – could we find a perfect squared square with a square positioned exactly symmetrically in the centre? Can we place other constraints on the relative sizes of the squares? What about cubing the cube? The possibilities are endless (and outlined in detail, of course, in an online catalogue at squaring.net). 

One of my favourite things about simple perfect squared squares is that they’re so aesthetically pleasing. They don’t have any fault lines or subsections you can easily take out, and the squares jostle together in a way that shouldn’t work, but somehow just exactly does. This might be the reason why they’re used for artworks and decoration – the images below show an inlaid wooden table top, a stained glass window, and a set of coasters, all employing squared square designs.

And finally, here’s the solution to the puzzle above (rotations and reflections of this also work!):