Nichtlineare Wellen und Solitonen
BLOG: Heidelberg Laureate Forum

Es ist Zeit, die Zusage aus meinem letzten Beitrag einzulösen: Wie passen ein „ordentliches“ Verhalten und Nichtlinearität zusammen?
Lineare Systeme sind die braven, überschaubaren, diejenige, deren Verhalten man (im Allgemeinen) gut vorausberechnen kann. Dagegen sind die nichtlinearen die Chaoten: Mit ihnen kann alles Mögliche passieren, und mit der Vorhersagbarkeit sieht es schlecht aus, weil die kleinste Abweichung in den Anfangsdaten das Verhalten des Systems völlig verändern kann.
Wie kann aus nichtlinearen Verhältnissen Ordnung entstehen? Zwei Möglichkeiten hatte ich aufgeführt: Entweder ist das System „fast linear“, will sagen, einem linearen System so ähnlich, dass man den Unterschied außer Acht lassen kann – zumindest für eine Weile. Das ist der Grund, warum unser Kalender jedes Jahr im Wesentlichen gleich funktioniert: Das Planetensystem ist zwar im Prinzip chaotisch, aber das macht sich erst nach ein paar Millionen Jahren ernsthaft bemerkbar.
Oder viele chaotische Ereignisse wirken in ihrer Gesamtheit wie Zufall, und das Verhalten des Gesamtsystems ist aus statistischen Gründen sehr ordentlich. Das ist das, was im Kochtopf, allgemein in thermodynamischen Systemen, passiert.
Und dann gibt es dieses merkwürdige Phänomen, das Fermi, Pasta und Ulam bei ihren Computerexperimenten entdeckten: Lauter Massenpunkte sind durch nichtlineare Federn aneinandergekoppelt. Stößt man einen von ihnen an, so breitet sich eine Welle durch die Kette aus – so weit nichts Besonderes –, aber sie zerfließt nicht. Das würde nämlich bei linearen Systemen passieren, wenn sie nicht gerade so klinisch rein sind wie elektromagnetische Wellen im Vakuum.
Wie war das? Elektromagnetische Wellen in Materie, zum Beispiel Licht in Glas, verhalten sich noch ziemlich ordentlich; eine lineare Theorie beschreibt das ganz gut. Aber die Ausbreitungsgeschwindigkeit ist nicht mehr konstant, sondern hängt von der Frequenz ab. (Da war was: Brechungsindex = Verhältnis der Ausbreitungsgeschwindigkeiten ist abhängig von der Frequenz = Farbe der Lichtwelle, deswegen kann man mit einem Prisma das Licht in seine Spektralfarben zerlegen …) Ein einzelner, lokal begrenzter Stoß wäre als Überlagerung von gewöhnlichen Wellen verschiedener Frequenzen zu beschreiben, und wegen ihrer verschiedenen Geschwindigkeiten laufen die auseinander, das heißt, die an einer Stelle konzentrierte Erregung zerfließt. Das könnte man auch bei Wasserwellen beobachten; leider sind Wasseroberflächen zweidimensional, und die kreisförmige Welle, die ein eingeworfenes Steinchen hinterlässt, nimmt schon deswegen an Höhe ab, weil ihre Energie sich auf einen immer größer werdenden Kreis verteilt; gegen diesen Effekt fällt das Zerfließen nicht groß auf.
In einem engen Kanal bewegt sich das Wasser dagegen im Wesentlichen eindimensional. Wenn die Kielwellen der Schiffe allmählich kleiner werden, ist das echtes Zerfließen (ja, Reibungseffekte spielen wie immer auch eine Rolle). Umso bemerkenswerter ist es, wenn das nicht stattfindet! Deswegen wird noch heute gerne ein Mensch namens John Scott Russell zitiert, der 1834 beobachtete, wie von einem plötzlich angehaltenen Schiff eine einsame Welle sich löste und durch den Kanal wanderte. Russell folgte ihr zu Pferde über mehrere Meilen, ohne dass sich ihre Form nennenswert änderte.
Irgendeinen Effekt muss es geben, der eine vom Zerfließen bedrohte Welle wieder aufsteilt. Es dauerte immerhin bis 1895, bis die beiden Niederländer Diederik Korteweg und Gustav de Vries die Sache in eine mathematische Gleichung fassen konnten: eine nichtlineare partielle Differenzialgleichung, die zum Beispiel so aussieht: \[{\partial u \over \partial t} = 6u {\partial u \over \partial x} + {\partial^3 u \over \partial x^3} \] \(u\) ist die Höhe des Wassers über der Gleichgewichtshöhe, abhängig vom Ort \(x\) und der Zeit \(t\), und die Maßeinheiten sind gerade so gewählt, dass alle Vorfaktoren gerade gleich 1 bzw. 6 werden. Der Term \({\partial^3 u \over \partial x^3}\) macht das Zerfließen, und \(u {\partial u \over \partial x}\) macht das Aufsteilen.
Die Anwendbarkeit der Korteweg-de-Vries-Gleichung für echte Wasserwellen in Kanälen ist eher begrenzt. Die von Scott Russell beschriebene einsame Welle ist nicht wirklich häufig zu beobachten; und in der Tat mussten Korteweg und de Vries in ihrer Veröffentlichung sehr viele Annahmen machen, die anscheinend nicht immer erfüllt sind. Die Mathematiker dagegen fahren mittlerweile total auf die Gleichung ab. Man kann nämlich über ihre Lösungen eine große Menge von Aussagen treffen – vollkommen unerwartet für eine nichtlineare Gleichung.
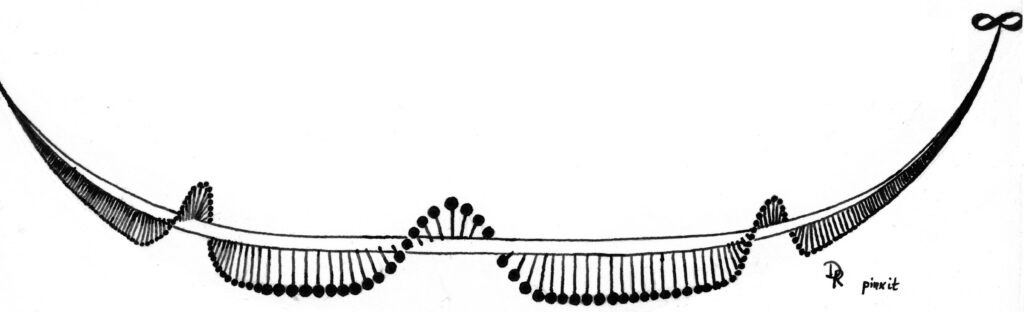
Es beginnt damit, dass es für die Gestalt der einsamen Welle eine explizite formelmäßige Darstellung gibt. Man setzt voraus, dass die Lösung der Gleichung sich in unveränderter Gestalt mit konstanter Geschwindigkeit bewegt, führt also ein mitwanderndes Koordinatensystem ein. Dann hängt die Lösung nicht mehr von der Zeit, sondern nur noch vom Ort ab, und die Gleichung vereinfacht sich zu einer gewöhnlichen Differenzialgleichung. Deren Lösung hatten schon Korteweg und de Vries gefunden. Sie hat im Wesentlichen die Form \[u(x)={1\over\cosh^2 x}= {4 \over (e^x+e^{-x})^2}\; .\] So sieht sie aus:

Es gibt sie in allen Größen. Je größer sie ist, desto steiler und zugleich schneller ist sie. Und wenn eine große einer kleinen begegnet, dann vereinigen sie sich nicht etwa, sondern die große überholt im Effekt die kleine. Hinterher sieht es, bis auf eine kleine Verschiebung, so aus, als wären sich die beiden nie begegnet.
Ein solches Verhalten beobachteten Norman Zabusky und Martin Kruskal 1965 bei Computersimulationen (seit den Zeiten von Fermi, Pasta und Ulam hatten die Geräte schon mächtig an Leistung zugelegt). Bei dem Versuch, die Ergebnisse dieser Simulationen durch eine Näherungsformel zu beschreiben, probierten sie herum – und stellten fest, dass ihre Formel eine weitere exakte Lösung der Gleichung beschrieb!
Das war nun eine echte Sensation. Wenn man zwei Lösungen einer nichtlinearen Gleichung addiert, kommt im Allgemeinen keine Lösung heraus – sonst wäre die Gleichung ja linear –, aber mit einer etwas komplizierteren Verknüpfung zweier elementarer Lösungen funktioniert das.
Wie man nun nachrechnen konnte, verhalten die beiden einsamen Wellen sich so, wie sich die theoretischen Physiker den Stoß zweier Billardkugeln vorstellen, die in ihrer Bewegungsfreiheit auf eine Gerade beschränkt sind. Von hinten kommt eine schnelle und stößt die langsamere an. Daraufhin tauschen die beiden Energie und Impuls aus, die bisher langsame läuft mit der Geschwindigkeit der bisher schnellen davon und umgekehrt.
Da sie sich also wie Teilchen verhalten und die Namen der Elementarteilchen (Proton, Neutron, Elektron …) auf „-on“ enden, wurden die einsamen Wellen („solitary waves“) kurzerhand „Solitonen“ getauft. Unter diesem Namen erlangten sie fortan eine erhebliche Berühmtheit. Sie tauchten nämlich in den verschiedensten Kontexten auf.
Der spätere Abel-Preisträger Peter D. Lax fand 1968 ein Kriterium, mit dem man bestimmen konnte, ob ein bestimmtes System Soliton-Eigenschaften aufweist. Und da fand sich so allerlei. Insbesondere gibt es ein System aus Massenpunkten und nichtlinearen Federn zwischen nächsten Nachbarn, das nicht nur ungefähr ein Soliton-System ist, sondern exakt. Nach seinem Entdecker Morikazu Toda heißt es Toda-Gitter („Toda lattice“). Und zwar ist die (abstoßende) Kraft, die eine Feder bei der Auslenkung \(\Delta x\) ausübt, proportional zu \(e^{-\Delta x}\). Sie drückt also ihre Endpunkte am intensivsten auseinander, wenn sie sehr komprimiert wird, und wird umso schlapper, je länger sie wird. Es ist etwas schwierig, sich eine physikalische Realisierung vorzustellen, selbst wenn man – was am Systemverhalten nichts ändert – zu jeder Federkraft eine Konstante addiert; aber das macht nichts. Auf jeden Fall ist das Kraftgesetz echt nichtlinear.
Ein anderes System haben sich die Quantenphysiker ausgedacht. Dass eine Welle und ein Teilchen eigentlich dasselbe sind, gehört ja zu den Grundideen der Quantenmechanik. Aber so, wie die Theorie formuliert ist, sagt die Wellenfunktion zu einem Teilchen nur, mit welcher Wahrscheinlichkeit man das Teilchen am Ort \(x\) vorfindet, wenn man nachmisst (und damit die schöne Wellenfunktion ruiniert). Eine solche Wellenfunktion kann niemals zwei miteinander interagierende Teilchen beschreiben; vielmehr benötigt die Theorie für diesen Fall neue Konstruktionen.
Wenn es aber so eine Wellenfunktion für mehrere Teilchen auf einmal gäbe, dann müsste die Gleichung, die ihre Zeitentwicklung beschreibt, nichtlinear sein, im Gegensatz zur linearen Schrödinger-Gleichung, die solches für die üblichen Wellenfunktionen tut. Eine solche Gleichung haben die Physiker tatsächlich gefunden. Ihre Gedankenspiele sind fern der Realität – wogegen nichts einzuwenden ist, man kann die Anpassung an die Realität ja nachholen, wenn man sich mit dem System etwas besser auskennt. In diesem Fall muss man vorläufig damit leben, dass der Raum nur eine Dimension hat.
So sieht die Gleichung aus: \[ {\partial^2 u \over \partial x^2}-{\partial^2 u \over \partial t^2}= \sin u \] Sie heißt „Sine-Gordon-Gleichung“ – wieder so ein Wortspiel. Es gibt eine Gleichung, die so ähnlich aussieht und nach ihren Entdeckern „Klein-Gordon-Gleichung“ genannt wird. Ersetzt man deren rechte Seite durch den Term mit dem Sinus, dann liegt die Benennung nahe, weil sich im Englischen „Klein“ auf „sine“ wie Sinus reimt.
Es gibt sogar ein mechanisches Modell, das die Sine-Gordon-Gleichung realisiert – zumindest in der Theorie. Man nehme ein unendlich langes Gummiband und spanne es waagerecht aus. In das Gummiband piekt man genau von unten lauter Stecknadeln Kopf an Kopf. Masse steckt nur in den Stecknadelköpfen, alles andere ist masselos. Das Gummiband hängt auch nicht durch; aber es ist torsionselastisch. Wenn man es in sich verdreht, wehrt es sich mit einer Rückstellkraft.
Den Zustand niedrigster Energie nimmt das System an, wenn alle Köpfe nach unten hängen. (Ja, es gibt ein konstantes Gravitationsfeld über die ganze unendliche Länge des Gummibands – ich sage doch, das Modell ist sehr theoretisch.) Aber man kann eine Kinke in das Gummiband machen, das heißt es so verdrillen, dass irgendwo die Stecknadelköpfe eine Runde um das Gummiband drehen und dann wieder brav abwärts hängen. Die Variable \(u(x)\) ist in diesem Modell der Winkel des Stecknadelkopfs an der Stelle \(x\) gegen die Ruhelage.
Diese Kinken sind die Solitonen der Sine-Gordon-Gleichung. Sie können das Gummiband entlangwandern, und wenn sie einander begegnen, tauschen sie Energie und Impuls aus wie die Massenpunkte im eindimensionalen Billard. Zu allem Überfluss gibt es rechtsgedrehte und linksgedrehte Kinken. Wer denkt da nicht an Teilchen und Antiteilchen? Allerdings: Wenn sie einander begegnen, vernichten sie sich nicht gegenseitig, sondern durchdringen einander und wandern weiter. Sonst würden Gesamtenergie und -impuls nicht erhalten bleiben.
Es gibt übrigens eine Grenzgeschwindigkeit. In den gewählten Maßeinheiten, die wieder jeden Vorfaktor verschwinden lassen, hat sie den Wert 1. Schneller als diese „Lichtgeschwindigkeit“ kann kein Soliton sich bewegen, und wenn es sich dieser Geschwindigkeit nähert, wird es zusammengedrückt – relativistische Längenkontraktion. Sogar ein bisschen Relativitätstheorie steckt in dieser schlichten Gleichung.
Korteweg-de Vries, Sine-Gordon, Toda – das sind nur drei prominente unter zahlreichen Systemen, die Solitonverhalten zeigen und damit einerseits nichtlinear, andererseits auf verblüffende Weise „ordentlich“ sind. Wenn die linearen Systeme die Elefanten sind, was sind dann die Soliton-Systeme zoologisch gesehen? Es stellt sich heraus: Sie sind mit den Elefanten auf eine merkwürdige Weise verwandt. Aber das erzähle ich Ihnen beim nächsten Mal.


Das ist wieder ein Hinweis, das Physik, Mathematik und Naturbeobachtung zusammengehören.
Die Welle ähnelt der Gausschen Normalverteilung und das deutet auch darauf hin, dass viele chaotische Zustände doch wieder ein stabiles System bilden, nicht nur mathematisch/statistisch, sondern ganz real als beobachtbare Welle.
Ein super Artikel !!
Auf einer höheren Ebene sind nichtlineare Phänomene das Normal und sich ausbildende Ordnung in von nichtlinearen Phänomenen bestimmten Systemen die Ausnahme – wobei sich diese Ausnahme reproduzieren kann. Siehe Tier und Mensch, siehe Hirn. Und ja, es gibt auch ein Solitonenmodell der Nervenpulsausbreitung, wenn es auch nicht das Standardmodell ist. Das Standardmodell ist vielmehr das Hodgkin–Huxley Modell, doch Untersuchungen zeigen, dass folgendes gilt:(Zitat) „ Gemessene Temperaturänderungen sind völlig unvereinbar mit dem Hodgkin-Huxley-Modell“
Wer weiss: vielleicht können wir ja nur denken und empfinden weil Solitonen durch unser Hirn wandern.
> Wie war das? Elektromagnetische Wellen in Materie, zum Beispiel Licht in Glas, verhalten sich noch ziemlich ordentlich; eine lineare Theorie beschreibt das ganz gut.
Ich möchte da an ein Geschenk von Spektrum der Wissenschaft an die Abonnenten erinnern: Es sieht aus wie ein klobiger Kugelschreiber, enthält zwei AAA-Batterien und funktioniert selbst nach einigen Jahrzehnten noch einwandfrei.
Hermann Haken, der immer noch unter uns weilt, hat Mitte der Siebziger für ein vereinfachtes Modell die unlängst hier heiß diskutierten Lorenz-Gleichungen hergeleitet:
Physics Letters A
Volume 53, Issue 1, 19 May 1975, Pages 77-78
Analogy between higher instabilities in fluids and lasers
The Lorenz model of instabilities in fluids is shown to be identical with that of the single mode laser and applicable to undamped laser spikes. Further instabilities connected with small-band excitations are also discussed.
Das Zeigermodell von Feynman zeigt die Möglichkeiten auf, wie sich ein Lichtstrahl in Materie verhalten kann, welchen Weg der Lichtstrahl nehmen kann. Welchen Weg er tatsächlich wählt , das bleibt ein Geheimnis.
@Christoph Pöppe
»Entweder ist das System „fast linear”, will sagen, einem linearen System so ähnlich, dass man den Unterschied außer Acht lassen kann — zumindest für eine Weile. Das ist der Grund, warum unser Kalender jedes Jahr im Wesentlichen gleich funktioniert: Das Planetensystem ist zwar im Prinzip chaotisch, aber das macht sich erst nach ein paar Millionen Jahren ernsthaft bemerkbar.«
Ja, das Planetensystem galt deswegen auch lange geradezu als Sinnbild für ein himmlisches Uhrwerk. Aber eigentlich nicht, weil es “fast linear” wäre, sondern eher, weil es “fast integrabel” ist. In dem Sinne, dass die Bahnen der Planeten nahe bei den — im Prinzip zuerst von Kepler beschriebenen — Orbits eines integrablen Systems liegen.
Und Integrabilität erweist sich dann schliesslich irgendwie auch als der Schlüssel zum Verständnis des “ordentlichen” Verhaltens von Solitonen, das mit versteckten Symmetrien der KdV Gleichung korrespondiert. Aber es ist uns ja auch noch eine Fortsetzung versprochen…
Christoph Pöppe schrieb (04. Jan 2021):
> […] von einem plötzlich angehaltenen Schiff eine einsame Welle sich löste und durch den Kanal wanderte.
> […] Diederik Korteweg und Gustav de Vries die Sache in eine mathematische Gleichung fassen konnten: eine nichtlineare partielle Differenzialgleichung, die zum Beispiel so aussieht: […]
(Über die verschiedenen Geschmäcker der Formatierung, ganz besonders von \(LaTeX\)-Ausdrücken in SciLogs-Kommentaren, lässt sich bekanntlich nicht streiten. Vorteilhaft finde ich jedenfalls u.a. die Darstellung der Korteweg-de Vries-Gleichung als \[ \partial_t u = 6 \, u \, \partial_x u + \partial_{x x x} u. \]
> \(u\) ist die Höhe des Wassers über der Gleichgewichtshöhe, abhängig vom Ort \(x\) und der Zeit \(t\), und die Maßeinheiten sind gerade so gewählt, dass alle Vorfaktoren gerade gleich 1 bzw. 6 werden.
Sofern in der o.g. partiellen Differenzialgleichung ausschließlich dimensionslose (reell-wertige) Variable auftreten,
wäre \(u\) allerdings nicht “die Höhe” (der Wellenoberfläche über der (gedachten) Ebene des ungestörten Wassers) an sich, sondern (lediglich) eine Maßzahl, die das Verhältnis dieser Wellen-Höhe zu einer geeigneten Höhe bzw. Länge ausdrückt (welche sich aus der Tiefe des Kanals sowie weiteren “Versuchsbedingungen bzw. Materialeigenschaften” ergibt).
Auch wären “Ort \(x\)” und “Zeit \(t\)” wohl nicht (nur) irgendwelche Koordinaten, sondern ebenfalls Maßzahlen, die jeweils das Verhältnis eines bestimmten Maßes zu einer bestimmten geeignet gewählten Einheit ausdrückt;
insbesondere “\(x\)” das reell-wertige Verhältnis einer bestimmten Distanz (z.B. der Distanz zwischen dem Bug des haltenden Schiffes und einem bestimmten Bestandteil des Kanalrandes, der von der Welle passiert wurde) zur o.g. geeigneten (Maßeinheits-)Länge (ggf. einschl. eines Vorzeichens zur Darstellung von “Richtung”?),
und “\(t\)” das reell-wertige Verhältnis einer bestimmten Dauer (z.B. der Dauer des Schiffes von dessen Auslösen der Welle bis gleichzeitig zur Anzeige eines bestimmten Bestandteils des Kanalrandes bei Passage der Welle mit bestimmter Höhe) zu einer bestimmten geeigneten (Maßeinheits-)Dauer.
> […] dass es für die Gestalt der einsamen Welle eine explizite formelmäßige Darstellung gibt. Man setzt voraus, dass die Lösung der Gleichung sich in unveränderter Gestalt mit konstanter Geschwindigkeit bewegt
… wohl eher: dass eine Welle, die einer Lösung der Gleichung entspricht, sich in unveränderter Gestalt mit konstanter (und gleichmäßiger Phasen-)Geschwindigkeit bewegt …
> führt also ein mitwanderndes Koordinatensystem ein.
Anstatt Koordinaten einzuführen, lässt sich aus den o.g. Maßzahlen eine weitere (geeignete) dimensionslose Größe (“die Phase der Welle”) definieren; insbesondere
\(\phi := (x – t) – (x_{\text{Wellenkamm}} – t_{\text{Wellenkamm}} \)
(wobei die Phasen-Geschwindigkeit der Welle, bzgl. den Bestandteilen des Kanals bzw. dem haltenden Schiff, als Verhältnis der o.g. geeigneten Maßeinheiten von Länge und Dauer erhalten wird).
Indem Höhen-Maßzahl \(u\) (und damit “die unveränderliche Gestalt der einsamen Welle”) nun als Funktion dieser Phase \(\phi\) aufgefasst wird, ergibt sich aus der o.g. Korteweg-de Vries-Gleichung die (einfachere, “gewöhnliche”) Differentialgleichung
\[ u’ + 6 \, u \, u’ + u”’ = 0 \]
(u.a.) mit Lösung
\[ u[ \phi ] := \frac{1}{2 \, (\text{Cosh}[ \, (\phi / 2) \, ])^2} = \frac{2}{(e^{(\phi/2)} + e^{(-\phi/2)})^2} = \frac{2}{e^{\phi} + e^{-\phi} + 2} = \frac{1}{1 + \text{Cosh}[ \, \phi \, ]}.\]
(Diese Funktion \(u[ \phi ]\) weist gewisse Ähnlichkeit mit der im obigen SciLog-Artikel angegebenen Funktion \(u(x)\) auf. …)
Die o.g. jeweils “als Maßeinheit einer bestimmten einsamen Welle geeignete” Höhe bzw. Länge erweist sich damit als genau die doppelte Höhe ihres Wellenkamms.
> Es gibt sie in allen Größen. Je größer sie ist, desto steiler und zugleich schneller ist sie. […]
Hinsichtlich der gleichen Versuchsbedingungen (Kanaltiefe, Materialeigenschaften) lassen sich verschiedene Wellen-Phasen auch allgemeiner als
\(\phi := (x – c t) – (x_{\text{Wellenkamm}} – c t_{\text{Wellenkamm}} \)
definieren, wobei der Parameter-Wert \(c\) als Maßzahl das Verhältnis zwischen Phasen-Geschwindigkeit der entsprechenden Welle und dem Verhältnis der o.g. geeigneten Maßeinheiten von Länge und Dauer angibt (einschl. des “Richtungs”-Vorzeichens). Die Lösungen der entsprechenden gewöhnlichen DGs sind (u.a.)
\[ u_c[ \phi_c ] := \frac{|c|}{1 + \text{Cosh}[ \, \sqrt{|c|} \, \phi_c \, ]}.\]
(Und das besagt: Je größer \(|c|\), desto höher, steiler, schneller die entsprechende Welle.)
> Und wenn eine große einer kleinen begegnet, dann vereinigen sie sich nicht etwa, sondern die große überholt im Effekt die kleine. […]
> Norman Zabusky und Martin Kruskal 1965 bei Computersimulationen […] Bei dem Versuch, die Ergebnisse dieser Simulationen durch eine Näherungsformel zu beschreiben, probierten sie herum – und stellten fest, dass ihre Formel eine weitere exakte Lösung der Gleichung beschrieb!
Wie lautet diese “weitere exakte Lösung der Gleichung” genau ?
Frank Wappler schrieb (06.01.2021,18:27 o’clock):
> […] Indem Höhen-Maßzahl \(u\) (und damit “die unveränderliche Gestalt der einsamen Welle”) nun als Funktion dieser Phase \(\phi\) aufgefasst wird, ergibt sich aus der o.g. Korteweg-de Vries-Gleichung die (einfachere, “gewöhnliche”) Differentialgleichung […]
\[ u\prime + 6 \, u \, u\prime + u\prime\prime\prime = 0. \]
\[ u^{\prime} + 6 \, u \, u^{\prime} + u^{\prime} {}^{\prime} {}^{\prime} = 0. \]
Die gute Nachricht: Es gibt sie, und man kann sie explizit hinschreiben, was bei nichtlinearen Differenzialgleichungen eben in der Regel nicht vorkommt.
Die schlechte: Schön anzusehen ist sie nicht. Bereits bei zwei Solitonen wird es äußerst unübersichtlich, und je mehr Solitonen es werden, desto monströser ist der Formelausdruck. Zu allem Überfluss kann man die cosh- und sinh-Terme als Summen von Exponentialfunktionen ausschreiben – oder auch nicht – und den Bruch, der Übersichtlichkeit zuliebe, erweitern und irgendwelche Klammern ausmultiplizieren – oder auch nicht –, was die Gestalt der Formel bis zur Unkenntlichkeit verändert.
Eine einigermaßen ansehnliche Form der 2-Soliton-Lösung samt grafischer Darstellung findet man auf der Website von Klaus Brauer von der Universität Osnabrück zum Thema. Auf der Website von Stephen Anco und Marc Willoughby von der Brocks University in Ontario (Kanada) steht im Wesentlichen dieselbe Lösung. Aber ich fürchte, das ist nicht so einfach nachzurechnen.
Constantin Rasinariu vom Columbia College in Chicago hat aus der Frage eine Übungsaufgabe mit dem Softwarepaket „Maple“ gemacht. Dort gewinnt man immerhin einen Einblick in die Struktur der Lösung: \[u(x,t)=2 {\partial^2 \over \partial x^2} \log \det M(x,t) \;.\] Dabei ist \(M(x,t)\) eine \(n \cdot n\)-Matrix (\(n\) ist die Anzahl der Solitonen), und deren Einträge sind einigermaßen harmlose Lösungen einer linearen Gleichung. Näheres demnächst.
Christoph Pöppe schrieb (06.01.2021, 21:34 o’clock):
> Die gute Nachricht: Es gibt sie, und man kann sie explizit hinschreiben […] Näheres demnächst.
Vielen Dank für die profunde und zügige Antwort!
> hwied, 06.01.2021, 10:49 o’clock
> Das Zeigermodell von Feynman zeigt die Möglichkeiten auf, wie sich ein Lichtstrahl in Materie verhalten kann, welchen Weg der Lichtstrahl nehmen kann. Welchen Weg er tatsächlich wählt , das bleibt ein Geheimnis.
Na ja. Feynman hat in seinen Vorlesungen zahlreiche Beispiele präsentiert, z.B. https://www.feynmanlectures.caltech.edu/I_30.html Diese waren einleuchtend und halfen dabei, eigene Probleme zu lösen. Was man heute unter “Zeigermodell Feynman” findet ist eher gruselig.
Feynman hat diese Situation schon seinerzeit beschrieben. Im Seminar beim Caltech trug ein junger Physiker ganz neue Erkenntnisse vor. Meldet sich einer fragt: “Worum geht es hier eigentlich?”
Der Vortragende: “Das ist Fermis Theorie des Betazerfalls.”
Der Frager: “Ich bin Fermi. Darauf wäre ich nicht gekommen.”
Karl Mistelberger,
Physik kann unterhaltsam sein.
Was ich bis heute nicht verstehe, wasin einer elektromagnetischen Welle schwingt. Beim Wasser sind es die Wassermoleküle, die in Resonanz miteinander sich auf -und abwärtsbewegen.
Und wenn man bedenkt, dass eine Wasserwelle einen Tanker mit 200 000 BRT so einfach hochheben kann, das ist doch schon Zauberei. (nicht zu wörtlich nehmen)
Wenn man mal selbst gerudert hat, dann merkt man, dass die Bugwelle des Bootes versucht das Boot nach oben zu drücken, aus dem Wasser heraus. Im günstigsten Fall fängt dabei das Boot an auf der Welle zu reiten, also zu gleiten.
Was ich damit sagen will, ob eine elektromagnetische Welle auch Materie, die sie passiert aus der Bahn drückt ?
> Was ich bis heute nicht verstehe, was in einer elektromagnetischen Welle schwingt.
Richard Feynman Magnets: https://www.youtube.com/watch?v=MO0r930Sn_8
> Was ich damit sagen will, ob eine elektromagnetische Welle auch Materie, die sie passiert aus der Bahn drückt?
Ein großes Problem und dessen preiswürdige Lösung:
Chirped pulse amplification for lasers was introduced by Donna Strickland and Gérard Mourou at the University of Rochester in the mid-1980s, work for which they received the Nobel Prize in Physics in 2018.
https://en.wikipedia.org/wiki/Chirped_pulse_amplification
Karl Mistelberger,
Danke für die Links.
könnte man also sagen, ein Laserimpuls verhält sich wie ein Gummiband, wenn es gestaucht ist, also hochfrequent, hat es mehr Spannungsenergie als wenn es entspannt ist, also niederfrequent.
Einen Lichtstrahl könnte man also als eine in sich geschlossene Einheit betrachten, Wobei der “Anfang” des Lichtstrahles schon sein “Ende” beinflusst. ???
Anmerkung: Bei der Auslenkung von Materie durch ein elektromagnetisches Feld dachte ich an eine Wanderfeldröhre, die Elektronen beschleunigen kann. Oder ist es umgekehrt, dass das beschleunigte Elektron die Frequenz des elektromagnetischen Feldes erhöht. ?
hwied schrieb (07.01.2021, 10:23 o’clock):
> […] was in einer elektromagnetischen Welle schwingt [?]
“Elektromagnetische Welle” (ggf. auch “elektromagnetische Strahlung”) nennt man das Schwingen bzw. die wellen-mäßige Ausbreitung des elektromagnetischen Feldes;
insbesondere des elektromagnetischen Tensors \(mathbf F\) bzw. (jeweils hinsichtlich eines bestimmten Bezugssystems) jeder Komponente \(F^{ab}\) des elektromagnetischen Tensors, d.h. jeder Komponente des elektrischen Feldes und jeder Komponente des magnetischen Feldes, im Zusammenhang.
Das entspricht dem Auftreten des elektromagnetischen Feldes ohne Ladungen, also insbesondere “im Vakuum” (vgl. https://en.wikipedia.org/wiki/Covariant_formulation_of_classical_electromagnetism#Maxwell's_equations_in_vacuum).
> […] ob eine elektromagnetische Welle auch Materie, die sie passiert aus der Bahn drückt ?
Das Auftreten eines externen, gerichteten elektro-magnetischen Feldes “bei einer Testladung” (die zum gesamten Feld natürlich auch “ihren Anteil” beiträgt, der jedoch “im Großen und Ganzen gering” sein soll) geht mit Beschleunigung dieser Testladung einher. (D.h. aus geometrischen Bewertungen, insbesondere der messbaren Beschleunigung, lässt sich in Anwendung der Variationsrechnung auf die wahrscheinlichste Stärke und Richtung von Feldern zusammen mit der wahrscheinlichsten Verteilung von Ladung und Masse schließen.)
In den gängigen Darstellungen der Lorentzkraft wird offenbar sowieso ausschließlich das jeweils externe elektro-magnetische Feld berücksichtigt; während aus Darstellungen, die auch den eigenen Beitrag einer Testladung zum Gesamtfeld berücksichtigen und vom externen unterscheiden, die damit verbundene auf die Testladung ausgeübte Kraft bzw. deren Beschleunigung leider um so weniger ersichtlich ist.
Jede Veränderung einer Ladungsverteilung (bzgl. eines geeignet festgehaltenen, starren Bezugssystems) ist andererseits zwangsläufig mit einer entsprechenden “Veränderung des Nahfeldes” verbunden, und in besonderen Fällen auch mit “überproportionaler Veränderung des Fernfeldes” (wie z.B. der Ausbreitung von Feld-Wellen).
hwied schrieb (07.01.2021, 10:23 o’clock):
> […] was in einer elektromagnetischen Welle schwingt [?]
“Elektromagnetische Welle” (ggf. auch “elektromagnetische Strahlung”) nennt man das Schwingen bzw. die wellen-mäßige Ausbreitung des elektromagnetischen Feldes;
insbesondere des elektromagnetischen Tensors \(\mathbf F\) bzw. (jeweils hinsichtlich eines bestimmten Bezugssystems) jeder Komponente \(F^{ab}\) des elektromagnetischen Tensors, d.h. jeder Komponente des elektrischen Feldes und jeder Komponente des magnetischen Feldes, im Zusammenhang. Das entspricht dem Auftreten des elektromagnetischen Feldes ohne Ladungen, also insbesondere “im Vakuum” (vgl. https://en.wikipedia.org/wiki/Covariant_formulation_of_classical_electromagnetism#Maxwell's_equations_in_vacuum.)
Gepulste Laser haben im Gegensatz zu den kontinuierlich arbeitenden ein ziemlich breites Spektrum. Die Dehnung des Pulses resultiert aus der Dispersion
https://en.wikipedia.org/wiki/Chirped_pulse_amplification#/media/File:Chirped_pulse_amplification.png
Viele Beispiele gibt es z.B. hier:
https://www.rp-photonics.com/chirped_pulse_amplification.html
hwied schrieb (07.01.2021, 10:23 o’clock):
> […] ob eine elektromagnetische Welle auch Materie, die sie passiert aus der Bahn drückt ?
Das Auftreten eines externen, gerichteten elektro-magnetischen Feldes “bei einer Testladung” (die zum gesamten Feld natürlich auch “ihren Anteil” beiträgt, der jedoch “im Großen und Ganzen gering” sein soll) geht mit Beschleunigung dieser Testladung einher. (D.h. aus geometrischen Bewertungen, insbesondere der messbaren Beschleunigung, lässt sich in Anwendung der Variationsrechnung auf die wahrscheinlichste Stärke und Richtung von Feldern zusammen mit der wahrscheinlichsten Verteilung von Ladung und Masse schließen.)
In den gängigen Darstellungen der Lorentzkraft wird offenbar sowieso ausschließlich das jeweils externe elektro-magnetische Feld berücksichtigt; während aus Darstellungen, die auch den eigenen Beitrag einer Testladung zum Gesamtfeld berücksichtigen und vom externen unterscheiden, die damit verbundene auf die Testladung ausgeübte Kraft bzw. deren Beschleunigung leider um so weniger ersichtlich ist.
Jede Veränderung einer Ladungsverteilung (bzgl. eines geeignet festgehaltenen, starren Bezugssystems) ist andererseits zwangsläufig mit einer entsprechenden “Veränderung des Nahfeldes” verbunden, und in besonderen Fällen auch mit “überproportionaler Veränderung des Fernfeldes” (wie z.B. der Ausbreitung von Feld-Wellen).
Frank Wappler,
ist ein elektromagnetisches Feld nur eine Matrix, eine physikalisch/mathematische Größe oder ist es real, so wie Licht real ist?
Und wenn es real ist, was ich auch annehme, was schwingt dann im Raum ?
hwied schrieb (08.01.2021, 18:05 o’clock):
> ist ein elektromagnetisches Feld nur […] eine physikalisch/mathematische Größe
Noch nicht einmal eine geometrisch-kinematische Messgröße, die unmittelbar auf Koinzidenzbestimmungen (der “materiellen” identifizierbaren Beteiligten bzw. ihrer gegenseitigen Wahrnehmungen) hinausläuft,
sondern (lediglich) eine dynamische, aus geometrisch-kinematischen Messwerten abgeleitete Messgröße.
> nur eine Matrix [… oder] real, so wie Licht real ist?
Elektro-magnetische Wellen wirken auf (el.-mag.) Ladungen und sind damit jedenfalls im Prinzip wahrnehmbar; und werden je nach Intensität des schwingenden Feldes und Empfindlichkeit der Beteiligten auch wirklich wahrgenommen.
Um aus Datensätzen von individuell-einzigartigen Wahrnehmungen jeweils Messwerte zu gewinnen (meinetwegen als Matrix aus reell-wertigen Matrixelementen), die miteinander verglichen werden können, um z.B. wiederum deren “Schwingungen” zu bewerten, ist zunächst die sorgfältige nachvollziehbare Definition der entsprechenden Messgröße erforderlich, d.h. der Methodik bzw. des Operators, wie ein hinreichender Datensatz ggf. jeweils auszuwerten wäre.
Frank Wappler,
Die Maxwell – Gleichungen haben wir, die Maßeinheiten haben wir, wir können also damit rechnen. Und wir haben auch eine Modellvorstellung über das elektromagnetische Feld.
Unbeantwortet bleibt die Frage, was schwingt denn da.
hwied schrieb (09.01.2021, 09:28 o’clock):
> […] was schwingt denn da.
Richtung und Betrag (Größe) der Beschleunigung jeder vorhandenen “Testladung” (von konstanter Ladung und konstanter Masse).
Frank Wappler,
kleiner Scherz zum Abend.
Die geänderte Frage lautet :” Was bringt die Probeladung zum Schwingen ?”
Das Magnetfeld, Dummkopf!
Von der Existenz des Buches wusste ich seit den Sechzigern. Ausgeliehen um es zu lesen habe ich es nie. Vor einiger Zeit ist mir durch einen glücklichen Zufall ein garantiert ungelesenes Exemplar zugelaufen. Auch bei mir lag es lange ungelesen umher. Doch im vergangenen Herbst passierte es. Ich habe es von der ersten bis zur letzten Seite gelesen und fand es ausgezeichnet. Ich empfehle die Lektüre:
Albert Einstein, Leopold Infeld
Die Evolution der Physik
https://en.wikipedia.org/wiki/The_Evolution_of_Physics
@hwied
Der Impuls,der Zufall… 🙂
Karl Mistelberger,
Es geht bei der Fragestellung darum , was ein “Feld” ist. Genauer, es geht darum, ein anschauliches Modell eines “Feldes” zu finden, die mathematische Darstellung haben wir. Noch genauer, wie würden Sie einem 10 jährigen erklären was ein Magnetfeld ist. Sie können dem 10 jährigen einen Hufeisenmagneten in die Hand drücken. Dann bekommt er eine Vorstellung. Wenn er dann aber fragt, was ist in dem Magnetfeld drin , was antworten Sie ?
> Es geht bei der Fragestellung darum , was ein “Feld” ist.
Was ein Feld ist habe ich mich nie gefragt. Felder sind einfach da; so wie das Auto in der Garage. Da braucht es kein anschauliches Modell, das alles nur komplizierter macht.
Einstein und Infeld formulierten:
“Ein neuer Begriff taucht in der Physik auf, der bedeutendste seit Newton: das Feld. Die Erkenntnis, dass es bei der Beschreibung physikalischer Vorgänge weder auf die Ladungen noch auf die Partikeln, sondern viel mehr auf das in dem Raum zwischen Ladungen und Partikeln liegende Feld ankommt darf als wissenschaftliche Großtat angesprochen werden.”
Warum das so ist kann man nicht in einem Kommentar im Detail erläutern. Für einen Physiker ist es selbstverständlich. Dem Laien hilft das erwähnte Buch weiter.
Mussi,
Wenn Sie mit ihrem Auto in den Straßengraben gefahren sind und dem aufnehmenden Polizeibeamten erklären “ein zufällig vorbeikommendes Magnetfeld” hat mich abgelenkt, wie reagiert der Polizist.
a) er schreibt ernsthaft ihre Aussage auf
b) er schreibt schmunzelnd ihre Aussage auf
c) er antwortet ihnen freudestrahlend “Das ist mir gestern auch passiert”
d) er schickt sie zu einem Alkoholtest.
@hwied
was ist drin? Energie
wie sie funktioniert? Wechselwirkunsgmechanismus, ein Magnet ist hervorragend
was sage ich dem Polizisten? Impulskontrolle verloren: a-c
hwied schrieb (11.01.2021, 19:42 o’clock):
> Was bringt die Probeladung zum Schwingen?
Bis zu einem bestimmten Ereignis wird jeder Teilnehmer an diesem Ereignis offenbar jeweils durch diejenigen Ereignisse gebracht, an denen er/sie/es zuvor teilnahm;
einschl. aller dabei gemachten Wahrnehmungen (z.B. Wahrnehmungen von Signalanzeigen eines geeigneten “Senders”, von dessen geladenen Bestandteilen ggf. zu messen wäre, dass sie schwangen).
Frank Wappler,
die gemeinsame Teilnahme an dem Ereignis des Schwingens lässt vermuten, dass hier die Realität am Wirken ist.
Und nach ihrer Erklärung ist diese Realität gequantelt.
Wie wäre es, wenn wir so ein Quant ein Magnetquant nennen.
@hwied
nennt man bereits: https://de.wikipedia.org/wiki/Plancksches_Wirkungsquantum
Es gibt nicht nur das Magnetfeld der Erde. Es geht halt eben erheblich kleiner.
Da kann so ein Ding schon einfach mal so daher kommen… 🙂
Mussi,
sprachlich betrachtet sind die Physiker kein gutes Vorbild. Das Wirkungsquantum ist eben kein Teilchen sondern es ist u. a. der der Proportionalitätsfaktor zwischen der Energie E eines Photons und der Frequenz f der ihm entsprechenden elektromagnetischen Strahlung.
Karl Mistelberger,
wie kommt die Jungfrau zum Kind, wie kommt das Auto in die Garage ?
Es ist unbestritten, dass die Feldvorstellung die Elektrotechnik erst ermöglicht hat. Die Atomvorstellung hat auch die moderne Physik ermöglicht. Das ist alles unbestritten.
Ich suche nach Modellen.
Bei der Relativitätstheorie geht man davon aus, dass es die Gravitation als Kraft nicht gibt, sie ist eine Folge der Raum-Zeit-Krümmung.
Könnte man jetzt die Magnetkraft nicht auch als relativistische Folge von fließenden Ladungen ansehen. Dann entspräche das elektromagnetische Feld der Raumzeitkrümmung bei Massen.
@hwied
machen sie sich mal Gedanken zu dem “Phasenwechsel”…
Mussi,
meinen Sie den gametischen Kernphasenwechsel bezüglich der Jungfrau,
den Phasenwechsel bei einem Elektromotor
oder den Phasenwechsel beim Tauen von Glatteis ?
@hwied
…. 🙂 …sie kommen dem näher…im Grössten und kleinsten
> hwied, 13.01.2021, 08:57 o’clock
> Es ist unbestritten, dass die Feldvorstellung die Elektrotechnik erst ermöglicht hat. Die Atomvorstellung hat auch die moderne Physik ermöglicht. Das ist alles unbestritten. Ich suche nach Modellen.
Ich habe keine Ahnung, wozu die Suche nach Modellen gut sein soll.
Die Elektrodynamik beruhte ursprünglich auf mechanistischen Vorstellungen (“Modellen”). Das funktionierte im Alltag recht gut, erwies sich in der Folge aber als Klotz am Bein.
Den Gordischen Knoten hat Einstein zerschlagen: Das Licht ist wie es ist. Keine Modelle, bitte! Einstein und Infeld schließen das Kapitel “Der Niedergang des mechanistischen Denkens” im oben erwähnten Buch mit:
“Es besteht gar keine Hoffnung, die optischen Phänomene auf mechanische zurückzuführen, bevor diese Frage [worin sich das Licht ausbreitet] nicht geklärt ist, doch sind die mit der Lösung dieses Problems verbundenen Schwierigkeiten so groß, dass wir ein solches Vorhaben ganz aufgeben müssen, womit wir allerdings auch das ganze mechanistische Denken als überwunden anzusehen haben.”
Karl Mistelberger,
wie sag’s ich meinem Kinde.
Vom Durchschnittsbürger wird verlangt, dass er mit seinen Steuern Großprojekte finanziert. Cern in Genf z.B. Der Physiker muss sich also wenigstens bemühen verständliche “Vergleiche” zur Erklärung der Kernfusion zu finden. Der Lehrer in der Schule kommt ohne Modelle in der Unterstufe nicht aus.
Das Beispiel mit dem Licht. Der Lichtstrahl ist so ein Modell, den jedes Kind selbst sieht und versteht.
Ich meine keine mechanistischen Modelle, sondern Modelle die an Alltagserfahrungen anknüpfen. Das Wort “begreifen” trifft es sehr gut. Wenn der Aha – Effekt eintritt.
Nicht alle Menschen können mathematisch denken und bei einer Formel sofort erkennen, was da vor sich geht. Beispiel , die Schrödinger-Gleichung.
Wir sind jetzt 100 Jahre nach Einstein noch keinen Schritt weiter was den Doppelspaltversuch anschaulich erklärt. Mathematisch gesehen ist das klar, aber logisch ?
Beispiel Äther: Klar, ohne Äther hat die mathematische Vorstellung und Erklärung der elektromagnetischen Strahlung freie Fahrt.
Die Raum-Zeit-Krümmung, die ist auch ohne Äther.
Aber der menschliche Geist sucht nach einem Modell, und auf dieser Suche kommen wir auch beim Verständnis für das “Feld” weiter ?
Vielleicht sind wir in 100 Jahren weiter.
Physiker sind neugierig und rastlos:
The best moment came during Roger Penrose’s talk. Towards the end of a long and dense presentation of new ideas towards understanding the full space of the solutions of Einstein’s theory using twistors, Roger said rather dramatically that now he was going to present a new big idea that might lead to the twistor version of the full Einstein equations – but at that precise moment the slide projector exploded in a cloud of smoke, with sparks flying. We all thought for a moment that a secret power of the Universe, worried about being unmasked, had interfered. Could allying twistors and loops be dangerous?
https://cerncourier.com/a/when-twistors-met-loops/
@hwied,
Ich bin da eher pessimistisch. SIe haben da fast wörtlich die Frage gestellt, die gegen Ende des 19. Jahrhunderts die Physiker umtrieb: Was ist der Träger der elektromagnetischen Wellen? Ohne einen solchen –materiellen – Träger konnten sie’s sich nämlich nicht vorstellen. Sie nannten ihn “Äther” und erschlossen einige Eigenschaften, die er haben müsste. Es müsste so ein Glibber sein, der die ganze Welt gleichmäßig durchdringt und sehr merkwürdige Elastizitätseigenschaften hat. So ungefähr wie Asphalt, bloß um Größenordnungen labbriger. Wenn man nämlich auf Asphalt sehr langsam eine Kraft ausübt, weicht er aus und fließt. Wenn man es sehr schnell tut, schwingt er elastisch oder bricht sogar. Nur so konnte man erklären, wieso die Erde anscheinend ungebremst durch dieses Äthermeer schwimmt, während auf das viel schnellere Licht eine elastische Rückstellkraft wirkt (so etwas braucht man für materielle Wellen). Und außerdem müsste die Erde auf ihrem Weg durchs Weltall etwas Äther mit sich führen. Anders wäre das Michelson-Experiment nicht zu erklären gewesen (die Lichtgeschwindigkeit hat in allen Richtungen denselben Wert): Die Relativgeschwindigkeit der Erde gegen den Äther hätte sich ja bemerkbar machen müssen.
Die Physiker hatten also eine – sehr weit ausgearbeitete – Modellvorstellung, die auch durchaus laientauglich war. Zu dumm, dass sie an den experimentellen Fakten scheiterte, und zwar hoffnungslos.
Für den Verstand ist das eine Zumutung vergleichbar dem Teilchen-Welle-Dualismus. Man muss damit leben, dass die schönen anschaulichen Modelle ihre Grenzen haben. Wenn man diese Grenzen beachtet, sind die Modelle ja durchaus zu etwas zu gebrauchen. Aber ein Modell vom Äther, das an keine Grenzen stößt? Kann ich mir offengestanden nicht vorstellen.