Muss Mathematik kompliziert sein?
BLOG: Heidelberg Laureate Forum

Der französische Mathematiker Émile Lemoine soll einmal gesagt haben „Eine mathematische Wahrheit ist an sich weder einfach noch kompliziert, sie ist.“ Diese Weisheit scheint – mehr als 100 Jahre nach Lemoines Tod – nicht mehr weit verbreitet zu sein. Fragt man heutzutage Bekannte, Promis, vielleicht sogar die eigenen Verwandten nach ihrer Meinung zur Mathematik, klingen die Antworten meistens ähnlich: „Nee, Mathe fand ich immer zu kompliziert – und alle diese Formeln konnte ich mir auch nie merken.“ Oft mit einem gewissen Stolz in der Stimme. Am liebsten würde ich solchen Menschen – frei nach Florian Freistetter – zurufen: „Keine Ahnung von Mathematik zu haben ist nicht cool!“
Auch in den Medien hört man wieder viel von all‘ der komplizierten Mathematik, die wir z.B. zur Verschlüsselung unserer Email brauchen. Auch Bienen scheinen auf der Futtersuche komplexe Mathematik anzuwenden, und natürlich wissen wir seit Einstein, dass Planeten sich an komplizierte mathematische Gesetze halten, um nicht aus der Bahn geworfen zu werden. Natürlich geht es bei den letzten beiden Beispielen mehr um die Mathematik als Sprache zur Modellierung von Phänomenen. Interessanterweise lässt sich vieles davon in ganz normaler Sprache – z.B. Deutsch – formulieren. Uund jeder halbwegs konzentrierte Mensch versteht, worum es geht, und wundert sich auch nicht weiter darüber. Sobald es aber in Form von mathematischen Formeln auftaucht, weigern sich viele unserer Zeitgenossen schlichtweg, auch nur eine Sekunde darüber nachzudenken. Lieber sagt man dann „Nee, das ist mir zu kompliziert.“ Aber ist das wirklich alles so schlimm?
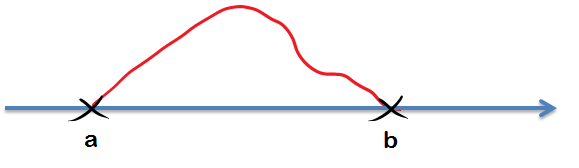
Betrachten wir als Beispiel einen Satz des Mathematikers Michel Rolle. Nehmen wir an, wir haben zwei Punkte a und b, die mit einer geraden Linie verbunden sind. Das könnte z.B. so aussehen:
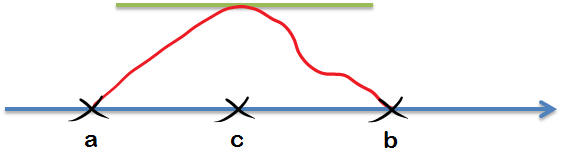
Jetzt verbinden wir diese beiden Punkte durch eine zweite Linie, ohne den Stift abzusetzen. Einzige Einschränkung: die Linie darf keine abrupten Richtungswechsel enthalten. Sie darf also keine „Zick-Zack“ Linie sein.
Rolles Satz besagt nun, dass es irgendwo auf dieser zweiten Linie mindestens eine Stelle gibt, an der die zugehörige Tangente die Steigung Null hat.
Das war’s. Kompliziert? Nicht wirklich.
Jetzt die mathematische Variante. Rolles Satz in der mathematischen Formelsprache klingt so:
Ich denke der Unterschied ist eindeutig. Aber das Spannende ist: der grundsätzliche Inhalt der Textform und der Formelform ist gleich.
Wieso verstehen wir dann das Eine besser als das Andere? Liegt es nur an diesen mathematischen Symbolen, wie z.B. dem „umgedrehten E“, die das Verständnis erschweren? Brauchen wir nur ein Wörterbuch „Mathe-Deutsch / Deutsch-Mathe“ erfinden und dann ist jeder von uns sofort ein Mathe-Genie? Wohl kaum. Aber das obige Beispiel zeigt, dass es oft einfach nur auf die richtige Darstellung ankommt, um Mathematik begreifbar zu machen.
Auf der anderen Seite gibt es in der Mathematik viele abstrakte Konzepte, die man wohl erst nach entsprechendem Studium versteht – schlichtweg, weil sonst die Grundlagen fehlen. Aber man würde sich ja auch nicht die Rettung des Bankensystems zutrauen, ohne vorher gewisse Grundlagen der Wirtschaft verstanden zu haben. (Ich weiss‘, was sie jetzt denken – glauben sie mir, diese Leute haben Berater, die eigentlich Ahnung haben sollten…)
Wohin also mit unserer Skepsis gegenüber der achso komplizierten Mathematik und dem Unwillen sich damit auseinanderzusetzen? Ich denke, in einer fortschreitend von Wissenschaft und Technik dominierten Welt, kann man sich das eigentlich nicht mehr leisten. Mathematik bzw. mathematische Modelle halten überall Einzug: in die Steuerung unserer Autos, die Berechnung des Flugticketpreises für unseren nächsten Urlaub, die Prämien unserer Versicherungen und natürlich auch in die verschiedensten Bereiche des Banken- und Finanzsystems. Ich verlange selbstverständlich von niemandem, sich jetzt mit all diesen wissenschaftlichen Abhandlungen und Theorien auseinanderzusetzen, um darin Experte zu werden. Aber ich würde mich freuen, wenn es mehr Interesse dafür geben würde, was Mathematik und ihre Anwendung eigentlich für uns bedeuten. Dass eine unverständlich aufgeschriebene und mit überzeugenden (oder abstoßenden) Symbolen durchsetzte Formel, z.B. bei der Berechnung der Zinses-Zinsen des nächsten Hauskredites nicht automatisch unverständlich ist. Sondern das wir alle in der Lage sind, viele Dinge davon zu verstehen. Wenigstens die grundsätzlichen Ideen.
Ich behaupte also: ja es gibt komplizierte Mathematik. Aber es gibt auch Mathematik, die wir mit unserem gesunden Menschenverstand verstehen und ihre Konsequenzen begreifen können. Und nur weil es kompliziert aussieht, muss es noch lange nicht kompliziert sein – und sollte deshalb nicht als Ausrede benutzt werden, um sich dem Thema Mathematik nicht zu nähern. Denn Mathematik kann uns in vielen Bereichen des Lebens eine Hilfe sein – wenn wir sie denn nur lassen…
Anmerkung:
Als Klaus Tschira seinen Wissenschafts-Preis „Klartext“ ins Leben rief, hatte er vermutlich eine sehr ähnliche Idee: wieso muss Wissenschaft eigentlich immer so kompliziert dargestellt werden? Mit seinem Preis ermutigt er frisch promovierte Naturwissenschaftler ihre Dissertation kurz und verständlich aufzuschreiben und der interessierten Öffentlichkeit zur Verfügung zu stellen. Eine Auswahl der Preisgewinner kann man hier nachlesen. Alle diese Beiträge sind wundervolle Beispiele dafür, dass Wissenschaft – und insbesondere Mathematik – eben kein „Buch mit sieben Siegeln“ sein muss. Sondern in den meisten Fällen anschaulich und verständlich erklärt werden kann und dabei oftmals sehr alltagsrelevante Probleme löst oder vielleicht auch erst aufwirft.



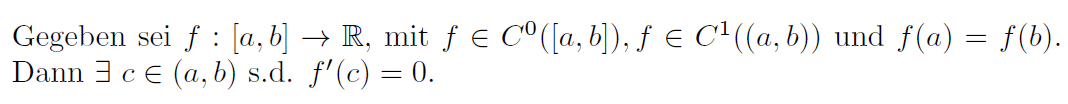
Die Mathematik-Inkompetenz vieler gebildeter Leute liegt am Mathe-Unterricht, den sie genossen haben. Egal ob man Sprachen lernt, Physik oder Mathematik. ernstzunehmen sind die Lernerfolge erst dann, wenn der Schüler mit dem gelernten selbst etwas anfangen kann. Beim Sprachenlernen bedeutet das, dass er in der Lage sein muss, die Sprache zu sprechen. In der Mathematik bedeutet es letztlich, dass der Schüler in der Lage sein muss, mindestens einfache mathematische Sachverhalte selbst zu formulieren. Der Satz von Rolle ist ein gutes Beispiel: Seine umgangssprachliche Formulierung verstehen die meisten und als nächsten Schritt werden sie auch die “Formelnotation” nachvollziehen können. Doch nur ganz wenige Ex-Gymnasiasten sind in der Lage – selbst wenn sie gut waren in Mathe – den Formalismus selbst herzuleiten und in der oben gezeigten Notation aufzuschreiben, selbst wenn sie den Satz begriffen haben.
Sinnfrage: Im Matheunterricht bekommt man meist nicht beigebracht, wofür das Gelernte gut ist und wofür es nützlich sein könnte. Daher schalten viele Schüler geistig ab, weil man keine Lust hat, sinnloses Zeug zu lernen.
Würde man von Anfang an nützliche Anwendungen in den Matheunterricht einbauen, dann hätte man ein völlig anderes Interesse von den Schülern zu erwarten – statt Desinteresse.
@Martin Holzherr: Das sehe ich genauso. Und das ist auch mein Punkt: man sollte an vielen Stellen weniger Wert auf die “Formulnotation” legen und das Wesentlich der Mathematik in den Vordergrund legen. Selbstverständlich wird das nicht immer funktionieren – aber wenn doch, dann ist das sicherlich ein Gewinn für uns alle.
@KRichard: Auch das kann ich absolut bestätigen. Und tatsächlich: es gibt solche Lehrer und Dozenten an Schulen und Universitäten, die an so vielen Stellen wie möglich die “Sinnfrage” stellen und auch beantworten. Auch dies funktioniert nicht immer, aber doch öfters, als man annehmen würde.
Abstrakte Mathematik ist nun einmal Mathematik und erschließt sich schon auf Grund der Notation dem Laien nur sehr schwierig.
Angewandte Mathematik bearbeitet eine Entsprechung in der Natur und kann oder könnte eher verstanden werden, zudem hat ja jedes Subjekt “seine” Mathematik.
MFG
Dr. W
Das was KRichard schreibt, kann ich so nur unterschreiben. Früher hab ich eine komplizierte Formel gesehen, da habe ich schon innerlich kapitoliert. Aber wenn einem das von einem Lehrer beigebracht wird, der das anders formuliert bzw. gut erklären kann, dann kapiert man es eher und dann kann Mathematik sogar Spaß machen.
Auf diese damaligen Standardsätze von den Lehrern, dass man Mathematik überall im Leben braucht, habe ich damals nichts gegeben, aber wenn man heute mal genau hinschaut, dann sieht man das anders. Das fängt ja schon an, wenn man handwerklich irgendwas basteln will und es mit Abmaßen zu tun hat oder in der Elektrotechnik, wo Stromstärken / Leistungen berechnet werden müssen. Irgendwo steckt überall die Mathematik drinne.
@Dr. Webbaer: Oft kann man allerdings in abstrakten mathematischen (Teil-)Gebieten Methoden finden, die sich auf anschauliche Dinge anwenden lassen. Und dann kann es in vielen Fällen auch interessant und verständlich für Nicht-Mathematikern sein bzw. werden.
Die Frage ist, warum nicht einmal die Wikipedia es schafft, so etwas verständlich rüberzubringen. Wäre ich als unbedarfter Mensch auf den Satz von Rolle gestoßen, hätte ich wahrscheinlich auch kapituliert.
Zitat:<i<"Anschaulich bedeutet dies: Auf dem Graphen der Funktion f gibt es zwischen zwei Kurvenpunkten mit übereinstimmenden y-Werten mindestens einen Kurvenpunkt mit der Steigung m = 0, also mit waagrechter Tangente."
@Gerald Fix: Das ist eine gute Frage – aber jeder kann ja bei Wikipedia für eine Verbesserung der Situation beitragen =)
Tim Conrad schrieb (23 September 2013):
> Betrachten wir als Beispiel einen Satz des Mathematikers Michel Rolle.
> Nehmen wir an, wir haben zwei Punkte a und b, die mit einer geraden Linie verbunden sind. […]
> Jetzt verbinden wir diese beiden Punkte durch eine zweite Linie, ohne den Stift abzusetzen. Einzige Einschränkung: die Linie darf keine abrupten Richtungswechsel enthalten. Sie darf also keine „Zick-Zack“ Linie sein.
> Rolles Satz besagt nun, dass es irgendwo auf dieser zweiten Linie mindestens eine Stelle gibt, an der die zugehörige Tangente die Steigung Null [gleich der Steigung der geraden Linie, die a und b verbindet] hat.
> Das war’s. Kompliziert? Nicht wirklich.
Das war’s?
Wohl nicht unbedingt (à propos “Rolle”).
> Jetzt die mathematische Variante […]
Ja: jetzt bitte “die mathematische Variante” des Satzes von Rolle hinsichtlich der abgebildeten “Rolle mit Helix”.
Hallo zusammen,
also ich bin definitiv der Meinung, dass Mathe nicht kompliziert sein muss. Für mich waren es Mathe sowie Physik zu Beginn.
Irgendwann habe ich mich durchgerungen und Nachhilfe in Anspruch genommen, wodurch Mathe tatsächlich “nicht kompliziert” war. Ich hatte einen hervorragenden Nachhilfelehrer, der selbst noch Student war und den ich über eine coole online Vermittlungsplattform namens http://www.nachhilfe-team.net gefunden hatte.
Also kommt es meiner Meinung unter anderem darauf an, wie einem das generell komplizierte Themengebiet Mathematik aufbereitet wird und wie viel man sich selbst damit beschäftigt.
Liebe Grüße, Basti