Math ⇔ Art: what is a rotogon?
BLOG: Heidelberg Laureate Forum

Alongside this week’s Laureate Forum, there’s an art exhibition on display in the nearby Old University building. Math ⇔ Art (Math is Art, Art is Math) is a collection of computer-generated artworks by Italian astrophysicist Aldo Spizzichino. In addition to a long career in research and many publications, Spizzichino has also produced an impressive quantity of mathematical art.
Using Fortran to generate computer graphics, Spizzichino has explored many mathematical shapes, structures and ideas through visual representation. The exhibit invites visitors to enjoy the mathematical forms for their own intrinsic beauty and, in Spizzichino’s words, ‘to complete the work with their own interpretation’.
Rotogons
One of the mathematical ideas included in the exhibit which I found particularly intriguing was that of the rotogon. Conceived by Spizzichino himself, these are solids created by rotating a shape around a given axis, and in particular around multiple axes at once.
Simply, you could imagine rotating a square around an axis running perpendicularly across the centre of the square. This would result in a cylinder, centred on the axis of rotation. Rotating around one edge of the square would also result in a cylinder, but a wider one.
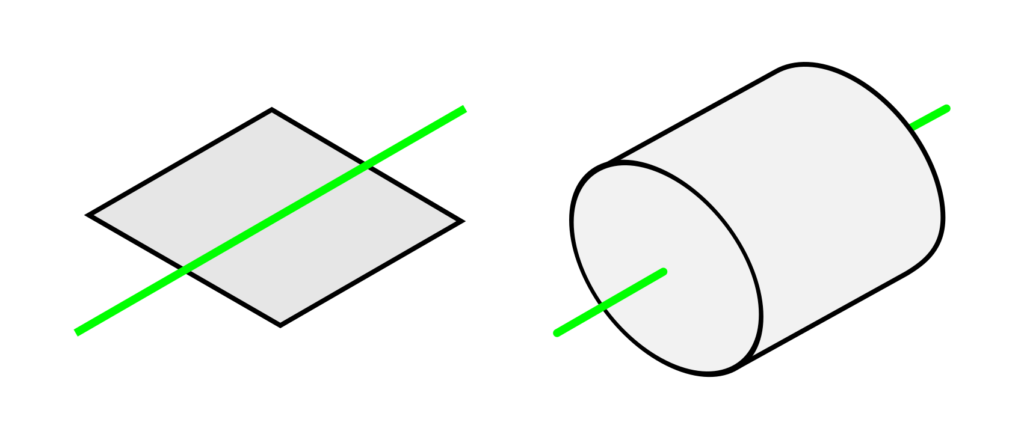 Square rotated around a perpendicular centre axis – resulting in a cylinder
Square rotated around a perpendicular centre axis – resulting in a cylinder
However, if you were to rotate the square around its diagonal, you would instead create a bicone.
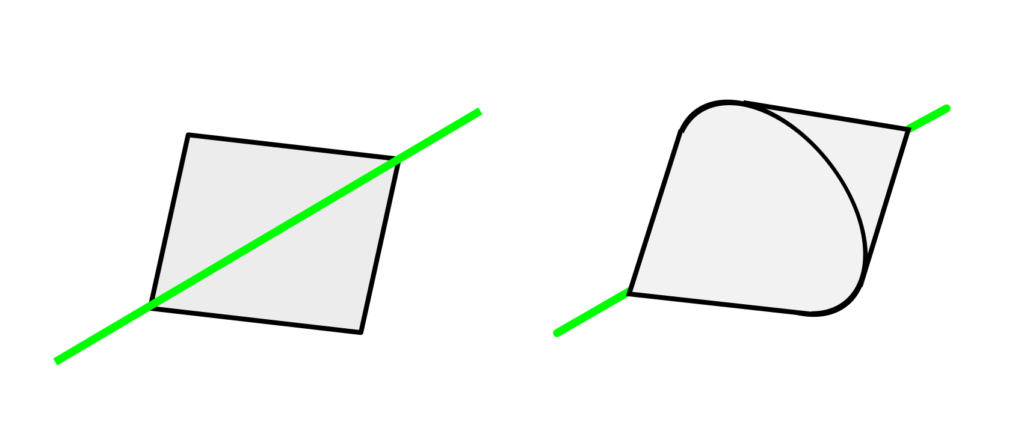 Square rotated around a diagonal axis – resulting in a bicone
Square rotated around a diagonal axis – resulting in a bicone
These shapes should be familiar to you already, although it can be a nice mental puzzle to work out what something will look like once rotated. This process becomes more interesting if you rotate the shape around more than one axis at once. For example, what would you get if you started with a square, and rotated it around both perpendicular axes at once?
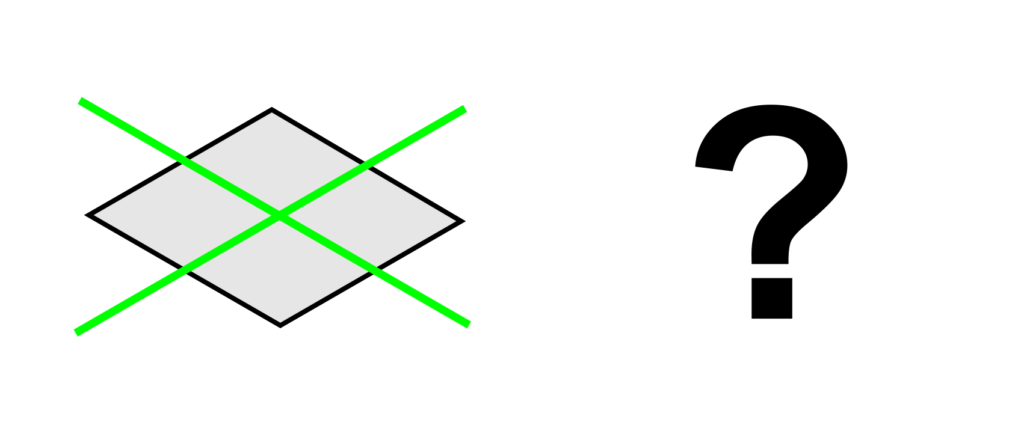 If you click on the image above, you’ll see the answer – but try to picture it first!
If you click on the image above, you’ll see the answer – but try to picture it first!
Spizzichino used his Fortran 3D graphics software to imagine many of the huge number of possibilities – rotating shapes in different directions, rotating around several edges or axes at once, and most interestingly, creating shapes by rotating 3D solids, or polyhedra – creating rotahedra.
Rotahedra
Spizzichino’s rotahedra have beautiful exteriors made from overlapping smooth curves in different directions, but also in many cases huge internal complexity. If you consider the original polyhedron to have been hollow, and visualise all the 3D shapes traced out inside the shape as well, interesting structures emerge.
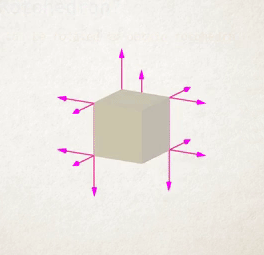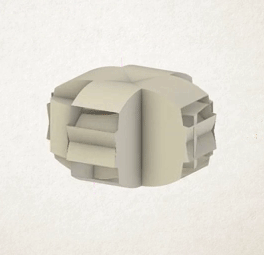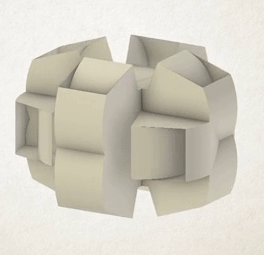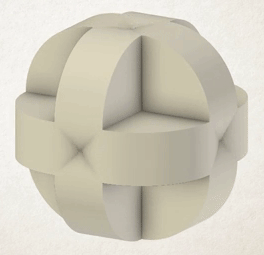
This animation (Eli Spizzichino, 2017) shows a cube being simultaneously rotated around all its edges. You can see the complex shapes created inside the object, before they’re finally covered by the outside layers of the shape as the cube completes its rotation.
One of the artworks in the exhibit shows a cross-sectional slice through one such shape – a rotogon based on a heptagon. Cross-sections like this reveal the internal structure of the shape and create beautiful images. Spizzichino points out that these internal slices are equivalent to looking at the pieces of the shape part-way through the rotating process.
Sadly, Aldo Spizzichino passed away in June 2017 while preparing for this exhibit, open daily (8:30-19:00) to the public until September 28, but his son Eli is present to talk to visitors about the pieces in the exhibition. Eli has continued his father’s work on rotahedra, and has produced an amazing video (including the animation above) using custom software in Blender. The video serves as an introduction to rotagons and rotahedra, and shows many beautiful examples. You can watch the video below.
More information
Information about the Math ⇔ Art exhibit on the HLFF website
Spizzichino’s gallery of works included in the exhibit, on his website
Spizzichino’s paper on rotagons and rotahedra (PDF in Italian, with images)



That’s awesome!
Spizzichino was not the first person to conceive of the Rotogon (aka Rotagon).