Infinity in your hands
BLOG: Heidelberg Laureate Forum

The Heidelberg MAINS (Mathematics Informatics Station) is an exhibition space in the centre of Heidelberg, created by the Heidelberg Laureate Forum Foundation for people to visit and explore ideas from maths and computer science through interactive exhibitions, galleries of portraits, film screenings and lectures. The MAINS is currently hosting an exhibition called Kein Ende In Sicht (No End in Sight), which is a travelling exhibit developed by the Mathematikum (an incredible mathematical museum based in Gießen), and is full of hands-on interactive activities exploring the topic of infinity.
The exhibition includes a range of approaches to the topic – demonstrations of physical manifestations of infinite series, build-your-own fractals, animations and even some attempts at perpetual motion machines! Though I’m sadly not going to be able to visit Kein Ende in Sicht while it’s in Heidelberg, I’m excited that people will be able to interact with infinity and play with these ideas in a tactile way – especially since some of them can be quite difficult to wrap your head around.
As the description of the exhibition points out, people commonly use words like ‘infinite’, ‘without end’ or ‘eternal’ – but often this can just be shorthand for ‘a large number’. The exhibition includes some examples of very, very large numbers – including the number of bacteria on a keyboard, the number of seconds since the Big Bang, and the largest known prime number (currently clocking in at 24,862,048 digits long). But all of these numbers are smaller – tiny, in fact, compared to infinity.
Count on it
It’s quite a big concept to hold in your head – the idea of something that goes on forever – and it’s something many people never really need to engage with too much in their daily lives.
But people happily work with elements of an infinite set every day – numbers. Whole numbers, or integers, are sometimes called counting numbers, because they’re used for counting whole objects. The process of counting a set of objects is often considered to be the same as matching up the objects in the set with counting numbers, starting from 1 – the size of the set is the largest number you’d use. These numbers form an infinite set, starting from zero and going on forever.
The size of this kind of infinite set, where you have a simple list of items that goes on forever, is called ‘countable infinity’ – if I wanted to, I could match up each item in the list with one of the counting numbers, and just keep going on forever. This often involves a little fiddling to make it work, but it’s always possible for a countably infinite set.
For example, if I wanted to include negative numbers in my list, I could order them as follows: 0, 1, -1, 2, -2, 3, -3… alternating between positive and negative. I’ve got a rule for how to order them, and can pair each one up with a counting number, so they’re countable. Or, if I wanted to just count the positive even numbers, I could go: 2, 4, 6, 8… – using the simple rule or pairing each even number 2n up with the counting number n, and keep going quite happily forever.
It sometimes surprises people to find that the set of positive even numbers, which misses out exactly half the numbers, somehow has the same size as the notionally larger set of all positive numbers. (This fact is made use of in the story of Hilbert’s hotel, included as one of the stations in the exhibit). This is one of the many ways in which infinity misbehaves, and why it’s not considered to be a number by mathematicians. Infinity plus one (if you can imagine such a thing) is still infinity, as is two times infinity – it doesn’t follow the normal rules of arithmetic.
Even if your infinite set seems like it must be bigger than a countable infinity, you might still be able to count it. The set of (positive) rational numbers – fractions, with a whole number on the top and bottom, form a countably infinite set.
This seems impossible since there are infinitely many possible numbers on the top and bottom of each fraction, which means we somehow have ‘infinity times infinity’ numbers; also, between any two fractions you can name, there will always be another fraction – surely this set can’t be counted?
Nonetheless, if you arrange them all in a two-dimensional square grid, with the top number increasing across the columns, and the bottom number increasing down the rows, you’ll be able to write out all the fractions – there’ll be some repeats, but they’ll definitely all be there. Then you can proceed from the top left corner of this grid, moving diagonally and snaking across the rows as shown, matching each new fraction you meet with a counting number, to show that the rational numbers are indeed also countably infinite.
With a small modification, this can be extended to include negative rational numbers as well. But there are some sets of numbers you can’t adapt this proof to count.
Out for the count
The existence of countable infinity implies that some infinities are uncountable – and most people are already familiar with an uncountably infinite set. If we go one step further than fractions we get the real numbers – all possible points on an infinite number line, including whole numbers, fractions and numbers with infinite non-repeating decimal expansions – and much like the rational numbers, there are infinitely many more numbers to be found in between any two you choose.
But this set is somehow ‘bigger’ – as proven by Georg Cantor, a German mathematician who developed a lot of these ideas around sets, infinity and counting. It’s sufficient to prove that one tiny section of the number line – the numbers between zero and one – is uncountably infinite, and this then extends to the whole number line.
One argument Cantor used to show the reals are uncountable relies on ‘proof by contradiction’ – we start with the assumption that there are countably infinitely many real numbers between 0 and 1, and attempt to write this infinite list. Each entry in our list will begin ‘nought point’, followed by an infinite decimal expansion (which could be anything, including a repeating sequence of digits, or even a sequence that’s just zeroes forever after a short while). Imagine them all written out, extending infinitely off to the right, and infinitely down the page.
Cantor’s idea was to consider what would happen if we look down the diagonal of this page. The first entry on the diagonal will be the first decimal digit of the first number, the second will be the second digit of the second number, and so on. The trick is to build a number by taking each entry in this sequence, and choosing a digit that’s not the same as it – if our first diagonal entry was a 3, we could choose a 4, for example. Continuing this process down the page will build an infinite decimal number, and if we pick a rule (e.g, ‘add one to the digit’) we can go on forever and generate the entire number.
The important thing is that this number is guaranteed not to already be in the list. It’s not the first entry in the list, as it definitely differs in the first position; nor is it the second entry, and so on. The number is new – it wasn’t on our list, but the list was infinite and supposed to include all the numbers, so our assumption that the set was countable can’t be true. This means some infinities are bigger than others! This proof – known as Cantor’s Diagonalization Argument – is a beautiful piece of mathematics, and connects to some really deep mathematical questions about the nature of infinity.
Many of the ideas discussed here are realised as part of the No End In Sight exhibition, using visualisations and demonstrations to make them more accessible (and if you prefer your fractions to be written on t-shirts worn by people running around and lining themselves up to demonstrate mathematical ideas, you’ll be very pleased). The exhibition itself, which is sadly finite, will only be running through until the 16th January – so make sure you go and visit while you can!



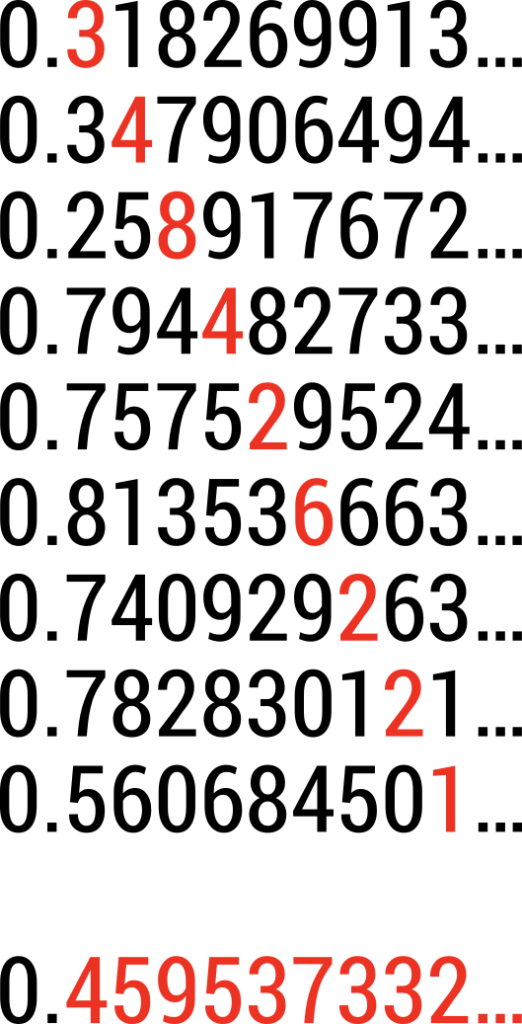
Katie Steckles wrote (27. Oct 2021):
> […] to build a number by taking each entry in this sequence […] The number is new – it wasn’t on our list
So — starting out with a (very schematic) list:
0 a aa aaa aaaa aaaaa ...some particular number
bcan be thought of (as having been built to completion) which is explicitly not in the sketched list.There may even several distinct numbers similarly constructable, many of which may be schematically listed as
b bb bbb bbbb ...which are explicitly different from any entry involving any
a.Then how about listing instead:
0 a aa ab b bb bbb abb aab aaa aaaa aaab aabb abbb bbbb abbbb ...Surely, by the construction sketched in the SciLog article above, some particular number
ccan be thought of which is explicitly not that suggested list, either.There may even several distinct numbers similarly constructable, many of which may be schematically listed as
c cc ccc cccc ...Consequently consider listing
0 a aa ab b bb bbb abb aab aaa aac ac c bc abc bbc bcc acc ccc cccc accc bccc bbcc abcc aacc aaac aabc abbc bbbc bbbb abbb aabb aaab aaaa aaaaa ...Surely, by the construction sketched in the SciLog article above, some particular number
dcan be thought of which is explicitly not that suggested list, either.There may even several distinct numbers similarly constructable, many of which may be schematically listed as
d dd ddd dddd ...Consider therefore listing …
(And so on.
Just refrain from imagining that the successive production of ever-larger completed initial segments of an infinite list could end up producing the complete list explicitly.)
Frank Wappler wrote (27.10.2021, 18:53 o’clock):
> […] Then how about listing instead:
>
0 a aa ab b bb bbb abb aab[…]So — which real number is “
ab“ supposed to represent in the given context, for instance? And (even) “bc“, etc. ?? …Well: I’m afraid that I cannot think of a defensible (and be it ever so symbolic) interpretation — sorry; much less had I already thought of one when posting my above comment.
(The sketched lists might however be relevant in other contexts, such as listing all ordered sets of finitely many numbers.)
The mathematical concept of an uncountable set is easy to understand but it raises the question: are there also uncountable items in our real world? Do we need uncountable sets to explain our universe?
The web site Does physics require a continuum? denies the need for a continuum in physics and even states:
One of the many consequences: It is impossible to design a computer with unlimited performance, because every computer requires physical resources. And these are limited!