Remember the artificial intelligences (AI) used in games like chess and Go, and how we said they are only a stepping stone for more impactful projects? Well, those impactful projects are arriving. After creating an AI that predicts protein shapes, one of the greatest challenges in modern biology, the DeepMind laboratory has now created an AI that broke a decades-old record for computational efficiency and can multiply matrices faster than ever before. Far from being just a theoretical achievement, this has big practical implications, as it could boost computational efficiency significantly in some fields

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions that are arranged in rows and columns. Matrices are often used to represent a mathematical object or some properties of mathematical objects. Matrices play an important role in many fields, ranging from algebra and graph theory to various fields of physics, like electronics and quantum theory. Matrices are also important in many computational problems.

For instance, matrix multiplication is often found at the core of image processing and compression, speech recognition and generating [MN2] computer graphics. This operation of multiplying matrices is often done by the Graphics Processing Unit (GPU), which consists of hundreds of smaller cores – in contrast to the Central Processing Unit (CPU), which typically consists of 4-8 larger cores. Having a parallel architecture enables more efficient matrix calculation, which in turn makes all the processes not only faster but also more efficient in terms of energy consumption.

But there’s still plenty of room for improvement, as DeepMind showed.

Multiplying matrices

Matrices have a long history of being used in mathematics (although the name ‘matrix’ only came up in the 1800s and they were called arrays before that). An ancient Chinese text known as The Nine Chapters on the Mathematical Art, written by multiple scholars from the 10th to the 2nd century BC, is the first example of using arrays to solve simultaneous equations. That’s also when the concept of a determinant came up.

Matrices were used for all sorts of things, but when they were multiplied, simple methods were commonly used.

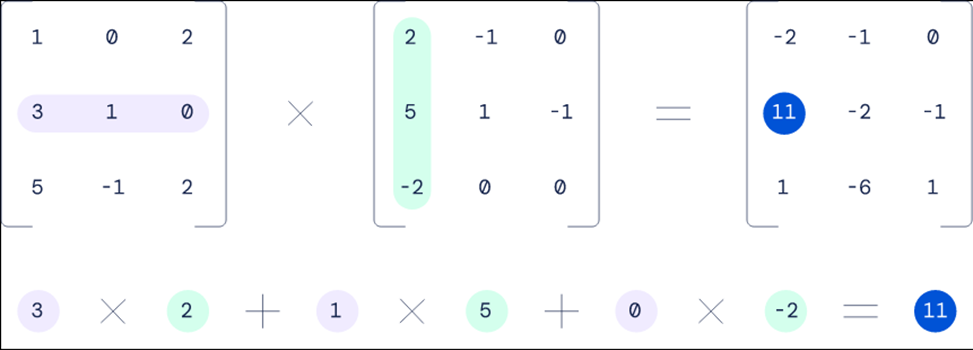
But in 1969, a German mathematician named Volker Strassen developed a new algorithm to multiply matrices. It was a shocking development, as Strassen showed that the method that had been used for decades or centuries could be improved upon.

When schoolchildren are taught to multiply matrices, they use a brute-force approach: you multiply the matrices row by column. For a 4×4 matrix multiplication, you need to do 64 operations. But with Strassen’s approach, you only need to do 49.

Comparison between a standard algorithm and Strassen’s algorithm. Image via DeepMind.

Strassen’s work was transformative, not necessarily because his algorithm was the most efficient, but because he showed that more efficient algorithms for matrix multiplication do exist. In fact, his research spurred several algorithms that were more efficient than his. However, for most types of matrices, we still do not know what’s the most efficient algorithm and there could still be room for improvement, but no one was able to demonstrate it.

This is where the new algorithm comes in.

After AlphaGo and AlphaFold: AlphaTensor

DeepMind uses a gamified approach to train its new algorithm:  reinforcement learning.

Reinforcement learning is a type of machine learning training method where the algorithm is ‘trained’ using feedback data that reinforces ‘correct’ behavior (behavior that leads the algorithm to its goal). For instance, when the algorithm is working towards a multistep goal (such as winning a board game), its parameters are updated when it makes winning moves, to make future success more likely.

AlphaTensor, as the algorithm was called, incorporates another feature (a tensor is a mathematical object used to describe physical properties, often thought of as a generalized matrix). It has a game-playing method called a tree search. Essentially, while the AI is calculating its next move, it is also looking at the branching options and assessing which option is the most promising. In order to do this, it asks a neural network to predict the options most likely to lead to success, and – while the algorithm is still learning – the neural network uses the outcomes of previous games as feedback.

Except, in this case the ‘game’ is not chess, but rather a representation of algorithmic operations. For the algorithm, each game starts out as a one-player puzzle where you have a three-dimensional tensor (a sort of matrix cube) filled in and the goal is to zero out its entries. 

“When the player manages to do so, this results in a provably correct matrix multiplication algorithm for any pair of matrices, and its efficiency is captured by the number of steps taken to zero out the tensor,” DeepMind explained in a press release.

The problem is, unlike chess where you have a fairly limited number of choices for each move, here you have an almost endless number of possibilities. You need the agent to select from quite literally trillions of possible moves, which makes navigating the learning space quite difficult. But it seems to be working out.

AlphaTensor has already discovered thousands upon thousands of functional algorithms – over 14,000 for the 4×4 matrices alone. In a 4×4 matrix where old-school methods would require 64 steps and Strassens’ algorithm requires 49 steps, AlphaTensor found a way to bring it down to 47. This may not seem like much, but it’s an improvement of over 4% which is already important. However, this improvement is even better on larger matrices.

According to tests performed by DeepMind on commercial hardware, these algorithms multiplied large matrices 10-20% faster than the currently used algorithms. This increase in performance was accentuated by the fact that the algorithms can be tweaked for specific hardware. For instance, some algorithms on one GPU (or CPU) may not be the fastest on others due to the hardware architecture, and this customization brings practical advantages.

But this isn’t the end of the story.

Improvements on Improvements

In one example, AlphaTensor managed to find a way to perform a 5×5 matrix multiplication in 96 steps – reducing it from 98 steps with the older method. But a team of researchers from Austria published a paper detailing how they have reduced that count by one, bringing it down to 95. This isn’t a coincidence: they used AlphaTensor’s results and built on them.

“This solution was obtained from the scheme of [DeepMind’s researchers] by applying a sequence of transformations leading to a scheme from which one multiplication could be eliminated.”

In other words, while it is still early, it seems like we are seeing a flurry of progress in matrix multiplication, just like what happened after Strassen published his result. It is a remarkable application of AI fueling new research, and it may happen in multiple fields.

Mathematics (and research, in general) often builds on itself. When a roadblock is encountered, it is hard to make any progress – but once even small progress is made, it can cascade into a number of new findings. We may see other longstanding mathematical paradigms being changed by algorithms. In fact, progress in technology often builds on itself too, so we may even see algorithms bringing progress into the field of developing algorithms. Increasingly, the collaboration between machine learning and human intellect is leading to new and exciting discoveries in various fields of research.

DeepMind also hopes that this recent work will inspire others in “using AI to guide algorithmic discovery for other fundamental computational tasks.” The strategy of starting with games and then moving on to other fields seems to be working out for now.