Game, SET and maths

Once a month my friends and I meet to have a drink in our local pub, and to discuss mathematics (of course). As part of our monthly MathsJam (for more information, and to see if there’s one near you, visit mathsjam.com) we solve puzzles, work out mathematical proofs and discuss interesting ideas. We also often play games, and one particular favourite – that usually comes out when new attendees join us – is the game of SET.

SET is a simple card game, which was designed by geneticist Marsha Falco in 1974. The original idea came when Marsha was comparing genetic traits in dogs, and devised a system of symbols drawn on cards, to track the different genetic features, and found a fun game could be made by finding sets of cards with particular traits. After refining the game, playing it with family and friends, Marsha started her own company and published the game commercially in 1990. While the game itself is simple and can be played by anyone with a few minutes of explanation of the rules, there are many interesting underlying mathematical ideas and structures.

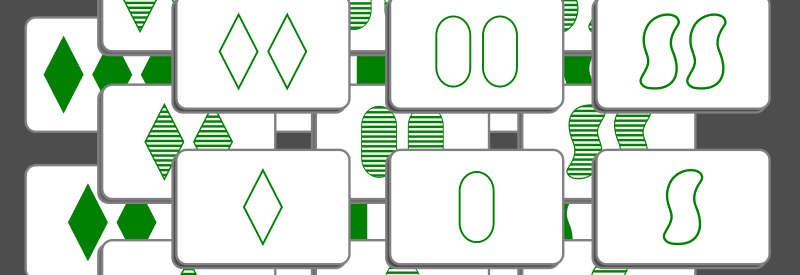
The game consists of a deck of cards, each containing symbols with different properties. Looking at these sample cards, you can see that the four possible properties a symbol can have are: colour, shape, number and shading. Each of these four properties can be one of three things:

• Colour: symbols can be red, green or purple
• Shape: symbols can be a diamond, squiggle or oval thingy (if you want a proper name for it, it’s called a stadium, but is apparently sometimes called an obround, or a discorectangle, which is my new favourite word)
• Shading: symbols can be blank, striped or filled
• Number: there can be one, two or three symbols on the card

This means that for each card, each of these four properties is set to one of these three values, and in a standard deck of SET cards, exactly one of each possible card is present. If you’d like to take a moment to work out how many cards there must be in a SET deck, please go and do that now before reading on. I’ll put the answer at the bottom of this post.

Given a structure like this, you can arrange the cards in rows which share properties. For a simple example, imagine taking only part of the deck (a sub-SET, if you will) in which all the cards are green, and filled in, and arranging them in a square. You could set up the square so that each row contains cards with the same number of symbols, and each column contains cards with the same shape.

If we wanted to include more cards, we could create a version of this 2D array for each of the three shadings, and then stack them on top of each other, to form a 3D cube.

To include the red and purple cards as well, we’d need three such cubes – and you can think of this as a hypercube: a four-dimensional cube, in which the colour axis extends off in to 4D, and you can’t visualise it as a single object in our limited 3D universe, but the three different cubes are ‘lying on top of each other’ in 4D, just as the square arrays stack up to make the 3D cube (and by analogy, the way the straight line sets of three cards stack up to make each square).

This underlying structure is barely noticeable to anyone just casually playing the game, but it is there, and in fact many familiar games can be abstracted in this way – for example, the game Dobble, marketed in the US as Spot-It, has a superb mathematical structure called a projective plane which underlies the way the symbols are arranged on the cards. But that’s a story for another time. I haven’t even told you how to play this game yet!

How to play

Gameplay involves competing to find a SET, where the definition of a SET is a specific combination of three cards, as follows: For each of the four properties, the three cards in the SET have to either be all the same for that property, or all different. For example, the cards could be all red, or there could be one red/one green/one purple. This has to also hold for each of the four properties – so you could have, say, all cards with three symbols on, or cards with 1, 2 and 3 symbols on. You can combine ‘same’ and ‘different’ across the four properties, as long as each individual property has the cards all the same, or all different.

If you’re not quite sure what that means just yet, make sure you untangle it – it’s a slightly knotty concept at first, but it’s equivalent to saying that in any collection of three cards, if you can see two cards which share a property that the third one doesn’t, it’s not a SET. Some examples of valid and invalid SETs are given in the diagrams below.

If you consider the 4D hypercube of cards we constructed earlier, each of the rows and columns (and whatever you call the lines running in the other two directions) of that hypercube will give a valid SET, as will any diagonals (of which there are quite a few, including diagonals within the layers – if you want to work it out, I’ll put how many there are at the bottom of the post).

If you rearrange the hypercube, by changing the order in which you put the rows and columns and whatevers and thingybobs, you’ll get another valid SET hypercube which will consist of all valid SETs too, and this can be done in many different ways. We had a go at laying out the cards in such a hypercube in the pub once, but we had to do it as nine separate squares on the table, so you have to imagine the fourth dimension.

If you’re playing with a group of people (for example, in a pub) you can start the game by dealing 12 cards onto the table. Then, if someone in the group thinks they’ve found a SET, they can shout ‘SET!’ and claim their three cards. (We’ve found through experience that requiring a clear audible signal before reaching in for the cards drastically reduces the incidence of hand collisions and fingernail gouging from too-enthusiastic SET grabs). For any SETs you successfully claim, you can keep the cards, and if you mistakenly shout ‘SET’ but can’t find one, you have to give one card back to the dealer as a penalty. Whoever holds the most cards at the end is the winner.

Some more puzzles

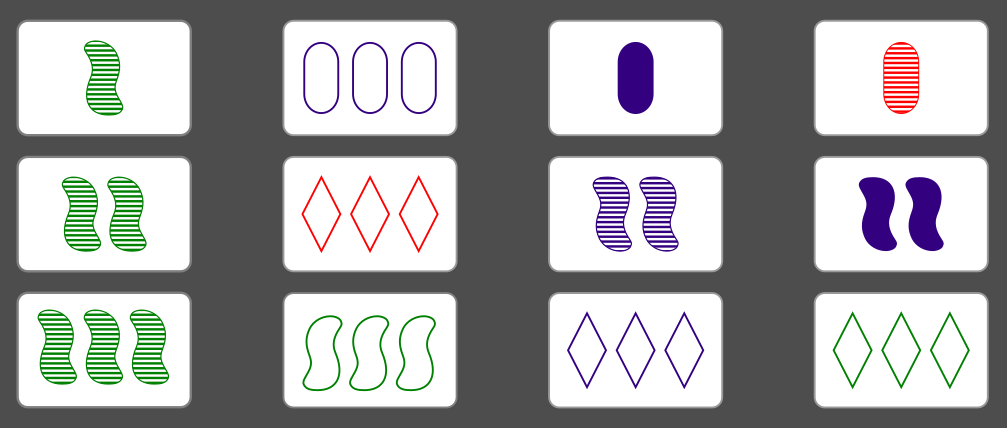
Any two cards in this game define a SET – much like the way in which any two points in 2D or 3D space define a unique line, and the two cards are points in the 4D space in which SET lives. Given two cards, it’s easy to work out what the third would be. Try these examples – what card should be at the bottom of each column? I’ll put the answers at the end of the post.

Finding the third card that’s missing from a SET like this is a nice exercise to practise and get better at spotting when a set of three cards is a SET. Each single card in SET is part of many different sets (go ahead and work out how many – I’ll put the answer at the bottom!) and since there are four properties that can be the same or different, there are different ‘levels’ of SET difficulty – the easiest being a SET where three of the four properties are the same and one is different, and the hardest where all four properties are all different. (It’s not possible to have a SET where all four properties are the same, as there’s only one of each card).

If you’d like to both test your mental agility and own a four-dimensional object that fits in a small box, you can buy copies of SET online from various places, and in (or so I’ve found) only the most excellent board game shops. It’s also been variously available as a mobile app in official SET enterprises and less official versions, so you can hone your skills before your next pub session.

There are plenty of other puzzles around the game too, many of which are outlined in a book, The Joy of SET, published in 2016 by a family of SET fans – including questions like, what’s the most cards you can deal out on the table and still not have a SET? And, what’s the probability that your initial deal of 12 will contain at least one SET? But of course the most important question you might ask yourself is, will we be able to fit in another game before the pub closes?

Solutions

Here follow the answers to the little problems I’ve… SET you (sorry)… during this post.

How many cards in a standard SET deck?

If each card has three choices for each of the four properties, the number of possible cards is 3 × 3 × 3 × 3 = 81.

How many different diagonal lines are there in a 3 × 3 × 3 × 3 hypercube?

There are two diagonals in a 3 × 3 square, and to work out the number in a cube you can see there are two in each plane of the cube (three in each of three directions), giving 9×2=18 diagonals lying inside planes; then you simply need to count the diagonals running from corner to corner, and with eight corners on a cube there are 4, so a 3 × 3 × 3 cube has 22 diagonal lines within it. Then to go up to a hypercube, you’ll need 22 for each of the three cubes it contains, times the four dimensions, and then add the number of diagonals running between opposite corners – 8, pairing up the 16 vertices on a hypercube. So the total is (22 × 3 × 4) + 8 = 272.

What’s the missing third card in each SET?

How many SETs is one given card a member of?

For each card, there are 80 other cards in the deck it could be paired with. Picking each one of these 80 cards will give you two cards, which will define a SET. However, each of these SETs will be present twice, as you’ll get the same set whichever of the two other cards in it you pick, so you have to divide by two and find that each card is part of 40 sets.