Flexagons and false advertising

At home I have a large box of A4 paper I use for my printer, and am always amused when I look at the box just how desperate the manufacturers are to impress you with their paper’s wonderful properties – as well as its ‘Maximum Quality’ (apparently, 5 is the maximum) and ‘Vibrant Colours’ (the paper is white, so I assume you have to provide the colours yourself) it also includes ‘Double Sided Use’. This would be something I’d expect of basically all paper, as it’s a flat object with two sides, and I’m unimpressed. However, it’s possible to get more sides for your money using mathematics, by making your paper into a flexagon.

Flexagons were discovered by mathematician Arthur Stone (right), when he moved from the UK to study at Princeton University, in the USA. He discovered that his British binder wasn’t the right size for the US sizes of paper. So each sheet of paper he used for his notes had to be trimmed, and he found himself with a pile of leftover strips of paper, which he naturally started to fiddle with. Stone noticed that by folding the paper, he could create an interesting hexagonal shape.
Try it now for yourself – get a strip of paper, of any width, and fold it into a strip of equilateral triangles. Make all your folds carefully creased, and fold them both ways so they’re nice and flexible. Once you have ten triangles in a row, fold the left hand three triangles behind, and then make a second fold, bringing the right hand end towards you, three triangles along, so you have a hexagon shape with one extra triangle sticking out. Tuck the extra triangle part behind the other part – this should be the end of your strip, and should be next to the other end triangle. Fold it over and glue these two end triangles together, so you have a closed loop of triangles forming a flat hexagon (and if you’ve done it right the gaps under the strip will all be oriented the same way). Flat means two-sided, right? Well, no. What you’ve made is a hexaflexagon – and with flexagons, it’s rarely that simple.
If you label the two faces of your hexagon (by writing a number, or drawing a dot of colour in the middle of each triangle), you’ll be able to tell them apart and keep track of them. If you now ‘flex’ your flexagon – by bringing three spaced out corners together in the middle, then opening the flexagon from the other side, you’ll find a third, unlabelled face, mysteriously appears. The claim made on the paper box now seems like an understatement – the paper now has triple-sided use!
The flexagon you’ve just made is called a tri-hexaflexagon (it’s a hexagon, and it has three faces) but it’s also possible to make a hexa-hexaflexagon, with six magical hidden faces, using a longer strip of 19 triangles and a lot more folding. It’s also possible to make square flexagons, called tetraflexagons, and three-faced and six-faced variants are easy to make. Other shapes and numbers of faces are also possible – and Stone, along with some of his Princeton colleagues, formed a Flexagon Committee, meeting at lunchtimes, to investigate and catalogue all the many possibilities and the intricacies of the new-found art (science?) of flexigation.
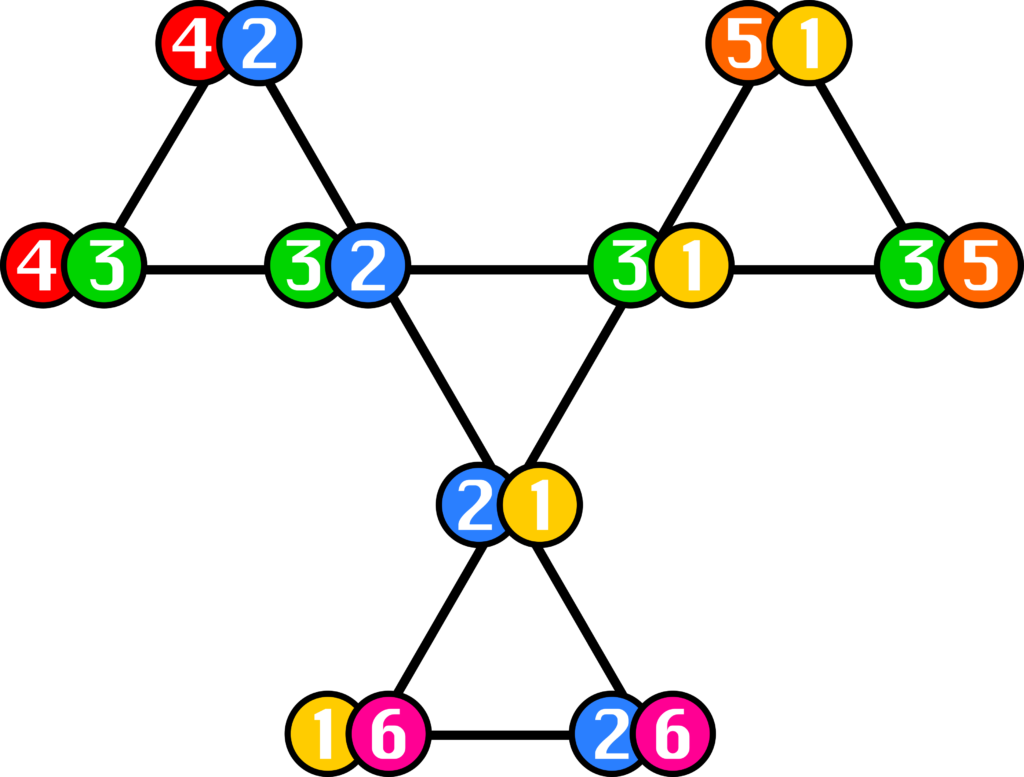 Their discoveries included: a full list of all the possible types of flexagon, and methods for constructing them; a method for finding all six of the faces on a hexahexaflexagon, devised by Stone’s colleague Bryant Tuckerman and called the ‘Tuckerman Traverse’; and a way to describe the possible states of a flexagon, showing which can be reached from which others by flexing, using a graph to illustrate the connections. The graph here shows the hexahexaflexagon’s pairs of faces, and the Tuckerman traverse involves moving all the way around the outside of this graph, visiting every state.
Their discoveries included: a full list of all the possible types of flexagon, and methods for constructing them; a method for finding all six of the faces on a hexahexaflexagon, devised by Stone’s colleague Bryant Tuckerman and called the ‘Tuckerman Traverse’; and a way to describe the possible states of a flexagon, showing which can be reached from which others by flexing, using a graph to illustrate the connections. The graph here shows the hexahexaflexagon’s pairs of faces, and the Tuckerman traverse involves moving all the way around the outside of this graph, visiting every state.
The hexaflexagon also has the wonderful property that when flexed, it’s possible to return to the same face of the flexagon but find that the triangles have changed orientation – so a non-symmetrical design on the faces of the triangle will be presented in two or three different forms, with different corners of the triangle in the centre. This can be exploited, with some careful design, to make beautiful designs which work in all configurations.
The theory of mathematical flexigation was developed in 1939, but became much more widely known in 1959, when maths author Martin Gardner published a column about flexagons in Scientific American. Gardner wrote a regular recreational maths column called Mathematical Games, in which he shared mathematical puzzles and diversions, and the flexagon was a hugely popular topic – he received a large variety of correspondence from people who had discovered other ways to make and decorate flexagons, and some funny stories, many of which he shared in subsequently published columns and books. The article was actually his first for Scientific American, and was so popular, it was the reason they asked him to continue with a regular column. A version of Gardner’s original article, including some of the follow-up correspondence, can be read on the MAA website.
 Others have investigated flexagons in their own ways – mathematician and YouTuber Vi Hart has produced a wonderful selection of her classic fast-talking videos on the subject, including an introduction to flexagons, a follow-up going into some of the Flexagon Committee’s achievements, this useful safety video outlining some of the ways improper use of flexagons can lead to flexigatastrophes, and a more recent definitive guide to making a flexagon. The crowning glory of Hart’s collection of flexagon videos has to be the use of tortilla wraps and fillings to make Mexican food flexagons (flex mex, or hexaflexamexagons). And over at Woolly Thoughts’ website of mathematical knitting patterns, you can find knitted and crocheted flexagons (right), with patterns available through Ravelry.
Others have investigated flexagons in their own ways – mathematician and YouTuber Vi Hart has produced a wonderful selection of her classic fast-talking videos on the subject, including an introduction to flexagons, a follow-up going into some of the Flexagon Committee’s achievements, this useful safety video outlining some of the ways improper use of flexagons can lead to flexigatastrophes, and a more recent definitive guide to making a flexagon. The crowning glory of Hart’s collection of flexagon videos has to be the use of tortilla wraps and fillings to make Mexican food flexagons (flex mex, or hexaflexamexagons). And over at Woolly Thoughts’ website of mathematical knitting patterns, you can find knitted and crocheted flexagons (right), with patterns available through Ravelry.
Finally, if you’d like to make a tri-hexaflexagon with your face on it (and who wouldn’t), my friend Christian has put together an online gadget which will use your phone camera or webcam to take a picture, split your photo onto the correct subset of triangles, and produce a PDF which can then be downloaded, printed, assembled and flexed.
I look forward to receiving all your correspondence on the topic, as Martin Gardner did after his original article – although postcards with more than two sides are difficult to fit in the mail, so maybe just use the comments box below…




Just to the colours:
Vibrant colours means that the printed colors are “vibrant” because of the surface of the paper. Photo paper has very special surface to get very vibrant colors.
Not all papers have the same surface on both sides, especially photo papers have only on one side their high quality surface.
Not the topic here I know, just a minor point.