Few tile attempts

We’ve recently started renovating our bathroom: it needed a refresh, and we’re taking the opportunity to get some new features installed. As part of the work, we’ll be having an entirely new tiled floor, which means an exciting opportunity has presented itself – to put some more mathematics into our home decor!
Tessellation Station

Tilings, also known in maths as tessellations, come in many different types. As well as tilings made entirely using the same repeated shape (called a regular tiling if the shape in question is a regular polygon, like a square) you can also have semiregular, or uniform tilings – with two or more different regular polygons, meeting in different ways to create a repeating pattern.
Sadly if you restrict yourself to regular tilings, your options (for a 2D wall at least) are quite limited – you can only have squares, hexagons or equilateral triangles. None of the other regular polygons are capable of tiling the 2-dimensional plane, and if you want more variety you’re forced to mix and match your shapes.

Uniform tilings have an additional property that every vertex – corner where tiles meet – is the same. Even with two or more shapes, it’s possible to have this condition, and there are several ways to combine equilateral triangles, squares and hexagons, and even dodecagons, to form such a tiling.
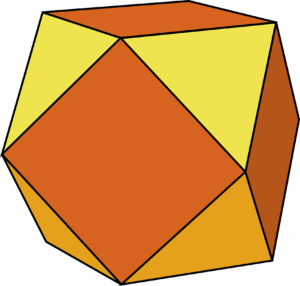
Such tilings are sometimes also called Archimedean tilings, by analogy with Archimedean solids: ones made up of different types of shape, but with each vertex looking the same, like the cuboctahedron pictured here.

Other uniform tilings, called k-uniform, have k different types of vertex, and there are many hundreds of different examples of such tilings. They’re always made using two or more different shapes, with the sizes chosen so that the lengths of the edges all match up to form tilings.
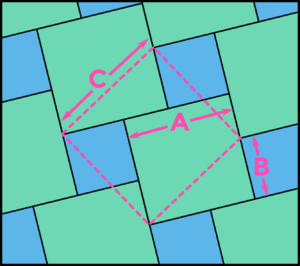
The exception to this is if you relax the requirement that tiles meet at corners – if you’re not bothered about this, you can make non-edge-to-edge tilings, like the Pythagorean tiling. It’s made from two different sizes of square, and is so-called because the relative sizes of the two squares match the lengths of two sides of a right-angled triangle. The tiling itself contains a proof of Pythagoras’ theorem: if the two squares have side lengths A and B, the two shorter edges of the triangle, C is the hypotenuse, and you can see that A² + B² = C² by rearranging the pieces into whole squares.

You can’t tile a plane with regular pentagons, but you can if you’re prepared to use non-regular ones, and as recently as 2015 a new way of tiling the plane using similar pentagons was discovered, bringing the total number of ways known up to 15.
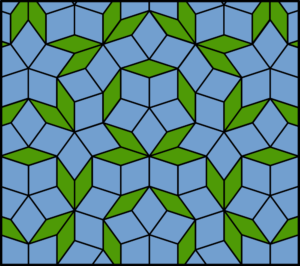
And if you don’t like your tilings to have a repeated pattern, you can always use an aperiodic tiling – one which is made up of the same shape or set of shapes, but doesn’t have a repeating unit and can go on forever without ever repeating the same way. The most famous example is the Penrose Tiling, named after mathematician Roger Penrose, and it consists of two shapes which can fit together but can also tile the whole infinite plane without making a repeating pattern.
Domino dancing

If you allow your square tiles to be non-regular, you can have rectangular tiles, and if they happen to be twice as wide as they are tall, you can make domino tilings. These are ways to arrange tiles measuring 2 by 1 units, and for an n × m rectangle you need (n × m)/2 tiles.

Not all shapes can be tiled in this way – a famous puzzle considers a chessboard, which has been ‘mutilated’, so that the top left and bottom right corners have been cut off. It’s asked if it’s possible to tile such a chessboard with dominoes. I won’t tell you the answer, but you might want to consider what colour the two squares that have been cut off were, and what colour squares a domino on a chessboard will cover up…
So some shapes can’t be tiled, but others can – and any rectangle whose sides aren’t both odd can be covered (if both sides have an odd length, the total number of squares will be odd, so it’s not possible with a whole number of dominoes). But if it is possible, how many ways can it be done?
 To start with, consider a 2 × n rectangle, and count how many ways you can arrange tiles to fill it. For n=0, there’s only one way to fill the rectangle (you don’t). For a 2 × 1 rectangle, you just need one domino, and there’s only one way to put it in; for 2 × 2, you can arrange the two dominoes vertically or horizontally. If you carry on with this, you might see an interesting pattern start to form in the number of possible tilings…
To start with, consider a 2 × n rectangle, and count how many ways you can arrange tiles to fill it. For n=0, there’s only one way to fill the rectangle (you don’t). For a 2 × 1 rectangle, you just need one domino, and there’s only one way to put it in; for 2 × 2, you can arrange the two dominoes vertically or horizontally. If you carry on with this, you might see an interesting pattern start to form in the number of possible tilings…
My bathroom floor is sadly more than 2 tiles wide, so I’ll need to consider the general case – luckily, it was proven twice, by two separate mathematicians in 1961, that for such an (n × m) rectangle there are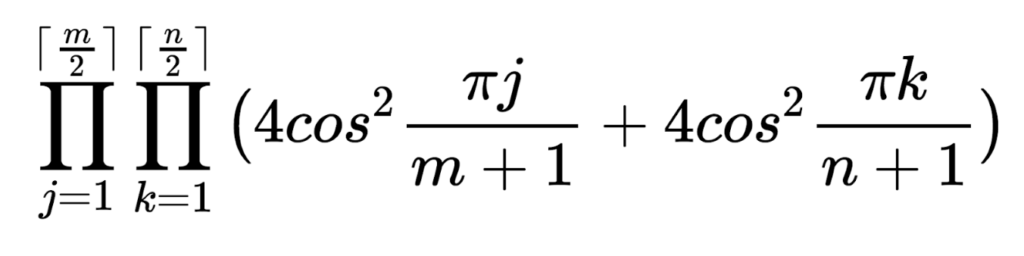 different ways to arrange the tiles. If I’m going to narrow it down to one, I’ll need to put some constraints on.
different ways to arrange the tiles. If I’m going to narrow it down to one, I’ll need to put some constraints on.
Tiling with rules

In Japan, tatami are rectangular floor tiles in this 2 by 1 shape, which are often used to create floors by arranging them in a tiled pattern. Interestingly, it’s considered bad luck (‘inauspicious’) to place the tatami so that four meet at a corner, and they must therefore be arranged so that only three mats meet at any given corner. For rooms with odd sides, half-tatami can be used in the corner, and the sizes of rooms are sometimes given in terms of how many tatami they are tiled with – in parts of Japan, shops are traditionally 5½ tatami along the edge, and tea rooms are 4½.
Another condition you can place on domino tilings is that they can be ‘fault-free’ – a fault is a line all the way across the shape which no tiles cross, so that in theory the tiling could be split into two pieces along this line, like a tectonic fault line. In 1981, Ron Graham worked out the conditions required for an n × m rectangle to have a fault-free tiling by dominoes – an m × n rectangle of area greater than 2 has a fault-free tiling if and only if (m × n) is even, m and n are both 5 or bigger, and m and n do not both equal 6.
 Specifically, it’s not possible to tile a 6 × 6 square using 36 ÷ 2 = 18 dominoes. A proof of this goes as follows: if you want no faults, each of the 10 lines running across or down the middle of the grid between cells must have dominoes that straddle it. Since the square has 6×6 cells, any such line will divide it into two halves containing an even number of cells, which means there must be an even number of dominoes cut in half by each line, otherwise you’d end up with an odd number of squares on one side. Zero is even, but if any of these lines cuts 0 dominoes in half, it’d be a fault – so each of the 10 lines has to cut at least two dominoes. Therefore you need the tiling to contain at least 20 dominoes. This can’t happen, as the square isn’t big enough! QED.
Specifically, it’s not possible to tile a 6 × 6 square using 36 ÷ 2 = 18 dominoes. A proof of this goes as follows: if you want no faults, each of the 10 lines running across or down the middle of the grid between cells must have dominoes that straddle it. Since the square has 6×6 cells, any such line will divide it into two halves containing an even number of cells, which means there must be an even number of dominoes cut in half by each line, otherwise you’d end up with an odd number of squares on one side. Zero is even, but if any of these lines cuts 0 dominoes in half, it’d be a fault – so each of the 10 lines has to cut at least two dominoes. Therefore you need the tiling to contain at least 20 dominoes. This can’t happen, as the square isn’t big enough! QED.
Elephant in the bathroom
Unfortunately for me, as exciting as all these tilings are, not many of them will really work for our bathroom floor. I can probably find square tiles in the tile shop, probably some rectangles and if I’m really lucky maybe some hexagons. But all these other tilings are probably not possible using simple tiling techniques (and our decorator gets a bit angry if you start to suggest the idea of cutting unconventional shapes out of regular tiles, or insisting you lay the tiles in strange layouts). So we needed to come up with something that would work without requiring funky shaped tiles or layouts, but that still has an interesting mathematical twist.
One option we can use to make it more interesting is to colour the tiles – they sell square tiles in a range of colours, so we could use them to create some kind of interesting pattern in colour rather than shape. Our decorator is happy with normal square tiles laid according to a particular colour layout, so we just need to give him a piece of paper with a pattern to follow.
As we already have previous experience of this (see: my Aperiodical post from 2015), we decided to use black and white square tiles to spell out a message in binary, using five tiles for a letter of the alphabet given by a number between 1 and 26.
I won’t give away the message we’ve encoded in the bathroom, but if you keep an eye on my Twitter feed I might post some photos of it once it’s finished!



