Wenn es um die Beziehungen zwischen Mathematik und Musik geht, kommt unweigerlich die Rede auf die Entdeckung, die den Pythagoräern der Antike zugeschrieben wird: dass nämlich zwei gleichartige, gleich gespannte Saiten dann besonders angenehm („harmonisch“) zusammenklingen, wenn ihre Längen in einem einfachen Verhältnis zueinander stehen. Soll heißen: wenn das Verhältnis ihrer Längen durch einen Bruch mit kleinen Zahlen im Zähler und im Nenner ausgedrückt werden kann.

Die Philosophie, die die Pythagoräer damit verknüpften („Alles ist Zahl“), ist heute etwas aus der Mode gekommen – es gibt einfach zu viele bedeutende Beziehungen, die sich nur mit krummen Zahlen beschreiben lassen –, aber der Befund hat standgehalten. Wir drücken die Sache heute lieber in Frequenzen aus statt in Saitenlängen (wodurch wir auch Blas- und andere Instrumente einschließlich der menschlichen Stimme einbeziehen), aber das macht nichts, denn das eine ist dem anderen umgekehrt proportional. Wenn sich die Saitenlängen verhalten wie 2 zu 3, dann verhalten sich ihre Schwingungsfrequenzen wie 3 zu 2, und es erklingt das Intervall, das man eine Quint nennt.

Eine Oktav entspricht einem Frequenzverhältnis von 2 zu 1, eine Quart entspricht 4 zu 3 und eine große Terz 5 zu 4. Mit diesen wahrlich einfachen Brüchen haben wir bereits einen Dur-Dreiklang beisammen und damit das zentrale harmonische Element der uns geläufigen (westlichen) Musik. Das Verhältnis von 2 zu 1 klingt in unseren Ohren so „rein“ wie klares Wasser, weswegen man Töne, die sich nur um eine Oktav unterscheiden, als im Wesentlichen gleich auffasst.

Das ist ein Punkt, den unsere Musiktradition anderen voraus hat: eine physikalische Begründung für die bevorzugten Harmonien. Was sagt uns das? Nicht allzuviel. Die Traditionen anderer Kulturen lehren uns, dass man auch mit ganz anderen Intervallen Musik machen kann. Es ist vermutlich keine gute Idee, aus der Physik die Überlegenheit der westlichen Musik (und dann vielleicht auch gleich der westlichen Kultur) herzuleiten.

Zu allem Überfluss genehmigt sich unsere eigene Musiktradition eine deutliche Abweichung vom pythagoräischen Reinheitsgebot. Türmt man zwölf Quinten aufeinander, so landet man ungefähr bei sieben Oktaven. Aber eben nur ungefähr. Zwölf Quinten sind ein Frequenzverhältnis von (3/2)¹², und das ist um knapp 1,4 Prozent mehr als die 2⁷, die den sieben Oktaven entsprechen. Damit das trotzdem hinkommt, macht man alle Quinten ein bisschen zu klein – Frequenzverhältnis 2^7/12=1,498 statt 1,5 – und gewinnt eine Struktur von einer solchen Reichhaltigkeit, dass man sie nicht missen möchte. Man hat das, was man heute die chromatische Tonleiter nennt: Zwölf gleich große Intervalle („Halbtöne“) ergeben zusammen eine Oktav, und auf jedem dieser zwölf Töne kann man einen Dreiklang aufbauen.

Der Halbtonzirkel und der Quintenzirkel

Wenn man als Grundton wie üblich das C nimmt, führt der letzte Halbtonschritt auf das hohe C, was „im Wesentlichen dasselbe“ ist wie der Grundton. Daher ist es naheliegend, die zwölf Töne der chromatischen Leiter im Kreis anzuordnen:

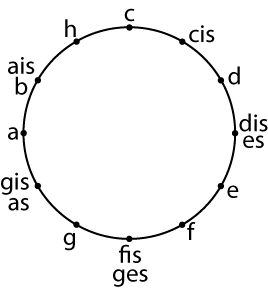
In der heute vorherrschenden gleichschwebend temperierten Stimmung – alle Halbtonschritte sind gleich lang – sind die Töne tatsächlich alle „gleichberechtigt“. Traditionell sind allerdings einige Töne „gleicher“ als andere; die „minderwertigen“ entsprechen den schwarzen Tasten auf dem Klavier. Während die „weißen“ Töne ausgehend vom C durch fortgesetztes Quintenbilden erzeugt werden, haben die „schwarzen“ zwei konkurrierende Erzeugungsweisen und müssen entsprechend mit jeweils zwei Namen leben. So die Theorie von der reinen Stimmung. Die allerdings verteilt den unvermeidlichen „Schmutz“ sehr ungerecht zum größten Teil auf ein paar „schwarze“ Quinten, mit dem Effekt, dass Tonarten wie H-dur oder Des-dur sehr schräg klingen. Zur Abmilderung gab es verschiedene „temperierte“ Stimmungen, von denen unsere gleichschwebend temperierte nur den konsequentesten Extremfall darstellt. An dem Exponat „Scale Lab“ in der Ausstellung „La La Lab“ oder hier im Internet können Sie unter anderem den Effekt verschiedener Stimmungen erproben.

Wer sich bei dieser Grafik an das Zifferblatt einer Uhr erinnert fühlt, liegt genau richtig! Wir pflegen Uhrzeiten „modulo 12 Stunden“ zu benennen, das heißt bei der Zählung der Stunden Vielfache von 12 zu subtrahieren oder zu addieren derart, dass am Ende eine Zahl zwischen 0 und 11 herauskommt. Und die Zahlen, mit denen man rechnet, haben eine doppelte Bedeutung: einerseits als Uhrzeiten, sozusagen fest markierte Punkte auf der Zeitachse, andererseits als Zeitintervall. 8 Uhr plus 5 Stunden ist 1 Uhr, 10 Uhr plus 8 Stunden ist 6 Uhr, und wir legen uns nicht darauf fest, ob die erste Zeitangabe vor- oder nachmittags zu verstehen ist.

Entsprechend steht ein Punkt in dem oben gezeigten „Halbtonzirkel“ einerseits für einen Ton, sagen wir eine Taste auf dem Klavier plus alle ihre Kolleginnen, die um eine oder mehrere Oktaven höher oder tiefer liegen; andererseits für ein musikalisches Intervall, das heißt eine gewisse Anzahl von Halbtonschritten. Wenn man den Halbtonzirkel mit denselben Nummern versieht wie das Zifferblatt einer Uhr (vielleicht ganz oben mit 0 statt 12, aber das ist Geschmackssache), dann ist die Vier einerseits der Ton E, andererseits die große Terz.

Die Mathematiker nennen eine solche Struktur „die additive Gruppe modulo 12“. Gruppen sind ein zentrales Objekt der Algebra, es gibt einen ganzen, äußerst unübersichtlichen Zoo von Gruppen, und unsere Uhrzeiten- bzw. Halbtönegruppe ist eines der einfachsten Exemplare. Sie ist zyklisch, das heißt man kann ihre Elemente sinnvoll in einem Kreis anordnen. Und das kommt daher, dass ein einziges Element – die Zahl 1, das Zeitintervall eine Stunde, der Halbtonschritt – die ganze Gruppe „erzeugt“. Das wiederum heißt: Wenn man die Null – das „neutrale Element“ – nimmt und das erzeugende Element immer wieder dazuaddiert, erhält man auf die Dauer alle Elemente der Gruppe.

Eine zyklische Gruppe hat im Allgemeinen nicht nur ein erzeugendes Element. Bei der additiven Gruppe modulo 12 erfüllt zum Beispiel auch die Sieben diese Rolle, und das hat nun auch musikalische Bedeutung. Mit der Sieben wird nämlich aus dem Halbtonzirkel der Quintenzirkel:

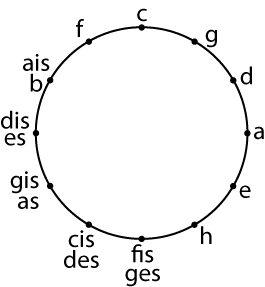
Wenn man den Quintenzirkel in der Halbtönedarstellung einzeichnet, also zwei Töne miteinander verbindet, wenn sie genau um eine Quinte auseinanderliegen, sieht das ziemlich unübersichtlich aus. Und der Folge der Halbtöne geht es in der Quintenzirkeldarstellung nicht besser:

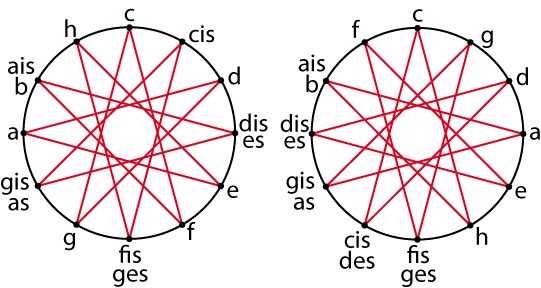
Mathematisch sind beide Darstellungen der Gruppe völlig gleichberechtigt.

Das Tonnetz und der Tönetorus

Wie sieht nun das zentrale musikalische Objekt, der Dreiklang, in dieser oder der anderen zyklischen Darstellung aus? Na ja, ein Dreieck halt, unregelmäßig auf jeden Fall, irgendwie halbspitz in der Halbtondarstellung, sehr spitz in der Quintenzirkeldarstellung. Immerhin sehen die Dreiklänge alle gleich aus, je nach Tonart etwas gedreht, und Moll (blau) ist das Spiegelbild von Dur (rot).

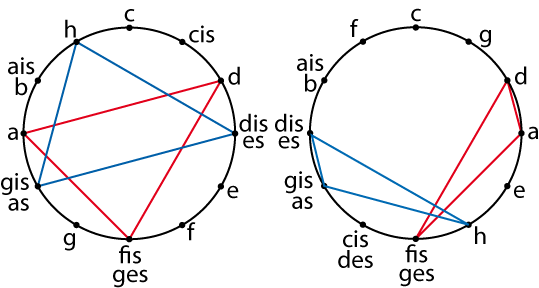
Das Programm Tonnetz aus der Ausstellung La La Lab zeigt Ihnen diese Dreiecke, wenn Sie in den entsprechenden Dreiklang klicken. Aber besonders eindrucksvoll ist das nicht. Es sind halt nur irgendwelche Dreiecke, was der herausgehobenen Rolle der Dreiklänge nicht entspricht.

Abhilfe findet sich auf derselben Website. Ein Weg, sich dieser „Tonnetz“- Darstellung zu nähern, verwendet das Konzept vom Koordinatensystem. Nullpunkt ist – zum Beispiel – das C. Auf der x-Achse trägt man die Quinten ab und auf der y-Achse die (großen) Terzen. Dann kann man jeden der zwölf Töne dadurch beschreiben, wie viele Quint- und wie viele Terzschritte man gehen muss, um vom C zu ihm zu gelangen.

An dieser Stelle wird dem echten Gruppentheoretiker unwohl. Ja, es gibt Gruppen, für die ein solches Koordinatensystem eine angemessene Beschreibung ist, allen voran die additive Gruppe der Paare aus zwei ganzen Zahlen. Aber unsere Gruppe der zwölf Halbtöne! Vom Standpunkt des Puristen aus ist die y-Achse schlicht entbehrlich; auf der x-Achse liegen ja schon sämtliche Elemente. Zu allem Überfluss ist die x-Achse keine schöne Gerade, sondern zum Kreis gebogen; die Zwölf ist ja schon wieder identisch mit der Null. Und die Terzen-Achse ist noch viel krummer! Drei große Terzen geben ja schon eine Oktav.

Man hat also ein Rechteck, bei dem die linke (x=0) und die rechte Seite (x=12) eigentlich dasselbe sind, desgleichen für die untere (y=0) und die obere Seite (y=3). Dafür gibt es ein bewährtes Verfahren: Man rolle das Rechteck zunächst zu einer zylindrischen Röhre, indem man untere und obere Seite miteinander verklebt. Dann muss man sich das ganze Material sehr dehnbar vorstellen, denn jetzt krümmt man den ganzen Zylinder kreisförmig und verklebt das eine Ende mit dem anderen. Das Endergebnis ist ein Torus, besser bekannt als Donut oder – für die Süßigkeitenverächter – als Fahrradschlauch.

Wer die Achsen nicht krümmen will, muss in Kauf nehmen, dass alle Töne, wie in der Tonnetz-Darstellung, mehrfach vorkommen. Schlimmer noch: Selbst unser Torus enthält noch reichlich Doubletten. Immerhin sind vier Quinten (bis auf die zwei Oktaven) dasselbe wie eine große Terz, oder in Zahlen: 4 ^. 7 modulo 12 = 28 modulo 12 = 4.

An dieser Stelle haben sogar die Pythagoräer ein Problem: Vier Quinten sind 81/16 beziehungsweise 81/64, nachdem man die zwei Oktaven herausgerechnet hat. Dagegen ist eine reine Großterz 5/4=80/64, und das Vierundsechzigstel Unterschied kann man hören, wenn man sich etwas Mühe gibt. Deswegen gibt es einen Unterschied zwischen einer „pythagoräischen“ und einer „reinen“ Stimmung, und die „schmuddelige“ gleichschwebend temperierte Terz (1,25992) ist näher an der reinen (1,25) als die pythagoräsche (1,26563).

Was tut man, wenn man der – durchaus vernünftigen – Forderung folgen will, dass jeder Ton nur einmal in dem Schema vorkommt? Man schneidet das Rechteck nicht erst bei x=12, sondern schon bei x=4 ab:

Die obere und die untere Seite miteinander zum Zylinder zu verkleben funktioniert wie zuvor. Aber um die rechte mit der linken zu verbinden, muss man die Zylinderröhre irgendwie in sich verwinden, damit c auf c, e auf e und gis/as auf gis/as zu liegen kommt. So ähnlich wie man ein Möbiusband zusammenklebt, bloß mit einer Drittel- statt einer Halbdrehung. Ja, dafür muss das Material wieder sehr dehnbar sein.

Dieser verwundene Torus ist die mathematisch saubere Darstellung der Dreiklangsstruktur der zwölf Töne unserer chromatischen Tonleiter. Leider ist er so unansehnlich, dass er als Mittel der Erkenntnis eher ungeeignet ist.

Was tun? Der einfachste Weg ist, den Torus gar nicht erst aufzuwickeln, sondern das Tonnetz in der Ebene aufzuspannen. Dabei nimmt man in Kauf, dass alle Elemente mehrfach auftreten, theoretisch sogar unendlich oft.

Ein anderer Kompromiss: Man verklebe zwar oben und unten, aber nicht rechts und links, stelle den entstehenden, nach wie vor verwundenen Zylinder hochkant, ersetze die (krummen) Linien, die die Töne miteinander verbinden, durch gerade und richte die Verwindung genau so ein, dass diese Verbindungslinien alle gleich lang sind. Das geht! Das Ergebnis ist ein Stapel aus vier regelmäßigen Oktaedern. Jede Ecke des Stapels entspricht einem Ton und jede der Dreiecksflächen einem Dur- oder Moll-Dreiklang. Im „Erlebnisland Mathematik“ in Dresden kann man ein solches Dreiklangpolyeder besichtigen – und erklingen lassen. Nur dass die Deckfläche „eigentlich“ dasselbe ist wie die verdrehte Grundfläche, muss man sich dazudenken.

Durch dieses Exponat motiviert, habe ich versucht, das eckige Gebilde zum Torus zu schließen. Es geht, sieht aber ziemlich hässlich aus. Wenn man dagegen zwei Dreiklangpolyeder aufeinandersetzt und das Ganze zum Torus krümmt, ist das Ergebnis einigermaßen ansehnlich.

Ich habe meine Bastelei den „Möbiusschen Quintenzirkel“ genannt – nicht nur, weil die Oberfläche so ähnlich gewunden ist wie ein Möbiusband, sondern weil demselben August Ferdinand Möbius (1790–1868) auch die Idee mit den gestapelten Oktaedern zugeschrieben wird.

Was kann nun ein Musiker mit dem mehr oder weniger aufgewickelten Tonnetz anfangen? Einiges. Jedes Dreieck im Netz ist ein Dreiklang, Dur und Moll wechseln sich ab, und in einem üblichen Musikstück wandern die Harmonien in der Regel in kleinen Schritten auf dem Tonnetz umher. Von Dur zur gleichnamigen Molltonart geht es über eine einzige Kante, ebenso zur parallelen Molltonart (derjenigen mit denselben Vorzeichen). Die häufigsten Übergänge, Tonika zu Dominante oder Subdominante und zurück, gehen von einem Dreieck zu einem über Eck benachbarten. Eine ähnlich kurze Entfernung besteht zur „terzverwandten“ Tonart, zum Beispiel von C-dur nach As-dur oder E-dur, ein Übergang, den vor allem die Komponisten der Romantik für manchen Überraschungseffekt nutzten.

Hat unsere Zwölfergruppe weitere erzeugende Elemente? Nicht wirklich. Wenn ein Gruppenelement mit der Zwölf einen gemeinsamen Teiler hat, dann landet man beim Immer-wieder-Aufaddieren bei einem Vielfachen von 12 und damit bei der Null, bevor man alle Elemente abgegrast hat. Das gibt dann eine Untergruppe, also eine Teilmenge, die ihrerseits wieder Gruppenstruktur hat.

So erzeugt die Drei die Untergruppe {0, 3, 6, 9} oder auch {c, es, fis, a}: Immerhin – das kennt man in der Musik als den verminderten Septakkord. Aber die Musiker interessiert an ihm nicht seine Eigenschaft als Untergruppe, sondern dass er als Dissonanz empfunden wird, obgleich er aus lauter konsonanten kleinen Terzen besteht. Traditionell dient er zum Ausdruck höchster Erregung – eindrucksvoll, wie Beethoven ihn zum Beginn des Finales seiner Appassionata ins Klavier hämmert.

Die Untergruppe, die von der Vier (der großen Terz) erzeugt wird, findet bei den Klassikern nur selten Verwendung; aber die Impressionisten schätzten die schwebende Unbestimmtheit eines Klanges wie {c, e, gis} aus drei großen Terzen.

An erzeugenden Elementen bleiben neben der Eins (Halbtonzirkel) und der Sieben (Quintenzirkel) nur noch die Fünf und die Elf. Und die bringen nichts Neues. Die Fünf erzeugt den Quintenzirkel rückwärts, denn 5=–7 modulo 12. Und da 11=–1 modulo 12 ist, liefert sie nichts weiter als die chromatische Tonleiter abwärts.

Und damit ist der kurze Flirt zwischen Harmonik und Gruppentheorie schon wieder zu Ende. Ja, es gibt mathematisch fassbare Strukturen, gerade in den Harmonien. Aber – sagen wir es metaphorisch: Das ist nicht unbedingt da, wo die Musik spielt.