Der Spiegel
BLOG: Heidelberg Laureate Forum

Das Gesicht, das Sie morgens über dem Waschtisch anschaut, das sind Sie selbst. Oder? Falsch. Wie jeder Ihrer Mitmenschen Ihnen bestätigen kann, sind Ihr Anblick im Original und im Spiegelbild ziemlich verschiedene Dinge. Jeder kennt Spiegel, und trotzdem sind sie irgendwie seltsam – was man seit dem 12. Februar in Heidelberg in der Ausstellung „Faszination Spiegelwelten“ bewundern kann.
Besonders ungewohnt wird es, wenn die verspiegelte Fläche krumm ist. Da schaut man auf die Spitze eines verspiegelten Kegels und findet eine ganz normale Szene vor. Auf dem Papier, auf dem der Kegel steht, findet sich jedoch eine merkwürdig kryptische Zeichnung. Erst auf den dritten Blick wird man gewahr, dass sie genau das Bild zeigt, das man über den Kegelspiegel sieht, nur eben grotesk verzerrt.

Ein Kleeblatt: Anamorphose mit Kegel in der MAINS Ausstellung „Faszination Spiegelwelten“
Ähnliches funktioniert, wenn der Spiegel die Form eines Zylinders statt eines Kegels hat. Die dafür gefertigten Zerrbilder heißen „Anamorphosen“ und haben eine lange Tradition in der bildenden Kunst.
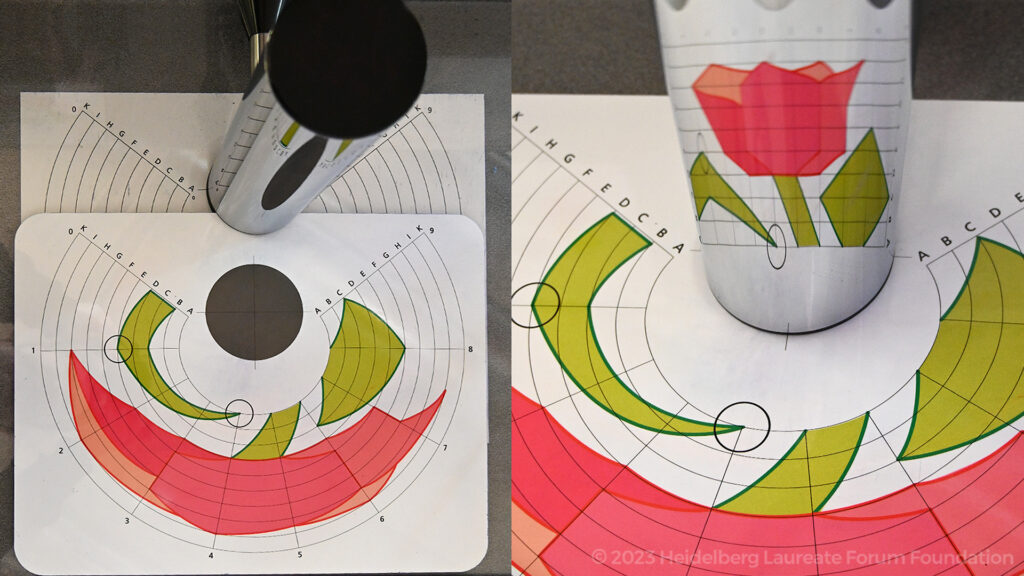
Eine Tulpe: Anamorphose mit Zylinder in der MAINS Ausstellung „Faszination Spiegelwelten“
Und wer vor einem Spiegel in Wellenform steht, sieht sich als dicker Gartenzwerg, als Bohnenstange oder als merkwürdige Mischung. Da stehen Ihnen die Haare zu Berge und vereinigen sich vielleicht sogar mit den Haaren Ihres kopfstehenden Doppelgängers.

Der „Zerr-/Wellenspiegel“ in der MAINS Ausstellung „Faszination Spiegelwelten“
Was die Lichtstrahlen alles anstellen auf dem Weg zum Spiegel und zurück, kann man natürlich auch nachrechnen. Das schlichte physikalische Gesetz „Einfallswinkel gleich Ausfallswinkel“ ist eigentlich alles, was man dazu braucht. Gemessen werden beide Winkel gegen die Senkrechte auf die Spiegelebene (das „Einfallslot“), und wo der Spiegel nicht eben ist, muss man in dem Punkt, wo der Lichtstrahl auftrifft, ersatzweise eine gedachte Ebene verwenden, die in diesem Punkt der krummen Fläche des Spiegels am nächsten kommt: die Tangentialebene. Ohne größeren Aufwand entdeckt man dann, dass ein Hohlspiegel dazu neigt, die eintreffenden Lichtstrahlen auf engem Raum zu konzentrieren, weswegen er in Scheinwerfern und Teleskopen Verwendung findet, während ein Konvexspiegel, also einer, der mir seinen dicken Bauch entgegenstreckt, das Licht eher zerstreut.
Und wenn die Spiegel alle eben sind? Dann gibt es keine Verzerrungen. Vielmehr sind Längen und Winkel im Spiegelbild genau so groß wie im Original. In der Sprache der Schulgeometrie: Original und Bild sind kongruent, die Spiegelung ist eine Kongruenzabbildung. Mit der kleinen Besonderheit, dass das Bild irgendwie „andersrum“ ist als das Original.
In diesem Zusammenhang kommt regelmäßig die Frage auf: „Warum vertauscht ein Spiegel rechts und links, aber nicht oben und unten?“ Die Antwort lautet: Er vertauscht gar nicht rechts und links. Vielmehr vertauscht er vorn und hinten. Nur: Wenn Sie vor dem Spiegel stehen, stellen Sie sich den Menschen, der Sie da anblickt, unwillkürlich so vor, als wäre Ihr zweites Ich hinter den Spiegel gewandert und hätte sich unterwegs um 180 Grad gedreht. Dieser gedachte Mensch trüge dann in der Tat den Ehering an der falschen Hand, er wäre Linkshänder, wenn Sie Rechtshänder sind, und wäre überhaupt in jeder Hinsicht seitenverkehrt. Das Spiegelbild einer rechtsdrehenden Spirale ist eine linksdrehende, und so weiter.
Wer gerne in Koordinaten denkt, kann sich den Spiegel in der (y, z)-Ebene eines dreidimensionalen Koordinatensystems vorstellen. Dann macht der Spiegel aus dem Punkt (x, y, z) den Punkt (–x, y, z). Und mit Mitteln der linearen Algebra kann man das noch etwas eleganter ausdrücken. Die Spiegelebene kann irgendwie schräg liegen, wenn nur der Nullpunkt in ihr liegt. Dann ist die Spiegelung an dieser Ebene eine lineare Abbildung mit Determinante –1. (Umgekehrt gilt das nicht! Lineare Abbildungen, selbst solche mit Determinante –1, können im Allgemeinen allerlei anstellen, was mit Spiegelung nicht mehr viel zu tun hat.)
Ein Gegenstand wird durch eine Spiegelung falschrum, und wenn dieses Spiegelbild nochmals gespiegelt wird, ist er wieder richtigrum. Die Regel „minus mal minus gibt plus“ gilt nämlich auch für Determinanten von Matrizen. Genauer: Zwei Spiegelungen an verschiedenen Ebenen sind dasselbe wie eine Drehung um die Gerade, die beiden Ebenen gemeinsam ist. Der Winkel der Drehung ist das Doppelte des Winkels, unter dem die Ebenen sich schneiden. Und bekanntlich ändert eine Drehung nichts an der Orientierung (richtigrum oder falschrum) des gedrehten Objekts.
Und wenn die Ebenen sich gar nicht schneiden, sondern parallel sind? Dann ist die doppelte Spiegelung nichts weiter als eine Parallelverschiebung, und zwar um zweimal den Vektor, der auf beiden Ebenen senkrecht steht und von der einen zur anderen weist. Das ist mit Matrizen allein zwar nicht mehr auszudrücken – schließlich können nicht beide Spiegelebenen zugleich durch den Nullpunkt gehen – aber die lineare Algebra stellt auch dafür die Mittel bereit.
Spiegelung, Drehung, Parallelverschiebung: Das ist bereits das vollständige Sortiment der Kongruenzabbildungen. Also kann man jede Abbildung, die Längen und Winkel unverändert lässt, aus Spiegelungen zusammensetzen. In der Tat haben manche Mathematiker die komplette Geometrie aus dem Spiegelungsbegriff aufgebaut. Damit rückt die Frage in den Mittelpunkt, was im Allgemeinen passiert, wenn man mehrere Spiegelungen hintereinander ausführt.
Wenn man ein und dieselbe Spiegelung zweimal hintereinander anwendet, landet man wieder beim Original. Wenn man sich das mit echten Spiegeln vorstellt, ist das einigermaßen absurd: Herr X steht davor und betrachtet sein Spiegelbild, nennen wir es Herrn Y. Den gibt es zwar nicht, aber wenn er dort hinter dem Spiegel stünde, wo Herr X ihn zu sehen glaubt, dann würde er im Spiegel (die Glasplatte ist von beiden Seiten verspiegelt) Herrn X sehen, und zwar genau dort, wo der real existierende Herr X steht.
Na gut; in der mathematischen Abstraktion ist das alles viel einfacher. Da ist das Spiegelbild so real wie das Original, denn beide gibt es nur in unserer Vorstellung. Und die mathematische Abbildung namens Spiegelung ist ihre eigene Umkehrung.
Nehmen wir jetzt an, wir haben zwei Spiegel und spiegeln erst am ersten, dann am zweiten, dann wieder am ersten und wieder am zweiten. Sind wir dann wieder zurück beim Original? Nein! Wenn die beiden Spiegel parallel sind, sind die ersten beiden Aktionen eine Parallelverschiebung und die letzten beiden dieselbe Parallelverschiebung noch einmal, und zweimal dieselbe Parallelverschiebung anwenden läuft nicht auf Nichtstun hinaus, sondern auf eine Parallelverschiebung mit dem doppelten Vektor. In der nächsten Runde Doppelspiegelung ist es der dreifache Vektor, dann der vierfache und so weiter.
Das können die Kinder in der Ausstellung in spektakulärer Weise erleben, indem sie in den innenverspiegelten „Unendlichkeitswürfel“ kriechen.

Der „Unendlichkeitswürfel“ in der MAINS Ausstellung „Faszination Spiegelwelten“
Und die Eltern können ihnen durch die Aussparungen oben dabei zuschauen.

Der „Unendlichkeitswürfel“ in der MAINS Ausstellung „Faszination Spiegelwelten“
Wiederholte Reflexion an Paaren paralleler Spiegel macht aus einem Kind ganz viele, verschoben mit dem einfachen, doppelten, dreifachen … Vektor. Und wenn nicht bei jeder Reflexion ein kleiner Teil des Lichts verlorenginge, könnte das Kind unendlich viele Bilder seiner selbst besichtigen, und das in allen drei Raumrichtungen und mit beiden Vorzeichen. Unsere beiden Spiegelungen, in umgekehrter Reihenfolge ausgeführt, ergeben eine Parallelverschiebung mit dem negativen Vektor.
Bei nicht-parallelen Spiegeln passiert etwas ganz Ähnliches. Die Vierfachspiegelung läuft auf zwei Drehungen mit demselben Winkel hinaus, also sind wir am Ende deutlich woanders als am Anfang. So wie oben die Verschiebungsvektoren addieren sich hier die Drehwinkel – wenn alle Drehungen um dieselbe Achse erfolgen.
Nur mit den unendlich vielen Spiegelbildern funktioniert das nicht so eindrucksvoll. Irgendwann wachsen die Drehwinkel über die 360 Grad hinaus, und dann mischen sich die neuen Bilder unter die alten, was ziemlich verwirrend aussieht, oder sie fallen mit den alten zusammen, wenn man sich geschickt anstellt, das heißt, einen Drehwinkel wählt, der gleich einem Teiler von 360 Grad ist.
Das kann man in der Ausstellung eigenhändig ausprobieren. Ein Ensemble von vier rautenförmig angeordneten Spiegeln ist mit einer Schnur verbunden, mit deren Hilfe man den Winkel zwischen zwei benachbarten Spiegeln variieren kann. Nur bei ganz bestimmten Stellungen fügen sich die Sternchen, die weiter innen angebracht sind, zu einem regelmäßig kreisförmigen Muster. In jeder anderen Stellung gibt es ein nicht sonderlich attraktives Durcheinander.
Der rautenförmige „Polytakis“ in der MAINS Ausstellung „Faszination Spiegelwelten“
Da die vier Spiegelebenen sich in lauter verschiedenen Geraden treffen, kommen auch Zusammensetzungen von Drehungen um verschiedene Achsen vor. Und da stellt sich heraus, dass es darauf ankommt, in welcher Reihenfolge zwei derartige Drehungen ausgeführt werden. Im Allgemeinen sind die Ergebnisse verschieden, und konkurrierende Vierfachspiegelbilder überlagern sich. Nur bei sehr speziellen Winkeln fallen die Bilder zusammen.
Wenn man jetzt noch ein bisschen weitersucht, nach einer Menge von Spiegelungen und Drehungen mit der Eigenschaft, dass die Zusammensetzung von zwei Abbildungen aus der Menge wieder zur Menge gehört, landet man ganz schnell bei der Gruppentheorie. (Eine Menge, die die genannte Bedingung und noch ein paar mehr erfüllt, nennt man eine Gruppe.) Und wenn alle Spiegelebenen durch den Nullpunkt gehen sollen und deswegen alle Drehungen, die sich aus diesen zusammensetzen lassen, den Nullpunkt unverändert lassen, und außerdem die gesamte Menge endlich sein soll: Dann gibt es gar nicht so viele Gruppen, die all diesen Forderungen genügen. Noch einen Schritt weiter, dann weiß man, warum es nur fünf platonische Körper gibt.
Na gut, das sieht man den Spiegeln nicht so unmittelbar an.


Vier Spiegel und zwei unsichtbare Äpfel, ein Bild:
http://s880616556.online.de/USIGER-4.jpg
Die Überlegungen dazu:
http://s880616556.online.de/UNSIBA-7.jpg
Christoph Pöppe schrieb (22. Feb 2023):
> […] Was die Lichtstrahlen alles anstellen auf dem Weg zum Spiegel und zurück […]
> Das schlichte physikalische Gesetz „Einfallswinkel gleich Ausfallswinkel“
… gibt der Formulierung “… und zurück” allerdings eine eher ungewöhnliche Bedeutungs-Facette; vgl. comment 08.02.2023, 17:17 o’clock.
> Gemessen werden beide Winkel gegen die Senkrechte […] (das „Einfallslot“) […] auf die Tangentialebene.
> […] in dem Punkt, wo der Lichtstrahl auftrifft
Mit dieser Beschreibung verbinden sich (bekanntlich) gewisse Näherungen und Abschätzungen
(z.B. der Ausdehnung der jeweils bestrahlten Region des spiegelnden Materials verglichen mit Entfernungen zu Strahlquelle bzw. -empfänger).
> ersatzweise eine gedachte Ebene verwenden, die in diesem Punkt der krummen Fläche des Spiegels am nächsten kommt: die Tangentialebene.
Jeweils genau einem bestimmten Punkt (“des Raumes”) “am nächsten” “kommt” allerdings offenbar jede denkbare Ebene (bzw. ansonsten geeignet verallgemeinert: jede denkbare Fläche, die aus Raum-Geodäten zusammengesetzt werden kann), die genau diesen Punkt schlicht enthält (und das beinhaltet natürlich zahlreiche verschiedene, “räumlich ungleich orientierte” Ebenen bzw. Flächen).
Auf welche von all diesen Flächen bezieht sich denn nun das „Einfallslot“, das vermeintlich hinsichtlich jeder bestimmten bestrahlten Region des gegebenen spiegelnden Materials eindeutig wäre ?? …
(Worauf ich hier, wie meistens, schließlich hinausmöchte, ist natürlich “das RT-Problem”:
Was kommt zwangsläufig zuerst —
die Feststellung bzw. Festlegung (“bis auf Morphismen”) “des Tangentialraumes” einer in Betracht stehenden Punktmenge; oder
die Feststellung bzw. Festlegung (“bis auf Skalierung”) “des metrischen oder geeignet verallgemeinerten Raumes” dieser Punktmenge
??)
p.s.
Im “anderen Laden”, und in anderem Zusammenhang, liegen weitere Fragen öffentlich vor, die sich auf öffentliche Äußerungen von Christoph Pöppe beziehen.
Vorsicht, deutsche Grammatik! “der krummen Fläche” ist nicht Genitiv, sondern Dativ (sonst kommt der Satzbau überhaupt nicht hin). Wenn ich sage, dass “die Tangentialebene in einem bestimmten Punkt der Fläche am nächsten kommt”, dann ist das die übliche Verkürzung von “in einer Umgebung dieses Punktes, die beliebig klein werden darf, der Fläche am nächsten kommt”. Und was das genau bedeutet, sagt einem die Differenzialrechnung. Die ist aber hier nicht Thema, weswegen ich es bei der Kurzform, die an die Anschauung appelliert, belassen habe.
Was auch immer SIe unter dem RT-Problem verstehen: Es ist hier ebenfalls nicht Thema. Für die Zwecke meines Textes können wir davon ausgehen, dass wir im klassischen euklidischen dreidimensionalen Raum leben und dass unsere Spiegeloberflächen differenzierbare Mannigfaltigkeiten in diesem Raum sind. Real existierende Spiegel sind ausreichend gute Näherungen an diese Idealvorstellung.
Die “weiteren Fragen” beziehen sich auf einen “Spektrum”-Artikel von mir und sollten bitte dort diskutiert werden.
Christoph Pöppe schrieb (24.02.2023, 11:45 o’clock):
> Vorsicht, deutsche Grammatik! […]
Vorsicht vor (allzu) leichtfertigen Mahnungen zur Vorsicht! …
> […] (sonst kommt der Satzbau überhaupt nicht hin).
Wenn man nicht wenigstens unserer schönen deutschen (Korrespondenz-)Sprache Vertrauen entgegenbringen könnte — wem dann ??.
Um all dem aber Konstruktives abzugewinnen, möchte ich etwas Wesentliches, das sicherlich “offensichtlich so gemeint” und “einvernehmlich verstanden” ist, vorsichtshalber einmal ausdrücklich formulieren und abgleichen:
Der im obigen SciLog-Artikel in Betracht gestellte “Punkt, wo der Lichtstrahl auftrifft”
– soll ausdrücklich zur Fläche gehören, die “dem Spiegel” als dessen Oberfläche zugeschrieben wird, sofern eine solche überhaupt eindeutig bestimmt werden kann; und falls so:
– soll ebenfalls ausdrücklich zur Tangentialebene der Spiegel-Oberfläche gehören, sofern eine solche Tangentialebene überhaupt eindeutig bestimmt werden kann.
> Wenn ich sage, dass “die Tangentialebene in einem bestimmten Punkt der Fläche am nächsten kommt”, dann ist das die übliche Verkürzung von “in einer Umgebung dieses Punktes, die beliebig klein werden darf, der Fläche am nächsten kommt”.
Mich wundert nur, warum da schlicht (und in solcher Schlichtheit ME doch eher unüblich) vom “am nächsten Kommen” die Rede ist;
und nicht vom (ME üblicheren) “Berühren bzw. Anschmiegen (anstatt Schneiden)” — als Verkürzung bzw. Jargon für einen Sachverhalt,
der Feststellungen/Bewertungen/Messungen oder Vorstellungen von “Nähe” bzw. von “Abstand” in vergleichsweise mitteilenswertem Zusammenhang erfordern dürfte.
> Und was das genau bedeutet, sagt einem die Differenzialrechnung. Die ist aber hier nicht Thema, […]
Dennoch bleibt zu thematisieren, wie und welche (Differential-)Rechnung jeweils überhaupt aufzustellen wäre, nicht wahr ?.
> Für die Zwecke meines Textes können wir davon ausgehen, dass wir im klassischen euklidischen dreidimensionalen Raum leben
… wer davon auszugehen in der Lage ist, erspart sich immerhin die Beschäftigung mit geeigneten, nicht ebenen Verallgemeinerungen von Tangentialebenen …
> und dass unsere Spiegeloberflächen differenzierbare Mannigfaltigkeiten in diesem Raum sind.
Und das steht kurz für: … Was ??
(Etwa schlicht:
für positiven oder divergierenden, nach unten beschränkten Umkugel-Radius von je vier Punkten der in Betracht gestellten Fläche ? … )
p.s.
> Die “weiteren Fragen” beziehen sich auf einen “Spektrum”-Artikel von mir
Konkret auf die Grafik
Parallelprojektion des Einheitswürfels | Parallelprojektion des Einheitswürfels in fünf Dimensionen auf die Ebene. Es sind zusätzlich sämtliche Kanten des Würfels eingezeichnet.
[ © Christoph Pöppe (Ausschnitt) ]
> und sollten bitte dort diskutiert werden.
Da man immerhin (auch) dort Beiträge einreichen kann, ohne sich dafür anmelden zu müssen, schließe ich mal nicht von vornherein aus, dass ich meine Fragen dazu auch dort noch einreichen werde. Für nennenswerte Diskussion erscheinen mir die SciLogs (bzw. der andere Laden) allemal … vertrauter.
Frank Wappler schrieb (24.02.2023, 17:20 o’clock):
> […] für positiven oder divergierenden, nach unten beschränkten Umkugel-Radius […]
Dass positive Werte “nach unten beschränkt” (oder wohl noch besser und üblicher ausgedrückt: “von unten beschränkt”) sind, nämlich mindestens mit Unterschranke Null, ist ja ganz selbstverständlich. Meine beabsichtigte Forderung war vielmehr:
Interessant ist auch, dass die Reflektion an einer Metalloberfläche das Licht anders beeinflusst, als die Totalreflektion an einer Glas-Luft-Oberfläche.
Wenn man nun auf eine totalreflektierende Glas-Luft-Oberfläche eine dünne Metallschicht aufbringt, dann kann man das für die Oberflächenplasmonenresonanzspektroskopie verwenden.
https://upload.wikimedia.org/wikipedia/commons/d/d5/Surface_Plasmon_Resonance_%28SPR%29.jpg
Nachtrag:
Das abgebildete Experiment findet in wässriger Lösung statt, und nicht in Luft.
Zweiter Nachtrag:
Ein stark vereinfachtes Bild der Unterschiede
zwischen Metallreflektion und Totalreflektion.
Die durch die Interferenz unterdrückte Energie
geht dann in die Oberflächenplasmonen.
Das Biacore-System ist ein Gerät, das so arbeitet.
http://s880616556.online.de/INTERLO2.png
Die zweite Unsichtbarkeit:
Ein optischer Oberflächenspiegel und zwei halbe Zylinderlinsen.
Die halben Zylinderlinsen sind konfokal angeordnet, und ihre
gemeinsamen Brennlinien liegen auf dem Oberflächenspiegel,
im Spalt unter dem mittleren, von vorne unsichtbaren Bild.
http://s880616556.online.de/UNSZYL-1.jpg
Nach diesem Prinzip:
http://s880616556.online.de/UNFRZYL4.PNG
Wie man nur mit Spiegeln einen Gegenstand unsichtbar macht, und allerlei andere Spiele mit Spiegeln hat Norbert Treitz in den “Physikalischen Unterhaltungen” in “Spektrum der Wissenschaft” beschrieben: Juni 2004, S. 102 und Januar 2010, S. 42. (Wieso ich das jetzt noch weiß? Ich war der zuständige Redakteur.)
Hallo Herr Pöppe,
im August 2004 habe ich dann im Spektrum der Wissenschaft
auf Seite 8 diesen Leserbrief mit zwei Bildern eingebracht:
http://s880616556.online.de/USIBSPEK.pdf
Jemanden aktuell um 180 Grad zu drehen ist eine ziemlich harmlose Operation. Eine echte Spiegelung hingegen scheint mir eher fatal zu sein. Mich gruselt es bereits bei der Vorstellung.
Wenn man darüber nachdenkt, was wir sehen, dann wird es in der Tat seltsam.
Also , eine Lochkamera vertauscht rechts und links und auch oben und unten.
Unsere Augenlinse vertauscht rechts und links und auch oben und unten.
Unser Gehirn korrigiert das oben und unten, aber das rechts und links nicht ???
… warum vertauscht der Spiegel oben und unten nicht ?
Hallo Herr senf,
wenn man den Spiegel an der Decke montiert,
dann vertauscht der Spiegel oben und unten.
Das erkennende Subjekt erfasst seine Umwelt, also die Welt(lichkeit), ausschnittsartig, näherungsweise und an Interessen gebunden (!), philosophisch ist dies klar; insofern stellt der Spiegel, wie auch jede andere Ansicht eines Menschen, eine per Instrument erfasste Datenprobe oder Sicht dar, die das Visuelle meint, versus ‘Das sind Sie selbst!’
Dr. W.
Klar, wer in den Fluss schaut , sieht sich selbst.
Mit dem Verständnis der Lichtbrechung konnte man eine Brille erfinden.
Eine der wichtigsten Erfindungen überhaupt.
Es bleibt trotzdem ein Widerspruch. Was wir sehen, sind nicht wir, sondern das Spiegelbild.
Als ich zum ersten Male meine Stimme hörte, auf Tonband, war ich irritiert. bin ich das ?
Welchen Vorteil hat es, dass die linke Gehirnhälfte für
die rechte Körperhälfte zuständig ist, und umgekehrt?
Dass das Bild in den Augen umgekehrt ist,
das ist vermutlich nicht die Ursache?
Leicht gekrümmte Fensterscheiben erzeugen interessante Sonnenbilder:
http://s880616556.online.de/MAITREYA.jpg
Der Zauberspiegel Mirage von Opti-Gone zeigt Dinge, an Orten, wo sie gar nicht sind.
Zwei Parabolspiegel bei denen der Brennpunkt des einen Spiegels im Scheitelpunkt des anderen Spiegels liegt.
Der obere Spiegel hat in der Mitte eine Öffnung.
https://wissenstexte.de/physik/zauber_4.png
Karl Bednarik
lässt sich ein virtuelles Bild spiegeln ?
Hallo Wengert,
ein virtuelles Bild kann man auch mit mehreren flachen Spiegeln umleiten (siehe die Unsichtbarkeit mit dem lila Plüschhasen).
Das virtuelle Bild entsteht nur im Gehirn des Betrachters, weil das Sehzentrum annimmt, dass die Lichtstrahlen geradlinig vom Objekt her kommen (was aber täuscht).
Ein reelles Bild kann man immer mit einem weißen Blatt Papier auffangen und darstellen, und es kann nur mit Hilfe von Hohlspiegeln oder Sammellinsen entstehen (muss aber nicht immer).
Echte Nostalgie (zum Thema passend):
Meine Liege-Programmier-Vorrichtung
von 1984 mit dem Commodore VC 20:
http://s880616556.online.de/USIMOD-5.JPG