Gerade weil die Informatik-Laureaten beim HLF in der klaren Mehrheit sind, war es interessant zu sehen, welche große Rolle die reine Mathematik in den bisherigen HLF-Vorträgen gespielt hat – über die zum Teil sehr tiefreichenden Verbindungen der beiden Fächer.

Der Vortrag von Tony Hoare am Dienstag ist dabei sicherlich am weitesten in die Vergangenheit vorgestoßen. Hoare hat die Vorläufer der Informatik bis zurück zur Logik des Aristoteles verfolgt. Der damalige Schlüsselschritt: Die Trennung zwischen der Form des Beweises und dem Inhalt seiner Aussagen. Wenn alle Griechen Menschen sind und alle Menschen sterblich, dann sind eben auch alle Griechen sterblich – und der Beweis lässt sich in einer allgemeinen Form formulieren, die weder etwas von Griechen noch von Menschen und Sterblichkeit weiß.

Die modernen Abkömmlinge dieser Aufteilung betreffen einen Bereich, in dem die Informatik der Mathematik gehörig unter die Arme greifen kann: die Entwicklung generischer computergestützter Beweise. Das Adjektiv “generisch” ist dabei entscheidend. Gegenüber maßgeschneiderten computergestützten Beweisen haben Mathematiker ein gesundes Misstrauen – solche Beweise nutzen typischerweise umfangreiche Computerprogramme, und deren Richtigkeit nachzuprüfen, Zeile für Zeile, kann sich als schwierig bis praktisch unmöglich herausstellen.

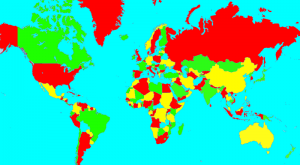
Ein solcher Beweis betrifft das sogenannte Vierfarbentheorem (siehe Abbildung). Es wurde erstmals 1976 von Kenneth Appel und Wolfgang Haken mithilfe eines maßgeschneiderten Computerprogramms bewiesen. Ein jüngerer Fall ist die Kepler’sche Vermutung, bei der es um das optimale Verfahren geht, gleichgroße Kugeln wie z.B. Orangen in eine große Kiste zu packen. Der erste computergestützte Beweis der Vermutung, vorgelegt von Thomas Hales im Jahre 1999, bestand aus 250 Seiten von Notizen plus 3 Gigabyte an Computercode und Daten. Nachdem der Beweis zur Veröffentlichung eingereicht worden war, konnte ein zwölfköpfiges Team von Gutachtern nach vier Jahren Auseinandersetzung mit dem Material nichts weiter sagen, als dass sie zu 99% sicher wären, dass der Beweis stimmen würde. Keine sehr beruhigende Aussage für Mathematiker.

Deswegen ist generische Beweisprüfungs-Software so wichtig – als moderne Form von Aristoteles Trennung von Struktur und Inhalt eines Beweises. Solche Software weiß nichts von Farben, Flächen, Grenzen oder Orangen. Aber sobald ein Beweis in der richtigen Form aufgeschrieben ist, kann die Software prüfen, ob die Beweisschritte logisch aufeinander aufbauen. Und sobald die Software ihrerseits einmal von Mathematikern geprüft und für korrekt befunden ist, kann man sie auf eine Vielzahl verschiedener Beweise anwenden.

Im Jahre 2005 veröffentlichte Georges Gonthier einen Beweis der Vierfarben-Theorems, der die generische Beweisprüfungssoftware Coq nutzte – nebenbei bemerkt: diese Software kam gleich in einer ganzen Reihe von HLF-Vorträgen vor. Ein später Erfolg für Aristoteles und sein Trennungsverfahren! Auch Thomas Hales war mit den 99%, die ihm bescheinigt worden waren, offenbar unzufrieden. Im Januar dieses Jahres veröffentlichte er einen Beweis für die Kepler’sche Vermutung, der ebenfalls generische Beweisprüfungs-Software nutzte.

Unter anderem in dieser Weise ist die reine Mathematik beim diesjährigen HLF gut vertreten – dank tiefer Verbindungen zwischen den beiden Fächern, die sich aus unseren Tagen bis zu Aristoteles zurückverfolgen lassen.

Wie alle HLF-Vorträge ist auch der von Hoare online und kann hier angeschaut werden.