10 out of 200: Between string art and integrable systems – Tamás Görbe brings math to life

Meet Tamás Görbe, mathematician and one of this year’s 10 out of 200 young researchers participating in the 6th Heidelberg Laureate Forum from September 23-28, 2018.

What is your name and nationality?
My name is Tamás Görbe and I’m from Hungary.
Where did you study and where are you currently based?
I did my studies at the University of Szeged, Hungary and I’m currently based at the University of Leeds.
What is your current position?
I’m a Marie Curie Research Fellow in the School of Mathematics, University of Leeds.
What is the focus of your research? What is your research project?
My research area is Integrable Systems, which is a vibrant crossroads of mathematics and physics. In particular, I study integrable models of Calogero-Ruijsenaars type. These models describe interacting particles that move on a line or circle. Although the interaction between these particles leads to a rather complicated (i.e. nonlinear) dynamics, the equations of motion, such as Newton’s F=ma or the Schrödinger equation can be exactly solved. This is nothing short of a miracle! The reason behind this is Integrability, which roughly means the existence of many conserved quantities (like energy or momentum). Here’s a very simple example:

We see three particles that are pushed towards each other. Initially, they have lots of kinetic energy, but as they get close a repulsive force takes over and slows them down. The situation is similar to the repulsion of like charges, but instead of Coulomb’s law we have an inverse-cube law. As the kinetic energy drops, potential energy builds up (that’s why the particles “blush”), so the total energy does not change. Then they scatter and go off to infinity. It turns out that energy is not the only thing that is conserved. In fact, there are two additional conservation laws making as many as there are particles. This can be understood by drawing the space-time diagram of the particles:
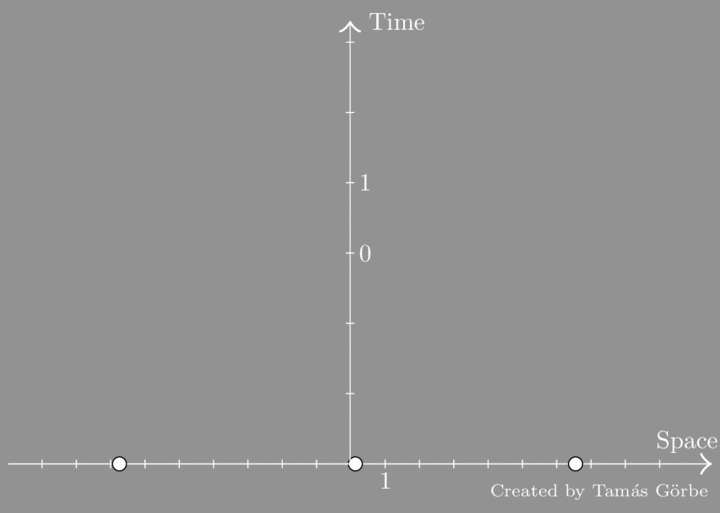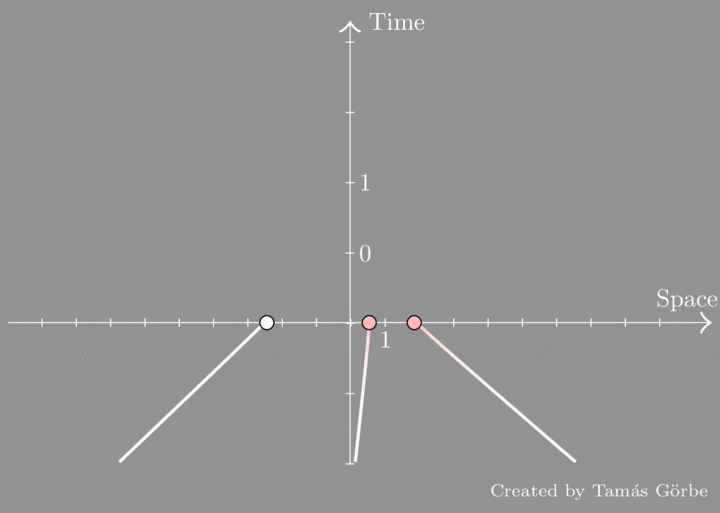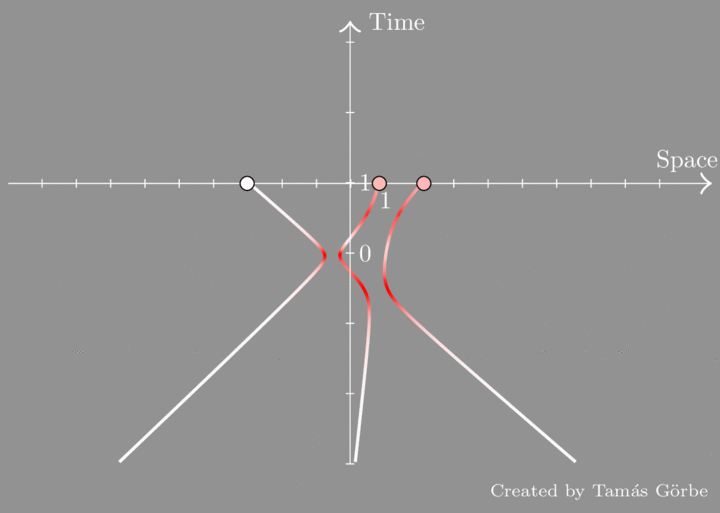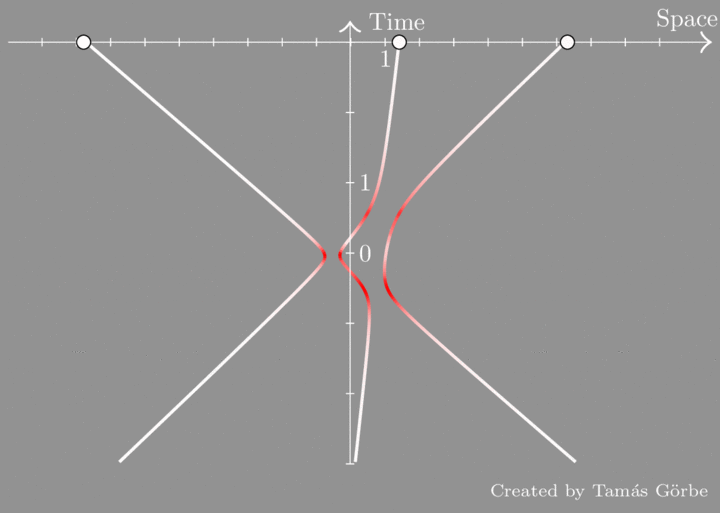
The first thing to notice is the red spots on the trajectories. They occur in pairs, which means that the scattering is factorized into 2-body processes. Another thing to observe is that the trajectories at the “distant past and future” are straight. Moreover, the slopes are interchanged meaning that the particles exchange their initial speeds by their interaction. These 3 slopes are conserved.
By a beautiful result, known as Noether’s theorem, these conservation laws point to hidden symmetries of the models. My job is to find out what these hidden symmetries are. Recently, I started a research project that aims at finding new integrable models, related algebraic structures, and connections to various field theories.
Why did you become a mathematician?
I always liked looking for patterns and connections. Mathematics is all about that. Luckily, I had fantastic teachers who helped me in pursuing this passion of mine.
What are some of the fundamental challenges you have faced in your academic career?
Handling the pressures of academic life. It’s a constant challenge, but I’m getting better at it.
What do you feel are the greatest pressures facing scientists today?
I think scientists need to make sure that people’s trust in Science and its methods is maintained in this world of fake news.
What are you doing besides research?
I spend much of my free time with science communication. This includes various activities. First of all, I enjoy making string arts to help people visualize and appreciate abstract concepts that are relevant to my research. Take root systems, for instance. These are very symmetric configurations of points, which live (mostly) in dimensions higher than 3, so they’re hard to imagine. Using pins and colourful threads, I construct their 2D projections at which people can look and say “Now I see what you mean by beautiful mathematics!”

Another project, which I started this year, is a weekly series on Twitter featuring the most important/beautiful equations and formulas in maths and physics. It’s called #Weeqly. In addition, I give public lectures on topics related to my research, such as Symmetry and Conservation laws. Finally, I have a somewhat abandoned blog about maths and physics, which I’m planning to restart soon.
How did you hear about the HLF and why did you apply?
I first heard about the HLF through Lynn Heller when I was at an LMS Durham Symposium two years ago. She told me about her experience as a participant of the 3rd HLF and encouraged me to apply.
What do you expect from this meeting?
I think attending the forum is a great opportunity to meet and get to know people outside my research field. Such acquaintances carry a real potential of turning into fruitful collaborations.
Which laureates present at the forum would you really like to talk to and what do you want to ask them? There are just so many amazing individuals, it’s hard to make a list. But to name a few people, I always like to listen to Sir Michael Atiyah’s stories. I’d also like to talk to Artur Ávila, Chaucher Bikar and Peter Scholze.
Who were your most important mentors and what lessons did they pass on to you?
My high school math teacher, János Mike. He taught me that humility and persistence can go a long way.
What is an everyday life example for Calogero-Ruijsenaars type models, which you are working on?
They tend to pop up in the most unexpected places. They appear in the study of surface waves of shallow water, the theory of optical fibers, and even lipid membranes.

