Was ist Reibung? Thermodynamische Fußnote
Überträgt man Wärme, wenn man an einem Körper reibt? Eine beliebte Pfrüfungsfrage, an der Studierende regelmäßig scheitern, weil der Wärmebegriff Schwierigkeiten macht.
Gleich zur richtigen Antwort: Entgegen aller praktischen Vorstellungen – von romantischen zu schweigen – übertragen wir nicht Wärme sondern leisten Arbeit an einem Körper, wenn wir ihn reiben. So ist die Definition der Wärme, beziehungsweise der Größe \(Q\), die wir Wärme nennen.
Dabei ist es nicht die eng begrenzte Definition der Größe \(Q\) sondern ihr Benennung als „Wärme“, die ganz natürlich Schwierigkeiten bereitet. Denn sie steht der umgangssprachlich geprägten Intuition entgegen. Das darf man zumindest einmal vermuten. Natürlich müsste man es empirisch nachweisen. Auf die Umgangssprache komme ich ganz am Ende nochmal zurück.
Um das Thema Reibung ein wenig anschaulicher zu erklären, wollte ich wie immer nach frei verfügbaren Bildern im Internet suchen. Nach Eltern, die ihr Kind nach dem Duschen mit einem Handtuch abtrocknen und warm reiben. Ein Sekunde später habe ich es mir anders überlegt.
Nicht \(Q\) sondern \(W\)
Stattdessen fange ich mit dem ersten Hauptsatzes der Thermodynamik an. Der sagt, dass sich die innere Energie \(\Delta E\) des nach der Dusche frierenden Kindes (es wurde natürlich am Ende eiskalt abgeduscht!) nur durch Arbeit \(W\) und durch Wärme \(Q\) ändern lässt. Etwas drittes gibt es nicht, kurz&knapp: \(\Delta E=W+Q\).
Wenn das saubere Kind nun aufgewärmt, im Bademantel isoliert und mit einem Glas Milch in der Hand Sandmänchen schaut, hat die Mutter durch ihr Trockenreiben zuvor Arbeit verrichtet jedoch damit keine Wärme übertragen. So nüchtern müssten Physikerinnen die Situation beschreiben. Vielleicht würden einige gestresste Eltern sogar noch mit fast geschlossenen Lippen langsam ausatmend zustimmen, doch in der Regel haben wir ein völlig anderes alltägliches Verständnis von dem Begriff Wärme.
Dissipation gehört zu Reibung
Die Arbeit der Mutter wird dissipiert. Dissipation gehört unmittelbar zur Reibung. Wärme gehört nicht unmittelbar zur Reibung. Man könnte auf die Idee kommen, die Reibung geht in thermische Energie über, was wiederum – und an dieser Stelle würde es zumindest ungenau, wenn nicht gar falsch, wie weiter unten erklärt – Wärme sei. Um den Anfang des Arguments zu veranschaulichen, der Studierende zuverlässig in die Irre führt, komme ich nochmal auf das Glas Milch zurück. Die Milch in dem Glass ist aus guten Gründen keine Glasmilch.
Wir ersparen uns viele Worte, wenn wir auf nutzlose Differenzierungen verzichten. Es ist zwar oft bequem, kurz von Flaschen- oder Tütenmilch zu sprechen, aber ziemlich unnütz, das Umfüllen oder Trinken deswegen als Milchumwandlung zu formulieren und den Inhalt des Trinkglases oder des Magens als besondere Milchformen zu definieren. Bei der Energie ist es kaum anders. Die sauberste, wenn auch nicht die bequemste Lösung ist der Verzicht auf alle Energieformen. Natürlich dauert es, wie bei einem Patienten, der nach langem Krankenlager zum ersten Mal seine Krücken aufgibt, bis man sich an den neuen Zustand der Freiheit gewohnt und auch schwierige Stolperstrecken unbeschadet zu überwinden gelernt hat. [Georg Job†]
So werden die Energieformen zu Altlasten der Physik erklärt.† Genau in diesem Sinne ist der Begriff „thermische Energie“ an dieser Stelle unnütz, denn er führt zu falschen weiteren Vorstellungen.
Die Situation ändert sich nicht, ja sie wird sogar verständlicher, wenn die Reibung nicht an der Systemgrenze stattfindet. In der Tat darf man in einer Prüfung die Eingangsfrage als ill-defined abtun, da die Arbeit an der Systemgrenze geleistet wird. Das heißt aber bloß, wir können nichts weiter ausrechnen. Die Tatsache, dass Reibung nichts mit Wärme zu tun hat, bleibt davon unberührt und sollte in der Prüfung auch erwähnt werden. Aber Vorsicht!
Verlegen wir zunächst also die Systemgrenze weiter nach außen. Wir schauen nicht auf das Kind, wobei Mutter mit Handtuch dessen Umgebung darstellten. Wir schauen auf das Badezimmer mit Kind und Mutter drin.
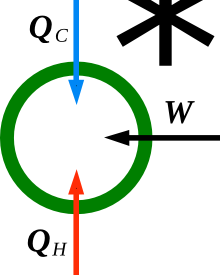
Nur ein wenig abstrahiert ist das vergleichbar mit dem rechts abgebildeten Joule-Apparat. Die Arbeit wird nun vollständig im System also im Badezimmer bzw. Joule-Apparat dissipiert. Jetzt kann man rechnen! (Was ich hier nicht tun will.)
Irreversible Wärme ist keine Wärme sondern alias für dissipierte Arbeit
Warum darf man nicht sagen, die Arbeit wird in Wärme umgewandelt? Man könnte das sogar in der Tat so sagen, aber nur, wenn man einen entscheidenden Zusatz macht.
Die Reibungsarbeit erhöht die innere Energie. Es gibt nun die Möglichkeit, diese dissipierte Arbeit \(W\) als irreversible Übertragung von Wärme (\(Q_{ir}\)) zu umschreiben. Warum man das tun sollte? Dafür gibt es einen und nur einen Grund: Weil man den Zugewinn an Entropie \(S\) über \(S=\int \frac{\delta Q}{T}\) ausrechnen soll – und dafür braucht man ein \(Q\), das über die Systemgrenze übertragen wird aber danach nicht im System enthalten ist!
Die Größe \(Q\) im ersten Hauptsatz ist allein das, was in der Physik im konkreten Sinne als Wärme bezeichnet wird. Diese Größe ist immer die reversible Wärme (\(Q_{rev}\)). Die Größe \(Q_{ir}\) ist eine Stellvertretergröße, sie ist nicht Wärme selbst! Sie ist ein Äquivalent, das man für eine Berechnung mittels \(S=\int \frac{\delta Q}{T}\) heranziehen kann. Die Größe \(Q_{ir}\) ist in diesem Sinn nichts als eine Abkürzung. Denn eigentlich sucht man nach einem thermodynamischen Prozess, der den gleichen Anfangs- und Endzustand hat, wie der Prozess der inneren (d.h. vollständig im System dissipierten) Reibung. Dieser Ersatzprozess erlaubt es, die Entropie \(S\) zu berechnen. Statt über diesen Ersatzprozess nachzudenken (was man fast ebenso leicht tun könnte), geht es noch schneller einfach \(Q_{ir}=W_{dissipiert}\) anzusetzen.
Wer über über Thermodynamik nachdenkt, kommt nicht umhin festzustellen, dass wir im Prinzip das Pferd von hinten aufzäumen. Wir beginnen mit \(Q\) im ersten Hauptsatz und kommen darüber, nämlich über \(\int \frac{\delta Q}{T}\), zu der Entropie \(S\). Das ist bedauerlich.
Richtig (sowohl im Sinne von grundlegender wie auch historisch entstanden) wäre es, mit dem zweiten Hauptsatz und der Entropie \(S\) zu beginnen und über \(\delta Q = T dS\) die Größe \(Q\) zu bestimmen (wenn man sie denn anführen möchte). Die Reihenfolge der Hauptsätze führt an dieser Stelle aber zu weit.
Umgangssprache
Selbst wenn man mit Entropie \(S\) beginnt und damit zu \(Q\) kommt, bleibt die Frage, wie man diese Größe benennt. Deswegen sollte man zum Abschluss nochmal auf die Umgangssprache kommen.
Umgangssprachlich kann und wird man „Arbeit„ und „Wärme„ unterschiedlich nutzen.
„Der Polizist leistet Arbeit.“
„Die Meeresströmung enthält Wärme.“
Dass hingegen etwas „Arbeit enthält“ scheint mir weniger üblich im Sprachgebrauch, abgesehen von der Metapher „da steckt viel Arbeit drin“. Dass „Wärme geleistet wird“ scheint mir noch unüblicher.
Durch diese sprachliche Unterscheidung erscheint es dem Anfänger auch im physikalischen Sinn möglich, dass an einem System Arbeit geleistet wird, z.B. durch Reibung, und es deswegen nun mehr Wärme enthält.
In der Physik stehen allerdings Wärme \(Q\) und Arbeit \(W\) in direkter Konkurrenz zueinander. Sie stehen in einem entweder-oder-Verhältnis, wie etwa „spazieren“ und „rennen“. Wenn eine Wegstrecke zurückgelegt wurde, kann man einen Teil davon rennen, den Rest spazieren. Man kann aber nicht ein Stück gleichzeitig rennen und spazieren.
Hinzu kommt, dass in der Physik „Wärme“ auch als Oberbegriff gebraucht wird. Zumindest in der zusammengesetzten Form „Wärmelehre“, die sicher nicht die allein die Lehre von \(Q\) ist sondern auch (und mehr noch) von Energie, Entropie und der Temperatur. Früher war es üblich „Wärme“ nur als Oberbegriff zu gebrauchen und \(Q\) als „Wärmemenge“ zu bezeichnen (was allerdings für eine Prozessgröße auch ungewöhnlich klingt, da „Menge“ eine Erscheinungsform nahelegt).
Das Phänomen der Reibung zeigt vielleicht am deutlichsten, dass es ein Problem ist, dissipierte Arbeit und Wärme neutral unter dem Oberbegriff Wärme zusammenzufassen. Die Frage, die gestellt werden muss, ist, ob wir „Wärme“ als Oberbegriff strikt vermeiden oder ob wir \(Q\) mit „Wärme“ richtig benennen?
Fußnote zu Fußnote
† Das Zitat stammt von Georg Job aus: F. Herrmann und G. Job: Altlasten der Physik, AULIS Verlag Deubner (2002), und ist hier als pdf hier verlinkt.
Ich habe bisher nur sehr wenige Kapitel dieser „Altlasten“ gelesen. Mit dem damit verbundenen Karlsruher Physikkurs (KPK) habe ich mich gestern erstmals und nur durch die Sekundärliteratur beschäftigt. Prof. Herrmann schreibt auf der verlinkten Seite: „Wer KPK-Gedankengut entdeckt, ist aufgefordert, es der DPG zu melden“. In der Tat gibt es KPK-Gedankengut bei mir im Blog zu entdecken. Denn soweit ich es gelesen habe, ist die Thermodynamik einwandfrei und insbesondere die Verwendung von „Wärme“ als Oberbegriff auch für Entropie finde ich sehr spannend. Also nur zu.
Dank eines Leserkommentar zum letzten Beitrag bin ich auf diese Diskussion zum KPK aufmerksam geworden. Wesentliche Teile dieses sowie älterer wie noch folgender Beiträge habe ich im Juli in Toronto geschrieben. Sie decken sich auffällig mit der Sicht insbesondere von Georg Job und anderen Thermodynamikern, die sich über die Grundlagen Gedanken gemacht haben.
Bildquelle
Joule Apparatus CC BY-SA 3.0, Dr. Mirko Junge


Die Redeweise von der “Wärmemenge” mag ein Relikt aus Zeiten der kalorischen Theorie der Wärme sein, dort würde es besser hinpassen. Die mit einer Theorie verbundenen Vorstellungen können schliesslich auch dann noch fortbestehen, wenn die Theorie obsolet geworden ist, zumal wenn diese Vorstellungen vergleichsweise einfach zu begreifende Bilder vermitteln.
Eine Vermischung von Konzepten ganz unterschiedlicher theoret. Herkunft kann sich jedoch auch zum Verständnisproblem auswachsen. Die typische Physik-Didaktik ist zumindest im Grundstudium nach meiner Erfahrung auch nicht auf die Vermittlung von konzeptuellem Verständnis ausgelegt, sondern auf das Einüben bestimmter Praktiken, deren Beherrschung dann in Examina geprüft wird, und deren Sinn oder Unsinn sich einem vielleicht irgendwann später einmal erschliesst, wenn man Glück hat. Die “thermodynamischen Fussnoten” hier scheinen mir daher eine hervorragende Idee, um gerade dort Klarheit zu schaffen, wo ansonsten viele Nebelschwaden herumwabern.
Stimmt, zurück gehen zur “Wärmemenge” wäre keine gute Lösung.
Erwähnenswert halte ich es, weil damit der Begriff Wärme als (loser) Oberbegriff frei war. Man konnte damals sagen, Temperatur ist ein Maß (ein Grad) für Wärme, Entropie ein anders Maß. Analog zur Arbeit ist Q der Übergang von Energie die die Wärme ändert usw. Da Wärme heute für Q steht, muss man bei diesen Formulierungen vorsichtig sein.
Zur Didaktik der Physik: siehe hier.
Durch die Fussnoten inspiriert, hatte ich mich noch etwas auf die Suche gemacht und war auf zwei Fundstücke gestossen, die mir in diesem Zusammenhang interessant erschienen. Bereits nach kurzer Begutachtung finde ich da einiges, was mir noch unbekannt war. Zum einen,
Mendoza, E. (1961). A sketch for a history of early thermodynamics. Physics Today, 14(2), 32-42. DOI: 10.1063/1.3057388
Demnach wurde insbesondere der Begriff Wärmemenge (“quantity of heat”) offenbar von Joseph Black eingeführt. Zum anderen,
Uffink, J. (2001). Bluff your way in the second law of thermodynamics. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 32(3), 305-394. [Download]
Uffink bringt da u.a. ein markantes Zitat von Vladimir Arnold (das mir ausnahmsweise nicht ganz neu war):
Und so ist es. Das sagt dann wohl auch etwas aus zum Stand der Physik-Didaktik.
Danke für die Hinweise. Ich hatte von Joseph Black gelesen (glaube in “Mere Thermodynamics”).
Dafür war mir Vladimir Arnold neu. Bin nicht mal sicher, ob ich es richtig verstehe …
Es ist schon bemerkenswert, wie unterschiedlich die Einschätzungen der Thermodynamik ausfallen. Während die einen davon regelrecht entzückt sind, beklagen andere die formale Dürftigkeit ihrer Ausdrucksmittel. Mehr oder weniger erfolgreiche Bestrebungen nach einer rigorosen Geometrisierung der Thermodynamik wurden verschiedentlich unternommen, offenbar beginnend mit Gibbs, und das war wohl auch das Thema von Arnold (dessen Text mir jetzt nicht zur Hand ist). Insgesamt fehlt mir da der Überblick. Immerhin ist Uffinks Referenz (Jauch 1975) ein für meine Begriffe gut und solide geschriebener Text, wo sich im Appendix auch einige allgemeinere Bemerkungen zu dieser Problematik finden lassen. (N.B. Jauchs Paper ist mit “Part I” betitelt. Zum angekündigten Part II scheint es nicht mehr gekommen zu sein, da J.-M. Jauch im August 1974 verstorben ist.)
Jedenfalls scheinen mir die Begriffsbildungen zur Thermodynamik in typischen Lehrtexten so beschaffen, dass durchaus ein nennenswerter Bedarf an weiteren klärenden Fussnoten gegeben ist.
Energieformen
Meinem alten Biophysik-Lehrbuch (1988) entnehme ich, dass physikalisch-chemische Vorgänge an unbelebten und belebten Systemen im Allgemeinen mit „Energieumwandlungen“ verknüpft sind. Eine der wichtigen Aufgaben der Thermodynamik sei es daher, zunächst die verschiedenen, über die Systemgrenzen transportierten „Energieformen“ quantitativ zu erfassen, worauf dann in der Regel eine „Energiebilanz“ gezogen werden kann, und am Ende kann man dann zu Aussagen über die Natur der ablaufenden „Prozesse“ kommen.
Mir fällt es schwer, zu verstehen, warum es irreführend, wenn nicht gar falsch sein soll, zu sagen, dass Wärme (und Arbeit) im Grunde Energieformen sind oder zumindest als solche zu betrachten sind. Das geht doch auch unmittelbar aus der Gleichung
ΔE=ΔQ+ΔW
hervor.
Wären ΔQ und ΔW (oder Q und W) keine Formen der Energie, sondern bloß „Prozesse“, wie könnte denn dann die (innere) Energie eines Systems zu- oder abnehmen?
Es sind Übergangsformen. Da steckt ja immer noch das Wort From drin. Man darf also (wenn man denn unbedingt will) auch als Energieform sehen, solange man die Einschränkung auf den Prozess mitdenkt. Ist die Wärme oder Arbeit erstmal im System als innere Energie enthalten, gibt es keine sinnvolle Aussage der Art, 23% davon sind Arbeit und 77% durch Wärme. Jetzt ist es nicht mal sinnvoll an 100% innere Energie zu denken, denn die innere Energie hat ja eine beliebige Nullpunkverschiebung. Daher bekommt E ein Delta und W und Q keins.
@Balanus
Da hilft vielleicht Mikhail Volkenstein noch weiter, der schliesslich auch Biophysiker war und die Angelegenheit ziemlich detailliert abhandelt. Er verwendet zwar eine andere Vorzeichenkonvention und nimmt \(W\) als die vom System geleistete Arbeit, das stört aber hoffentlich nicht. In meiner Ausgabe ist es die Formel (1.7), die dann lautet
\(\Delta E = E_1 – E_0 = Q – W\),
und auf die er später bei den Hauptsätzen wieder zurückkommt.
Zu beachten wäre, dass \(E\) eine Funktion auf dem Zustands- oder Phasenraum eines thermodyn. Systems ist, was aber für \(Q\) und \(W\) nicht gilt. Die andere Formel mit den Deltas erweist sich spätestens dann als formal problematisch, wenn man von Differenzen zu Differentialen übergehen will, denn nur \(dE\) ist dann tatsächlich ein Differential, wohingegen die anderen Grössen eine andere Darstellung erfordern.
Ein der Sache angemesseneres Aufzäumen des thermodynamischen Pferdes könnte also im Prinzip vom ersten Hauptsatz in der Form
\(dE = \theta + \mu\)
ausgehen, wobei die Pfaffschen Formen \(\theta\) resp. \(\mu\) als so etwas wie ein thermischer resp. mechanischer “Zustrom an Energie” zu betrachten wären. Die Grössen \(Q\) und \(W\) lassen sich dann erhalten durch Integration dieser Formen längs des Weges \(C\), den das in Betracht stehende System während des Prozesses des “Energiezustroms” im Phasenraum absolviert, d.h.
\[Q = \int_C \theta \quad \mbox{und} \quad W = \int_C \mu.\]
Entsprechend natürlich auch für die innere Energie, aber da \(dE\) exakt ist, beschreibt das Integral dann nur die Energiedifferenz zwischen Anfangs- und Endpunkt des Weges, was hier ein Delta rechtferigt.
Didaktisch liegt darin freilich eine gewisse Herausforderung, wie man die dabei auftretenden Grössen motiviert, wie man sie sinnvoll benennt, und welche Vorausetzungen es braucht, um die Angelegenheit überhaupt begreifbar vermitteln zu können.
Ob das wirklich hilft? Ich denke, man sollte nicht mit dem 1HS anfangen, sondern mit Konzept der adiabatischen Erreichbarkeit. Dort kommen die Pfaffschen Formen ja auch vor.
Allerdings muss ich zugeben, würde ich heute einen Kurs lehren, ich würde ihn wohl klassisch aufziehen, denn das wäre die geringste Arbeit. Ich will also gerne unterscheiden zwischen einen wirklich neuen Entwurf und den etwas pragmatischeren herangehen. Bei letzterem würde vielleicht schon eine etwas sorgfältigere Notation und Benennung sehr helfen.
Die Formulierung: dE = “thermischer oder mechanischer Zustrom an Energie” scheint mir didaktisch gelungen. Die Einführung von Q und W als Integrale über einen Weg im Phasenraum ist aber bereits ziemlich involviert und müsste mit aus didaktischer Sicht gut ausgewählten Beispielen erklärt werden. Oder beinhaltet der Weg C im Phasenraum gar kein bestimmtes Vorgehen sondern ist nur ein Name für alles Denkbare was Arbeit oder Wärme zuströmen lässt?
Okay, doch auch wenn man bevorzugt vom zweiten Hauptsatz ausgeht, stellt sich (nicht zuletzt didaktisch) die Aufgabe, dem ominösen Symbol \(\delta Q\) eine fassliche Bedeutung zu geben. Der traditionelle Zugang, dabei mit einem obskur belassenen \(Q\) zu beginnen, kann schwerlich der Weisheit letzter Schluss sein, denn das ist weder formal befriedigend noch dem Verständnis sonderlich hilfreich, wie sich bei der “Delta-Frage” zeigt. Beim richtigen Aufzäumen wäre jedenfalls zu beachten, dass man eigentlich vom \(\delta Q\) zum \(Q\) gelangt und nicht etwa umgekehrt.
Das KPK-Bild von einem Strom scheint mir hierfür grundsätzlich nicht so daneben (ohne jetzt Details der dort gegebenen Darstellung zu kennen). Ob und gegebenenfalls wie man das dann für Anfänger möglichst begreifbar gestalten und anhand erläuternder Beispiele motivieren kann, ohne zuviel an Formalismus herankarren zu müssen, erfordert sicherlich einiges an didaktischem Engagement.
Wie schon angedeutet, meine eigenen Erfahrungen aus der Studienzeit mit dem Thema waren eben so, dass ich irgendwann später das obige Zitat von V.I. Arnold noch als sehr beruhigend und bestätigend empfand.
Arnold Sommerfeld soll übrigens über die Thermodynamik gesagt haben:
“Thermodynamik ist ein komisches Fach. Das erste Mal, wenn man sich damit befasst, versteht man nichts davon. Beim zweiten Durcharbeiten denkt man, man hätte nun alles verstanden, mit Ausnahme von ein oder zwei kleinen Details. Das dritte Mal, wenn man den Stoff durcharbeitet, bemerkt man, dass man fast gar nichts davon versteht, aber man hat sich inzwischen so daran gewöhnt, dass es einen nicht mehr stört.”
(Fand ich in: Was ist Entropie? Eine Antwort für Unzufriedene)
Zum Thema: muss man denn \(Q\) überhaupt einführen? Man hat doch auch fast nie ein \(W\). Und wenn, dann nennt man es thermische Arbeit und schreibt \(W_{th}\) oder sowas.
Das ist nur eine Idee, bin mir selbst unsicher, ob sich das durchhalten lässt.
Das Zitat von Sommerfeld zur Thermodynamik gefällt mir auch ausgezeichnet, das kannte ich noch nicht.
Wenn man die Entropie bereits hat, dann braucht man das \(Q\) natürlich nicht extra einzuführen. Man bekommt es gratis, wenn man es unbedingt haben will, aber es ist nicht so unbedingt essentiell.
Andererseits scheint das \(Q\) auch nicht auf, wenn man nur irgendwie an die 1-Form \(\theta\) kommt. Und sofern die erste de Rham Gruppe des Phasenraums trivial ist, lässt sich der zweite Hauptsatz auch formulieren als
\[d(T^{-1} \theta) = 0\].
Die Voraussetzung entspricht der von Theorem S im Paper von Borchers (das ich jetzt auch in meiner Sammlung habe, vielen Dank für den Hinweis darauf). Aus der Geschlossenheit dieser 1-Form folgt in diesem Fall ihre Exaktheit, und so kommt man unmittelbar wieder zur Entropie und \(\theta = T dS\).
Wenn man also entweder \(S\) oder \(\theta\) hat und von allfälligen topologischen Pathologien absieht, dann ist es letztlich gehupft wie gesprungen. Die Frage wäre aber, welches von beiden sich im Rahmen einer Einführung vielleicht besser motivieren liesse, um darauf aufzubauen.
P.S. Danke im übrigen noch für den reparierten missing Backslash!
Ich schaue mir gerade das hier an: “The mathematical structure of thermodynamics“.
(Zuerst ein bisschen gewöhnungsbedürftig, da die gleich \(W\) und \(Q\) als Differntialform definieren und nicht erst auf ein \(\mu\) und \(\Theta\) zurückgreifen, hat dann aber Charme, weil es so klar auf das, was sonst \(W\) und \(Q\) ist, ohne Worte verzichtet)
Ich finde das wegen der klaren Zurschaustellung der Struktur ganz gut (bin gerade erst bei den Maxwell-Beziehung).
PS: “Rham Gruppe des Phasenraums” sagt mir jetzt nichts …
PPS: Backslash ist gern geschehen.
Ja, was bei Salamon et al. als heat form bezeichnet und wieder durch \(Q\) symbolisiert wird, hatte ich \(\theta\) genannt. Und die von mir zuletzt angeführte Formulierung des zweiten Hauptsatzes ist offenbar die von Carathéodory, denn sie bedeutet, dass \(1/T\) ein integrierender Faktor für \(\theta\) ist.
Die genannte Voraussetzung besagt im übrigen nur, dass der thermodyn. Phasenraum einfach zusammenhängend sein soll. Die Forderung, dass jeder geschlossene Weg zusammenziehbar ist, verhält sich dual zu der, dass jede geschlossene 1-Form exakt ist. Letzteres wird durch die de Rham Cohomologie damit beschrieben, dass die erste de Rham Gruppe (eigentlich ein reeller Vektorraum) trivial ist (die Dimension null hat).
Borchers demonstriert das “zu Fuss” bei seinem Theorem S und merkt dazu im letzten Abschnitt an, dass die Bedingung entsprechend auch bei Carathéodory gefordert ist.
Didaktisch wird man wohl kaum die Vorstellung aufgeben können, dass Wärme und Arbeit Energieformen sind, oder Erscheinungsformen der Energie bei ihrer Übertragung von einem Körper auf einen anderen.
Was könnte denn der „thermische Zustrom an Energie“ anderes bedeuten als ein Zustrom an Wärme?
Auch M. W- oder Volkenstein verwendet solche anschaulichen Begriffe, wenn er zur Thermodynamik schreibt, dass es (u. a.) um Prozesse geht, „bei denen Energie von einem Körper auf den anderen übertragen oder eine Energieform in eine andere umgewandelt wird“.
Chrys schreibt: »…nur dE ist dann tatsächlich ein Differential, wohingegen die anderen Grössen (Q und W) eine andere Darstellung erfordern.«
Dann wäre also das, was Adam, Läuger und Stark in ihrem Biophysik-Lehrbuch schreiben, zumindest formal nicht korrekt. Dort heißt es nämlich (für physikalisch-chemische Anwendungen):
Spielt hier die Einschränkung auf physikalisch-chemische Anwendungen eine Rolle, dass es eben um dU geht und nicht um dE?
Die Bezeichnung \(E\) und \(U\) stehen beide für die innere Energie und es gibt keine (sinnvolle) Unterscheidung.
Statt
\( \textrm{d} E = \textrm{d} W + \textrm{d} Q \)
könnte man aber auch so schreiben:
\( \textrm{d} E = \delta W + \delta Q \)
oder
\( \textrm{d} E = \textrm{d}\mkern-5.5mu\raise.6ex\hbox{-} W + \textrm{d}\mkern-5.5mu\raise.6ex\hbox{-} Q \)
schreiben. Damit soll nur gesagt werden, dass man die Differentialformen \( \textrm{d}W\) und \( \textrm{d}Q\) nicht zu je einer Funktion \(W\) und \(Q\) integrieren kann.
Verstehe, bei Adam, Läuger und Stark (1988) wird an anderer Stelle erwähnt, dass dQ (im allgemeinen) kein vollständiges Differential ist. Na immerhin…
Wolkenstein schreibt da präziser:
dE = d‘Q + d‘A
Danke für die Erläuterungen!
@MAD
»Die Bezeichnung E und U stehen beide für die innere Energie und es gibt keine (sinnvolle) Unterscheidung.«
Das ist auch so eine Sache, die es dem Lernenden nicht gerade einfacher macht: Der Laie denkt ja erstmal, in der Physik, und gerade dort, hätte jede Bezeichnung und jedes Zeichen seine besondere Bedeutung.
(das schreibe ich auch deshalb, um „Latex“ oder „MathJax“ zu testen 🙂 )
@Markus A. Dahlem
Eine erweiterte Fassung des obigen Zitates von V.I. Arnold liefert übrigens noch eine Begründung:
Dessen ungeachtet scheint dieser kontaktgeometr. Rahmen für die Thermodynamik erst durch Robert Hermann (1973) explizit formuliert worden zu sein, vgl. dazu auch P. Salamon et al., The mathematical structure of thermodynamics. Was bei Salamon et al. indes nicht genannt wird, ist ein Hinweis auf folgende rigorose Durchführung der Axiomatisierung nach Carathéodory:
Boyling, J. B. (1972). An axiomatic approach to classical thermodynamics. Proc. R. Soc. Lond. A, 329(1576), 35-70.
DOI: 10.1098/rspa.1972.0100
Auf Boyling kam ich letztlich durch T. Frankel, The Geometry of Physics, CUP, 2nd ed. 2006. Ch. 6.3 Heuristic Thermodynamics via Caratheodory.
Während mir inzwischen der geometr. Formalismus zur Thermodynamik (mehr oder weniger konturenhaft) erkennbar wird, bleibt mir doch weitgehend unklar, ob das alles vielleicht aus physikal. Sicht noch für unbefriedigend gehalten wird. Der Ansatz von Lieb und Yngvason beispielsweise ist ja recht aufwendig und wohl eher physikalisch motiviert. Aber irgendwie habe ich bis jetzt verpasst, was eigentlich das Problem ist, das Lieb und Yngvason da umtreibt.
In obiger Diskussion sind ein paar Unklarheiten. Nicht im Phasenraum (der analytischen Mechanik) wird weg-integriert, sondern auf der Zustandsfläche.
Die Thermodynamik müsste eigentlich “Thermostatik” heißen. Eine echte umfassende Nicht-Gleichgewichts-Thermodynamik existiert nach wie vor nicht. In diesen Themenkreis fallen auch die Anstrengungen von Lieb und Yngvason – wobei es da noch tiefer geht, denn es reicht nicht, nur auf einem “Niveau der Theoretischen Physik” zu arbeiten, sondern es braucht rigoros die “Mathematische Physik” inklusive vollständiger Beweise und einer Axiomatik.
Eine rigorose Thermodynamik kämpft schon im Ansatz damit, erklären zu müssen, wie sich makroskopische Observablen von mikroskopischen Observablen unterscheiden. Auf dieses Problem stieß bereits JvNeumann in den 1930ern, es ist in seinem Buch über Quantenmechanik angerissen, aber nicht gelösen.
Die rigorosen Formulierungen einer Thermostatik aus der statistischen Physik und des thd. Limes mit Hilfe von C*-Algebren ab etwa 1960 bringen zwar Licht in die Angelegenheit von Gleichgewichtszuständen, sind aber meines Wissens für das Nicht-Gleichgewicht nicht völlig ausgeführt.
In diesem Sinn ist die klassische Thermodynamik bei Prozessgrößen insofern unvollständig, als diese Prozesse in der Thd durch Wege auf einer Fläche von Gleichgewichtszuständen beschrieben werden; daher gibt es dann auch Hilfskonstrukte wie unendlich langsame quasistationäre Prozesse und Ähnliches.
Der Unterschied zwischen Prozessgröße und Zustandsgröße lässt sich durch Wegabhängigkeit/Wegunabhängigkeit motivieren. Dafür sollte man in einem ersten Thd-Kurs zur Veranschaulichung zuerst ein Bild einer typischen Zustandsfläche in einem 3D-pVT-Diagramm bringen, Observablen und Wege erläutern. Die Unterschiede sind dann ähnlich zum Konzept einer nichtkonservativen/konservativen Kraft und der Existenz eines Potenzials.
Weiter oben enstand kurz eine deRham-Verwirrung: Gemeint war offenbar die deRham-Kohomologie.
Die Terminologie ist insgesamt leider eher uneinheitlich und intransparent, gemeint ist im thermodyn. Kontext aber nicht der mechanische Phasenraum.
Sei der Raum der Gleichgewichtszustände als \(\mathbb{R} \times M\) mit lokalen Koordinaten \(E,q^1,\ldots,q^n\) gegeben, dann definieren zumindest einige Autoren den thermodynamischen Phasenraum als das Bündel der 1-Jets reellwertiger Funktionen auf \(M\), was sich mit \(\mathbb{R} \times T^*M\) identifizieren lässt. Mit \(p_i = \partial_i E\) wird die “heat form” \(\theta\) dort dargestellt durch
\[\theta = dE – p_i\,dq^i\]
und lässt sich auch über Wege im thermodyn. Phasenraum integrieren.
Bei genauerer Betrachtung und Besinnung, in meiner Anmerkung steckt noch ein Missverständnis meinerseits, das zu beheben bliebe.
Ich hatte Zustandsvariablen in Anlehnung etwa an Borchers (1985) genommen; dabei ist die Entropie nicht berücksichtigt. Bei dem beschriebenen Vorgehen fehlt mir die dann aber als Variable für die innere Energie E. Konsequenterweise nehmen die Autoren, die ich im Sinne hatte, bei ihrer Konstruktion von Phasenraum die Entropie als extensive thermodynamische Variable sogleich mit hinzu.
Die in diesem Fall erhaltene 1-Form \(dE – y_i dx^i\) repräsentiert nun gerade die Kontaktstruktur auf dem thermodyn. Phasenraum. Zu integrieren ist bei diesem Zugang dann aber grundsätzlich nichts mehr — und das entspricht wohl auch der im Sinne des Blogautors richtigen Aufzäumung des Pferdes.
Eine späte Antwort zu dieser alten Diskussion.
p,q sind mikroskopische Größen. Der Phasenraum der Mechanik bezieht sich nur auf das Mikroskopische.
Die thermodynamischen Größen sind aber makroskopisch und benützen den thermodynamischen Limes; x,y sind nicht mit den p,q gleichzusetzen.
Mikroskopisch kann man zwar über Energiedissipation und auch über Reibung sprechen, das ist aber immer noch etwas anderes als die makroskopische thermodynamische Prozessgröße “Wärme”.
@Markus A. Dahlem
In seinen Vorlesungen über die Entwicklung der Mathematik im 19. Jahrhundert hat Felix Klein einen Exkurs über Thermodynamik, wo er sich u.a. auch kritisch zu deren gängiger Vermittlung äussert. Nicht zuletzt hinsichtlich der Unterscheidung zwischen exakten und inexakten Differentalen schreibt er da:
Daran noch anknüpfend, wäre für den Neuling nicht einiges womöglich leichter begreiflich, wenn mit der Temperatur \(T\) statt der nicht sonderlich intuitiven Entropie \(S\) begonnen würde? Konsequenterweise gelangt man damit zunächst zur Helmholtz Energie \(A(T,q^1,\ldots,q^m)\), deren Beziehung zur inneren Energie \(E(S,q^1,\ldots,q^m)\) durch Legendre Transformation gegeben ist, präziser gesagt, durch \(E = \sup_T(ST + A)\). Die Entropie \(S = -\partial_T A\) lässt sich demnach schlicht als die zur Temperatur \(T\) konjugierte extensive Variable verstehen. Zudem haben wir damit das totale Differential \(dA = -SdT + p_i dq^i\).
Ausgehend von \(E = TS + A\) erhält man nun wiederum \(dE = TdS + p_i dq^i\) (1. Hauptsatz) sowie den integrierenden Faktor \(1/T\) für die heat form (2. Hauptsatz). Für einen adiabatischen Prozess gilt insbesondere \(TdS = 0\), und folglich
\[dE = p_i dq^i = dA + SdT.\]
In diesem Fall stellt der Ausdruck \(SdT\) offenbar gerade die Dissipation von Arbeit dar, also den Beitrag von Reibung, “irreversible Wärme”, wie auch immer. Das erschliesst sich naturgemäss nicht, wenn man immer nur \(\delta Q\) anstarrt.
Ich hoffe, meinen Gedankengang halbwegs nachvollziehbar skizziert zu haben. Jedenfalls habe ich das Gefühl, etwas verstanden zu haben, was mir zuvor verborgen war, und bei dieser Gelegenheit nochmals vielen Dank für die nachhaltig wirkenden Fussnoten.
Danke, das ist interessant. Gucke ich mir noch genauer an!
Da die vorherrschenden Temperaturwerte derzeit zum Nachdenken über Thermodynamik motivieren, hätte ich da noch etwas anzumerken.
Wie J. Uffink (2001) betont, hat Max Planck in seiner Darstellung zwischen umkehrbaren und reversiblen thermodyn. Prozessen unterschieden. Dabei nennt Planck einen Prozess umkehrbar, wenn dieser in seiner zeitlichen Abfolge invertierbar ist, und reversibel, wenn es möglich ist, vom Endzustand nur irgendwie auf eine zulässige Weise wieder zurück zum Anfangszustand zu gelangen. Später habe er dann beklagt, dass dies weitgehend nicht verstanden worden sei und begriffliche Verwirrungen zur Folge hatte.
Ich bin der Meinung, dass Plancks Begriffsbildungen im Rahmen der Kontaktgeometrie vergleichsweise einfach zu formalisieren sind, wenngleich ich das in der Literatur bis anhin nicht konkret gefunden habe. Es liegt nahe, die physikal. zulässigen Prozesse als diejenigen orientierten Wege im thermodyn. Phasenraum \((P,\Theta)\) aufzufassen, deren Orientierung kompatibel ist mit der durch die Kontaktform \(\Theta = dE – TdS – p_i dq^i\) induzierten Orientierung von \(P\). Kurz gesagt, ein stückweise glatter, orientierter Weg \(u:[a,b] \to P\) heisse zulässig, wenn \(\Theta(\dot{u}(t)) \ge 0\) für alle bis auf endlich viele \(t \in [a,b]\) gilt.
Falls dabei strikt die Gleichheit gilt, kennzeichnet dies den Weg \(u\) als umkehrbar, denn mit diesem ist dann auch sein Umkehrweg \(v(t) := u(a+b-t)\) zulässig. Der Weg \(u\) verläuft dann komplett in einer Legendre Untermannigfaltigket von \(P\), und solche repräsentieren im Phasenraum gerade die Gesamtheit der Gleichgew.zustände des in Betracht stehenden Systems.
Allgemeiner ist ein zulässiger Weg \(u\) in \(P\) reversibel, wenn er sich zu einem Zyklus fortsetzen lässt, d.h., wenn ein zulässiger Weg \(v:[a’,b’] \to P\) mit \(v(a’) = u(b)\) und \(v(b’) = u(a)\) existiert. In Plancks Terminologie wäre insbesondere jeder zyklische Prozess reversibel, aber eben nicht notwendigerweise umkehrbar.
In jedem Falle ist für einen zulässigen Weg \(u\) das Wirkungsintegral \(\int_a^s \Theta(\dot{u}(t)) dt\) eine monoton nicht-fallende Funktion von \(s\), die nach meinem Verständnis die im Verlaufe des Prozesses zwischen \(a\) und \(s\) insgesamt dissipierte Energie misst.
Man kennt den Begriff der thermodyn. Länge eines Weges, der auch in Relation zur Dissipation durch den dargestellten Prozess steht, wie e.g. R. Mrugala (2000) beiläufig erwähnt. Ob und gegebenenfalls wie das zu meinen Überlegungen passt, sofern diese korrekt sind, kann ich im Moment nicht sagen. Mir ging es vorrangig schlicht um eine formale Klärung der von Planck verwendeten Konzepte.
Ich finde es ja eigentlich ein wenig zu warm. Doch ein article der mit “Bluff your way …” anfängt macht neugierig. Leider habe ich allerdings keinen Zugang zu Mrugala (2000). Würde mich über ein pdf freuen dahlem (at) physik.hu-berlin.de
Klingt alles spannend.
Übermässige Wärme gestattet immerhin eine prima Ausrede für die Fehler, die man im Schweisse seines Angesichts so produziert.
Meine Verwechselung von HU und TU bei der e-mail hat die beteiligten Mail Transport Agents offenbar nicht überfordert. Schön, wenn wenigstens die IT fehlertolerant funktioniert.
Zum anderen kommen mir mit nunmehr abgekühltem Kopf meine obigen Überlegungen nicht mehr koscher vor. Ein Weg \(u\) im Phasenraum, der einen thermodyn. Prozess darstellen soll, muss auf alle Fälle die Bedingung \(\Theta(\dot{u}(t) = 0\) erfüllen, sonst ist die Energieerhaltung (1. Hauptsatz) längs des Weges verletzt. Wenn überhaupt die Orientierung des Raumes auf diese Weise in Verbindung zu Dissipation und zum thermodyn. Zeitpfeil gesetzt werden kann, dann, so scheint es mir jetzt, ist zumindest noch die mit der Helmholtz Energie assoziierte 1-Form \(dA + SdT – p_i dq^i\) einzubeziehen. Insgesamt ist mir aber noch einiges unklar.
Erfreulich fand ich hingegen, dass Max Plancks Vorlesungen über Thermodynamik (7. Aufl., 1922) bei gutenberg.org erhältlich sind.