Wie liest man Two Line Elements?
BLOG: Go for Launch

Aus gegebenem Anlass. Wie liest man Bahnelemente aus den etwas kryptischen “Two Line Elements”? Ich bin in letzter Zeit so oft gefragt worden, dass ich das jetzt einfach mal hinschreibe. Es lesen zwar erfahrungsgemäß im Schnitt nur etwa 12 Leute meine Artikel – wenn unter diesen 12 Leute aber nun vielleicht acht sind, die mich sonst angerufen oder angemailt hätten und das nun nicht mehr tun, habe ich gerade enorm Zeit gespart.
Was sind Two Line Elements?
Two Line Elements sind ein definiertes Datenformat, mit denen man die Bahn von Satelliten angenähert beschreiben kann (Näheres z.B. auf Wikipedia oder dieser NASA-Seite. Man benutzt dies Datenformat insbesondere für solche Satelliten, die in niedrigen, fast kreisförmigen Bahnen um die Erde fliegen. So niedrigen Bahnen, dass die mittlere Bahnhöhe selbst in Zeiträumen von wenigen Tagen aufgrund der atmosphärischen Abbremsung deutlich abnimmt.
Wirklich genau sind die Angaben zur Bahn prinzipiell nicht, die man den Two Line Elements entnehmen kann. Beispielsweise ändert sich auf einer niedrigen Erdnahn nicht nur die mittlere Bahnhöhe schon über ein paar Tage hinweg deutlich. Auch die Knotenlinie driftet aufgrund der Erdabplattung schon in solch kurzen Zeiträumen, und zwar beträchtlich.
Two Line Elements sind aber dennoch von Nutzen, zumindest dann, wenn man sich ihrer Schwächen bewusst bleibt und sie nur benutzt, um kurzzeitige Vorhersagen zu machen, und solche, für die man keine hohe Genauigkeit braucht. TLEs sind nicht geeignet, um beispielsweise die Kollisionswahrscheinlichkeit exakt vorherzusagen. Aber sie sind durchaus ausreichend, um beispielsweise die Sichtbarkeitsbedingungen bei einem baldigen Überflug über einer Beobachterposition auf der Erde hinreichend genau vorherzusagen.
Wie liest man die mittlere Bahnhöhe aus den Two Line Elements?
Gerade die mittlere Bahnhöhe ist der Wert, der die meisten Leute interessiert, die zwar ansonsten nicht so viel mit Satellitenbahnen zu tun haben, nun aber versuchen, anhand allgemein zugänglicher Two Line Elements zu verstehen, wann und wo ein Raumfahrzeug in die Atmosphäre eintreten wird. Die Zahl solcher Interessenten steigt immer dann sprunghaft an, wenn die Presse darüber berichtet, dass ein besonders großes Objekt vor dem Ende seiner orbitalen Lebensdauer steht.
Man könnte ja nun erwarten, dass gerade so eine wichtige Kenngröße wie die Bahnhöhe an prominenter Stelle zu finden sein muss. Genau das ist aber nicht der Fall. Bahnneigung, Rektaszension des aufsteigenden Knotens, Argument des Perigäums, mittlere Anomalie – all das findet man sofort – aber wo steht, wie hoch das Ding noch ist?
In den Two Line Elements stehen drei Terme, deren Bedeutung sich nicht unmittelbar erschließt. Genau diese drei Terme braucht man aber, und zwar:
- “Mean Motion” mit der Einheit “Umläufe/Tag” und 11 Zeichen, davon zwei Vorkomma- und acht Nachkommastellen und der Dezimalpunkt
- “First derivative of mean motion” mit der Einheit “Umläufe pro Tag2
- “Second derivative of mean motion” mit der Einheit “Umläufe pro Tag3“
Nur, wenn der Abstieg schon ganz steil ist, müssen Sie die Änderung der “Mean Motion” in Betracht ziehen. Die aktuelle Umlaufrate berechnet sich dann als Polynom zweiter Ordnung MM=MM1+(1/2)*MM2*t+(1/6)*MM3*t2. MM1 ist dabei die “Mean Motion” aus den Two Line Elements, (1/2)*MM2 ist der Term “first derivative …”, denn dort wurde der Faktor 1/2 bereits eingerechnet, und (1/6)*MM3 ist genau der Term “second derivative …”, der auch bereits den Faktor 1/6 enthält.
Wie gesagt, der Wert der “Mean Motion” allein reicht für den Hausgebrauch in aller Regel, es sei denn, es geht wirklich schon ganz steil in den Keller. Wie kommt man jetzt von der aktuellen Anzahl der Umläufe, also der Anzahl der Bahnumläufe, die der Satellit schaffen würde, wenn sich an der aktuellen Situation nichts mehr verändert, zur mittleren Bahnhöhe?
Erstens brauchen wir die Umlaufperiode P. Die erhalten wir, indem wir die Anzahl der Sekunden an einem Tag durch die “Mean Motion” dividieren. Also P=86400/MM. Der Zusammenhang zwischen großer Halbachse a (= mittlerem Bahnradius) und Umlaufperiode P ist (ohne Herleitung): a=21.61355 * P^(2/3). Da ich mir und Ihnen hier die Herleitung schenke (übrigens, sollte Ihnen das nicht passen, schlage ich vor, Sie hören hier auf zu lesen), gehe ich auch nicht auf die physikalischen Größen und Einheiten ein, sondern beschränke mich darauf, Ihnen zu sagen, dass die Bahnperiode in Sekunden eingegeben werden muss und dass die große Halbachse in km herauskommt.
Ja, und die Höhe?
Reingefallen! Die kriegen sie gar nicht. Die Erde ist ein Ellipsoid und die Bahn ist elliptisch und alle Bahnelemente, auch die große Halbachse, sind zudem nur mittlere Bahnelemente. Also ist es beliebig schwierig und nicht besonders aussagekräftig, wollte man nun versuchen, die Bahnhöhe über irgendeinem überflogenen Punkt auf der Erdoberfläche auszurechnen. Die große Halbachse und deren Änderung ist das, was Sie sich anschauen sollten, denn die Bahnenergie hängt nur von diesem Parameter ab – man muss sich also auch nur die große Halbachse anschauen, wenn man verfolgen will, wie die Luftreibung die Bahn absenkt.
In einigermaßen guter Näherung kann man von der großen Halbachse den Äquatorialradius der Erde (6378 km) abziehen und erhält so annähernd die aktuelle Bahnhöhe bei der Äquatorüberquerung, allerdings auch nur dann, wenn die mittlere Exzentrizität der Bahn fast bei 0 liegt.
Wie wäre es mit einem Beispiel?
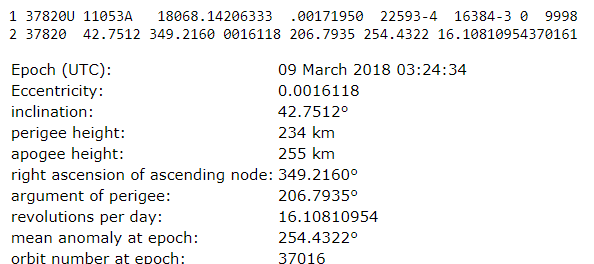
OK, nehmen wir doch mal das Objekt –> hier. Für heute, 9.3.2018, lese ich dort folgende Two Line Elements:
Ich lese dort eine “mean motion” von 16.10810954 Umläufe pro Tag ab. Der numerische Wert zur “first derivative” wäre 0.00171950. Ein positiver Wert, also nimmt die “mean motion” zu,was auch plausibel ist. Durch die langsame Abbremsung und den dadurch bewirkten Abstieg nimmt die Umlaufperiode ab und die Bahngeschwindigkeit zu. Bei sinkender Umlaufperiode passen immer mehr Umläufe in einen Tag. Der Zahlenwert zur “second derivative …” ist 0.22593E-4.
Nur mit der “mean motion”, unter Vernachlässigung der geringen Erhöhung im Verlauf des Tages, ergibt sich eine Umlaufperiode P von 5363.758 s und eine große Halbachse von 6622.8 km. Wenn ich davon den Äquatorradius abziehe, ergibt sich eine ungefähre Höhe von 244.8 km, was recht gut zur angegebenen Perigäums- und Apogäumshöhe passt.


Ich habe mich über die Formel für die Entwicklung der MM gewundert:
(1) MM=MM1+(1/2)*MM2*t+(1/6)*MM3*t²
da ich hier eine Taylorreihe mit den entsprechenden Koeffizienten erwartet hätte, also
(2) MM=mm1+mm2*t+(1/2)*mm3*t² + [ (1/6)*mm4*t³+…]
. Aber auch an anderer Stelle heißt es dass MM2 & MM3 die “first derivative of mean motion […] divided by 2” und “second time derivative in daily mean motion, divided by 6” sind [a]. Warum also diese Koeffizienten?
Unter Annahme dass (2) gilt folgen natürlich folgende Terme für die Ableitungen:
(3) dMM/dt |t=0 = mm2
(4) dMM/dt² |t=0 = mm3
daher dann sollte nach [a] gelten:
(5) MM2=(1/2)*mm2
(6) MM3=(1/6)*mm3
und (2) wird zu
(7) MM=mm1+2*MM2*t+3*MM3*t² + [..]
also auch nicht äquivalent zu (1)…
Meine Vermutung ist folgende:
Die Koeffizienten sind nicht darauf ausgelegt, dass man die MM bestimmt, sondern die Mean Anomaly. Deren Taylor Entwicklung wäre:
(8) MA = MA1 + ma2*t + (1/2)*ma3*t² + (1/6)*ma4*t³+[…]
Wenn jetzt die MM die zeitliche Ableitung der MA ist:
(9) MM=dMA/dt
Würde (8) ergeben:
(10) MA = MA1 + mm1*t + (1/2)*mm2*t² + (1/6)*mm3*t³+[…]
Daher also die Angaben der Werte MM2 & MM3 mit diesen Faktoren:
(11) MA = MA1 + MM1*t + MM2*t² + MM3*t³+[…]
Dies würde aber immer noch bedeuten, dass (1) falsch wäre und (7) müsste stattdessen gelten:
(7) MM=MM1+2*MM2*t+3*MM3*t²
[a] spaceflight.nasa.gov /realdata/sightings/SSapplications/Post/JavaSSOP/SSOP_Help/tle_def.html
Ich würde die Frage nach der Art der Reihenentwicklung nicht überbewerten. TLEs sind ohnehin ein reichlich wackliges Konzept aus der Frühzeit der Raumfahrt. Es hat allein deswegen überlebt, weil es weltweit so viel Software gibt, die auf TLEs aufsetzt.
Bei ganz niedrigen Bahnen, wo der Abstieg selbst von einem Tag auf den nächsten so groß ist, dass er nicht vernachlässigt werden kann, reicht in aller Regel schon die erste Ableitung. Dass z.N. auch die mittlere Exzentrizität sich verändert, wenn die Bahn so stark abgebremst wird, fällt im Konzept der TLEs bereits unter den Tisch, ebenso wie die säkularen Änderungen der anderen Bahnelemente und die nicht zu vernachlässigenden Variationen über einen Umlauf. Das Ganze ist nichts als eine Krücke, mehr nicht.
Anmerkung vom 26.3.2018: Im obigen Artikel wurden die Bahnelemente für das Beispielobjekt für den 9.3.2018 abgerufen. Damals lag die große Halbachse der Bahn bei 6622.8 km. Aus den TLS vom 25.3.2018, also 16 Tage später, berechne ich eine große Halbachse von 6589.0 km. Also hat der mittlere Bahnradius in diesen 16 Tagen um 33.8 km abgenommen – und zwar nicht linear. Ich bitte auch um Beachtung des Rocket Science Blogs der ESA.
Laut TLEs für Tiangong 1 für den 29.3.2018 09:00:36 UTC: Aktuell 16.30342433 Umläufe pro Tag. Große Halbachse der Bahn damit 21.61355 * (86400/16.30342433)^(2/3) = 6469.768 km. Das wären nur noch etwa 191 km über dem Erdäquator, 20 km weniger als noch vor drei Tagen! Jetzt geht es zügig. Mittelwert des Wiedereintrittzeitpunkts laut ESA Rocket Science Blogs ist Sonntag, 1.4.2018 um 00:00 UTC (kein Scherz!).