As this might be of interest to readers who do not speak German, I shall write this post in English. In an earlier blog post I referred to the Ariane 5 ECA launch VA241. This launch delivered its payload of two geostationary payload into a HEO with initial inclination and argument of perigee values of approximately 21 and 231 degrees respectively. This is particularly problematic for the Al Yah 3 satellite which relies on conventional, chemical propulsion for GEO insertion and ion propulsion for the operational phase, while the SES-14 satellite uses low-thrust, high-Isp ion propulsion both for the insertion and for station keeping.

(Author’s Note: All I am providing here is my personal opinion and some results of mathematical calculations I have performed myself based on publicly available information. These results could have been obtained by anyone with a background in orbital dynamics. Nothing I write here shall be construed as reflecting the official position of my employer. Essentially, what we have here is a mathematical problem: A spacecraft is in a given initial orbit and shall reach a certain target orbit B with a certain amount of delta-v. What I am presenting is a mathematical solution to this problem that I have identified. Now, back to the blog article …)

The Earth oblateness is continuously increasing the argument of perigee at a rate of around half a degree per day, which means that the difficulty and cost of reaching the target orbit is exacerbated with every day that passes. I have attempted to compute an optimal three-impulse transfer, starting out from the orbital elements as extracted from the two-line-elements available on Thursday, 1 Feb 2018.

As I am not familiar with the operational constraints that apply to Al Yah 3, e.g.,  concerning pointing directions, I am not applying any such constraints in the optimisation process. Also, for the sake of computational speed, I am assuming manoeuvres to be impulsive and I am not considering orbital perturbations. Therefore, the results I present here should be seen as approximate.

Note that all computations were performed in and all data are given relative to an inertial reference frame which is the Mean Earth Equator frame of the epoch 2018/2/1 0:0:0 DBT.

Here is the summary of the manoeuvre sequence I obtained. The total, impulsive manoeuvre cost is 2168 m/s. Gravity losses and navigation will come on top of that figure.

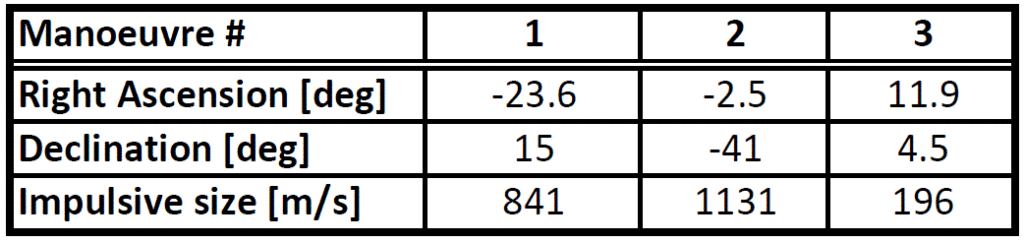
And here is the summary of the orbital element before and after each manoeuvre. Remember – I assume purely Keplerian orbits in this approximate computation.

The following three diagrams illustrate the orbital geometry in the transfer I obtain. I show a 3D view, the a top view, looking don from the North Pole, then a side view, seen from along the Earth equator plane.

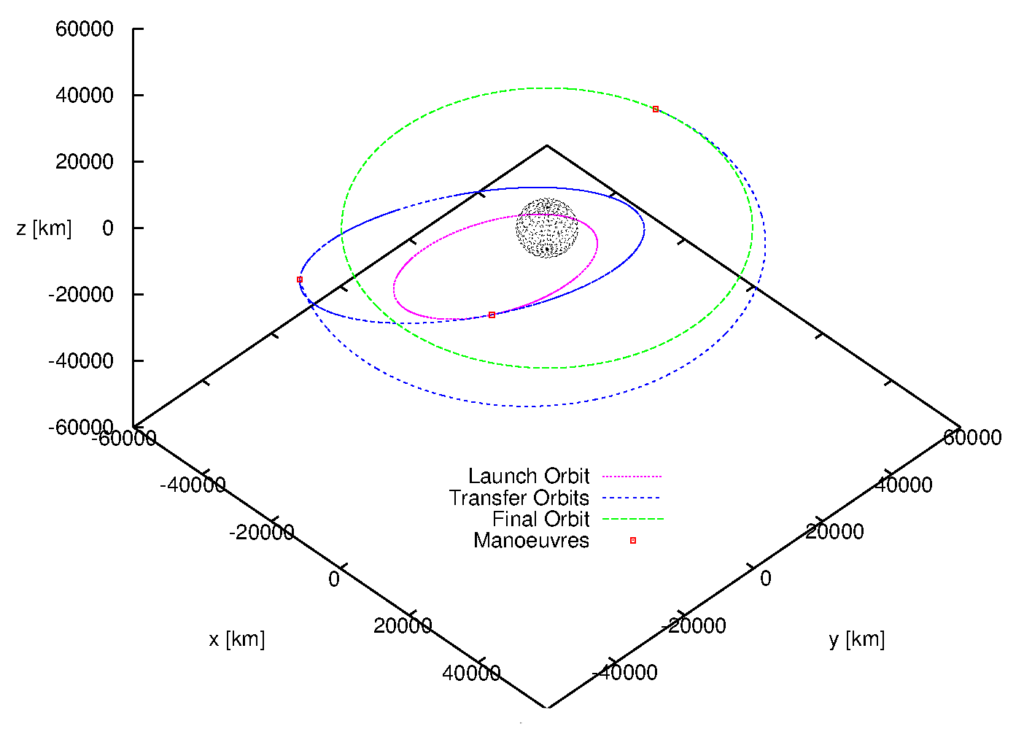
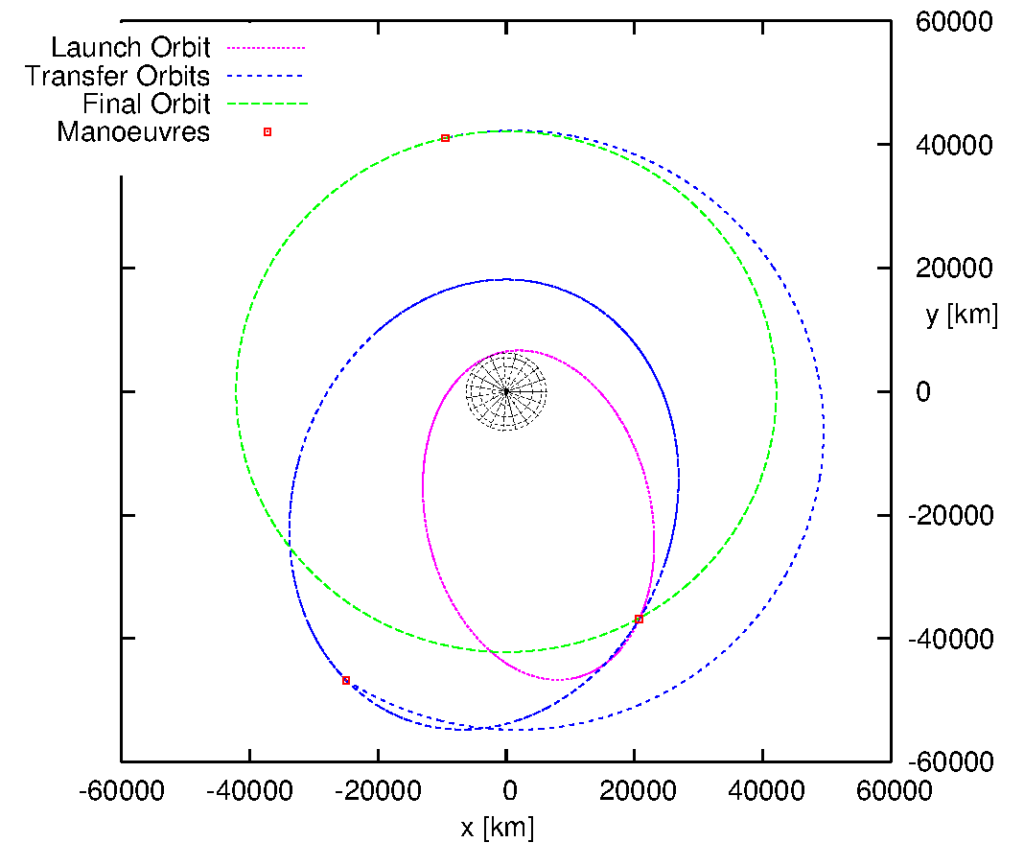
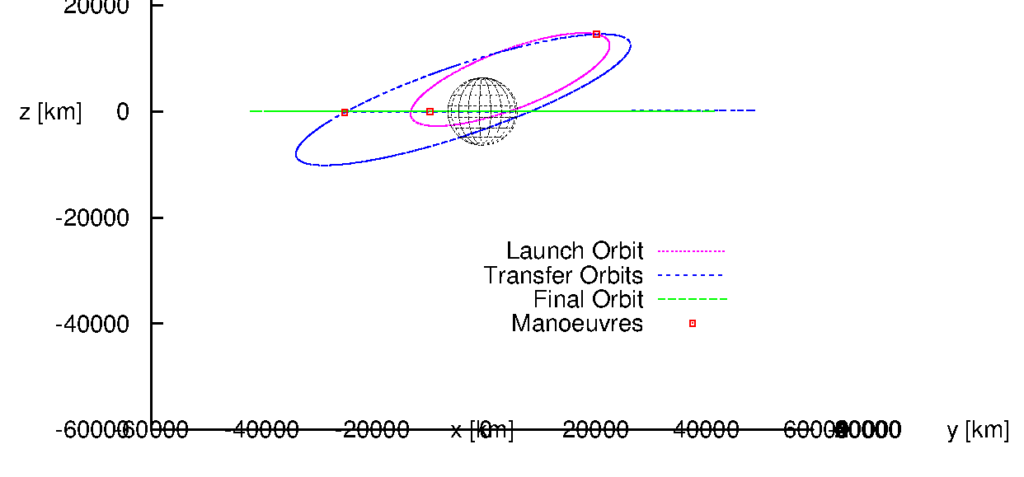
An Afterword

Maybe I missed something important and there is a much better way for Al Yah 3 to reach its target orbit than the one I presented. If so, please let me know.