Eine kleine Denksportaufgabe
BLOG: Fischblog

Als ich gestern Abend unbeschäftigt in der U-Bahn saß – und gerade keine Lust auf die Antworten auf meinen letzten Hot Takes auf Twitter hatte – bin ich auf ein interessantes Schachbrettmuster der Kacheln in einem Bahnhof gestoßen.

Ja, mir war sehr langweilig.
Dabei ist mir folgendes aufgefallen: Beim normalen Schachbrettmuster landet der Springer nach einem Zug immer auf der entgegengesetzten Farbe.

Das Muster im Bahnhof allerdings verhält sich etwas anders. Dort ist die Wahrscheinlichkeit, von einem beliebigen Feld auf der entgegengesetzten Farbe zu landen, nur noch 50 Prozent:
(Kurioserweise kommt man, wenn man die von den vier schwarzen Feldern erreichbaren Felder zusammenzählt, nicht auf 50:50, aber das spielt meiner Meinung nach keine Rolle)
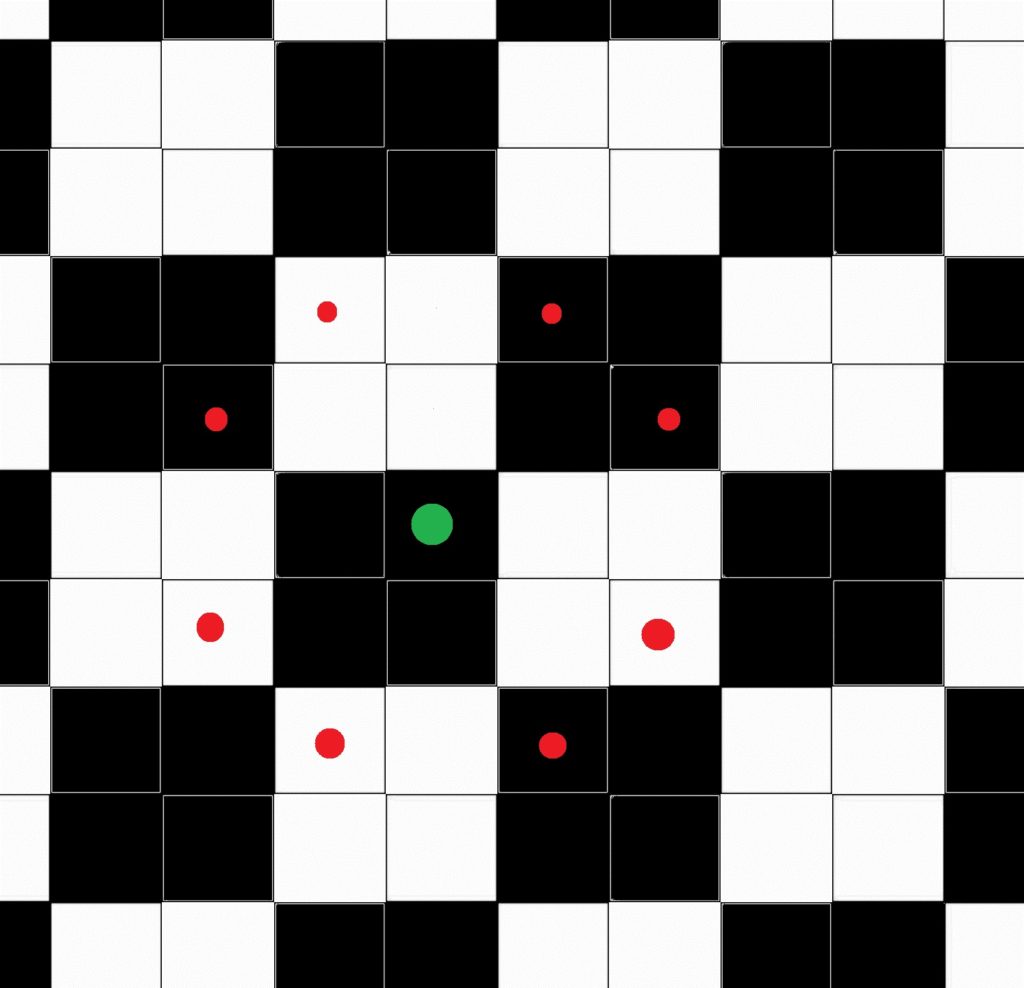
Wieder anders verhält es sich bei n=3. Ich habe die zwei unterschiedlichen Arten von Randfeldern in unterschiedlichen Farben durchgetestet, vom mittleren Feld aus erreicht man augenscheinlich nur die andere Farbe. Die Wahrscheinlichkeit, von einem beliebigen Feld auf der entgegengesetzten Farbe zu landen, ist anscheinend 8/9 · 0,5 + 1/9 · 1 = 5/9 oder etwa 56 Prozent.
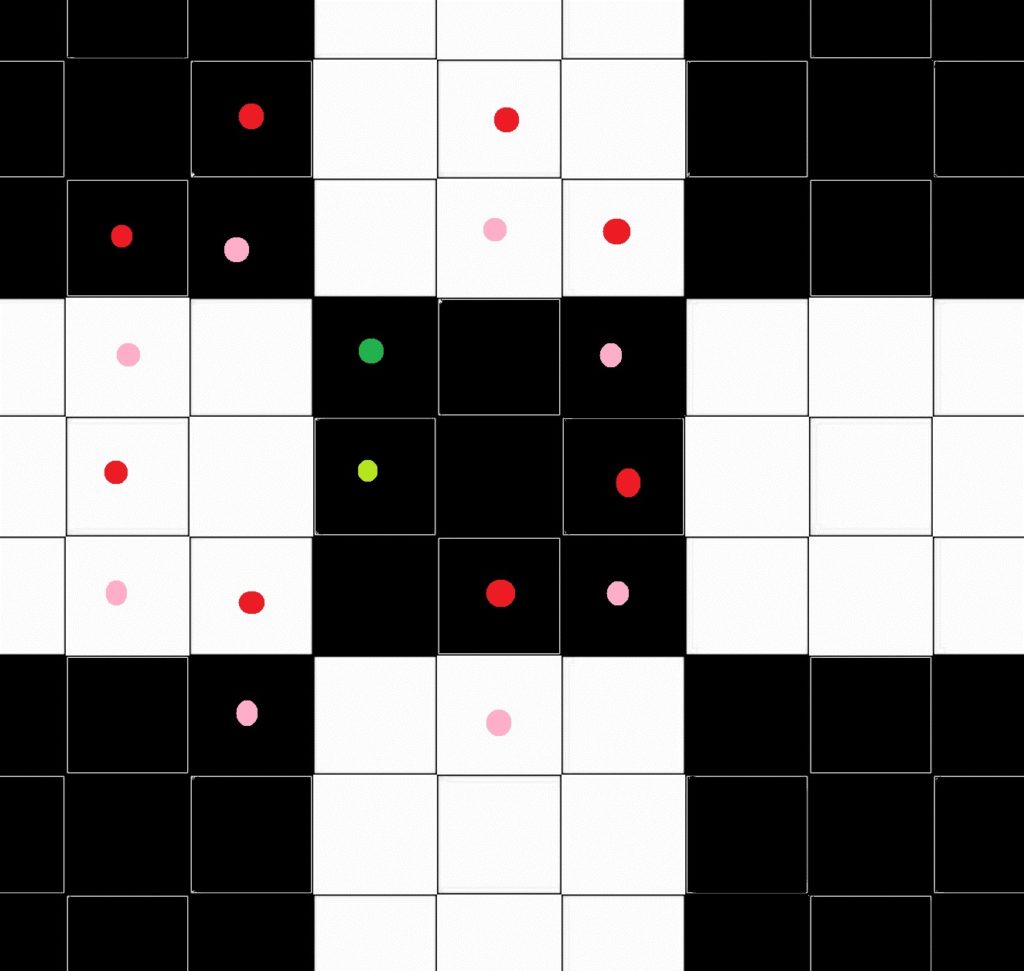
Für n = 4 habe ich das Spielchen nicht durchexerziert, aber zwei Sachen erscheinen mir offensichtlich: Zum Ersten geht die Wahrscheinlichkeit, auf der entgegengesetzten Farbe zu landen, bei sehr großen n gegen Null, weil der Rand einen immer kleineren Anteil der Fläche ausmacht. Zum zweiten sinkt die Wahrscheinlichkeit ab n = 5 kontinuierlich, weil ab hier immer mehr Felder hinzukommen, von denen nur die gleiche Farbe erreichbar ist.
Jetzt frage ich mich:Wie kann man für ein beliebiges n ≥ 5 die Wahrscheinlichkeit berechnen? Kann man das für alle n auf diese Weise machen oder sind 1 bis 4 quasi Außenseiter?
(Alle Bilder: Александр Ковалёв / Stock.adobe.com, verändert von mir)


Ich bin der Sache noch nicht wesentlich näher gekommen, habe aber das Gefühl, dass eine Gleichung (die m.E. für alle n gleich funktionieren sollte) auch die Anzahl der angrenzenden Felder gleicher Farbe beinhalten müsste. Also im falle von n=2 immer 1, bei n=3 entweder 2 oder 4 (bei start im mittleren Feld), etc.
Wie genau das aber gehen soll, bin ich noch nicht sicher 🙂
Mal ganz naiv (nach zwei Bier und ohne Bleistift und Papier)
wenn n >= 4
Du hast n*n Felder einer Farbe. Wie groß ist die Wahrscheinlichkeit dass du bei start von diesen Feldern auf derselben Farbe landest. Du schneidest mal auf allen Seiten einen 2 Felder breiten streifen ab, un betrachtest: das innere Quadrat, die 4 ecken aus je 4 Feldern. Die 4 Seiten streifen die sich in den inneren und äußeren Streifen unterteilen
Für das innere Quadrat (n-4) * (n-4) Felder ist dir Wahrscheinlichkeit 1
Für die Reihen an der Aussenkante dieses inneren quadrates (4 *(n-4)) Felder bleibst du in 6 von 8 Zügen auf der selben Farbe. Also 0.75
Für die Aussenreihe (ausser den 4×4 ecken, also auch 4 * (n-4) Felder) sind das 4 von 8 Zügen: 0.5
Genauso kann man sich die 4×4 ecken ansehen.
4 * 0.5
4 * 0.5
8 * 0.5
Also komme ich insgesamt so auf
P = ((n-4)^2 + 0.75 * 4 * (n-4) + 0.5 * 4 * (n-4) + 16 * 0.5) / (n^2)
Etwas umformen ohne Papier (und eventuell mit Fehlern)
P = ((n-4)^2 + 3 * (n-4) + 2 * (n-4) + 8) / (n^2)
P = ((n-4)(n+1) + 8) / (n^2)
P = (n^2 – 3*n +4) / (n ^ 2)
P = 1 – (3*n + 4) / n^2
Als geht die Wahrscheinlichkeit auf der selben Farbe zu landen wirklich gegen 1
Natürlich ist die letzte Zeile falsch und sollte
P = 1 – (3*n – 4) / n^2
heissen
Für große n kommt, glaube ich, für die Wahrscheinlichkeit, ein Feld anderer Farbe zu treffen,
p(n) = 3(n-1)/n^2
raus. Das sollte ab n>=5 gelten. Ist aber eine schnelle Überlegung gewesen, also bitte mit Vorsicht genießen.
Idee: man muss nur Rand und Felder der zweiten Reihe von außen betrachten. Nur die Ecken der zweiten Reihe haben auch p=1/2, die anderen p=1/4. Rand hat immer p=1/2. Jetzt zusammenzählen und durch n^2 teilen. Wie gesagt, nur schnelle Überlegung, kann also Denkfehler enthalten
Mit einem ähnlichen Ansatz wie Mirko (ich habe die Wahrscheinlichkeit betrachtet, auf einem andersfarbigen Feld zu landen):
A: Der Springer landet von einem beliebigen Feld auf einem andersfarbigen Feld.
P(A)= (3n-4)/n^2 (mit n>=2)
Ich habe also genau die Gegenwahrscheinlichkeit von Mirkos Ergebnis ausgerechnet, die Formel liefert auch für n>=2 die schon im Artikel angesprochenen Werte.
Mirko und Ruben haben natürlich recht. Habe gestern mich beim Abzählen der Felder der zweiten Reihe von außen vertan,
(3n-4)/n^2 ist die Wahrscheinlichkeit für einen Farbwechsel für den Spezialfall eines unendlich großen Schachbretts. Für ein endliches Schachbrett mit der Seitenlänge mn (m Blöcke mit jeweils n gleichfarbigen Feldern) ist die Wahrscheinlichkeit geringer wegen der Eck- und Randfelder:
(3m^2*n – 4m^2 – 3mn + 4m – 12n + 20) / (m^2*n^2 + 32mn – 96)
(Anzahl möglicher Züge mit Farbwechsel)/(Anzahl möglicher Züge gesamt)
d.h. Rand- und Eckfelder werden weniger gewichtet, da es hier nur 2, 3, 4 oder 6 mögliche Züge pro Feld gibt statt 8.
Eine Prüfung in Excel zeigt, dass die allgemeine Funktion für große m gegen die spezielle Funktion konvergiert.
Das Layout der Scilogs hat sich zum Positiven hin entwickelt. Leider werden in den Kommentaren die Links nicht mehr durch Farbe oder Unterstreichung gekennzeichnet. Eine Reparatur wäre angenehm.
testlink
Ein kleines Gedicht zum Thema Mathematik:
MATHEMATIKER
Die Mathematik erfordert Wissen,
Doch nicht als ewiges Ruhekissen.
Für die mathematischen Prozesse
Braucht es Geist und Akkuratesse.
Man erwartet wegweisende Ideen,
Mathematiker müssen vorangeh’n.
Sie lieben Summen und Differenzen
Genauso wie Wurzeln und Potenzen.
Vektorrechnung und Trigonometrie,
Wie auch die Algebra begeistern sie.
Differential,Integral – ganz egal,
Sie beherrschen Infinitesimal.
Sie quadrieren und interpolieren,
Woll’n ständig mit Zahlen jonglieren.
Sie stehn auf Euklid und Pythagoras,
Haben an Logarithmen großen Spaß.
Sie bearbeiten Funktionen versiert,
Die Kurvendiskussion wird geführt.
Extremwerte sind gar kein Problem,
Sie lösen jedes Gleichungssystem.
Sie führen die kniffligsten Beweise,
Berechnen flott Trapeze und Kreise.
Das alles ohne den geringsten Frust,
Mathematik ist ihnen eine Lust.
Rainer Kirmse , Altenburg
Auf was für Ideen man so kommen kann!
Ich hätte diese Unterteilung gar nicht vorgenommen, sondern wäre zunächst davon ausgegangen, dass man einfach keine grösseren Platten zur Verfügung hatte, um die gewünschte Grösse der Schwarzen, bzw. weissen Flächen zu bekommen. Doch dann fällt als weiterer Aspekt die optische Täuschung auf: nämlich der Eindruck, dass die Fugen zwischen den Platten schräg verlaufen oder gar schief sind. Dabei sind tatsächlich zwei verschiedene Plattengrössen verwendet worden. Der Grössenunterschied ist aber recht klein, deshalb fällt er nicht sofort auf.