Wenn es um die Berechnung der Nachkommastellen von Pi geht, ist der Ehrgeiz jedes Zahlentheoretikers geweckt, geht es doch darum möglichste viele und mithilfe des Computers möglichst schnell zu berechnen. Wer hat die schnellsten Prozessoren und die besten Formeln um den neuen Weltrekord aufzustellen? Während sich die Elektroingenieure um die Prozessoren kümmern, widmen sich die Mathematiker den Formeln.

Unendliche konvergierende Reihen und die Nachkommastellen von Pi

Es gibt zahlreiche Formeln um Pi zu berechnen, doch nicht alle eignen sich gleich gut für den Computer. Zum Glück entwickelten Newton und Leibniz zu Beginn des 17. Jahrhunderts die Differenzial- und Integralrechnung und es ergaben sich völlig neue Möglichkeiten zur Berechnung von Pi. Mit Hilfe von unendlichen konvergierenden Reihen berechneten Mathematiker Pi nun wesentlich schneller und auf deutlich mehr Stellen als bisher. Dabei verwendeten sie am häufigsten die Arcustangens-Reihe. Sie hatten herausgefunden, dass für die Tangens-Funktion die folgende Gleichung

Manche dieser Reihen entzücken durch ihre schlichte Eleganz und einfachen Rechenvorschriften.. Von Gottfried Wilhelm Leibniz (1646-1716) stammt die nachfolgende Formel für Pi, die er 1682 fand.

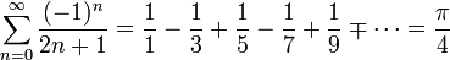
Wie man sieht, beruht sie auf einer unendlichen konvergierenden Reihe, ist leicht zu merken und kommt ohne viel Schnörkel aus

Was aber haltet ihr von dieser Formel, die auch auf einer unendlichen konvergierenden Reihe beruht?

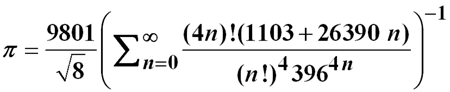
Sie wurde von Srinivasa Ramanujan (1887-1920) entwickelt. Was hatte der geschmissen, als er diese Formel entwickelte? Sie sieht bizarr aus. Die Zahlen, die in dieser Formel verwendet werden, scheinen nach dem Zufallsprinzip ausgewählt worden zu sein. Das stimmt doch nie und nimmer!

Doch der Zahlentheoretiker weiß, dass nicht Äußerlichkeiten zählen sondern innere Werte. 😉

Denn tatsächlich ist es so, dass die Reihe in der Leibniz-Formel ziemlich langsam konvergiert während die Reihe der Ramanujan-Formel mit jedem neuen Reihenglied acht neue Nachkommastellen von Pi liefert. Für die Berechnung von Pi ist Leibnizs Formel also eine Pferdekutsche während Ramanujans Formel ein Ferrari ist. Wie könnte man die Leibniz-Formel schneller machen also sozusagen „frisieren“? Leonhard Euler (1707-1783) hatte die Idee das Konvergenzverhalten dadurch zu verbessern, dass man in den Gleichungen mehrere Arcustangens-Werte verwendet.

Ramanujans Formel beruht auf einem elliptischen Integral, wurde 1910 von ihm entdeckt und 1985 benutzt um 17 Millionen Nachkommastellen von Pi zu berechnen.

Wem solche Formeln zuwider sind und für Verse ein besseres Gedächtnis hat, dem empfehle ich folgenden verschlüsselten Merkvers für die ersten neun Nachkommastellen von Pi.

Wie, o dies π macht ernstlich so vielen viele Müh

Die Anzahl der Buchstaben in jedem Wort, liefert nämlich in der gleichen Reihenfolge die gesuchte Ziffer, d. h. 3,141592653. Wenn Du diese neun Nachkommastellen kennst, heißt das, die Abweichung vom „wahren“ Wert π muss kleiner sein als fünf Zehnmilliardstel. Was ist der praktische Nutzen dieser Rechenakrobatik? Fragt mich nicht…… Es genügen beispielsweise zur Berechnung des Kreisumfangs auf einen Millimeter Genauigkeit

bei einem Radius von 30 Metern: vier Dezimalstellen von Pi,

beim Erdradius: zehn Dezimalstellen,

bei einem Radius mit dem Abstand Erde-Sonne: 15 Dezimalstellen.

Aktuell sind 10 amerikanische Trillionen Dezimalstellen von Pi bekannt. Das ist eine Eins mit 13 Nullen.

„Mangelnde mathematische Bildung zeigt sich am deutlichsten in äußerster Schärfe im Zahlenrechnen.“

Gauß

Rechner, Reihenentwicklung und Rundungsfehler

Computer lieben Reihen und deshalb möchten sie am liebsten gar nicht mehr aufhören zu rechnen und die Zahlen bis zum Sankt-Nimmerleins-Tag durchrattern. Prinzipiell so lange bis der Speicher überläuft. Und da liegt genau das Problem, denn irgendwann muss Schluss sein und wann Schluss ist, muss der Programmierer vorgeben. Da die Zahl der Nachkommastellen, die der Computer zeigt, festgelegt ist, heißt das gleichzeitig er wird den Rundungsfehler vorgeben.

Ich möchte das mal am Beispiel eines alten Taschenrechners mit zehn Stellenanzeigen demonstrieren.

Wir gehen von folgenden zwei Rechnungen aus:

1. ln 98765432 = 18,40825822

2. e^18,40825822 = 98765431,70

Der Unterschied in der letzen Stelle entsteht dadurch, dass der Rechner Y = e^z in die Reihe:

e^z = 1 + x/1! + x²/2! + x³/3! + …+ xⁿ/n! entwickelt.

Wer möchte, kann mal für die Funktion e² diese Reihe für 2, 4, 8 und 16 Reihenglieder entwickeln und schauen, was mit dem Rundungsfehler passiert. Das kann man besonders gut beobachten, wenn man einen Rechner besitzt, dessen Nachkommastellen gewählt werden können.

Übrigens –  wer gerade Langeweile und Rechnerkapazitäten frei hat, kann sich auch mit folgender Formel der Brüder David and Gregory Chudnovsky rumschlagen, ein hässliches Biest.

Sie liefert für jedes Reihenglied 14 Nachkommastellen für Pi. Die größere Herausforderung liegt aber nicht darin den Weltrekord zu brechen indem man mehrere Prozessoren parallel schaltet sondern eine neue und bessere Formel als die der Chudnovsky-Brüder zu finden. Und wenn es diese Formel gibt, bin ich mir sicher, wird es nicht die „Halle Berry“ der unendlichen konvergierenden Reihen sein.

Weiterführende Links

Die Geschichte der Approximationen der Zahl Pi

Zahlwörter: Ich kapier’s einfach nicht!

Warum die ganze Erbsenzählerei?