Giovanni Girolamo Saccheri und die Kammer des Schreckens

Die Geometrie ist ein sehr altes, mehrstöckiges Gedankengebäude: Im Erdgeschoss befindet sich die Planimetrie, die Eigenschaften von zweidimensionalen Grundformen wie Dreiecken, Vierecken und Kreisen untersucht. Hier stand Giovanni Girolamo Saccheri vor der Tür zur Kammer des Schreckens, öffnete sie, doch betrat die Kammer nicht, bestürzt von dem was er dort sah. Dies ist die Geschichte wie er zu dieser Tür gelangte……
Saccheri (* 5. September 1667 – † 25. Oktober 1733 in Mailand) war von 1699 bis 1733 Professor für Mathematik an der Universität in Pavia, Italien und versuchte einige Jahre vor seinem Tod das Parallelenaxiom des Euklids zu beweisen. Er beschrieb die Ergebnisse seiner Bemühungen in der Abhandlung “Euclides ab omni naevo vindicatus (Euklid befreit von jedem Makel) “, die jedoch von seinen mathematischen Zeitgenossen wenig beachtet wurde.

In den Elementen des Euklids (Elemente, Buch 1) findet sich das Parallelenaxiom als das fünfte Postulat:
“Wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirkt, dass innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei Rechte werden, dann müssen die zwei geraden Linien bei Verlängerung ins Unendliche sich auf der Seite treffen, auf der die beiden Winkel liegen, die zusammen kleiner als zwei Rechte sind.“
Im Gegensatz zu den anderen vier Postulaten des Euklids ist dieses besonders lang und kompliziert. Deshalb wurde es schon im Altertum als Makel der euklidischen Axiomatik empfunden. Das Postulat besagt in moderner Formulierung, dass zwei parallele Geraden sich nie treffen.
Mathematiker wie Archimedes (3. Jahrhundert v. Chr.), Ptolemäus (2. Jahrhundert), Thabit ibn Qurra (9. Jahrhundert), Nasir Al-din al-Tusi (13. Jahrhundert) hatten versucht es aus den anderen Postulaten herzuleiten um damit zu zeigen, dass es für die Definition der euklidischen Geometrie entbehrlich ist. Saccheri war also nicht der Erste, der sich versuchte. Neu war jedoch seine Methode: Er wollte das Parallelenaxiom indirekt beweisen.
Ein Mathematiker zeigt bei einem indirekten Beweis (Widerspruchsbeweis), dass ein Widerspruch entsteht, wenn die zu beweisende Behauptung falsch wäre. Dazu nimmt er an, dass die Behauptung falsch ist, und wendet dann die gleichen Methoden wie beim direkten Beweis an. Wenn daraus ein Widerspruch entsteht, dann kann die Behauptung nicht falsch sein, also muss sie richtig sein (Satz vom ausgeschlossenen Dritten). Wichtige (und keinesfalls selbstverständliche!) Voraussetzung für die Gültigkeit eines Widerspruchsbeweises ist, dass im zugrunde liegenden Axiomensystem die Aussage nicht zugleich wahr und falsch sein kann (Widerspruchsfreiheit). Ein klassisches Beispiel eines Widerspruchsbeweises ist der euklidische Beweis dafür, dass es unendlich viele Primzahlen gibt.
Saccheri ging so vor, dass er eine geometrische Aussage suchte, die dem Parallelenaxiom gleichwertig aber einfacher und verständlicher formuliert ist. Er fand sie:
Die Innenwinkelsumme im Dreieck beträgt 180°.
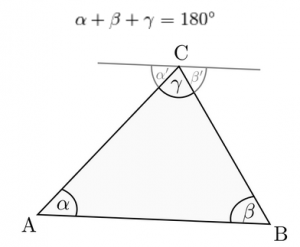
Er wandte seine Widerspruchsbeweis auf diesen Satz an und untersuchte zwei Fälle:
a) Die Innenwinkelsumme im Dreieck ist größer als 180°.
b) Die Innenwinkelsumme im Dreieck ist kleiner als 180°.
Im ersten Fall a) kam er zu der Aussage, dass alle Geraden endlich sind, was Euklids 2. Postulat widersprach. Diese Geometrie, in der Euklids 2. und 5. Postulat nicht gültig sind, ist die sogenannte sphärische Geometrie. Sie begegnet uns, wenn wir die Längen- und Breitengrade auf einem Globus betrachten. Diese Geraden sind hier allerdings Kreise. János Bolyai, Nicolai Ivanovich Lobachevsky, Carl Friedrich Gauss und Georg Friedrich Bernhard Riemann entdeckten die sphärische Geometrie erst im 19. Jahrhundert.
Saccheri hatte also die Hälfte des Weges geschafft und wandte sich nun dem zweiten Fall b) zu. Seine Untersuchungen führten ihn zu Ergebnissen, die zwar absurd schienen aber keinen offensichtlichen Widerspruch ergaben. Er hatte die hyperbolische Geometrie entdeckt. Diese hat ihren Namen daher, dass sie die Geometrie auf einem Rotationshyperboloid ist.
Die “Abscheulichkeit” seiner Ergebnisse interpretierte Saccheri jedoch als Widerspruch zu seinem ästhetischen Empfinden der euklidischen Geometrie und glaubte damit das 5. Postulat bewiesen zu haben.
Das passt zu dem was mein Blogger-Kollege Tobias Maier auf dem Heidelberg Laureate Forum aus einem Gespräch mit dem Mathematiker Michael Atiyah erfuhr:
“When in doubt between truth and beauty, go for beauty. Because you never know if something is actually true.”
Es ist eine tragische Fußnote in der Geschichte der Mathematik, dass Saccheri die von ihm begonnenen Wege nicht weiterging, wie es z. B. der Mathematiker Gerhard Frey beim Versuch des Beweises des letzten Fermatschen Satzes tat. Saccheri hätte einer der berühmtesten Mathematiker werden können.
I shall be telling this with a sigh
Somewhere ages and ages hence:
Two roads diverged in a wood, and I—
I took the one less traveled by,
And that has made all the difference.
Robert Frost, “The Road Not Taken”


Mal davon abgesehen, dass die Sache mit dem ausgeschlossenen Dritten eine zweiwertige logische Axiomatik benötigt, die in erdachten Systemen, in Tautologien, vorliegen kann, nicht aber auf das Weltliche bezogen, bei dem hier wird Ihr Kommentatorenfreund hellhörig:
…denn Schönheit adressiert eine Empfindung, wie sie beim erkennenden Subjekt entstehen könnte, Einfachheit wäre allerdings ähnlich einzustufen, und -wichtiger- wenn ein Mathematiker sich nicht sicher ist auf Grund einer erfolgreich verlaufenen Beweisführung, dass das zu Beweisende wahr [1] ist, dann scheint eine Anomalie vorzuliegen.
MFG
Dr. W
[1]
In der Tautologie ist ‘wahr’ ein Wert (“wie jeder andere”), der typischerweise gewonnen wird, wenn eine Aussage widerspruchsfrei auf eine Axiomatik zurückgeführt werden kann.
Ansonsten könnte er auch zugewiesen werden, was aber hier wohl nicht gemeint ist.
@Dr. Webbaer
Sie haben da scheinbar eine recht privatsprachliche Beziehung zum Wort ‘Tautologie’ geknupft.
Für den logischen Hausgebrauch wird mit Tautologie schlicht eine aussgenlogische Formel bezeichnet, die bei jeder Interpretation den Booleschen Wert TRUE liefert (in der Wahrheitstafel). Also beispielsweise, passend zum Stchwort Widerspruchsbeweis,
(p ∧ (¬q → ¬p)) → q
Bei Ihnen erscheint ‘Tautologie’ indessen als Synonym für ‘formale Sprache’. Ihre sprachlichen Kompositionen zu dechiffrieren fällt manchem hier doch ohnedies schon schwer genug.
@ Chrys :
Philosophie (sofern nicht das Weltliche oder das Sittliche gemeint ist >:-> ), Mathematik und Formalwissenschaft gelten nicht nur für den Schreiber dieser Zeilen als tautologisch, weil sie in Systemen arbeiten deren Realbezug unklar zu bleiben hat, wenn Beweisvorhaben über die Rückführung auf willkürlich bereit gestellte Axiomatiken gelingen.
Aber sehr gut, dass Sie verstanden haben.
Mit Ihnen ist der Schreiber dieser Zeilen, vom Weltlichen und vom Sittlichen einmal abgesehen, außergewöhnlich zufrieden, Sie ergänzen ansonsten und bringen bei.
Darauf, auf Kollege Michael Atiyah, bildlich gesprochen, noch ein wenig herumzutreten, haben Sie keine Lust?
MFG + schönes Wochenende schon einmal,
Dr. W
@Dr. Webbaer Was tautologisch ist, hat Chrys ja schon erklärt. In Bezug auf die absolute Geometrie können sie die Tautologie “Das Parallelenaxiom gilt oder es gilt nicht” formulieren. Der Realbezug dieser Tautologie (Metaaussage) sind dann die speziellen Geometrien, die sie in der Welt vorfinden.
Sie schreiben: “gelten nicht nur für den Schreiber dieser Zeilen” Für wen gilt das namentlich noch? Haben sie irgendeinen Philosophen oder Mathematiker im Sinn, der ihre Auffassung teilt?
Wenn es Ihnen lieber ist, Herr Dr. Dramiga, könnte bei bestimmter Philosophie, der Mathematik und der Formalwissenschaft statt von ‘Tautologien’ von Sprachlichkeiten gesprochen und geschrieben werden, deren Realbezug unklar ist.
Insofern lag bei der Verwendung der Tautologie ein wenig (zudem: von anderen übernommene) Polemik vor, korrekt.
Sie regen an bestimmte von Subjekten erkannte weltliche Bezüge als (teilweise) grundlegend für die Erstellung der Axiomatiken der o.g. Sprachlichkeiten zu verstehen, Dr. W auch hier bei Ihnen.
Der Schreiber dieser Zeilen bleibt bei derartiger Aussage – ‘When in doubt between truth and beauty, go for beauty. Because you never know if something is actually true.’ – unglücklich.
MFG
Dr. W
@ Joe Dramiga
“Für wen gilt das namentlich noch?”
Für Wittgenstein.
6.1 “Die Sätze der Logik sind Tautologien.”
Das kann man für alle axiomatisch aufgebauten Systeme verallgemeinern, damit auch für die Mathematik. Darin sind alle Sätze tautologisch. Man kann mathematische Sätze beweisen, was ja nichts anderes heißt, als sie aus den Axiomen abzuleiten. Axiome und Sätze sind demnach redundant, es liegt immer eine Tautologie vor. Man erkennt dies, wenn man in
(p ∧ (¬q → ¬p)) → q
für p die Gültigkeit der Axiome setzt und für q die Gültigkeit des abgeleiteten Satzes.
Falls man Philosophie, Formalwissenschaften oder vielleicht auch die Physik versuchen würde axiomatisch aufzubauen, gälte das auch für diese.
Was ich hier schreibe, könnte selbst tautologisch sein, wenn auch die Sprache auf Axiomen beruhen würde.
@Joker (Tautologie: schon einmal erwähnt)
Die Wahrheit kann nicht als “logisch” bezeichnet werden, sie ist auch kein Bestandteil des logischen Kalküls. Der Begriff der Wahrheit führt notwendigerweise ad Absurdum, soll er logisch begründet sein.
Genauso wie es unzulässig ist, von einem Weg (x) als “einem einzig wahren” zu sprechen (es ist unzulässig, denn wenn man die exklusive Wahrheit des (x) annimmt, muss man gleichzeitig annehmen, dass andere Wege (y,z) weniger wahr oder gar falsch sind…was wiederum nicht sein kann, denn, wenn angenommen wird, dass jeder Weg “wahr” ist, der zum Ziel führt und wenn angenommen wird, dass es viele völlig unterschiedliche, gar sich ausschliessende, dennoch parallel gültige (valide) Ziele gibt, welche durch andere Wege (y,z) erreicht werden können, dann ist die Exklusivität des Wahrheitsbezugs (x) ungültig)…so ist es unzulässig, dass innerhalb der universellen Logik von “der Wahrheit” als einem logischen Wert (als einem exklusiven Wert) gesprochen wird.
Wir kommen langsam überein, wir.
@Joker
Andersherum geht es vielleicht einfacher.
Es ist nicht ‘tautologisch’, Sätze aus Axiomen abzuleiten. Beweisbare aussagenlogische Formeln heissen auch Sätze oder Theoreme oder Propositionen. Das ist dann eine syntaktische Kategorie, Tautologie ist hingegen eine semantische.
Es ist nicht ‘tautologisch’, Axiome zu setzen. Von Tautologie spricht man im logischen Kontext meines Wissens eigentlich nur a) in der Aussagenlogik oder b) allenfalls bei Ausdrücken, die sich als aussagenlogische Formeln verstehen lassen und als solche dann Tautologien unter a) sind. In diesem Sinne ist die Aussage des Parallelenaxioms dann schlicht ein aussagenlogischer Term, der als TRUE oder FALSE interpretiert werden kann. Das Parallelenaxiom ist gewiss keine Tautologie.
Wittgensteins Statement 6.1 aus dem Tractatus lässt sich so verstehen:
Und so ungefähr steht das dann auch in Logic for Dummies etc.
Jenseits der formalen Logik kann Tautologie auch eine rhetorische Figur meinen. Es mag den etymologischen Neigungen von Dr. Webbaer entsprechen, zwischen den verschiedenen kontextuellen Bedeutungen eine tiefere Beziehung zu vermuten.
@ Chrys
“Andersherum geht es vielleicht einfacher.”
“Es ist nicht ‘tautologisch’, Axiome zu setzen.”
“Es ist nicht ‘tautologisch’, Sätze aus Axiomen abzuleiten.”
Die Tautologie scheint in einem schlechten Ruf zu stehen. Warum eigentlich? Wie klingen in deinen Ohren die Sätze des nächsten Abschnitts?
—
Wenn man den Beweis für einen mathematischen Satz sucht, versucht man nachzuweisen, dass es sich bei Axiomen und dem Satz zusammengenommen um eine Tautologie handelt. Dabei besteht schon der Beweis aus einer Aufeinanderfolge von Tautologien.
Bei den Axiomen versucht man Tautologien zu vermeiden: “Saccheri […] versuchte einige Jahre vor seinem Tod das Parallelenaxiom des Euklids zu beweisen.”, er versuchte nachzuweisen, dass die fünf Axiome des Euklid eine Tautologie sind.
Es ist offensichtlich nicht trivial, zu erkennen, was eine Tautologie ist und was nicht. Erschwerend kommt hinzu, dass es Axiome und Sätze gibt, von denen man das nie wissen wird. Dieser Satz selbst ist zusammen mit den Axiomen eines hinreichend mächtigen formalen Systems allerdings schon wieder eine Tautologie.
—
Woher stammt also die Abneigung? Vielleicht weil der Unterschied “zwischen den verschiedenen kontextuellen Bedeutungen” von Tautologie bei dessen emotionaler Bewertung nicht immer ausreichend berücksichtigt wird?
“Es ist nicht ‘tautologisch’, Axiome zu setzen.”
“Es ist nicht ‘tautologisch’, Sätze aus Axiomen abzuleiten.”
Ja, so ist es. Aber ist das wirklich einfacher, oder klingt das nur einfach freundlicher als “[Logik], Mathematik und Formalwissenschaft gelten […] als tautologisch” ?
@Joker
Du bist heute aber ziemlich anstrengend. 😉
Was Wittgenstein mit ‘Tautologie’ ausdrücken wollte, hat er in einem an Russell gerichteten (und original auf Deutsch verfassten) Brief von 1913 so erläutert:
Dies ist zweifelsfrei auf die Aussagenlogik zu beziehen (und nicht auf irgend sonst eine Logik), und so wird der Begriff dann auch in der Literatur verwendet. Ein Beispiel (J.P. Burgess. Philosophical Logic. PUP, 2009, p.6):
Und testweise noch ein weiteres Beispiel, ebenfalls zur Aussagenlogik, von dem ich nur noch nicht weiss, ob es hier typographisch korrekt dargestellt wird (G. Priest. An Introduction to Non-Classical Logic. CUP, 2nd ed. 2008, p.5):
So schwierig ist es doch wohl nicht, von Tautologie zu reden, ohne dabei sogleich eine Sprachverwirrung anzuzetteln.
Joe Dramiga schrieb (6. September 2015):
> Die Geometrie ist ein sehr altes, mehrstöckiges Gedankengebäude: Im Erdgeschoss befindet sich die Planimetrie […]
Und in seinem Fundament befindet sich der metrische Raum, sowie dessen (noch mehr oder weniger auszubuddelnde) Verallgemeinerungen.
> In den Elementen des Euklids (Elemente, Buch 1) findet sich das Parallelenaxiom als das fünfte Postulat: […] Im Gegensatz zu den anderen vier Postulaten des Euklids ist dieses besonders lang und kompliziert.
Und (der Grundfehler!) es benutzt den Begriff „Winkel“ als handele es sich dabei (schon) um (Zahlen-)Werte, die man ohne weiteres vergleichen und mit denen man ohne weiteres rechnen könne, ohne zu definieren, wie „Winkel“-Werte denn überhaupt gemessen werden sollen.
> Das Postulat besagt in moderner Formulierung, dass zwei parallele Geraden sich nie treffen.
Die (moderne?) Formulierung des Parallelenaxiom (der euklidischen Geometrie) in Wikipedia lautet allerdings auffallend anders.
@Frank Wappler Du schriebst: “Und (der Grundfehler!) es benutzt den Begriff „Winkel“ als handele es sich dabei (schon) um (Zahlen-)Werte, die man ohne weiteres vergleichen und mit denen man ohne weiteres rechnen könne, ohne zu definieren, wie „Winkel“-Werte denn überhaupt gemessen werden sollen.”
Euklid definiert den Winkel statisch als Neigung. David Hilbert hat in seinem Buch “Grundlagen der Geometrie” (1899) die Grundbegriffe wie Punkt, Gerade, Ebene usw. nicht definiert und sie insbesondere nicht als Punkte, Geraden, Ebenen des Anschauungsraum gesehen (Loslösung von der sogenannten “ontologischen Bindung”). Durch die Axiome werden lediglich Beziehungen zwischen den Grundbegriffen festgelegt.
Joe Dramiga schrieb (15. September 2015 15:02):
> David Hilbert hat in seinem Buch “Grundlagen der Geometrie” (1899) die Grundbegriffe wie Punkt, Gerade, Ebene usw. nicht definiert und sie insbesondere nicht als Punkte, Geraden, Ebenen des Anschauungsraum gesehen (Loslösung von der sogenannten “ontologischen Bindung”). Durch die Axiome werden lediglich Beziehungen zwischen den Grundbegriffen festgelegt.
Im Zusammenhang mit Hilberts Festlegungen hinsichtlich „Winkeln“ wurde angemerkt, dass
(Mir ist dabei allerdings nicht ganz offensichtlich, ob es auch dann als „unentbehrlich“ gilt, wenn das Hilbert-Euklidische Parallelenaxiom IV weggelassen wird, oder ob es dann (selbstverständlich) mit wegfällt.)
Wenn ein Mathematiker als Axiom postuliert, dass es zu etwas Bestimmten etwas „Gleiches“ gäbe (siehe alle Hilbertschen „Axiome der Kongruenz (Gruppe III)“), dann fragt man sich als Geometer bzw. als Physiker jedenfalls:
Wie misst man das?
Wie findet man heraus, auf welche bestimmten Anschaulichkeiten das zutrifft?;
sofern es nicht von vornherein auf alle zutreffen soll.
@Frank Wappler Du fragtest: “Wie misst man das?
Wie findet man heraus, auf welche bestimmten Anschaulichkeiten das zutrifft?;
sofern es nicht von vornherein auf alle zutreffen soll.”
Da gebe ich Dir recht, das da Kongruenzaussagen wie z. B. zwei gegebene Strecken sind gleich lang oder zwei bestimmte Winkel haben das gleiche Maß nicht weiterhelfen. Ich weiß nicht wie das mit der Hilbertschen Fassung der Geometrie gelingt.
Jedoch in der von Descartes begründeten analytischen Geometrie (in der viel lineare Algebra und Analysis steckt) gibt es Definitionen von Punkt, Gerade, Ebene, Strecke, Länge, Abstand, Winkel. Auch hier gelten die Axiome von Hilbert/Euklid. Da kann ich es mir vorstellen.
Joe Dramiga schrieb (15. September 2015 23:24):
> Jedoch in der von Descartes begründeten analytischen Geometrie […]
Koordinaten-Streußeleien ?!?
Nein (danke). Wenn schon, denn schon.
@Dr. Abbär: Ha ha ha ha
@Chrys:
(p ∧ (¬q → ¬p)) → q
Ist kein Widerpruchsbeweis, sondern der Beweis der Gültigkeit eines wahrheitslogischen Prinzips (entweder – oder, tertium non datur), denn es besagt entweder p oder q, denn:
(q ∧ (¬q → ¬p)) → p
Schönes WE, Jungs
@Maciej Zasada
Wenn Sie die Brille aufsetzen, dann sehen Sie meine Formel vielleicht als den Satz zum Modus tollens.
Wenn ich die Brille aufsetze, dann sehe ich Ihre Formel als den Ausdruck q → p.
Und wenn Dr. Webbaer die Brille aufsetzt, dann sieht er Ihre Formel hoffentlich nicht als Tautologie.
Ich, lieber Chrys, trage seit einiger Zeit Brille, mehrfach beglast.
Um scharf zu sehen, setze ich sie manchmal ab.
Vor kurzem hat einer unter einem von mir verfassten Artikel “geliked” und ich ging auf seine Seite, um zu sehen, wer er ist. Ich sah, dass er kürzlich einen engagierten Artikel “An alle Nazis” schrieb, der sich deutlich gegen die Adressaten richtete. Ich dachte mir komm, setz doch “gefällt mir” drunter… doch dann kam mir ein anderer Gedanke: ich kann nicht mehr “für” oder “gegen” sein. Diese Zeit ist vorbei. Jetzt bin ich alles und Alle.
Denn ich kenne keine Wahrheit, außer der, die, unter all den behaupteten Wahrheiten, mit sich selbst identisch ist.
Verstehen Sie, Chrys?
Ob mit oder ohne Brille, ich fürchte, ich verstehe nicht.
Und? Soll ich jetzt im Karre springen?
@Alle (bevor der Schwachsinn endgültig die Oberhand gewinnt)
“Die Sätze der Logik sind Tautologien.”
Gemeint ist, dass Sätze der Logik, um gültige Sätze der Logik zu sein, notwendigerweise wahr sein müssen (denn ex falso quodlibet – bildlich gesprochen: die falschen Sätze können, aber nicht müssen logisch sein, um wahrhaftig und tatsächlich falsch zu sein – sie sind aus Prinzip an keine Logik gebunden).
Daher, wenn “die Wahrheit” als das Kriterium der Existenz im logischen Raum angenommen wird, müssen die gültige Sätze der Logik Tautologien sein.
In der Wahrheitslogik entscheiden wir die Existenz p anhand der Wahrheit von p (es ist p, wenn es auch wahr ist, dass p)
Innerhalb der Universallogik entscheiden wir die Existenz von p anhand der Selbstidentität (p = p).
https://perspektivenlogik.wordpress.com/2015/08/14/universallogik-gesetz-der-identitaet/
https://perspektivenlogik.wordpress.com/2015/08/25/universallogik-das-gesetz-der-existenz/
Die unsägliche Verbindung der Wahrheit mit der Logik ist die Anfangsbedingung der Wahrheitslogik. Die Wahrheit gibt der Logik einen Sinn (Richtung).
Die Logik darf jedoch keinen Sinn besitzen. Die Logik ist sinnfrei (die Logik ist das gesamte Strassennetz, keine konkrete Verbindung zwischen A und B)
Das, was wir “Logik” nennen ist daher in Wirklichkeit eine logische Anwendung, die uns beispielsweise ermöglicht, das Wahre, das Schöne, das Gute von ihren jeweiligen Gegensätzen zu unterscheiden.
Es ist Einfach.
Man muss unterscheiden zwischen einer formalen und einer materialen Logik. Die formale Logik arbeitet mit bedeutungsfreien Symbolen. Aussagen der formalen Logik sind dann wahr, wenn sie aus Axiomen, Definitionen oder Vorannahmen logisch korrekt abgeleitet werden können. Die Wahrheit hat dann keine empirische, sondern nur formale Bedeutung bezüglich der Prämissen.
Die materiale Logik bezieht sich auf die sprachliche Bedeutung der verwendeten Begriffe. Zusätzlich kann man unterscheiden zwischen einer polaren, zweiwertigen oder absoluten Logik, in der das “tertium non datur” gültig ist und andererseits einer unpolaren, mehrwertigen oder relativen Logik, in der dieses ungültig ist. Aussagen oder Sätze haben dann empirische Bedeutung und können also durch Beobachtung oder Erfahrung in der realen Welt bestätigt oder widerlegt werden, abhängig von der sprachlich kommensurablen Bedeutung oder Definition der Begriffe. Hier hat der Begriff der Wahrheit seine klassische Bedeutung: p ist dann wahr, wenn p (semantisch, empirisch) gültig ist.
Ein wesentliches Merkmal logischer Schlussfolgerungen ist, dass sie keine neue oder zusätzliche Information hervorbringen! Solche Schlussfolgerungen können aber zu neuen Überlegungen, Forschungen, Perspektivänderungen, Umformulierungen, Entdeckungen oder Experimenten Anlass geben und somit indirekt neue Information und Wissen erzeugen.
“Aussagen der formalen Logik sind dann wahr, wenn sie […] logisch korrekt abgeleitet werden können.”
Hier dreht es sich im Kreis, mir wird schwindlig.
Das hat Wittgenstein gesehen und @ Marcej Zasada hat versucht, uns dies zu erklären.
Gegen Schwindel gibt es Mittelchen. Wahrheit bezieht sich immer nur auf die Prämissen, egal ob in einem formalen Symbolsystem oder in der realen, materialen Welt der sprachlichen Begriffe. Die Schwierigkeiten in der materialen Welt ergeben sich aus dem Verständnis bzw. Missverständnis in der genauen Bedeutung verwendeter Begriffe und der Unvollständigkeit der Sprache. Eine korrekt angewandte Logik erzeugt keine Tautologien, sonst wäre die Logik insgesamt völlig nutzlos. Tautologie bedeutet, dass eine Aussage immer wahr ist, nichts anderes. Sie bezieht sich also nicht auf die logische Schlussfolgerung selber, hat also mehr mit Linguistik als mit Logik zu tun!
@ Anton Reutlinger
“Wahrheit bezieht sich immer nur auf die Prämissen” (A)
“Tautologie bedeutet, dass eine Aussage immer wahr ist” (B)
Da eine wahre Aussage, die mittels einer korrekt angewandten Logik erzeugt wurde, bezüglich ihrer Prämissen wahr ist, und Wahrheit sich immer nur auf diese Prämissen bezieht (A), ist eine wahre Aussage immer wahr, was bedeutet, sie ist eine Tautologie (B) .
Oder kurz: Eine korrekt angewandte Logik erzeugt eine Tautologie.
Das scheint mir ein Widerspruch zu sein zu, “Eine korrekt angewandte Logik erzeugt keine Tautologien”.
Gehen Sie oder ich von falschen Prämissen aus, wenden Sie oder ich die Logik nicht korrekt an oder gilt hier das ausgeschlossene Dritte?
Stillschweigend gehen Sie von wahren Prämissen aus! Die Annahme ist zwar berechtigt, aber man darf sie nicht ignorieren. Wenn aus wahren Prämissen die Logik korrekt angewandt wird, dann entstehen wahre Aussagen bezüglich der Prämissen. Das ist der Sinn und Zweck der Logik und hat mit Tautologie nichts zu tun.
Eine Tautologie entsteht beispielsweise immer dann, wenn man eine Definition umdreht. Aus der Definition “A ist B mit der Eigenschaft p” entsteht die Tautologie “B mit der Eigenschaft p ist A”. Es wäre ganz egal, welche Werte für A und B jeweils eingesetzt würden.
@ Anton Reutlinger
“Wenn aus wahren Prämissen […]”
Ist “wahre Prämisse” nicht eine Tautologie?
Aus “A” folgt doch logisch korrekt, wegen “A→ A”, und “Wahrheit bezieht sich immer nur auf die Prämissen”,”A ist wahr” (bezüglich “A”). Kurz: wenn A eine Prämisse ist, dann ist sie auch wahr.
(Ich hatte weiter oben “von falschen Prämissen” geschrieben, das tut mir Leid und bitte diesen Fehler zu entschuldigen. Ich hätte schreiben müssen, “Gehen Sie oder ich von unterschiedlichen Prämissen aus “.)
In den Naturwissenschaften wird eine Hypothese als Prämisse angenommen. Daraus werden Aussagen als logische Schlussfolgerungen abgeleitet, die nach Möglichkeit empirisch überprüfbar sind. Wenn die Aussage dadurch widerlegt wird, dann ist auch die Hypothese als Prämisse widerlegt.
Wenn man als Prämissen Axiome oder Definitionen wählt, dann kann man wohl von deren Wahrheit oder Richtigkeit ausgehen, denn alles andere wäre Unsinn. Auch dies hat jedoch nichts mit Tautologien zu tun. Man denke an die Axiome Euklids und die Erkenntnisse der Geometrie, die daraus abgeleitet wurden. Sind das etwa Tautologien?
@ Herr Reutlinger :
Dieser Satz könnte für die Naturwissenschaften gelten – ‘When in doubt between truth and beauty, go for beauty. Because you never know if something is actually true.’ – wobei die gemeinte Schönheit Occam’s Razor nicht fern steht.
Allerdings wird in den Naturwissenschaften nicht mit dem Wahrheitsbegriff hantiert (‘when in doubt between truth and beauty’) und im Bereich bestimmter Sprachlichkeit (bestimmte Philosophie, Mathematik & Formalwissenschaft), die nichts mit der Natur direkt zu tun hat, macht die Aussage ebenfalls keinen Sinn, denn dort ist sicher, dass etwas (‘Because you never know if something is actually true.’) tatsächlich wahr ist.
MFG
Dr. W (der hauptsächlich deshalb hier kommentarisch vorstellig geworden ist)
@Dr.Webbaer;
Kein Widerspruch; die Problematik des Wahrheitsbegriffs ist mir bekannt. Man kann ihn aber auch nicht vermeiden. Eine Diskussion darüber würde hier allerdings zu weit führen. Formallogisch würde man besser von Richtigkeit oder Korrektheit sprechen, während die Relativität oder Subjektivität empirischer Wahrheit hinlänglich bekannt ist. Gerade deshalb erscheint mir die Unterscheidung von formaler und materialer Logik so wichtig, also bedeutungsfreie Symbolsysteme gegen bedeutungstragende Begriffssysteme der realen, materialen Welt. Das Wort “material” ist hier nicht im Sinne physikalischer Materie gemeint, sondern umfasst alles Denkbare, Wahrnehmbare und Erfahrbare. Auch die Mathematik ist demzufolge aus einer formalen und einer materialen Perspektive zu sehen.
Wie gerade dieser Blog zeigt, führt die Vermischung immer wieder zu Missverständnissen. Ein schönes Beispiel dafür, über das ich zufällig gerade gelesen habe, lieferte der Mathematiker Hermann Graßmann mit seiner “Ausdehnungstheorie”, aus deren Formalisierung er einen Vorläufer der Vektoralgebra entwickelte. Graßmann fand jedoch keine Anerkennung, weil die Bedeutung seiner Arbeiten damals nicht erkannt wurde! Erst zum Ende seines Lebens (1877) fand er die verdiente Anerkennung durch Fachkollegen.
@Dr.Webbaer Sie schrieben: “…..denn dort ist sicher, dass etwas (‘Because you never know if something is actually true.’) tatsächlich wahr ist. ”
Nein, auch in der Mathematik wird mit Vermutungen so gearbeitet, als wären sie wahre Prämissen. Es wird also auch dort auf wackligen Füßen gebaut.
@Joker “Insofern sich Sätze der Mathematik auf die Wirklichkeit beziehen, sind sie nicht sicher, und insofern sie sicher sind, beziehen sie sich nicht auf die Wirklichkeit.” Albert Einstein
Ich denke Einstein’s Zitat ist da näher an Dr. Webbaer’s Aussagen als Wittgenstein’s 6.1 aus dem Traktatus.
Liest sich ganz gut, werter Herr Zasada, ‘Tautologie’ scheint aber in diesem Zusammenhang ein Reizwort zu sein und wird womöglich nicht benötigt.
MFG + Grüße in den Bruderstaat, insgesamt sehr erfrischend die hiesige Kommentatorik,
Dr. W
Grüße zurück. Mir gefällt hier auch außerordentlich.
mz
@Dr. W
@Chrys
@Anton Reutlinger
@Joe Dramiga (Hallo, es freut mich hier sein zu dürfen)
@ Joker
“Über Tautologien zu sprechen, ohne Verwirrung zu stiften”…
Gestaltet sich schwierig.
Wenn die Eigenschaft der Gültigen Sätze der Logik Ordnung ist, dann ist die ordnende Kraft darin die Wahrheit (und Falschheit die Unordnung stiftende, womit gegen die Gültigkeit der Sätze verstoßen)
Wenn also die gültigen Sätze der Logik Tautologien sind, dann bedeutet das im Umkehrschluss, dass jeder gültige Satz der Logik prinzipiell wahr ist und dass es nur von der Wahrheit der Prämissen abhängig ist, ob seine Wahrheit eine Tatsache ist.
Problem:
(¡) Die Sätze der Logik beinhalten keine Prämissen (!)
Die Sätze der Logik unterscheiden sich von den Sätzen der Alltagssprache darin, dass sie keine Information transportieren.
Ein Satz der Logik beinhaltet die reine Form, keinen semantischen Inhalt.
Sobald Prämissen ins Spiel kommen (um beispielsweise die Wahrheit /die Falschheit eines Satzes anschaulich zu machen) haben wir nicht mehr mit Sätzen der Logik, sondern mit Sätzen der Alltagssprache zu tun (wenn wir diese für Sätze der Logik halten, machen wir denselben Fehler (überspitzt), als wenn wir die beschreibende Sprache eines Musikkritikers, den Klängen des ausführenden Orchesters gleichsetzen – anhand der beschreibenden Sprache ist kein einziger Orchesterton rekonstruierbar).
Darin sehe ich den Grund der Verwirrung (Kategoriefehler). Darin sehe ich auch die prinzipielle Schwierigkeit, die tautologische Form in den Sätzen der Logik zu erkennen. Darin sehe ich aber auch die Notwendigkeit über diese Form eindeutig zu entscheiden (Wittgenstein).
Wenn man Logik betreibt, sollte man klar sehen. Ist die Sicht getrübt wird einem schwindlig.
Prämisse: jedem Wohnort W ist eine Postleitzahl PLZ eindeutig zugeordnet.
Dann gilt: PLZ = a –> W = b. Aus der PLZ a kann auf den Wohnort b geschlossen werden. Durch die Implikation wird keine neue Information erzeugt, denn diese steckt schon in der Prämisse, d.h. im Verzeichnis der Postleitzahlen. Da die Zuordnung der Postleitzahlen nicht isomorph ist (keine 1:1-Zuordnung), gibt es keine Äquivalenz, sondern nur eine einfache Implikation. Wenn man a ändert, ohne b entsprechend zu ändern, wird die Implikation falsch. Eine Tautologie ist weit und breit nicht in Sicht.
Die formale Logik arbeitet mit bedeutungsfreien, bzw. abstrakt definierten Symbolen, insbesondere Zahlen, Mengen und geometrischen Elementen. Außer den Axiomen/Definitionen und den Regeln der Logik ist kein weiteres Wissen nötig. Deshalb kann sie vom Computer ausgeführt werden, als maschinelles Beweisen in der Künstlichen Intelligenz. Die formale Logik gehört daher zur Mathematik, während die materiale, semantisch orientierte Logik wie das Beispiel oben, mehr zur (Sprach)Philosophie gehört, mit Anwendungen in den Naturwissenschaften. Selbstverständlich bildet die formale Logik das unverzichtbare Grundgerüst für die materiale Logik.
Die materiale Logik ist nicht notwendig zweiwertig. Schon der Wahrheitswert “unbekannt” oder “ungewiss” ist hier einzubeziehen! Jeder Mensch hat ein Geburtsdatum, das für viele Zwecke und Entscheidungen der Bürokratie abgefragt werden muss, aber nicht jeder Mensch hat eine Telefonnummer. In Datenbanken gibt es dafür den definierten Defaultwert, weil das Binärsystem des Computers keinen speziellen Wert vorsieht.
@ Herr Reutlinger :
Es gibt tatsächlich eine ‘materiale Logik’, wie eine Recherche ergab, die Trefferzahl war eher gering, aber immerhin.
Ansonsten plädiert Ihr Kommentatorenfreund dafür Welt und Bearbeitung, Außen- und Innenwelt sozusagen, in etwa so zu unterscheiden, wie bspw. von Herrn Zasada beworben, intensiv beworben, >:-> .
Die Innenwelt erkennender Subjekte setzt auf Methoden, Sprachlichkeiten oder Logik, wobei die Unterscheidung zwischen Innen- und Außenwelt nicht einfach fällt, sondern definitorisch zu handhaben bleibt, u.a. Philip K. Dick hat hier ein wenig geforscht oder “geforscht”, nun, zumindest: publiziert.
MFG
Dr. W
PS:
Relationale moderne Datenhaltung kennt hier den Default-Wert ‘Null‘, der das Nicht-Erfasste meint.
Jede “anständige” moderne Datenhaltung zumindest implementiert demzufolge die dreiwertige Logik, auch weil sich bestimmte Defaultwerte wie bspw. 0 für Ertrag nicht bewährt haben, >:-> .
Allerdings kann auch im Unbekannten sinnhaft unterschieden werden, “Rummy” wusste bspw. wie folgt sinnhaft zu erörtern:
-> https://de.wikipedia.org/wiki/There_are_known_knowns
D.h. es könnte auch hier aufgefächert werden.
BTW, Binärsystem, so wie zitiert, meinen (erst einmal nur) “0” oder “1”.
Chrys schrieb (13. September 2015 23:41):
> In diesem Sinne ist die Aussage des Parallelenaxioms dann schlicht ein aussagenlogischer Term, der als TRUE oder FALSE interpretiert werden kann. Das Parallelenaxiom ist gewiss keine Tautologie.
Trifft das wohl (auch) auf die Aussage zu,
,
die Joe Dramiga (6. September 2015) als „ Das Postulat […] in moderner Formulierung“ unterbreitet hat?
@Frank Wappler
Mir scheint, da hat einer gut aufgepasst. Das Adjektiv ‘parallel’ beinhaltet bereits als Prämisse, dass zwei als parallel bezeichnete Geraden g und h entweder zusammenfallen, g = h, oder sich nie treffen, g ∩ h = ∅.
War das der Stein des Anstosses?
@Frank Wappler Parallele Geraden sind entweder identisch oder punktfremd und in einer Ebene gelegen. Im Fall der Identität kann man in dem Fall noch von zwei Geraden sprechen?
Die Parallelität zweier Geraden in der Ebene lässt sich durch deren Punktfremdheit definieren. In diesem Fall sind parallele Geraden per definitionem voneinander verschieden, jedoch ist Parallelität dann keine Äquivalenzrelation. Alternativ lässt sich Parallelität so festlegen, dass die Gleichheit zweier paralleler Geraden nicht trivialerweise ausgeschlossen ist.
Wie soll man es also machen? Nun, die zweite Variante ist die elegantere, siehe dazu Is Parallelism an Equivalence Relation?
@Chrys Wias meinst Du mit “gleich”? Für mich wäre 3 + 2 = 5 “gleich” aber nicht identisch wohingegen 5 = 5 “gleich” und identisch ist. Aber Mathematiker denken vielleicht ganz was anderes und ich bin auf dem Holzweg.
@Joe Dramiga
Gemeint war Gleichheit von Geraden als Gleichheit von Punktmengen in der Ebene.
Klärungsbedürftig ist aber weniger die Gleichheit als die Parallelität von Geraden, weil letztere auch in der Literatur nicht einheitlich definiert wird. Genauer, ist eine Gerade parallel zu sich selbst?
Fur meinen Geschmack ja, denn das ist schöner so. Geschickter ist es dabei noch, das Pferd andersrum aufzuzäumen und zuerst Nichtparallelität von Geraden zu bestimmen. Etwa so:
Def. 1: Zwei Geraden g, h, in der Ebene sollen transversal heissen, wenn sie sich in genau einem Punkt schneiden, d.h., wenn ein eindeutig bestimmter Punkt P existiert, sodass g ∩ h = {P}.
Def. 2 (Parallelität): Zwei Geraden g, h, in der Ebene sollen parallel heissen, wenn sie nicht transversal sind.
Und jetzt kommt der Clou:
Axiom (Parallelenaxiom): Parallelität ist transitiv.
Voilà, was will man mehr? Mit den geeigneten Begriffen ist es dann weder besonders lang noch kompliziert.
Chrys schrieb (16. September 2015 11:19):
> […] Und jetzt kommt der Clou: Axiom (Parallelenaxiom): Parallelität ist transitiv.
Schließt das die „elliptische Geometrie“ nicht eher ein, als aus?
p.s. Das abgeschlossene philosophische Traktat:
Ein (identisch) Selbes ist nicht das Selbe wie verschiedene Gleiche.
@maciej zasada
Die Selbstidentität schliesst Gleichheit, somit Parallelität aus.
Wo die Gültigkeit der Form gefordert wird, dort kann nicht in Modellen gedacht werden.
@Frank Wappler
Zur Äquivalenz des Axioms mit Playfair’s Axiom siehe obigen Link, und letzteres ist wiederum nichts anderes als Euklids Axiom bei Hilbert:
Die Existenz einer zu g parallelen Geraden g’ durch P kann Hilbert aus seinen übrigen Axiomen konstruktiv herleiten; das führt er u.a. vor in The Foundations of Geometry, §10.
Chrys (16. September 2015 21:44):
> Die Existenz einer zu g parallelen Geraden g’ durch P kann Hilbert aus seinen übrigen Axiomen konstruktiv herleiten; das führt er u.a. vor in The Foundations of Geometry, §10. [ www dot gutenberg dot org / ebooks / 17384 ]
Ich finde Hilberts Darstellung im Moment schwer zu folgen …
Viel eher komme ich mit einem bekannten Modell der elliptischen Geometrie zurecht:
„Großkreise einer (Euklidischen) Kugel interpretiert als Geraden des elliptischen Raumes“.
Mit Blick auf die oben vorgeschlagenen Definitionen von „Transversalität“ und „Parallelität“
– jeder einzelne Großkreis hat alle (d.h. „sehr viele“) Punkte mit sich selbst gemeinsam
(wird „elliptisch interpretiert“ als:
jede Gerade hat alle (d.h. „sehr viele“) Punkte mit sich selbst gemeinsam;
jede Gerade ist sich selbst gegenüber nicht „transversal“; also
jede Gerade ist sich selbst gegenüber „parallel“.);
– jedes Paar verschiedener Großkreise hat genau zwei Schnittpunkte
(wird „elliptisch interpretiert“ als:
jedes Paar von verschiedenen Geraden hat genau einen gemeinsamen Punkt;
jedes Paar von verschiedenen Geraden ist „transversal“ zueinander;
es gibt kein Paar verschiedener Geraden, die zueinander „parallel wären).
Sofern all das stimmt, erfüllt diese „Parallelitäts“-Beziehung die Definition einer transitiven Beziehung?
Oder warum nicht?
@Frank Wappler
»Viel eher komme ich mit einem bekannten Modell der elliptischen Geometrie zurecht:«
Elliptische Geometrie wird schon durch Hilberts Axiome der Inzidenz, Kongruenz, und Anordnung ausgeschlossen. Genauer gesagt, auch Euklid konnte bereits ohne Verwendung seines Parallelenaxioms zu einer gegebenen Geraden g durch einen nicht auf dieser liegenden Punkt P eine zu g parallele Gerade g’ konstruieren, weshalb dann, wie im Blogartikel beschrieben, Saccheri einen Widerspruch finden konnte.
Eine nur auf den genannten Hilbertschen Axiomen beruhende Geometrie wird bisweilen auch Hilbert-Ebene genannt. Die war hier stillschweigend vorausgesetzt, und Playfair’s Axiom macht dann den Unterschied zwischen Euklidischer und hyperbolischer Ebene aus. Grosskreise auf der Sphäre, die sich transversal schneiden, tun das schliesslich auch nicht in genau einem Punkt, mein obiges ‘transversal’ passt somit nur zur Hilbert-Ebene.
Chrys schrieb (17. September 2015 15:19):
> Elliptische Geometrie wird schon durch Hilberts Axiome der Inzidenz, Kongruenz, und Anordnung ausgeschlossen. […] war hier stillschweigend vorausgesetzt
Ach so. (Wie schade …)
Ich hätte übrigens Hilberts
für besonders (ver-)hinderlich gehalten;
aber Wikipedia präsentiert eine externe Referenz (Benno Klotzek: “Euklidische und nichteuklidische Elementargeometrien”), der offenbar zu entnehmen ist, dass es beim Ausschluss der elliptischen Geometrie durch Hilberts Axiome eher um die Gesamtheit der Kongruenzaxiome (III) geht.
> Grosskreise auf der Sphäre, die sich transversal schneiden, tun das schliesslich auch nicht in genau einem Punkt
Zum Gesamtmodell, gemäß dem Großkreise als “Geraden der elliptischen Geometrie” zu interpretieren sind, gehört (natürlich) auch, die beiden (antipodalen) Schnittpunkte zweier Großkreise als genau einen gemeinsamen “Punkt” zweier “Geraden“ aufzufassen.
(Aber gerade das scheint sich ja mit dem “Anordnungsaxiom II.3” besonders zu beißen.)
> Genauer gesagt, auch Euklid konnte bereits ohne Verwendung seines Parallelenaxioms zu einer gegebenen Geraden g durch einen nicht auf dieser liegenden Punkt P eine zu g parallele Gerade g’ konstruieren,
Euklid zeigte jedenfalls (“Proposition 31”), wie eine (ziemlich) bestimmte Gerade g’ durch P, und in bestimmter Beziehung zu Gerade g, zu konstruieren ist.
Die Konstruktion kann sicherlich auch “in elliptischer Geometrie” ausgeführt werden (dabei erhält man aber keine “Parallele zu g”; bzw. sofern die Konstruktion dann nicht mehr zu einem eindeutigen Ergebnis führt: keinesfalls eine “Parallele zu g”).
@Frank Wappler
Zur Konstruktion, man fälle das Lot von P auf g und errichte bei P die Senkrechte g’ zur Lotgeraden h. Falls g und g’ transversal sind, existiert ein gemeinsamer Schnittpunkt S ∉ h, und es lässt sich ein zweiter, davon verschiedener durch Spiegelung von S an h finden. Sofern sich transversale Geraden genau einmal schneiden, ist das ein Widerspruch, und folglich sind g und g’ parallel. In der Hilbert Ebene kommt das hin, aber eben nicht auf der Sphäre.
Chrys schrieb (18. September 2015 8:10):
> Zur Konstruktion, man fälle das Lot von P auf g und errichte bei P die Senkrechte g’ zur Lotgeraden h
Man kann sich schon zusammenreimen, welche konstruktiven Schritte damit im Einzelnen gemeint sind.
(Das entspricht nur nicht genau der in “Proposition 31” angegebenen Konstruktion, auf die ich mich im vorausgegangenen Kommentar bezog, und die ich deshalb zumindest als Memo schon verlinkt hatte).
> Falls g und g’ transversal sind, existiert ein gemeinsamer Schnittpunkt S ∉ h,
Schön: falls g und g’ (genau) einen gemeinsamen (schnitt-)Punkt haben, dann wollen wir sie “(zueinander) transversal” nennen.
(Btw.: Sofern P ein gegebener Punkt sein soll, der nicht zur gegebenen Geraden g gehört, was üblicher Weise mehr oder weniger deutlich vorausgesetzt ist, ist P jedenfalls kein Schnittpunkt von g und g’. (Die angegebene Konstruktion soll aber vermutlich sicherstellen, dass P zur konstruierten Geraden g’ gehört.))
Aus der Konstruktion an sich geht allerdings nicht hervor, ob und (falls so) wie viele Schnittpunkte g und g’ haben.
Falls sich nun (eventuell wider Erwarten) tatsächlich (mindestens) ein Schnittpunkt S von g und g’ finden ließ (konkret: indem man das konstruierte Segment der Geraden g’ zumindest in eine Richtung so weit verlängerte, bis man den Schnittpunkt S mit g erreichte) …
> und es lässt sich ein zweiter, davon verschiedener durch Spiegelung von S an h finden.
Ist das etwa garantiert??
(Was bedeutet “Spiegelung? …)
> […] In der Hilbert Ebene kommt das hin, aber eben nicht auf der Sphäre.
Hmm …
Eines gebe ich jedenfalls zu:
Ich war bisher in der Vorstellung befangen (und anhand der betrachteten Konstruktionen durchaus hingeleitet) mir einzubilden, dass “in der elliptischen Geometrie” (bzw. in den entsprechend interpretierten Modellen) zwei verschiedene “Geraden” nicht nur unbedingt einen Schnittpunkt gemeinsam haben, sondern gern (oder vielleicht sogar genau) zwei Schnittpunkte (oder vielleicht auch mehr).
Aber offensichtlich gibt es für zwei verschiedene Großkreise auf einer Kugel nur **genau ein Paar** antipodaler Punkte. In der “elliptischen Interpretation” ergibt das demnach auch nur genau einen gemeinsamen “(Schnitt-)Punkt” der beiden verschiedenen “Geraden“.
Ich muss mich also von meiner o.g. Vorstellung verabschieden, und/oder mich nicht so ganz auf das schon mehrfach erwähnte Modell verlassen …
@Frank Wappler
»In der “elliptischen Interpretation” ergibt das demnach auch nur genau einen gemeinsamen “(Schnitt-)Punkt” der beiden verschiedenen “Geraden”.«
Die Gerade h zerteilt die Hilbert Ebene in zwei disjunkte Halbebenen, die durch Spiegelung an h kongruent aufeinander abgebildet werden, sodass dabei genau die Punkte auf h Fixpunkte sind. (Das ist durch die 13 Axiome der Hilbert Ebene so garantiert.) Da der Schnittpunkt S nicht auf h liegt, ist S verschieden vom Spiegelpunkt S*, da die beiden in verschiedenen Halbebenen liegen, also S* ≠ S. Im elliptischen Fall, wo antipodale Punkte identifiziert werden, wäre hingegen S ∉ h und S* = S. Die elliptische Ebene wird nicht durch eine Gerade in zwei disjunkte Halbebenen zerlegt.
Chrys schrieb (18. September 2015 13:25):
> Die Gerade h zerteilt die Hilbert Ebene in zwei disjunkte Halbebenen, […]
> Die elliptische Ebene wird nicht durch eine Gerade in zwei disjunkte Halbebenen zerlegt.
So weit, so gut.
(Obwohl: um keine neuen Begriffe verwenden zu müssen, könnte man wohl sagen, dass ein Geraden-Segment, das h schneidet (so wie man es in der Konstruktion tatsächlich erhalten würde)
– in der Hilbert-Ebene an beiden Enden unbegrenzt verlängert werden kann, ohne wieder auf Punkte des gegebenen Segments zu treffen (oder auf Punkte der im Verlaufe des Verlängerns gefundenen Segmente, oder auf Punkte der gegebenen Geraden h); während es
– in der “elliptischen Ebene beim Verlängern, egal an welchem Ende, wieder getroffen und nachgezogen wird”, sofern man dabei überhaupt von “ungegrenztem Verlängern” reden kann.
)
> Die Gerade h zerteilt die Hilbert Ebene in zwei disjunkte Halbebenen, die durch Spiegelung an h kongruent aufeinander abgebildet werden, sodass dabei genau die Punkte auf h Fixpunkte sind.
Kommt sicherlich darauf an, was unter “Spiegelung” zu verstehen wäre.
(Ich weiß z.B. nicht, dass der Fall ausgeschlossen wäre, in der die eine Halbebene “euklidisch”, die andere aber “hyperbolisch” ist.)
Im Übrigen steht das Fundament des “metrischen Raumes” (einschl. geeigneter Verallgemeinerungen) zur Verfügung, um Begriffe wie “Ebene” oder (auch zunächst überhaupt) “Oberfläche” zu definieren.
@Frank Wappler
»Kommt sicherlich darauf an, was unter “Spiegelung” zu verstehen wäre.«
Hier war stets die Rede von “Spiegelung an einer Geraden”, in Germania auch als Achsenspiegelung bekannt und als solche gemeinhin eindeutig identifizierbar. Kennen Physiker noch andere Arten von Achsenspiegelung?
Zu bemerken ist allerdings, dass diese Konstruktion eigentlich nur in der Hilbert Ebene gelingt. In der elliptische Ebene führt der Versuch, Spiegelung an einer gegebenen Geraden zu definieren, auf einen zusätzlichen Fixpunkt “am Pol”, der nicht auf der Geraden liegt. Und heuristisch kommt dann eine (geeignet modifiziert definierte) Spiegelung an der Geraden als eine Drehung um den polaren Fixpunkt heraus, die antipodale Punkte ineinander überführt. Hieraus lässt sich bereits ersehen, dass elliptische Geometrie signifikant anders ist als die der Hilbert Ebene, auch ohne das Parallelenaxiom zu bemühen.
Sei g eine Gerade in der Ebene E (Hilbert oder elliptisch), dann lässt sich eine von g begrenzte Halbebene definieren als eine maximale konvexe Teilmenge H ⊂ E \ g. Aus den Axiomen der Hilbert Ebene lässt sich herleiten, dass für ein solches H dann E \ g = H ∪ H* gilt, wobei H* die Spiegelung von H an g sei. In der elliptischen Ebene lassen sich indessen je zwei Punkte auch in E \ g noch immer durch eine in E \ g liegende Strecke verbinden. Eine Gerade in der Hilbert Ebene hat folglich zwei verschiedene Seiten und begrenzt zwei disjunkte Halbebenen, eine Gerade in der elliptischen Ebene hat hingegen nur eine Seite.
Chrys schrieb (20. September 2015 11:52):
> Sei g eine Gerade in der Ebene E (Hilbert oder elliptisch), dann lässt sich eine von g begrenzte Halbebene definieren als eine maximale konvexe Teilmenge H ⊂ E \ g. Aus den Axiomen der Hilbert Ebene lässt sich herleiten, dass für ein solches H dann E \ g = H ∪ H* gilt, wobei H* die Spiegelung von H an g sei. […]
> Hier war stets die Rede von “Spiegelung an einer Geraden” […] gemeinhin eindeutig identifizierbar.
Mich interessiert, ob es (auch) garantiert ist, dass H &cup g und H* &cup g insgesamt isometrisch aufeinander abgebildet werden. (Und dabei natürlich die jeweilige Teilmenge g identisch zu sich selbst.)
(Weder kann ich erkennen, dass das in der angegebenen Definition von “Achsenspiegelung” gefordert wäre; noch, wie sich das im Detail aus den Axiomen der Hilbert Ebene herleiten ließe.)
p.s.
“⊂” wird dargestellt as “⊂”.
@Frank Wappler
»Mich interessiert, ob es (auch) garantiert ist, dass H ∪ g und H* ∪ g insgesamt isometrisch aufeinander abgebildet werden.«
Tatsächlich lässt sich jede Bewegung (Isometrie) der Ebene durch Spiegelungen an Geraden erzeugen. Ausgehend von Hilberts Axiomen wird das e.g. alles sehr schön demonstriert von Marvin Greenberg in einem Buch, das als Referenz 20 in dem hier erhältlichen Artikel aufgeführt ist. Schlaueres fällt mir jetzt aus dem Stand dazu nicht ein.
subset — da war ich anscheinend geistig im TeX-Mode. Eine andere und möglicherweise missverständliche Schlamperei ist mir noch aufgefallen: Hinsichtlich der erwähnten Drehung hätte es heissen sollen: “… die antipodale Punkte der Geraden ineinander überführt”. Oder anders gesagt, es wird um 180° gedreht mit dem Pol als Fixpunkt.
Chrys schrieb (21. September 2015 11:31):
> alles sehr schön demonstriert von Marvin Greenberg in einem Buch, das als Referenz 20 in dem hier [ http://www.maa.org/sites/default/files/pdf/upload_library/22/Ford/Greenberg2011.pdf ] erhältlichen Artikel aufgeführt ist.
Zumindest findet sich da schwarz auf weiß das „Uniformity Theorem“ (p. 208), durch das der oben angesprochene Fall ausgeschlossen wird, dass „die eine Halbebene “euklidisch”, die andere aber “hyperbolisch” “ sei.
Also vielen Dank für die Auskunft.
Es bleibt allerdings festzuhalten, dass Oberflächen, die schlicht und einfach durch die Distanzverhältnisse ihrer Bestandteile untereinander charakterisiert sind, nicht unbedingt „uniform“ (auschließlich „flach“, oder ausschließlich „hyperbolisch“; oder auch ausschließlich „elliptisch“) sein müssten.
p.s.
> […] da war ich anscheinend geistig im TeX-Mode
Me, too.
Kleiner Test, ob LaTeX-Rendering Kommentaren immer noch nicht automatisch zugestanden wird:
„\ ( \cup \ (“ wird dargestellt als „\( \cup \)“.
Darüber ließe sich eine philosophische Abhandlung schreiben. Ist die Mittellinie auf einem Fußballfeld eine einzige Gerade, oder sind es zwei, je eine für jede Mannschaft? Vielleicht genügt aber eine einfache Überlegung. Ich meine, es kommt auf den ontologischen Status an. Physikalische, identische Objekte sind an Raum und Zeit gekoppelt, haben außer ihren identischen Eigenschaften jeweils einen Zustand, z.B. Bewegung, anhand deren man sie identifizieren könnte. Bei abstrakten, identischen Objekten sind nur die Eigenschaften der Objekte wesentlich. Deshalb sind sie weder unterscheidbar noch identifizierbar. Es würde sich also um eine einzige Gerade handeln. Wenn die Geraden aber dargestellt oder gezeichnet werden, dann sind es physikalische Objekte! Dann hätte man denselben Fall, als wenn man physikalische Objekte hintereinander anordnen würde.
@ Joe Dramiga
“Im Fall der Identität kann man in dem Fall noch von zwei Geraden sprechen?”
Ja, man kann das. Das funktioniert wenn man zwei Variablen benutzt, diese mit ein und derselben Geraden belegt, und dann sagt: g = h, die beiden Geraden (!) g und h sind identisch. Das ist dann allerdings ein bisschen semantisch gekürzt, das erlaubt uns die Sprache, nicht unbedingt die Logik. Also eigentlich: Nein, man kann das nicht.
Man vergleiche auch den ähnlich gelagerten Fall von Morgenstern und Abendstern.
“Für mich wäre 3 + 2 = 5 “gleich” aber nicht identisch wohingegen 5 = 5 “gleich” und identisch ist.”
Sowohl “gleich”, “identisch” als auch “dasselbe” benötigen in der Regel zwei Valenzen. Ich unterstelle Du möchtest eine Relation zwischen der linken Seite der Gleichung und der jeweiligen rechten ausdrücken. Dann hängt es davon ab, ob Du eine Relation zwischen den Termen, den einzelnen Zeichen, den verwendeten Symbolen oder den repräsentierten Werten bezeichnen möchtest. Vermutlich beziehst Du dich einmal auf die Werte, die sind in deinen Worten jeweils gleich, und das andere mal auf die Symbole, die sind einmal identisch (linkes und rechtes Zeichen sind gleich), einmal nicht.
Wenn man die Gleichung 3 + 2 = 4 + 1 vorliest, könnte man für das Gleichheitszeichen sagen “ist gleich” oder “ist dasselbe wie”.
Ich meine, es ist gleich, was man hier benutzt, da gleich und dasselbe hier dasselbe meinen.
Chrys schrieb (15. September 2015 11:03):
> Mir scheint, da hat einer gut aufgepasst. […]
Man übt sein Beizeisen eben dort, wo sich (wenigstens noch) Anstöße geben lassen.
(Auch wenn’s nicht unbedingt auf den ersten Schlag gelingt …)
p.s. hinsichtlich „formal“ und „material“ usw.:
Um fragen und Fall für Fall bewerten zu können, ob
⟨ Âψ| ψ⟩ ⟨ ψ| Â ψ⟩
und
⟨ ψ| ψ⟩ ⟨ Âψ| Acirc; ψ⟩
einander gleich wären, oder nicht,
braucht man nun mal sowohl „“ als auch „ψ“ (und ‘ne Tastatur).
Ich rate mal mit.
Vielleicht ist es auch wichtig, sich der Existenz solcher Parallelen zu versichern, möglichst in definierter Zahl (eins), wenn´s durch einen bestimmten Punkt gehen soll.
Joker schrieb (15. September 2015 12:14):
> Vielleicht ist es auch wichtig, sich der Existenz solcher Parallelen zu versichern […]
Genau das meinte ich; das geht der im SciLog-Beitrag präsentierten vermeintlichen „ modernen Formulierung des Parallelenaxiom“ offenbar ab.
Joe Dramiga scheint diesen Makel allerdings zu übersehen …
Meinen Sie PLZ = a –> W = b ist ein gültiger Satz der Logik? Nein. Dann wovon sprechen wir?
(PLZ = a –> W = b) ist bereits eine Anwendung eines logischen Gesetzes (nämlich A ∧ (A→B) ⇒ B, oder schlicht A→B), die einem bestimmten (vollkommen austauschbaren) Zweck dient (nämlich die Wahrheit der Prämissen, anhand der angenommenen und tautologisch kodierten Wahrheit des logischen Gesetzes, zu entscheiden / zu bestimmen). Die gültigen Sätze der Logik, wie die Logik selbst besitzen keinen Zweck.
(A ∧ (A→B) ⇒ B) ist ein gültiger Satz der Logik. Eine Tautologie.
PLZ = a –> W = b ist kein gültiger Satz der Logik (deshalb hängt seine Wahrheit von der Wahrheit der Variablen PLZ und W ab).
Im gültigen Satz der Logik spielt der Wahrheitswert (und die Prämissenkodierung) der einzelnen Variablen keine Rolle, die Wahrheit des Satzes ist in seiner logischen Form tautologisch geprägt.
“Die formale Logik gehört daher zur Mathematik, während die materiale, semantisch orientierte Logik wie das Beispiel oben, mehr zur (Sprach)Philosophie gehört”
Es gibt die Eine Logik. Sie gehört nirgends, denn sie steht über allem, was man über sie und Dank ihr ausdrücken kann. (Die Mathematik gehört zur Logik, denn die komplexeste mathematische Gleichung, dem einfachsten logischen Gesetz entsprechen muss)
@Alle
Der Unterschied zwischen einem beliebigen (arithmetischen, geometrischen, mathematischen) System, dessen Gültigkeit durch Axiome (axiomatische Sätze) initiiert wird und Logik besteht darin, dass die Gültigkeit der Logik durch sich selbst beweisende, wahre Sätze – Tautologien – initiiert wird.
Im Beispiel:
A ∧ (A→B) ⇒ B
beweist der Ausdruck (A→B) den Ausdruck A [∧ (A→B)] ⇒ B.
Dadurch unterscheidet sich Logik von der logischen Anwendung, dass wir in der logischen Anwendung (wie der Wahrheitslogik oder Aussagenlogik) zwar mit den tautologischen Sätzen der Logik operieren, doch mit dem Zweck, sie als Gültigkeitsmuster zu verwenden, welche indirekt die logische Gültigkeit von nichtlogischen Prämissen, Theoremen, Ausdrücken, Termini beweisen / widerlegen…entscheiden.
Hierin wird unser Problem entschieden:
Log1: A ∧ (A→B) ⇒ B
Theorem: A=a, B=b
Es ist wahr, dass a: b ∧ (b→a) ⇒ a, denn Log1
Es ist wahr, dass b: a ∧ (a→b) ⇒ b, denn Log1
Es ist wahr, dass ¬a: ¬b ∧ (¬b→¬a) ⇒ ¬a, denn Log1
Es ist wahr, dass ¬b: ¬a ∧ (¬a→¬b) ⇒ ¬b, denn Log1
Von unserer deprimierenden Ignoranz geblendet, unterliegen wir dem Eindruck, wir operierten bereits innerhalb der Logik, während wir bloß und höchstens in der Lage sind, mechanische Vergleiche anzustellen, zwischen der Wirklichkeit und ihrem idealen Abbild.
Danke, Herr Reutlinger. Dank Ihnen verstand ich es selbst.
@ Herr Zasada :
In etwa so, wie Dr. Spock gelegentlich im falschen Moment ‘Logisch!’ gesagt hat, wenn er die Folgerichtigkeit meinte, die physikalische Theorie anbot bis nahelegte.
SCNR
Dr. W
@Dr. W
Vielleicht.
1. Den Unterschied, den Herr Reutlinger innerhalb der Logik platziert, sehe ich persönlich darin, wie wir selbst funktionieren (wir existieren und funktionieren im Logischen, keine Frage) und wie unsere “Logik” (also das, was wir für Logik halten, was allerdings unsere Erfindung ist) funktioniert.
In dem Augenblick, in dem Wir uns bemühen etwas zu verstehen, verlieren wir den Faden…
Wie bei dem Spruch “ich weiß, was Zeit ist, wenn ich nicht danach Gefragt werde, ich weiß es nicht, sobald ich sie erklären muss” (oder so ähnlich)
2. “Mit dem Titel “Stoicheia” erinnert Euklid aus Alexandria (ca. -323 bis -283) an das Wort für Buchstaben, womit die Mathematik gemeint ist, die Buchstaben verwendet, für die Ziffern auf einem Maßstab nur Beispiele sind.” Fußnote Edition Opera-Platons 2010
3. Um gewisse Probleme zu lösen, müssen wir ganz “in Form” sein. Keine Angst davor haben, keinen halt zu haben (so wie es uns gute Musiker vormachen – wie Sviatoslav Richter mal sagte: “spielen muss wie fliegen sein”) – der an Noten denkt, die kommen mögen, der spielt nicht…Musik sind nicht Noten, springen ist nicht die Latte, die es zu überwinden gilt und nicht die Anzahl der Schritte, die dazu notwendig sind….übrigens, die Vögel, die springen am Höchsten!
MfG
mz
@ Herr Zasada :
In etwa so wie auf die Gesamtheit der erkennenden Subjekte, die Naturwissenschaft ist ja Veranstaltung, die sich um Erkenntnis bemüht. wobei Erkanntes, Sachen und Sachbezüge meinend, in “n:m”-Beziehungen (das Fachwort) zwischen Erkenntnissubjekten und eben Sachen und Sachverhalten verwaltet oder zumindest verstanden werden können, von ‘Theorienfrechheit’ (Ihr Duktus) gesprochen oder geschrieben werden kann, zu beachten hier insbesondere die empirische Lage, kann in der Logik beliebig entwickelt werden, sofern die Kohärenz gewahrt bleibt, Wahres wahr sozusagen, wobei es sogar Ausnahmen gibt, Gödel und so, wenn erdachte Systeme nicht mehr ganz mit ihren Axiomatiken zusammenpassen.
MFG
Dr. W
*
“n:m”-Beziehung
**
Wahres wahr bleibt sozusagen
“Theoriefrechheit” ist gut. Erklärt aber nichts – Wittgenstein hat auch gegen Popper gepöbelt (verständlicherweise :)) )
Auf Ihrer Stelle würde ich statt von Logik, die beliebig entwickelt werden kann, von Dialektik sprechen.
Wie bereits genannt, Ihr Duktus, Herr Zasada :
-> https://scilogs.spektrum.de/quantenwelt/lichtgrenze/#comment-19568
Dialektik Gesprächskunst, hier steckt auch die Zwei drinnen,
MFG
Dr. W (der das mit dem ‘frech’ schon ganz OK fand, ansonsten dazu einlädt die hiesige Diskursreihenfolge zu beachten)
War nicht ernst gemeint, aber schön, dass Sie verstanden haben.