80 Jahre Collatz-Vermutung: Let’s play!
Die Collatz-Vermutung ist eine Vermutung über Zahlenfolgen, die 1937 von dem Mathematiker Lothar Collatz geäußert wurde. Er konstruierte diese Zahlenfolgen nach einem einfachen Bildungsgesetz:
1. Denk Dir eine natürliche Zahl
2. Falls die Zahl gerade ist, teile sie durch 2.
3. Falls sie ungerade ist, multipliziere sie mit 3 und addiere 1.
Ich nehme z. B. die 11 und konstruiere mit obigem Bildungsgesetz folgende Zahlenfolge:
11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1 …….
Die Collatz-Vermutung lautet:
Jede so konstruierte Zahlenfolge mündet in den Zyklus 4, 2, 1, egal, mit welcher natürlichen Zahl man beginnt.
Die Mathematiker haben bisher keine Gegenbeispiele gefunden. Es gibt zwei verschiedene Typen von Gegenbeispielen.
Typ 1: Eine natürliche Zahl, deren Zahlenfolge gegen unendlich wächst
Typ 2: Eine natürliche Zahl, deren Zahlenfolge in einen anderen Zyklus als 4, 2, 1 mündet.
Die Vermutung ist aber auch noch nicht bewiesen.
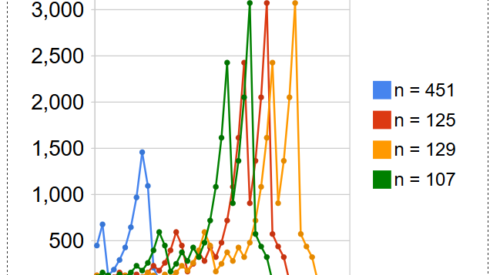
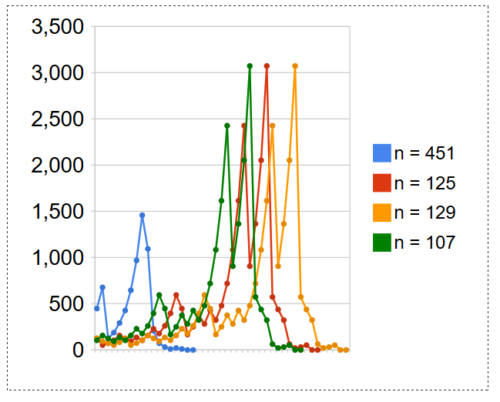
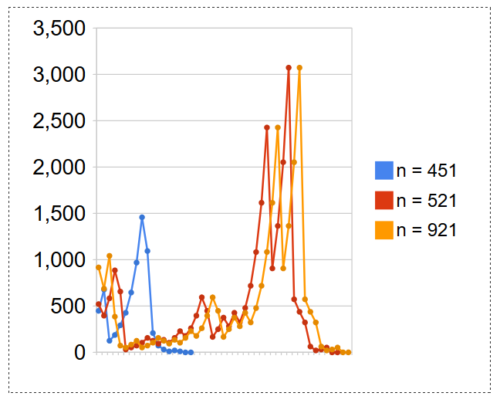
Wenn man die Zahlenfolgen in einem Koordinatensystem visualisiert, zeigen deren Verläufe charakteristische Muster. Haben Zahlen, deren Zahlenfolgen das gleiche Muster zeigen, weitere mathematische Eigenschaften gemeinsam? Im ersten Graph gezeigt am Beispiel des Zahlentripels 107, 125, 129 und im zweiten Graph gezeigt am Beispiel des Zahlenpaars 521, 529.
Eine Erläuterung zu allen folgenden Graphen: Die Graphen beginnen links mit n und enden rechts mit 1. Der Zyklus 4, 2, 1 wird ausgespart. Die Graphen zeigen zwischen n und 1 nur die ungeraden Zahlen der Zahlenfolgen.
An die Mathematiker unter den Lesern, bitte erleuchtet uns, falls das der Fall ist!
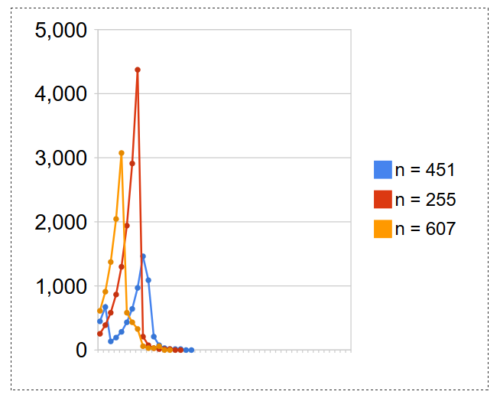
Was hat es mit den Zahlen auf sich, deren Zahlenfolgen zueinander spiegelsymmetrische Muster zeigen? Hier gezeigt am Beispiel der Zahlen 63 und 1279. (Das ist natürlich kein perfektes Beispiel wegen der Skalierung und anderen Dingen, aber ihr versteht, worauf ich hinaus will. Vielleicht findet ja einer von Euch ein besseres Beispiel.) Auch diese Frage geht an die Mathematiker.

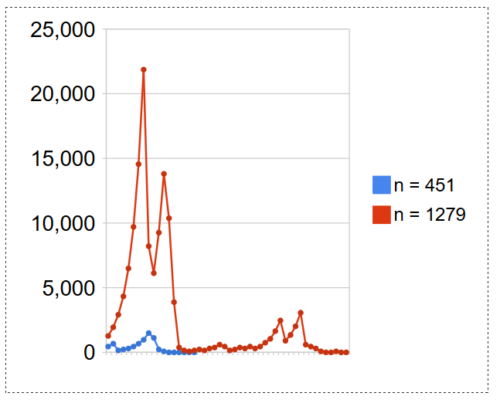
Den Rest lade ich auf die Spielwiese für große Mädchen und Jungs ein ;-).
Wer findet natürliche Zahlenpaare, Zahlentripel, (vielleicht sogar Zahlenquadrupel) mit neuem Muster oder Zahlenpaare mit zueinander spiegelsymmetrischen Mustern?
Bitte in den Kommentarspalten melden!
Hier geht’s zum Muster finden → Collatz-Vermutung-Muster-Finder


Die Collatz-Vermutung ist auch als Ulamfolge bekannt, nach Stanislaw Ulam (1909-1984).
Hier der Versuch eines Teilbeweises:
Sei a eine Zweierpotenz, dann gilt in einem Intervall [a-1,a,a+1]:
a 3n und entweder a+1 = 3n oder a-1 = 3n.
Daraus folgt (a+1)(a-1) = 3n oder a² -1 = 3n oder a²+1 = 3n für alle k>0.
Es gibt also zu jedem k ein n, so dass 3n + 1 = a². Das ist der letzte Teilschritt im Algorithmus.
Es bleibt noch zu beweisen, dass der Algorithmus nicht in einen unendlichen Zyklus mündet.
Ich verstehe deinen Versuch eines Teilbeweises überhaupt nicht, bin aber auch kein Mathematiker. Da kommen Zweierpotenzen, Intervalle und Quadratzahlen vor aber ich sehe nicht den Bezug zum Bildungsgesetz der Collatz-Vermutung. Jedenfalls denke ich, dass ein Beweis sehr schwierig ist, sonst hätten sich Mathematiker nicht 80 Jahre lang die Zähne daran ausgebissen.
@Joe Dramiga;
Auch ich bin kein Mathematiker, deshalb schreibe ich keine mathematischen Blogs. Leider kenne ich auch die mathematische Notation dieses Blogs zu wenig, um mathematische Formulierungen sauber darstellen zu können. Mein Versuch eines Teilbeweises beschränkt sich auf die Aussage, dass es zu jeder natürlichen Zahl k als Zweierexponent eine natürliche Zahl n gibt, so dass 3n+1=22k erfüllt ist und der Algorithmus nach endlich vielen Schritten zum Ende kommt. Mal sehen, ob das in der Darstellung richtig herauskommt.
Mit zusätzlichen Überlegungen würde der letzte Teilschritt des Algorithmus bewiesen, dass jedes n in eine Zweierpotenz mündet, wodurch der Algorithmus zum Ende kommt. Einen vollständigen Beweis gibt es bis heute in der Tat nicht. Die Grundidee ist, dass (a+1)(a-1)=(a²-1) für jede natürliche Zahl a. In jedem Intervall [a-1,a+1] liegt genau eine natürliche Zahl 3ma für a=2k, so dass a²-1=3n oder 3n+1=a²=22k.
Offensichtlich hat die Notation mit sup in spitzen Klammern nicht funktioniert.
@ Joe Dramiga
Eventuell wäre es hilfreich – gerade für Nichtmathematiker, die wir ja alle sind – im Blogtext noch etwas ausführlicher auf die dargestellten Graphen einzugehen. Es erscheint mir so, als wäre jeweils nicht die gesamte Zahlenfolge mit allen Folgegliedern abgebildet. Das könnte damit zusammenhängen, dass das von dir verlinkte Java-Script “reduced Collatz sequences” berechnet.
@ anton reutlinger
“Die Collatz-Vermutung ist auch als Ulamfolge bekannt”
Mir nicht.
Wären Sie bitte so freundlich, hier noch einen Beleg nachzureichen oder einen nachvollziehbaren Zusammenhang zwischen beiden zu präsentieren, danke.
@Joker;
Bitte gerne, aber Sie hätten auch selber recherchieren können. Die Collatz- oder Ulamfolge ist ein beliebtes Programmierbeispiel und daher im Internet ausgiebig zu finden.
Ein zufällig ausgewähltes Beispiel: http://www.primini.de/ulam2.html
@ anton reutlinger
“Sie hätten auch selber recherchieren können.”
Hatte ich ja, bin aber schon beim ersten Treffer hängengeblieben: https://de.wikipedia.org/wiki/Ulam-Folge. Da wird sie wieder in Anspruch genommen, meine Ambiguitätstoleranz.
Bedankt hatte ich mich ja schon, aber gerne noch mal, danke.
Der Link führt auf eine Website, deren Autor behauptet die Collatz-Vermutung bewiesen zu haben. Er schreibt: “Kaum verständlich ist, daß Mathematiker meine Folgerungen /noch/ ignorieren.” Ich vermute sie haben berechtigte Gründe dafür.
Danke! Ein sehr guter und wichtiger Einwand. Da habe ich geschlampt! Ich werde oben eine Erläuterung zu den Graphen einfügen.
Jede solche Reihe kommt dann zum erwarteten Ende, wenn sie eine Zahl hervorbringt, die als x= 2^n darstellbar ist.
Jede Zahl x= 2^n lässt sich in der Form darstellen (3a+1), wenn n gerade ist. Dabei war a definiert als ungerade Zahl.
Beispiel: 2^10 = 1024 = 341×3 + 1; 2^12= 4096=1365×3 + 1 etc.
Das scheint mir ein Gesetz zu sein, denn die Differenz zwischen je zwei benachbarten Faktoren a ist stets wieder eine x=2^n, und zwar nach der Formel, dass a_n – a_(n-2) = 2^(n-2) (also im Beispiel: 1365-341= 1024 = 2^10
Mithin wären unendlich viele Zahlen vorhanden, welche eine Reihe „zum Absturz auf 1“ bringen.
Damit ist noch nichts bewiesen. Ich kann auch nichts beweisen.
Die Vermutung wäre nach meiner komplett laienhaften Vorstellung bewiesen, wenn man zeigen könnte,
dass diese Reihen sich nicht in Iterationen fangen können (andernfalls wäre sie eventuell widerlegt)
UND
dass ihre Werte für irgendeine Reihe sich nicht in auf eine Menge von Zahlen beschränkt, die keine Schnittmenge mit der Menge der Potenzen der Zahl 2 hat (also ein seltsames Muster aufweist).
Hier nehme ich bereits meinen Hut, und bin sicher, dass jeder ordentliche Mathematiker in kürzester Zeit auch solche Überlegungen anstellt.
Ich lese hier mehrfach das Wort “Reihe”. Vorsicht! Reihe und Folge sind nicht das gleiche. Eine Reihe ist eine Summenfolge, also eine spezielle Folge. Die Collatz-Vermutung beschreibt aber keine Reihe.
Reihe – Folge ….
Da sehen Sie, wie schlecht ich in Mathe bin.
@Joker;
Ja, das hatte ich auch gesehen. Ich hatte mich schon vor Jahren damit beschäftigt, deshalb ist es mir bekannt. Die wahre Urheberschaft ist anscheinand nicht eindeutig geklärt.
Hier habe ich noch eine Quelle gefunden mit einigen historischen Informationen zum Thema Collatz:
https://www.nzz.ch/article8BTQT-1.425865
Auch auf die Gefahr hin gesteinigt zu werden, welchen praktischen Nutzen haben solche Überlegungen?
Ich könnte mir eine solche Zahlenfolge für kryptische Zwecke vorstellen, was sonst?
@Bot17;
Das ist die dümmste Frage, die sich der Mensch stellen kann. Die Gewinnung von Erkenntnis und Wissen macht den Sinn des Lebens aus, oder wozu sonst hat der Mensch den Verstand? Wissen ist die Grundlage für die Bewältigung und Gestaltung des Lebens, das üben schon die Kleinkinder. Warum schauen Sie Fernsehen oder lesen eine Zeitung? Das allermeiste ist doch völlig nutzlos und zwecklos. Auch Ihr Geschreibsel hier ist nutzlos, vergeudete Zeit! Aber die Menschen sind verschieden, deshalb ist auch die Beurteilung von Nützlichkeit sehr verschieden. Und das ist gut so.
Ich kenne keinen praktischen Nutzen dieser Zahlenfolgen.
@Joe Dramiga;
Einen praktischen Nutzen kenne ich auch nicht. Ich würde aber zwischen Nutzen und Nützlichkeit unterscheiden. Eine Nützlichkeit bei der Forschung liegt auch in der Entwicklung oder Verbesserung von Werkzeugen bzw. Instrumenten, auch von Denkwerkzeugen oder mathematischen Methoden, die dann wiederum für andere Aufgaben von Nutzen sind. Ebenso kann man eventuell neue und nützliche Zusammenhänge, Strukturen, Ordnungen erkennen.
Wie aus dem historischen Überblick, den ich verlinkt hatte, zu erkennen ist, haben sich viele Mathematiker mit der Collatzfolge beschäftigt. Offenbar steckt auch Neugier und Lust dahinter, ein solches Problem zu untersuchen und eventuell zu lösen.
Anton Reutlinger,
……die dümmste Frage,
das war eine rhetorische Frage. Wenn man Grundsätzliches wissen will, etwa der praktische Nutzen der Collatz Folge, dann meine ich nicht, dass ich sie verkaufen will oder einen kommerziellen Nutzen daraus ziehen will, ich meine, bringt uns die Einsicht über diese folge auf irgendeinem Gebiet der Mathematik weiter. Ich vermute z. B . einen Zusammenhang mit den Primzahlen.
Warum kommt da nichts?
Der Mensch lebt im Schnitt etwa 750 000 Stunden. Ist da meine Frage nicht ökonomisch angebracht?
@Bote17;
Bei allen Tätigkeiten kann man nach dem Nutzen fragen. Die Frage, ob das Denken einen Nutzen hat, halte ich jedoch für sinnlos. Darauf läuft jede Frage nach dem Nutzen von Forschung letztlich hinaus. Man kann die materiellen Ressourcen für Forschung infrage stellen, aber nicht das Denken. Um solche Fragen beantworten zu können, müsste man schon vorab das Resultat der Forschung kennen, was naturgemäß nicht gegeben ist. Die allermeisten Anwendungsmöglichkeiten ergeben sich erst aus den Resultaten und oftmals erst aus dem Zusammenhang verschiedener Erkenntnisse oder Disziplinen.
Dass die Collatz-Vermutung heute eine unlösbare Knackknuss ist, sagt etwas über den Stand der Zahlentheorie aus. Dazu (der grosse) Paul Erdős: „Mathematics is not yet ready for such problems.“ und „Hopeless. Absolutely hopeless.“
Richard Guy:„Don’t try to solve these problems!“
Interessant überhaupt, dass es im Bereich der Zahlentheorie soviele ungelöste Probleme gibt. Im Abschnitt Number Theory des Open Problem Garden ist trotz mehr als 40 Einrägen, das Collatz-Problem nicht einmal aufgeführt.
Zahlentheorie als Problem, Aussagen über Eigenschaften von ganzen Zahlen zu beweisen, wird von einigen als Königsfach der Mathematik betrachtet. Interessant daran ist vor allem, dass jeder Laie einfach nachvollziehbare Vermutungen über Zahlenfolgen machen kann, dass man diese Vermutungen aber nur selten sofort bestätigen oder widerlegen kann. Mit anderen Worten: In der Zahlentheorie ist das Einfache mit dem Schwierigsten vermählt.
Martin Holzherr,
…..Zahlentheorie,
das ist die Krone der Mathematik.
Ich begreife z. B. die Primzahlen nicht. Warum fehlt denen jede Struktur ? Ich meine eine allgemeingültige Struktur, die alle Zahlen betrifft?
@ Bote17
Was wollen Sie denn da begreifen? Meinen Sie mit Struktur die Zusammensetzung der anderen Zahlen aus Primfaktoren? Da sehen Sie es doch! Ohne Ihre „strukturlosen“ Zahlen hätten Sie gar keine elementaren Bausteine für Zahlen „mit Struktur“.
Oder wie?