Wie man dem Zufall trotzt – Optimale Voraussagen
BLOG: Die Natur der Naturwissenschaft

Im letzten Beitrag habe ich stochastische Prozesse vorgestellt. An einfachsten Beispielen konnte man sehen, wie das Ergebnis der Simulation einer Gleichung eines stochastischen Prozesses aussieht: Man erhält ein Bündel von verschiedensten Lösungen, die sich alle aufgrund der Gesetzmäßigkeit, die durch die Gleichung formuliert wird, ergeben können. Es gibt also nicht nur eine Lösung, wie man es sonst von den üblichen Gleichungen her erwartet und kennt, hier sorgt der stochastische Anteil, der “Würfel” in der Gleichung dafür, dass sich bei jeder Realisierung des Prozesses eine andere Lösung ergibt. Der Zufall “pflanzt sich also fort”, die Größe x(t), die durch die Gleichung als Funktion der Zeit bestimmt werden soll, ist zu jeder Zeit nicht mehr eindeutig bestimmt, sie kann viele Werte annehmen, aber dennoch muss sich die Eigenart des “Würfels” und die der Gleichung in der Statistik der Größe x(t) zu jeder Zeit t niederschlagen.
Modellierung stochastischer Prozesse: Optimale Vorhersagbarkeit als Ziel
So wie der “Würfel”, d.h. also die Zufallsvariable, ist auch die Größe x(t) für jede Zeit t durch eine Wahrscheinlichkeitsverteilung charakterisiert, und man könnte daran denken, die Gleichung für den stochastischen Prozess nicht mit einer Simulation zu Leibe zu rücken, sondern zu versuchen, die Wahrscheinlichkeitsverteilung für x(t) zu jeder Zeit explizit auszurechnen. Das ist sehr viel schwieriger und nur für wenige Typen von Gleichungen wirklich möglich. Für Mathematiker ist das eine schöne Herausforderung, für alle anderen ist die Simulation die Methode der Wahl, und man hat eben das von der Simulation bereit gestellte Bündel von Lösungen statistisch auszuwerten, um eine endgültige Aussage über die Lösung zu treffen. Meistens begnügt man sich dabei mit den Werten für den Mittelwert und die Varianz für die Größe x(t) zu solchen Zeiten t, für die man sich im Kontext der Problemstellung interessiert. Das ist zumindest eine grobe Charakterisierung der Zufallsgröße x(t).
Eine Gleichung für einen stochastischen Prozess ist also eine Gleichung für eine zeitabhängige Zufallsvariable. Fügt man in eine beliebige, sonst übliche Gleichung für das Zeitverhalten einer Größe einen Term mit einer Zufallsvariablen ein, so “kontaminiert” dieser die ganze Gleichung, so dass die zu berechnende Größe selbst auch zu einer Zufallsvariablen wird und zu jeder Zeit verschiedenste Werte annehmen kann. Von einer eindeutigen Voraussage, wie man sie üblicherweise von einer Gleichung der Physik erwartet, kann also nun keine Rede mehr sein, man muss nun mit einem Mittelwert zufrieden sein und mit der Varianz, die ja ein Maß für die Streuung der möglichen Werte um den Mittelwert ist. Aber mehr darf man in Situationen, in denen der Zufall regiert, für eine Vorhersage nicht erwarten.
Nun ist die Qualität einer solchen Vorhersage natürlich von großem Interesse. Leider ist eine Aussage darüber nicht immer leicht zu erzielen. Ich will hier aber davon ausgehen, dass man den stochastischen Prozess, den man mathematisch mit einer Gleichung beschreiben will, in der Natur auch häufig genug beobachten kann. Dann kann man genügend aussagekräftige statistische Merkmale der Beobachtungen finden, um sie mit denen, die sich durch die Gleichung ergeben, zu vergleichen. So findet man ein Maß dafür, wie gut das mathematische Modell die Beobachtungen widerspiegelt und man kann die Frage stellen: Welches mathematische Modell passt am besten zu einem beobachteten Zufallsprozess, d.h. mit welchem Modell kann man die besten Voraussagen erwarten?
Verschiedene Typen von Gleichungen für stochastische Prozesse
Im vorherigen Beitrag habe ich Modelle vorgestellt, in denen eine beobachtbare Größe x(t) vorkommt, die nicht nur von einer externen Zufallsvariablen eta(t) sondern auch noch von den Werten von x zu früheren Zeiten t-1, t-2, …. abhängt. Man nennt solche Prozesse aus verständlichen Gründen “autoregressiv”, und offensichtlich sind solche Modelle nicht so sehr aufgrund irgendwelcher physikalischen Gesetzmäßigkeiten konzipiert worden sondern aus Gründen mathematischer Einfachheit. Irgendwie wird die Größe x zur Zeit t von ihrer Vorgeschichte abhängen, und man hofft, dass man mit dieser Unterstellung alleine schon eine gute Vorhersagefähigkeit erreicht, wenn man nur die Länge der Vorgeschichte richtig wählt und auch die Gewichte, d.h. Parameter vor den einzelnen Beiträgen x(t-1), x(t-2),… gut justiert. Dass man dabei auch noch nur diskrete Zeitschritte betrachtet, stellt eine weitere Vereinfachung dar.
Ein Physiker, der mit den Grundgleichungen der physikalischen Theorien sozialisiert worden ist, wundert sich zunächst darüber, dass man mit solch primitiven Abhängigkeiten überhaupt etwas über die Zusammenhänge bei einem beobachteten Prozess herausbekommen will. Andererseits muss er zugeben, dass man in der Physik auch mit den einfachsten linearen Gleichungen schon wichtige Gesetzmäßigkeiten beschreiben kann und dass es nicht unklug ist, bei den doch wahrscheinlich höchst komplexen beobachteten stochastischen Prozessen mit wenig Aufwand erst einmal zu testen, welchen Einfluss denn die Vorgeschichte hat.
Natürlich gibt es viele andere Modelltypen. Man kann in bekannte Differentialgleichungen der deterministischen Physik an geeigneter Stelle externe Zufallsvariablen einsetzen, um einen äußeren stochastischen Einfluss zu berücksichtigen. Dann erhält man eine stochastische Differentialgleichung; aber nur die einfachsten von diesen kann man auf dem Papier lösen, bei allen anderen muss man zu numerischen Methoden greifen und diese sind sehr aufwändig. Ein anderer, auch sehr wichtiger Modelltyp wird durch eine so genannte Master-Gleichung repräsentiert. Diese beschreibt einen so genannten Markov-Prozess, der im wesentlichen durch die Wahrscheinlichkeit bestimmt ist, dass bei gegebenem Wert x0 zur Zeit t die Größe x zum Zeitpunkt t+1 den Wert x1 besitzt. Die Größe x springt also dabei zu bestimmten Zeiten mit einer bestimmten Wahrscheinlichkeit auf einen anderen Wert. Eine typische Trajektorie ist in Abb. 1 dargestellt.
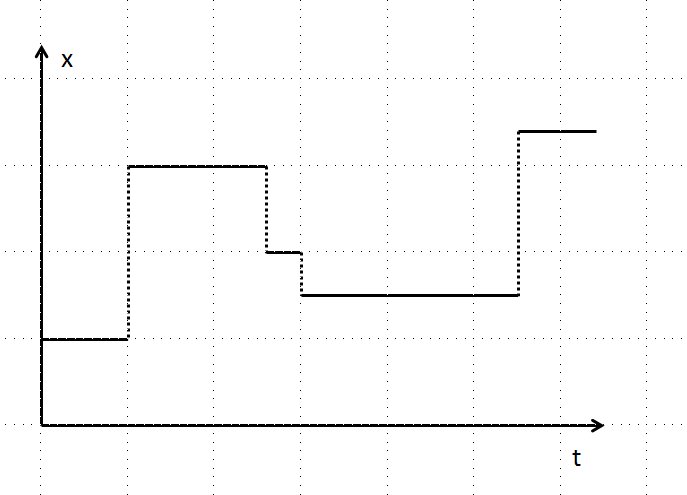
Abb1. Typischer Verlauf eines Markov-Prozesses: Zu zufälligen Zeiten springt x(t) in einen anderen, sich zufällig ergebenden Zustand
Auch sind noch die so genannten verborgenen Prozesse zu erwähnen, in denen in Rechnung gestellt wird, dass man manche Prozesse nicht direkt beobachtet; neben den Gleichungen für den Prozess selbst muss man noch eine Gleichung für den Beobachtungsprozess formulieren.
Schätzung der Parameter eines Modells
Dieser Exkurs über verschiedenste Typen von mathematischen Modellen für stochastische Prozesse soll nur zeigen, dass man in der Analyse stochastischer Prozesse nicht nur auf die simplen autoregressiven Modelle setzt. An diesen kann man aber sehr übersichtlich die wichtigen Fragen diskutieren, die sich bei der Modellierung stochastischer Prozesse ergeben:
In der deterministischen Physik kann man für die Analyse eines Prozesses stets auf Gesetzmäßigkeiten zurückgreifen, die sich aus den Grundgleichungen des entsprechenden Gebietes der Physik ergeben. Hier nun, bei dem Versuch, ein mathematisches Modell für einen stochastischen Prozess zu finden, muss man sich zunächst einmal für einen bestimmten Modelltyp entscheiden, der nur einem “sehr weiten Mantel” gleicht. Wäre dieser Typ ein autoregressives Modell der Form x(t) = a1 x(t-1) + … + ap x(t-p) + eta(t), so hat man also noch die Parameter p und a1 , …, ap zu bestimmen, wobei p angibt, wie weit man die Vorgeschichte berücksichtigen will, und wobei a1 , …, ap die Gewichte der Werte von x zu früheren Zeiten darstellen. Man hat also durch die Wahl von p das Modell noch weiter zu spezifizieren, und dann bei gegebenem Modell die Parameter des Modells selbst zu bestimmen. Dieses alles muss natürlich dazu führen, dass das “fertige” Modell genau das ist, dass für den in Frage stehenden stochastischen Prozess die größte Vorhersagekraft besitzt. Es liefert dann den “besten linearen Prädiktor”. Solche optimierten, auf einem linearen stochastischen Modell basierenden “Vorhersager” spielen eine große Rolle z.B. in Ökonometrie, Neurologie oder Klanganalyse. Natürlich kann dabei auf gleiche Weise berücksichtigt werden, dass x(t) auch von anderen Größen zu gleichen oder früheren Zeiten beeinflusst wird.
Naturgesetze vs. optimierte Prädiktoren
Ich will hier nicht darauf eingehen, wie man mit Kriterien der mathematischen Statistik die das “richtige” Modell und darin die “richtigen” Parameter bestimmt. Wichtiger ist hier die Beobachtung, dass man in diesem Rahmen gar nicht über Naturgesetze redet, sondern dass es hier nur um Vorhersagefähigkeit geht. Nun dienen Naturgesetze in der Praxis letztlich ja auch immer nur der Vorhersage, und so erscheint hier die Vorhersagefähigkeit das allgemeinere Ziel der Naturforschung überhaupt zu sein.
Aber das ist ja nur ein sehr pragmatischer Zugang; andererseits stehen die Naturgesetze ja nicht isoliert und unabhängig voneinander da sondern sind eingebunden in eine Hierarchie von Aussagen, an deren Spitze bestimmte Grundaussagen stehen, aus denen dann alle anderen Aussagen über Regelmäßigkeiten in einen bestimmten Phänomenbereich folgen. Diese gesamte Hierarchie bildet die gesamte physikalische Theorie. Auf eine solche Einbettung in einen größeren Zusammenhang verzichtet man also, wenn man Modelle wie die oben angeführten für stochastische Prozesse entwickelt. Man tut es notgedrungen, weil eine Modellierung auf der Basis präziser physikalischer oder anderer naturwissenschaftlicher Gesetze zu aufwändig wäre oder höchstens zu Gleichungen führte, die zu viele unbekannte Parameter enthielte. Man nennt in der Physik solche Modelle, die nur darauf abzielen, das Phänomen quantitativ zu beschreiben, auch phänomenologische Modelle. Der Prototyp eines solchen Modells stellen die Keplerschen Gesetze dar. Hier werden auch nur die Bahnen der Planeten mathematisch beschrieben, eine Rückführung auf ein grundsätzlicheres Gesetz gelang erst Isaac Newton, und diese Überlegungen führten ihn sogar zum Aufbau einer Theorie der Bewegung, die zum Vorbild für alle Wissenschaft wurde und den Zeitgenossen auch schon als der Höhepunkt aller Wissenschaft erschien. Auf dieser Ebene der Komplexität, als es noch “nur” um Planetenbahnen ging, musste man sich also auf die Dauer nicht mit phänomenologischen Gesetzen begnügen. Hier war das Maß der Komplexität noch gering genug und die Beobachtungen so präzise, dass die Regelmäßigkeiten zur Formulierung deterministischer Gesetzmäßigkeiten führten.
In unserer Alltagswelt scheinen die höchst regelmäßigen Prozesse einen Idealfall darzustellen. Mediziner, Ökonomen und Psychologen reden von Wahrscheinlichkeiten, (wenn sie nicht den Mund zu voll nehmen); bei ihnen gilt die Regel “Keine Regel ohne Ausnahme”, (wobei die Ausnahme von dieser Regel die deterministische Physik darstellt). Man darf nicht erwarten, dass sich hier die “heile Welt” der deterministischen Physik einstellt, wenn man nur genügend forscht. Systeme können nun einmal so komplex werden, dass man sie nur dann quantitativ beschreiben kann, wenn man akzeptiert, dass man mit einem Mangel an Wissen zu rechnen (in beiderlei Bedeutung) hat. So werden wir es immer mit Unsicherheiten zu tun haben, wir können aber dafür arbeiten, dass wir sie so klein wie möglich halten und dass wir mit den verbleibenden Risiken so rational wie möglich umgehen lernen.


“Man darf nicht erwarten, dass sich hier(Medizin,Ökonomie,Psychologie,jmg) die “heile Welt” der deterministischen Physik einstellt, wenn man nur genügend forscht.”
Dieser Satz hat mich an folgendes erinnert:
Christopher Sims, der diesjährige Nobelpreisträger für Ökonomie (zusammen mit Tom Sargent), erläutert in seiner Nobel Prize lecture, wie wissenschaftlicher Fortschritt in seinem Fach aussieht.
VIDEO_LINK:http://www.nobelprize.org/…yer/index.php?id=1743 (ca. 34 Minuten)
Sims:”Real scientific progress in economics is not as pretty as real scientific progress in the natural sciences. It’s a little messy and I hope I give you a sense of that.”
Jan Tinbergen, dessen Arbeiten von Sims ganz zu Beginn besprochen werden, war ein Schüler des Physikers Paul Ehrenfest. Sims selbst ist Anhänger der Bayesianischen Statistik (auf die er ab 14:45 Min eingeht), die mit Methoden (Markov Chain Monte Carlo), die zuerst von Physikern entwickelt wurden, versucht ökonometrische Modelle zu schätzen. Sims hat
vektorautoregressive Modelle (eine einfache Verallgemeinerung des von ihnen erwähnten autoregressiven Prozesses) in der Ökonometrie populär gemacht. Bekannt geworden ist er durch seine Arbeiten in den frühen 70-er Jahren zur “Kausalität” in statistischen Beziehungen.
Interessant ist auch das Interview mit Sims und Sargent(so ab Minute 10:00), in dem sie auch auf den Unterschied zwischen Experimenten in ökonomischen Modellen und Experimenten in den Naturwissenschaften eingehen.
VIDEO-LINK: http://www.nobelprize.org/…yer/index.php?id=1747
Komplexitätsgrenzen
Bei Real-Systemen welcher Komplexität winkt der Stochastiker mangels Erfolgsaussichten i.p. “Wissenserkennung” ab? Kann man diese sinnvoll kategorisieren?
MFG
Dr. Webbaer
@jmg
Vielen Dank für die Zitate, werde mir sie aber erst im Neuen Jahr anschauen können.
Dr. Webbaer
“Bei Real-Systemen welcher Komplexität winkt der Stochastiker mangels Erfolgsaussichten i.p. “Wissenserkennung” ab? Kann man diese sinnvoll kategorisieren?”
Da kann man keine Regel aufstellen und sich auch wohl keine vorstellen. Dazu gibt es zu viele verschiedene Arten von komplexen Systemen und von Menschen.
@jmg
Die Ökonomen haben wie viele Physiker auch wohl erst spät gelernt, mit Zufallsprozessen umzugehen. Sims redet auch lieber noch von Wahrscheinlichkeitsverteilungen statt von Zufallsvariablen.
Noch mehr fällt mir aber immer auf, dass in der Ökonomie zwar Methoden aus der Statistik bzw. Statistischen Physik wie Markov Chain Monte Carlo und vektorautoregressive Modelle importiert und angewandt werden, eine Diskussion über Annahmen und deren Begründung aber einem vergleichsweise niedrigem Niveau stattfindet. Die mathematischen Methoden, das Handwerkliche kennt man auch als Physiker; man möchte aber mehr über Arbeit an Begriffen und Annahmen erfahren, so etwas wie eine Philosophie des ökonomischen Handelns sehen. Diskussionen über persönliche Erfahrungen reichen da nicht aus.
Auswirkungen auf Finanzmärkte
Ich vermute, die Auswirkungen der Modellierung auf den Finanzmarkt bzw. die realen Möglichkeiten “Geld” an “der Börse” zu verdienen, sind beträchtlich.
Hier ist m.E. nicht nur eine Philosophie der Ökonomie gefragt, sondern auch eine ethische Diskussion, wie mit den Vorhersagen und auch den Vorhersagemöglichkeiten generell umgegangen werden sollte.
NeuroBayes
Zur Ökonomie noch der Hinweis, dass Prof. Feindt vom KIT die Software NeuroBayes vermarktet. Dabei werden anscheinend die Algorithmen aus der Teilchenphysik auch auf wirtschaftliche Fragestellungen angewendet. Wesentlich scheint das Trainieren neuronaler Netze zu sein.
http://arxiv.org/abs/physics/0402093