Nach der Einführung in die Aussagenlogik in den letzten beiden Blogbeiträgen müsste ich hier ein wenig innehalten, um auf wichtige Stationen in der Geschichte der Logik zurückzublicken. Schließlich liegen zwischen der Zeit des Aristoteles und der von Frege und Russell immerhin mehr als 2.000 Jahre, in der man die Aristotelische Logik hin und her gewendet hat und man mitunter auch nach „Besserem“ suchte.  Die Idee, eine Logik für Aussagen zu entwerfen und dann noch im Rahmen einer formalen Sprache, fiel ja nicht vom Himmel.

Es ist aber nicht möglich, hier auch nur einen halbwegs repräsentativen Überblick über all die Werke zu geben, die im Laufe der 2.000 Jahre über logische Probleme geschrieben worden sind. Ich könnte nur mit großen Schritten durch die Geschichte springen und hier und da einen wichtigen Gedanken aufsammeln. Insgesamt wäre das unbefriedigend. Ich kann hier nur auf die drei Bände von Franz Schupp: Geschichte der Philosophie im Überblick verweisen (Schupp, 2003). Der Autor hat die Bedeutung der Logik für die Geistesgeschichte erkannt und legt deshalb ein besonderes Augenmerk auf die Entwicklung der Logik.

Auf jeden Fall muss ich aber hier noch einige wichtige Erweiterungen der Aussagenlogik erwähnen, um den Leser nicht im Glauben zu lassen, er oder sie hätten mit der Aussagenlogik schon einen großen Teil der Logik kennengelernt. Die Ausdrucksmöglichkeit der Aussagenlogik ist ja noch sehr beschränkt und eine Erweiterung in diese oder jene Richtung wird man sich bald wünschen, wenn man sich länger damit beschäftigt. Das Wissen, das ich bisher über die Herkunft und Bedeutung der Schlussregeln bereitgestellt habe, genügt aber, um die weiteren Überlegungen in diesem Blog zur Geschichte des Logos zu verstehen.

Prädikatenlogik

Mit der Aussagenlogik kann man Schlussregeln finden, die von wahren Aussagen notwendig zu wahren Aussagen führen. Der Modus ponens ist hier der Prototyp einer solchen Schlussregel.  Wir kennen aber aus der Aristotelischen Logik noch andere Schlüsse, die vom Wahren wieder notwendig zum Wahren führen, z.B. die beiden Sätze „Alle Menschen sind sterblich“ und „Sokrates ist ein Mensch“. führen zu „Sokrates ist sterblich“.  

Hier tritt in dem Einzelsatz „Alle Menschen sind sterblich“ das Wort „Alle“ auf.  Man könnte weiterhin den Satz als Ganzes und dessen Wahrheitswert betrachten und damit bei der Aussagenlogik bleiben. Man kann aber auch ins „Innere“ des Satzes schauen und bemerken, dass hier die Anzahl von Elementen einer Menge ins Spiel kommt. Das ist nicht immer so, aber im Hinblick auf das Ziel, sich möglichst detailliert auszudrücken, sollte man diesen Unterschied in einer formalen Sprache auch berücksichtigen. Das hat zu der Erweiterung der Aussagenlogik zur so genannten Prädikatenlogik geführt, in der man nun für die Aussagen eine besondere Struktur vorsieht, nämlich eine Quantifizierung mit „Quantoren“ wie „Alle“ oder „Keine“.

Entscheidend für eine solche Erweiterung wurde dabei, dass man lernte, dem Begriff „Prädikat“, den wir ja aus der Grammatik einer natürlichen Sprache kennen, eine allgemeinere Bedeutung beizugeben. Unter einem Prädikat versteht man in der Logik alles, was man einem Objekt sinnvollerweise zusprechen, eben „prädizieren“ kann. In dem Satz „Sokrates denkt“ ist also „denkt“ das Prädikat. Neben Eigenschaften können das z.B. also auch Verben sein. Aber auch mehrstellige Relationen, z.B.  R(x,y) können Prädikate sein; hier wird nun zwei Objekten x und y eine Relation zugesprochen.

Als beste Übersetzung solcher Sätze in Zeichenketten hat sich erwiesen, dass man z.B. ein einstelliges Prädikat als Funktion einer Variablen sieht und das Objekt, dem das Prädikat zugeordnet wird, als Argument. Die Funktion s(x) bedeutet dann, dass dem Objekt „x“ das Prädikat s≔ „ist sterblich“ prädiziert, also zugesprochen wird. Man kann dann leicht formulieren, dass das Prädikat mehreren oder allen Objekten aus einer vorgegebenen Menge zukommt oder auch keinem. Dadurch ergibt sich also die Möglichkeit der Quantifizierung.

Diese Funktion s(…) hat als Funktionswert den Wahrheitswert dieser Aussage; s(x) ist also 1 bzw. wahr, wenn x sterblich ist. Wenn wir nun noch die Funktion M(x) definieren mit M(…):= „ist ein Mensch“, können wir nun formulieren:

Für alle x gilt:  Wenn x ein Mensch ist, dann ist x sterblich, oder

∀x (M(x) → s(x)).

wobei wir das Symbol ∀x für „Für alle x“ eingeführt haben.  Man nennt das Symbol „∀“ einen Quantor. Man muss natürlich vorher festlegen, auf welche Menge sich denn „alle“ bezieht. Nützlich ist noch das Symbol „∃x“ für „Es gibt ein x“. Im Prinzip kann man aber allein mit dem Symbol „∀“ für alle Quantifizierungen auskommen.

Die Prädikatenlogik umfasst also die Aussagenlogik. Schlussregeln in der Prädikatenlogik sind zunächst:

M(x) ∧ (x = a) ⊨ M(a),

d.h. „Kommt ein Prädikat allen x aus einer vorgegebenen Menge zu, dann auch einem einzelnen Element a dieser Menge“, und

M(a) ⊨ ∃x M(x),

d.h. Kommt einem Objekt a die Eigenschaft M zu, so gibt es ein Objekt x, dem die Eigenschaft M zukommt.

Schließlich geht es nicht ohne den Modus ponens, z.B. in der Form

M(S), ∀x (M(x) → s(x)) ⊨ s(S),

wobei „S“ für ein spezielles Element x aus der vorgegebenen Menge steht.

In der Prädikatenlogik lassen sich auch alle Syllogismen der Aristotelischen Begriffslogik formulieren. Der Syllogismus Barbara lautet hier z.B.:

∀x (G(x) → M(x)), ∀x (M(x) → s(x)) ⊨ ∀x (G(x) → s(x))

wobei “G” für “ist Grieche” stehe. Hier wird ein Schluss angewendet, den man aus dem Modus ponens ableiten kann. Die hier verwendete Schlussregel

(A → B), (B→ C) ⊨ (A → C)

ist aber auch direkt aus der Tautologie

((A → B) ∧ (B → C)) → (A → C)

ableitbar.

Bisher hat sich das Quantifizieren immer auf das Objekt x, einem Element aus einer vorgegebenen Menge, erstreckt. Man spricht hier von einer Prädikatenlogik 1. Stufe. Man kann nämlich auch eine Prädikatenlogik 2. Stufe einführen, indem man die Quantifizierung auch auf die Prädikate erstreckt.

Wir wollen das an einem berühmten Beispiel studieren: Betrachten wir zunächst die Aussage

P(x) → P(S(x)),

d.h. Wenn das Prädikat dem Objekt x zukommt, dann auch dem Objekt S(x). Das ergibt z.B. einen Sinn, wenn x eine Zahl ist und S(x) = x + 1 ist, also der Nachfolger von x. Wenn z.B. eine Gleichung für x erfüllt ist, dann ist sie auch für x + 1 erfüllt.

Dieses kann man für alle natürlichen Zahlen fordern, und erhält

∀x (P(x) → P(S(x))).

Das ist eine der Voraussetzungen für ein besonders prominentes Schlussverfahren in der Zahlentheorie, die „vollständige Induktion“. Man darf hier das Wort „Induktion“ nicht mit der logischen Induktion verwechseln. Die Gefahr, es mit der physikalischen Induktion zu verwechseln ist wohl geringer. Um zu einer Konklusion zu gelangen, muss es noch einen Induktionsbeginn geben, z.B. P(0), d.h. die Eigenschaft P kommt der Zahl 0 zu. Dann nämlich folgt ∀x P(x), d.h. die Eigenschaft P kommt allen natürlichen Zahlen x zu.

Will man nun diese Aussage ∀x (P(x) → P(S(x))) für alle Prädikate P fordern, so schreibt man also:

∀P [∀x (P(x) → P(S(x)))].

Das ist also eine Aussage in der Sprache der Prädikatenlogik 2. Stufe.

Man kann auch das Prädizieren, also das Zusprechen einer Eigenschaft insofern weitertreiben, indem man Eigenschaften, also Prädikaten, wiederum Eigenschaften zuspricht. Bezeichne F eine Eigenschaft, die einer Eigenschaften P zugesprochen werden kann, so kann man z.B. zunächst formulieren:

F(P) → P(x),

also: Wenn einer Eigenschaft P die Eigenschaft F zukommt, dann besitzt auch   x auch diese Eigenschaft. Wenn man das für alle Eigenschaften P einer bestimmten Menge von Eigenschaften fordert, kann man z.B. formulieren:

∃x ∀P(F(P) → P(x))

d.h. Für alle Eigenschaften P gilt: Haben sie die Eigenschaft F, so gibt es auch ein Objekt x, dass alle diese Eigenschaften P hat.

Bedeute die Eigenschaft F „ist gut“, was immer das auch sei, dann sagt der Satz: „Es gibt ein Objekt, dass alle guten Eigenschaften besitzt.“ Damit ist natürlich nichts darüber gesagt, ob dieser Ausdruck wahr ist oder aus irgendwelchen Axiomen abgeleitet werden kann. Man kann ihn nur formulieren.

Über die Unterschiede der beiden Prädikatenlogiken gibt es in der mathematischen Logik tiefliegende Sätze, zu denen man nur durch ein intensives Studium Zugang erlangen kann. Hier kann nur gezeigt werden, wie man die Sprache der Aussagenlogik erweitern kann. Festzuhalten bleibt, dass die Schlussregeln der Prädikatenlogik 1. Stufe „als Bausteine für alle mathematischen Argumentationsweisen ausreichen“ (Ebbinghaus & Thomas, 2018, p. 62). 

Die modale und deontische Logik

In der Aussagen- und Prädikatenlogik beschränkt man sich immer nur einen bestimmten Typ von Aussagen, nämlich auf solche, die entweder wahr oder falsch sein können. Es gilt hier ja der Satz vom Ausgeschlossenen Dritten, A ∨ ¬A ist eine Tautologie. 

Oft aber wissen wir nicht, ob die Aussage A über eine Tatsache wirklich wahr ist. Wenn wir nun im Folgenden kleine Buchstaben p, q, … für Aussagen einführen, damit die Notation später übersichtlich bleibt, wollen wir also auch in Betracht ziehen, dass es nur möglich ist, dass eine Aussage p wahr ist. Bei Aussagen p, die wir nach logisch korrekten Schlussregeln aus akzeptierten Annahmen abgeleitet haben, würden wir dann aber sagen, dass die Aussage p notwendig wahr ist.

Schließlich kennen wir auch die Situation, in der wir über eine Tatsache nur sagen können, dass sie möglich sein kann aber nicht notwendig sein muss, dass sie also „kontingent“ ist. Erweitert man die Sprache der Prädikatenlogik 1. Stufe um Zeichen für solche Begriffe, spricht man von einer Modallogik.

Ganz analog kann eine andere Erweiterung der Sprache der Aussagenlogik entwickelt werden, in der es um Pflichten wie Gebote oder Verbote geht. Man erhält dann eine deontische Logik (δέον, δέῖ gr. = man muss). Gebieten kann man aber keine Aussagen, aber Handlungen: Das Symbol „p“ stehe dann also für eine Handlung statt für eine Aussage. Handlungen kann man aber auch verbieten oder auch weder verbieten noch gebieten, also nur erlauben.

Wir sehen hier Parallelen zwischen den Begriffen „notwendig, unmöglich, kontingent“ und „geboten, verboten, erlaubt“. In Abb. 1 werden diese auch deutlich.

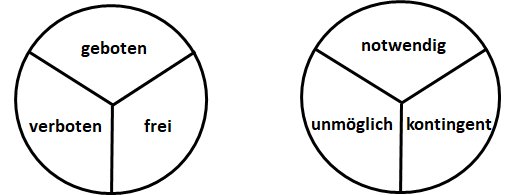
Es zeigt sich, dass die modalen Begriffe „notwendig“, „unmöglich“ und kontingent“ zu den jeweils anderen beiden Begriffen disjunkt sind: Was nicht notwendig ist, kann unmöglich sein, aber auch kontingent. Was nicht unmöglich ist, kann kontingent, aber sogar notwendig sein, und was nicht kontingent ist, ist entweder notwendig oder unmöglich. Entsprechendes gilt für die deontischen Begriffe: Was nicht geboten ist, kann verboten sein, aber auch erlaubt, usw.

Mit diesen drei Begriffen muss man nun jeweils die formale Sprache der Aussagenlogik erweitern, indem man neue Symbole einführt. Eigentlich braucht man jeweils nur für einen Begriff ein Symbol, denn es zeigt sich, dass man alle anderen dann mit Hilfe von Negationen durch dieses eine Symbol ausdrücken kann.

Dieses neue Symbol soll in der modalen Logik das Zeichen „N“ sein, welches auch als ein Operator aufgefasst werden kann, der auf eine Aussage p wirkt: „Np“ soll dann bedeuten: „Es ist notwendig, dass p wahr ist.“

In der modalen Logik führen wir den Operator „G“ ein, „Gp“ bedeute nun: „Es ist geboten, dass die Handlung p ausgeführt wird“.  

Insgesamt erhält man so:

Np:  Es ist notwendig, dass p wahr ist, d.h. es ist unmöglich, dass p falsch ist,

¬Np:  Es ist nicht notwendig, dass p wahr ist, d.h. es ist nicht unmöglich, dass p falsch ist,

 N¬p: Es ist notwendig, dass p falsch ist, d.h. es ist unmöglich, dass p wahr ist,

¬N¬p: Es ist nicht notwendig, dass p falsch ist, d.h. es ist nicht unmöglich, dass p wahr ist,

¬Np ∧ ¬N¬p: Die Aussage p ist kontingenterweise wahr, da sie nicht notwendig und nicht unmöglich wahr ist.

Entsprechend kann man formulieren:

Gp: Es ist geboten, die Handlung p auszuführen,

¬Gp: Es ist nicht geboten, die Handlung p auszuführen,

G¬p: Es ist geboten, die Handlung p nicht auszuführen, d.h. es ist verboten, die Handlung p auszuführen,

¬G¬p: Es ist nicht verboten, die Handlung p nicht auszuführen. Es ist also erlaubt, die Handlung p auszuführen.

¬Gp ∧ ¬G¬p: Es ist weder geboten noch verboten, p auszuführen (nichtpflichtiger Fall).

Man muss hier unterscheiden zwischen Normen, die mit dem Satz gesetzt werden sollen, und Normsätzen, d.h. Aussagen über Normen. Erstere werden durch Setzung in Gültigkeit gebracht, die Aussagen über Normen können wahr oder falsch sein können.

Damit sind auch hier die neuen Zeichen und ihre Bedeutung eingeführt. In Abb. 2 sind diese in dem so genannten modalen bzw. deontischen Sechseck übersichtlich dargestellt.

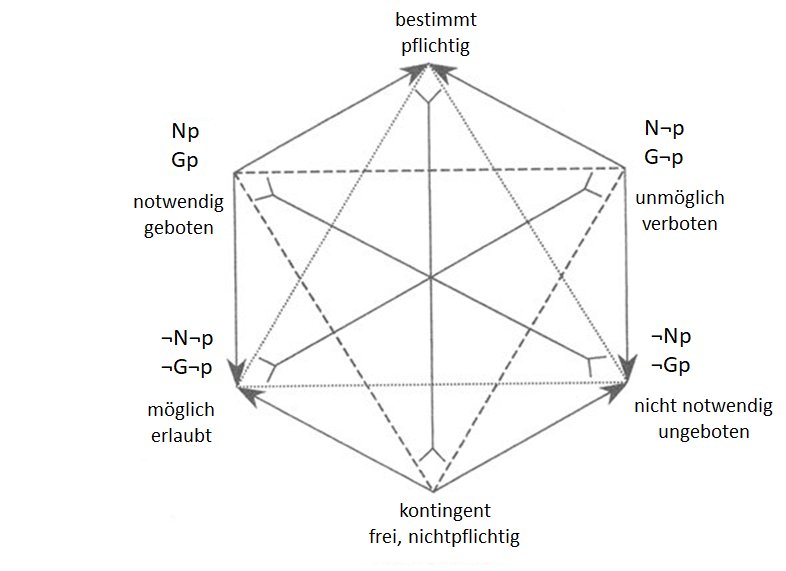
Weitere Ausführungen wie die Diskussion möglicher Axiome und eines Kalküls im Zusammenhang mit dem Kalkül der Aussagenlogik gehen über den Rahmen dieses Blogs hinaus.

Ausblick

Hiermit ist die Liste der Erweiterungen der Aussagenlogik aber noch in keiner Weise abgearbeitet. Es gibt auch so genannte nichtklassische Logiken, in denen z.B. der Satz vom Ausgeschlossenen Dritten nicht gilt. Man geht dann nicht davon aus, dass Aussagen nur entweder wahr oder falsch sind. In der modalen Logik haben wir das noch unterstellt, nur die Möglichkeit berücksichtigt, dass man es nicht genau weiß. Hier nun soll darauf verzichtet werden, dass es „ontologisch“ nur diese Alternative gibt. Der Boolesche Verband der Aussagen wird nun nicht mehr auf einen zweiwertigen Boolesche Verband, sondern auf eine andere Struktur abzubilden sein. Eine Fülle von Ansätzen solcher mehrwertigen Logiken gibt es, die intuitionistische Logik ist ein prominentes Beispiel dafür.

Hier muss auch die so genannte Fuzzy-Logik erwähnt werden. Sie lässt noch Nuancierungen der Prädikate wie „sehr“ oder „ziemlich“ zu, fasst diese aber wieder quantitativ. Bei vielen Anwendungen in der Regelungstechnik spielt sie eine bedeutende Rolle.

Am besten ausgearbeitet aber ist der „Umgang mit unsicherem Wissen“, welcher sich auf die mathematische Wahrscheinlichkeitstheorie stützt. Hier wird einer Aussage ein Maß für die Wahrscheinlichkeit dafür zugeordnet, dass sie wahr ist. Dieses kann man auch als Maß für die Glaubwürdigkeit einer Aussage betrachten. Damit können wir das Thema von Aristoteles aufgreifen, welches er bei der Klassifikation der Schlüsse anklingen ließ, als der von einem dialektischen Schluss sprach. Hier stellten sich schon Fragen ein, die man damals unmöglich beantworten konnte: Was kann man über eine Konklusion in dialektischen Schlüssen sagen? Kann man sogar einen Kalkül auch für Aussagen entwickeln, welche lediglich glaubwürdig sind? Wie könnte man in einem solchen Kalkül so streng wie möglich Schlussfolgerungen ziehen? Was würde denn hier überhaupt „streng“ bedeuten? In den nächsten Blogbeiträgen will ich mich diesen Fragen widmen.