Nachdem ich im letzten Blogbeitrag eine mathematische Struktur und deren Interpretation für einen Umgang mit unsicherem Wissen vorgestellt habe, können wir nun die ersten Folgerungen daraus ziehen. Wir werden dabei sehen, wie man einen dialektischen Schluss präzise fassen kann und lernen, was bei unsicherem Wissen im Hinblick auf Schlussfolgerungen noch möglich ist. Das Bayessche Theorem, auf das wir dabei stoßen, wurde lange Zeit verkannt, hat sich inzwischen aber als ungemein nützlich in jedwedem Umgang mit unsicherem Wissen erwiesen.

Die Entwicklungsregel

Das, was beim unsicheren Wissen von einer logischen Schlussfolgerung übrigbleibt, kann man am besten an der so genannten Entwicklungsregel verdeutlichen. Diese tritt nämlich an die Stelle des Modus ponens.

Wir erinnern uns an diesen hier in der Form H ∧ (H → D) ⊨ D. Es seien also D und H zwei mögliche Aussagen bzw. Ereignisse; dabei soll nun „H“ für eine Hypothese stehen, „D“ für Daten, also für einen empirischen Befund.

Dann lässt sich aus den Axiomen ableiten:

P(D) = P(D|H) ∙ P(H) + P(D|¬H) ∙ P(¬H).

Der Beweis ist ein Zweizeiler:  Wir betrachten, mit ⊤ = H ∨ ¬H:  

P(D) = P(D ∧ ⊤) =  P(D ∧ (H ∨ ¬H)) = P((D ∧ H) ∨ (D ∧ ¬H)) =

P(D ∧ H) + P(D ∧ ¬H) = P(D|H)∙P(H) + P(D|¬H)∙P(¬H).

Der erste Term P(D|H)∙P(H) auf der rechten Seite der Gleichung für P(D) erinnert an den Modus ponens: Statt der Aussage H steht nun P(H), statt der Implikation steht nun die Glaubwürdigkeit von D bei gegebenem H, und statt mit einer Verknüpfung „∧“ der Aussagen haben wir es hier nun mit einer Multiplikation, also einer Verknüpfung im Raum der reellen Zahlen zu tun. Wir befinden uns zwar in einer ganz anderen mathematischen Struktur, aber die Protagonisten D und H spielen entsprechende Rollen.

Entscheidend ist aber, dass es da noch einen zweiten Term gibt, in dem auch die Negation ¬H der Hypothese auftritt. Das ist nun aber plausibel: Man muss ja jetzt auch in Rechnung stellen, dass ¬H wahr ist, insofern muss auch P(D|¬H) irgendwie berücksichtigt werden, also, wie glaubwürdig die Daten D bei einer falschen Hypothese wären.

Das Bayessche Theorem

Neben einem „Rest einer Schlussfolgerung“ entdeckt man aber bei unsicherem Wissen eine ganz andere Art von Schlussfolgerung, die es beim sicheren Wissen gar nicht gibt. Hier geht es nämlich um Glaubwürdigkeitsgrade, und zwar um eine Revision bei der Zuordnung von Glaubwürdigkeitsgraden aufgrund neuer Information.

Wir betrachten dazu wieder zwei Ereignisse/Aussagen H und D. Mit Hilfe der Relationen

P(H ∧ D) = P(D|H)∙P(H) und

P(H ∧ D)  = P(D ∧ H) = P(H|D) ∙ P(D).

erhält man nun sofort

P(H|D) ∙ P(D) = P(D|H) ∙ P(H)

und somit

P(H|D) = P(D|H) ∙ P(H) / P(D).

Mit dem Ergebnis der Entwicklungsregel,

P(D) = P(D|H) ∙ P(H) + P(D|¬H) ∙ P(¬H),

kann man diese Aussage auch schreiben als

P(H|D) = P(D|H) ∙ P(H) / (P(D|H) ∙ P(H) + P(D|¬H) ∙ P(¬H)).

Dies ist das Bayessche Theorem. So trivial die Herleitung auch ist, die Bedeutung und Nützlichkeit dieser Relation ist nicht zu überschätzen.

Ist P(H) = 0: Dann ist auch P(H|D) = 0. Wenn H mit Sicherheit nicht eintritt, dann ändert ein Ereignis D auch nichts daran.

Ist P(D|H) = 0, ist auch P(H|D) = 0. Ist unter der Hypothese H die Wahrscheinlichkeit für den Datenbefund gleich 0, so ist auch eine Glaubwürdigkeit der Hypothese bei vorliegendem Datenbefund D nicht berechtigt.

Seien nun P(H) und P(D|H) größer als 0. Mit P(¬H) = 1 – P(H) können wir die Formel auch wie folgt schreiben:

P(H|D) = f₁ ∙ P(H),

mit dem Verstärkungsfaktor f₁, dessen Kehrwert wir hier der Übersichtlichkeit halber angeben:

1/f₁ = P(H) + (1 – P(H)) ∙ P(D|¬H) /P(D|H).

Das Bayessche Theorem beschreibt also, wie sich der Glaubwürdigkeitsgrad von H unter Berücksichtigung von Daten D verändert. Man revidiert aufgrund von Daten, also zusätzlichem Wissen, die a-priori Glaubwürdigkeit. Man sieht sofort, dass man eine solche Revision immer aufs Neue machen kann, wenn neue Daten, neue Erfahrungen vorliegen. Angesichts der Tatsache, dass es hier um einen Umgang mit unsicherem Wissen geht, erscheint solch eine Möglichkeit, wenigstens neue Information stets auf einer logisch strengen Weise verwerten zu können, optimal.

Eine andere Version des Bayesschen Theorems ergibt sich übrigens, wenn man sich anschaut, wie die „Chance“ (engl. odds) ≔ P(H)/P(¬H) durch Kenntnisnahme von Daten revidiert wird. Indem man das Verhältnis der Gleichungen P(H|D)∙P(D) = P(D|H)∙P(H) und P(¬H|D)∙P(D) = P(D|¬H)∙P(¬H) bildet, erhält man

P(H|D) / P(¬H|D) = f₂ ∙ P(H)/P(¬H), mit

f₂ = P(D|H) / P(D|¬H).

Der Verstärkungsfaktor für die jeweilige Chance ist also übersichtlicher.

Der englischen presbyterianische Pfarrer und Mathematiker Thomas Bayes hat diese Strategie für eine iterative Verbesserung einer Vermutung auf der Basis neuer Information entdeckt und auch aufgeschrieben. Die Schriften dazu sind aber erst nach seinem Tod im Jahre 1761 von seinem Freund Richard Price gefunden und herausgegeben worden. Der französische Mathematiker und Physiker Pierre-Simon Laplace (1749 bis 1827) soll das Theorem im Jahre 1774 ebenso entdeckt und dann in die heutige Form gebracht haben. Lange Zeit galt das Theorem als unwissenschaftlich, weil es subjektive Einschätzungen berücksichtigte. Dabei beschreibt diese Strategie eigentlich auch die grundsätzliche Entwicklung physikalischer Theorie sehr genau:  Aufgrund neuer Information, neuer Daten findet man das „Bessere“, hier eben eine bessere Glaubwürdigkeit.

Im Zweiten Weltkrieg konnten einige Forscher spektakuläre Erfolge mit dieser Methode verzeichnen. Heute ist sie aus Anwendungen vieler Gebiete, in denen es um einen Umgang mit unsicherem Wissen geht, nicht mehr wegzudenken (Für die Geschichte des Theorems siehe z.B. (McGrayne, 2014)).

Bevor wir dieses Theorem an einigen Beispielen demonstrieren, prüfen wir erst einmal, ob die Formel in Spezialfällen auch das Erwartete liefert:

• Sei P(H) = 1:  Dann folgt P(H|D) = 1. Wenn H mit Sicherheit eintritt, dann ändert die Berücksichtigung Daten D nichts daran.
• Sei P(D|H) = P(D), d.h. D wird durch H nicht beeinflusst. Aus dem Bayesschen Theorem in der ersten Form,

P(H|D) = P(D|H) ∙ P(H) / P(D),

folgt sofort: P(H|D) = P(H). Die Glaubwürdigkeit H wird dann also auch nicht beeinflusst.

In beiden Fällen ist also der Verstärkungsfaktor f = 1. Interessant sind natürlich solche Fälle, in denen Faktor größer als 1 ist oder sogar sehr viel größer ist. Schauen wir uns nun an, unter welchen Umständen das passiert. Wir tun das am besten an einigen Beispielen:

Anwendungen des Bayesschen Theorems

Beispiel 1 (aus der Medizin):  

Die Hypothese sei

K:= „Der Patient hat die Krankheit K“,

Statt „H“ schreiben wir nun „K“, um uns hier an die Bedeutung von „H“ immer gut erinnern zu können. Aus gleichen Gründen schreiben wir nun „T“ für „D“. Sei also

T:= „Ein Test T auf diese Krankheit ist positiv“.

Uns interessiert dann P(K|T), d.h. die Wahrscheinlichkeit, dass die Krankheit vorliegt, wenn der Test T ein positives Ergebnis geliefert hat.

Es gibt Krankheiten, die häufig, und solche, die seltener bzw. sehr selten auftreten. Die Wahrscheinlichkeit P(K), dass ein beliebiger Patient die Krankheit K hat, nennt man die Prävalenz. Diese ist durch epidemiologische Studien bekannt. Die Werte liegen in der Regel zwischen 0.01 und 0.001. Die Wahrscheinlichkeit P(D|H) alias P(T|K), dass bei der Krankheit K das Testergebnis positiv ist, muss nahe bei 1 liegen, andernfalls wäre der Test nichts wert. Man nennt diese Größe die Sensitivität des Tests. Typische Werte liegen im Bereich 0.9 bis 0.95.

Die Größe P(T|¬K) gibt die Wahrscheinlichkeit an, dass der Test positiv ist, wenn die Krankheit K nicht vorliegt. Sie ist also ein Maß für die relative Anzahl der positiven Testergebnisse bei falscher Hypothese, für die „falsch-positiven“ Testergebnisse also. Dies ist die zentrale Größe für den Verstärkungsfaktor, dessen Kehrwert nun lautet:

1/f₁ = P(K) + (1 – P(K)) ∙ P(T|¬K) /P(T|K).

• Wäre P(T|¬K) in der Größenordnung von P(T|K), also z.B. gleich P(T|K), so wäre der Kehrwert gleich P(K) + (1 – P(K)) = 1. Damit wäre auch f = 1 und der Test wäre sinnlos.
• Würde andererseits bei Gesunden der Test nie positiv ausfallen, wäre also P(T|¬K) = 0, wäre 1/f₁ = P(K) und nach P(K|T) = f₁ ∙ P(K) schließlich P(K|T) = 1. Ein positives Ergebnis beim Test würde also mit Sicherheit die Krankheit anzeigen. Das wäre eine ideale Situation.

Die Güte des Tests hängt also entscheidend von der Wahrscheinlichkeit der „Falsch-positiven“, von der Häufigkeit eines positiven Testergebnisses bei Gesunden ab. Das ist natürlich plausibel.  Den Effekt kann man nun aber quantitativ angeben, man ist nicht auf ein Bauchgefühl angewiesen.

Statt der Wahrscheinlichkeit P(T|¬K) der „Falsch-positiven“ spricht man oft von der Spezifität P(¬T|¬K) = 1 – P(T|¬K), d.h. die Wahrscheinlichkeit, dass der Test negativ ausgeht, wenn die Krankheit K nicht vorliegt.

Bei dem berühmten PSA-Test auf Prostata-Karzinom ist z.B. P(K) = 0,0021 (0,21%). Wir nehmen für die Sensitivität P(T|K) den Wert 0,95 an und für die Spezifität P(¬T|¬K) den Wert 0,4, also P(T|¬K) = 0.6 ist. Dann ergibt sich

P(K|T) = 0,0033,

d.h. die Wahrscheinlichkeit, dass bei positivem Ergebnis des PSA-Test ein Prostatakarzinom vorliegt, ist 0,33%, nur geringfügig über der allgemeinen Prävalenz 0,21%. Das liegt daran, dass 0,6, die Wahrscheinlichkeit der „Falsch-positiven“, relativ groß ist.

Beispiel 2 (aus der Rechtsanwendung):

In einer Gruppe von 4000 Menschen kommt es zu einem Tötungsdelikt. Der Täter hinterlässt eine DNA-Spur, aufgrund derer ein DNA-Profil erstellt werden kann. Diese Daten treten bei 0,1% der Menschen auf. Bei einem Reihen-DNA-Test einige Jahre später entdeckt man eine Person X mit dem gleichen Profil und es stellt sich heraus, dass er Mitglied der Gruppe zur Zeit des Tötungsdeliktes war.

Sei

H: = „X ist der Täter“

D: = „X hat das DNA-Profil des Täters“

Aus den angegebenen Daten folgern wir:

P(H) = 1/4000, P(D|¬H) = 1/1000, P(D|H) = 1.

Es folgt P(H|D) = 1/5 = 20%.

Das ist nicht viel. P(D|¬H) ist immer noch relativ groß. Unter den 4000 in Frage kommenden Menschen darf man nämlich immerhin 4000 ∙ P(D|¬H) = 4 Personen mit einem positiven Testergebnis erwarten.

Beispiel 3:

Eine Frau erwartet ihr erstes Kind. Ihr Bruder ist Bluter, ihr Mann aber nicht. Für die a-priori Wahrscheinlichkeit, dass die Frau ein Gen für die Bluterkrankheit trägt, setzen wir an: P(H) = P(¬H) = ½. Dabei steht H für die Hypothese „Eine Frau trägt das Gen für eine Bluterkrankheit“. Nun kommt ihr Kind gesund zur Welt. Für die Daten stehe also D = „Der Sohn dieser Frau kommt gesund zur Welt.“

Der Fall D tritt bei einem Gen für eine Bluterkrankheit mit der Wahrscheinlichkeit ½ ein. Also ist P(D|H) = ½. Andererseits ist P(D|¬H) = 1, d.h. Ist das Gen nicht vorhanden, wird das Kind gesund sein. Andere Gründe für eine Krankheit sind in dieser Betrachtung nicht maßgebend.

Wie ändert sich die Wahrscheinlichkeit dafür, dass die Frau ein Gen für die Bluterkrankheit trägt, da man nun weiß, dass der Sohn gesund ist? Wie groß ist P(H|D)?

Nach dem Bayesschen Theorem gilt

P(H|D) = ½ ∙ ½ / (½ ∙ ½ + 1 ∙ ½)) = 1/3.

Die Wahrscheinlichkeit sinkt als von ½ auf 1/3. Für das nächste Kind würde man also mit dem Prior P(H) = 1/3 rechnen.

Was erhielte man, wenn das Kind als Bluter zur Welt gekommen wäre? Nun kommt die Aussage ¬D ins Spiel. Es ist P(¬D|H) = ½, P(¬D|¬H) = 0.

P(H|¬D) = ½ ½ / (½ ½ + 0∙1)) = 1,

d.h. mit Sicherheit kann man aussagen, dass die Frau das Gen trägt, wie erwartet.

Beispiel 4:

Das berühmte Ziegenproblem darf hier nicht fehlen. Es lässt sich mit folgender Situation beschreiben:

Bei einer Fernseh-Show sollen Sie eine von drei Türen auswählen. Hinter einer Tür wartet ein Auto als Preis auf Sie, hinter den anderen beiden steht jeweils nur eine Ziege. Sie zeigen auf eine Tür, nennen wir sie Tür 1.  Der Moderator, der weiß, hinter welcher Tür die Ziege steht, öffnet nun Tür 3. Eine meckernde Ziege schaut hervor. Der Moderator fragt Sie: Bleiben Sie bei Ihrer Wahl Tür 1 oder wollen Sie nun zu Tür 2 wechseln?

Die Frage: Vergrößert sich die Wahrscheinlichkeit dafür, dass Sie Auto gewinnen, wenn Sie wechseln?

Wir können dieses Problem wie einen medizinischen Test sehen: Die Hypothese ist:

H = „Das Auto steht hinter Tür 1.

Die „Daten“ zeigen:

D = „Das Auto steht nicht hinter Tür 3.

Wie sehen nun die verschiedenen Wahrscheinlichkeiten aus? Es ist

P(H) = 1/3, da es insgesamt drei Möglichkeiten gibt,

P(D) = 1/2, da der Moderator zwei Möglichkeiten hat, eine Tür zu öffnen, wo immer auch das Auto steht,

P(D|H) = 1/2, da der Moderator demnach auch zwei Möglichkeiten hat, eine Tür zu öffnen, wenn H gegeben ist.

Dann ist also P(H|D) = P(D|H) ∙ P(H)/ P(D) = 1/3.

Die a-priori-Wahrscheinlichkeit ändert sich also nicht. Das ist auch plausibel, da der Moderator nur einen Test bei Tür 3 macht.  Die Ereignisse H und „Das Auto steht hinter Tür 3“ sind aber disjunkt.

Nun folgt P(¬H|D) = 1 – P(H|D) = 2/3. Das Ereignis ¬H bedeutet: „Das Auto steht hinter Tür 2“ ∨ „Das Auto steht hinter Tür 3“, was nun gleichbedeutend ist mit: „Das Auto steht hinter Tür 2“.

Man verdoppelt also die Wahrscheinlichkeit, das Auto zu gewinnen, wenn man wechselt.

Dieses Ergebnis ist überraschend, wenn man Tür 1 und Tür 2 als zwei Möglichkeiten dafür sieht, dass ein Auto dahintersteht, nachdem der Moderator Tür 3 geöffnet hat. Dann würde man schließen, dass sich ein Wechsel nicht lohnt. So denken sehr viele und die Vorstellung dieses Problems mit der oben beschriebenen Lösung in einer amerikanischen Zeitschrift hat heftige Diskussionen ausgelöst (von Randow, 1992).

Eine solche Strategie für eine Revision von Glaubwürdigkeitsgraden aufgrund von Daten kann man anwenden, wenn mehr als zwei Ereignisräume wie H und D im Spiel sind. Um dabei den Überblick zu behalten, stellt man in einem Diagramm jeden Ereignisraum als einen Kreis dar und notiert dort auch die für eine Berechnung benötigten Wahrscheinlichkeiten. Für den einfachsten Fall, den PSA-Test sieht das dann so aus wie in Abb.1, links. Ein Pfeil von K nach T zeigt an, dass das Ereignis K das Ereignis T beeinflusst. Die Größe von Interesse, nämlich P(K|T), entspricht nun genau dem umgekehrten Pfeil (von rechts nach links).

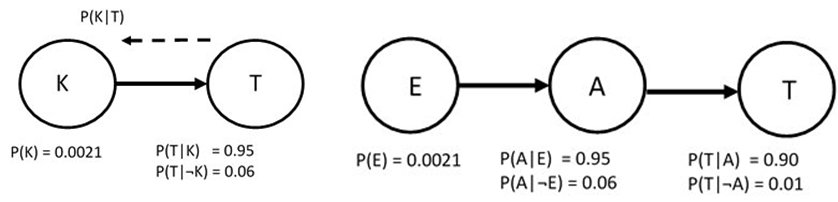
Schon etwas komplizierter ist ein Fall mit drei Zufallsvariablen (Abb. 1, rechts). Als Beispiel betrachte man dazu einen Einbruch E in ein Haus, einen Alarm A aufgrund einer entsprechenden Anlage und im Falle eines Alarms einen Anruf T des Nachbarn an den Eigentümer, der fernab von seinem Haus weilt. Die Pfeile zeigen deutlich, dass ein Einbruch, der mit der a-priori Wahrscheinlichkeit P(E) geschieht, einen Alarm mit Wahrscheinlichkeit P(A|E) auslöst, wobei es bei der Alarmanlage einen Fehlalarm mit Wahrscheinlichkeit P(A|¬E) geben kann. Der Alarm schließlich gibt mit Wahrscheinlichkeit P(T|A) Anlass für den Nachbarn, den Eigentümer aufgrund des Alarms anzurufen, während der Nachbar mit Wahrscheinlichkeit P(T|¬A) sonst anruft.  Man möchte nun von dem Ereignis eines Anrufs T auf die Wahrscheinlichkeit eines Einbruchs E schließen.

Dieses sind die einfachsten Beispiele von so genannten Bayesschen Netzen. In der Praxis stellen solche Netze eine größere Anzahl von Ereignisräumen dar und die Topologie der Netze kann höchst unterschiedlich sein. Darauf, wie die Berechnung des Einflusses der Daten auf die a-priori-Wahrscheinlichkeiten mit Hilfe des Bayesschen Theorems dann zu organisieren ist, wollen wir hier nicht eingehen. Das ist ein weites Feld, auf das wir uns hier nicht begeben wollen (siehe aber z.B. (Ertel, 2016) (Darwiche, 2009)).

Wir sollten uns an die Vorsokratiker erinnern und sehen, was aus deren Ansatz nach den Einsichten in die Möglichkeiten von logischen und dialektischen Schlüssen im Laufe der Zeit geworden ist. Was ist bis heute aus der Suche nach dem „Einen“ geworden, nachdem man sich nun weiter auf den Weg gemacht hat, suchend das „Bessere“ zu finden?