Boolesche Verbände
BLOG: Die Natur der Naturwissenschaft

Nach der Diskussion der Aristotelischen Logik und der kurzen Einführung in die Aussagenlogik soll in diesem Blogbeitrag ein Blick auf eine mathematische Theorie geworfen werden, welcher eine Struktur zugrunde liegt, die man als gemeinsame Basis der Aristotelischen Begriffslogik wie der modernen Aussagelogik erkennen kann. Gleichzeitig kann man damit auch zeigen, dass mathematische Strukturen, die zunächst nur auf der syntaktischen Ebene definiert werden, auf der semantischen Ebene verschieden interpretiert werden können. Eine Struktur kann also verschiedene „Modelle“ besitzen.
Wer kein Freund der Mathematik ist, kann dieses Kapitel überspringen; es ist für die Erzählung über die Entwicklung des Logos nicht wesentlich. Er verpasst dabei allerdings ein Erlebnis, bei welchem man an einem einfachen Beispiel den Sinn der Unterscheidung von Syntax und Semantik besonders deutlich sieht.
Die Struktur, die eine Basis für die beiden Logiken darstellt, ist die eines Booleschen Verbandes. George Boole (1815 bis 1864), ein englischer Logiker und Philosoph, führte schon im Jahre 1847 in seinem Werk The Mathematical Analysis of Logic eine formale Sprache für logische Beziehungen ein und nahm damit einen wichtigen Aspekt der späteren Aussagenlogik vorweg.
Verband
Um zu erklären, was ein Boolescher Verband ist, muss man zunächst sagen, was man heute in der Mathematik ganz allgemein unter einem Verband verstehen will (siehe z.B. (Hermes, 1967)). Wie immer in der Mathematik ist diese Struktur ein System von Zeichen, das durch bestimmte Regeln aus einem grundlegenden Satz von Zeichen aufgebaut werden kann.
Wir betrachten dazu einen Zeichenvorrat, der aus Variablen A, B, … und zwei Verknüpfungen „⊓“ und „⊔“ besteht. Wir formulieren jetzt die Regeln in unserer Umgangssprache, in der wir die Bedeutung des Gleichheitszeichens „=“ kennen. Wir müssen zunächst sagen, wie man aus diesen elementaren Zeichen bestimmte Terme, d.h. Zeichenketten konstruieren kann, die gewissermaßen die Wörter und Sätze der formalen Sprache darstellen.
Das ist nun einfach:
Mit A und B als Terme sind auch A ⊓ B, A ⊔ B, A = B zulässige Terme.
Für die Verknüpfungen sollen gelten:
A ⊓ B = B ⊓ A und A ⊔ B = B ⊔ A, also die kommutativen Gesetze,
- (A ⊓ B) ⊓ C = A ⊓ (B ⊓ C) und (A ⊔ B) ⊔ C = A ⊔ (B ⊔ C), die assoziativen Gesetze, und schließlich die Verschmelzungsgesetze:
- A ⊔ (A ⊓ B) = A und A ⊓ (A ⊔ B) = A.
Eine Menge V = {A, B, …,} mit Verknüpfungen, die solchen Regeln gehorchen, nennt man in der Mathematik ganz allgemein einen Verband. Die Klammern „(“ und „)“ sind zur besseren Lesbarkeit eingefügt oder um anzugeben, welche Verknüpfung zuerst ausgeführt werden soll.
Boolescher Verband
Um der Struktur des Booleschen Verbandes näher zu kommen, führen wir hier noch ein so genanntes Distributivgesetz ein:
A ⊓ (B ⊔ C) = (A ⊓ B) ⊔ (A ⊓ C) und A ⊔ (B ⊓ C) = (A ⊔ B) ⊓ (A ⊔ C).
Der Verband wird damit zu einem so genannten distributiven Verband.
Wir können leicht nachrechnen, dass in der Aussagenlogik, in der unter den Verknüpfungen die Symbole „∧“ bzw. „∨“ verstanden werden, diese Regeln gelten.
Halbordnung: Wir können für Zeichenketten aufgrund der geforderten Regeln eine so genannte Halbordnung einführen. Diese ist ganz allgemein eine Relation A ⊂ B für zwei Zeichenketten A und B mit folgenden Gesetzen:
A ⊂ A.
Wenn A ⊂ B und B ⊂ A, so A = B.
Wenn A ⊂ B und B ⊂ C, so A ⊂ C.
Bekannte Beispiele solcher Halbordnungen sind die Inklusion für Mengen und die Relation ≤ (kleiner-gleich) für rationale Zahlen.
Man beachte, dass wir hier nicht von einer Totalordnung reden, also nicht auch noch fordern, dass für alle A, B gilt: Entweder gilt A ⊂ B oder B ⊂ A. Es kann also Paare A, B geben, für die diese Relation „⊂“ nicht zutrifft, wie z.B. für zwei disjunkte Mengen.
Nun müssen wir sagen, wie eine Halbordnung in einem Verband realisiert sein kann: Es soll gelten:
A ⊂ B genau dann, wenn A ⊓ B = A ist.
Obere und untere Schranke: In bestimmten Verbänden kann es ein Element O geben, für das gilt
A ⊂ O für jedes Element A des Verbandes, d.h. A ⊓ O = A.
Man nennt dann O eine obere Schranke der Halbordnung.
Entsprechend gilt für eine untere Schranke U:
U ⊂ A für jedes Element A des Verbandes, d.h. U ⊓ A = U.
Solche Schranken müssen nicht unbedingt in jedem Verband existieren, z.B. gibt es für die rationalen Zahlen keine obere Grenze.
Existieren solche Grenzen, so gibt es ein kleinstes Element, das wir allgemein mit „0“ bezeichnen. Das größte Element nennen wir dann „1“.
Dann gilt also auch
A ⊓ 1 = A und A ⊔ 0 = A
für jedes A. Das sieht man leicht ein, wenn man in den Verschmelzungsgesetzen für A ⊓ ¬A den Ausdruck 0 einsetzt bzw. für A ⊔ ¬A für den Ausdruck 1.
Komplementäres Element: Eine Zeichenkette B mit
A ⊓ B = 0 und A ⊔ B = 1,
bei gegebenem A nennt man komplementär zu A, und man notiert B dann als ¬A. Dann ist auch ¬¬A = A.
Hiermit hat man nun alle Begriffe für einen Booleschen Verband beisammen: Verknüpfungsgesetze, Halbordnung, Schranken, komplementäre Zeichenkette. Man beachte, dass wir hier einen Kalkül vor Augen haben, der unabhängig von jeder Bedeutung für die Variablen A, B, … ist. Im Folgendem werden wir manchmal statt von einem „Verband“ auch von einer „Algebra“ reden. Dieser Begriff steht ja jeweils für ein System mit bestimmten Rechenregeln.
Für spätere Zwecke betrachten wir explizit den Booleschen Verband, der nur zwei Elemente enthält. Danach wollen wir einige einfache Interpretationen der allgemeinen Verbandsstruktur betrachten.
Die zweiwertige Boolesche Algebra
Die Variablen A, B, … mögen nur die beiden Zahlen 0 und 1 annehmen können. Diese müssen dann mit der unteren Schranke U bzw. oberen Schranke O identisch sein. Es muss also gelten:
A ⊓ 1 = A und
0 ⊓ A = 0
für A = 0 oder 1. Damit sind schon alle Möglichkeiten der Verknüpfung „⊓“ bestimmt.
Aus dem Verschmelzungsgesetz A ⊔ (A ⊓ B) = A erhalten wir mit A = 1:
1 ⊔ (1 ⊓ B) = 1,
woraus mit B = 1 folgt: 1 ⊔ 1 = 1, und mit B = 0: 1 ⊔ 0 = 1. Auf ähnliche Weise erhält man 0 ⊔ 0 = 0.
Das Komplement B von 1, bestimmt durch die Gleichungen
1 ⊓ B = 0 und 1 ⊔ B = 1,
ist dann 0, für das Komplement von 0 erhält man auf ähnliche Weise 1. Die Ergebnisse kann man in folgender Tafel festhalten.
| A | B | A ⊓ B | A ⊔ B |
| 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 |
Man erkennt die Wahrheitstafel der Zeichen „∧“ und „∨“ der Aussagenlogik wieder.
Diese zweiwertige Boolesche Algebra spielt eine wichtige Rolle bei der Implementierung logischer Regeln in elektronischen Rechnern (siehe z.B. Wikipedia: Logikgatter).
Die Mengenalgebra
Wir interpretieren hier die Variablen A, B, … als Teilmengen einer nichtleeren Menge M. Das Symbol „⊓“ stehe für die Durchschnittsbildung „⋂“, das Symbol „⊔“ für die Vereinigung „⋃“ zweier Mengen, ¬A ist dann das Komplement der Menge A, „0“ die leere Menge und „1“ die Menge M.
Wir sehen, wie sich alle Regeln der Mengenlehre in den Axiomen des Booleschen Verbandes widerspiegeln. Alle diese Beziehungen kann man auch veranschaulichen, indem man Mengen als Kreise darstellt, die in einander geschachtelt, überlappend oder getrennt voneinander gezeichnet sind (Abb.1).
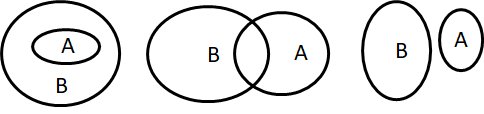
Links: A ⊂ B. Mitte: A ∩ B ≠ 0. Rechts: A ∩ B = 0. In beiden letzten Fällen stehen A und B nicht in der Relation A ⊂ B.
Die sogenannte Begriffslogik
Interpretiert man die Variablen des Booleschen Verbandes als Begriffe, so drücken die Regeln der Halbordnung des Verbandes die möglichen Beziehungen zwischen Begriffen aus.
Die Syllogismen haben wir in dem Blogbeitrag „Die Syllogismen des Aristoteles“ schon als Beziehungen zwischen Mengen, die den jeweiligen Begriffsumfang darstellen sollen, interpretiert. Die Mengenalgebra ist nach dem vorherigen Abschnitt also eine Interpretation eines Booleschen Verbands. Das Gleiche gilt dann auch für die Aristotelische Begriffslogik.
Der Syllogismus „Barbara“ entspricht dann dem 3. Gesetz der Halbordnung. Der Syllogismus „Celarent“ wird durch
Wenn B ∩ C = 0 und A ⊂ C, so B ∩ A = 0
dargestellt. In dem Kalkül, den die Gesetze des Booleschen Verbandes bereitstellen, lässt sich diese Konklusion so beweisen:
Wenn A ⊂ C, so C ∩ A = A.
Dann ist
B ∩ A = B ∩ (C ∩ A) = (B ∩ C) ∩ A = 0 ∩ A = 0,
wobei wir das Assoziativgesetz benutzt und die Prämisse B ∩ C = 0 berücksichtigt haben sowie die Tatsache, dass für die untere Schranke 0 gilt: 0 ⊂ A. Damit folgt dann 0 ∩ A = 0.
Die Aussagenlogik
Wenn wir die Elemente des Booleschen Verband als Aussagen betrachten, und für diesen Verband dazu noch eine Abbildung auf einen zweiwertigen Booleschen Verband mit den Elementen 0, 1 einführen, haben wir eine Struktur vor uns, die wir als Aussagenlogik interpretieren können (Hermes, 1967, p. 162ff).
Wir betrachten also zunächst einen Verband mit den Symbolen A, B, …, die wir nun als Aussagen interpretieren. Die Verknüpfung ⊓ wird in „∧“ übersetzt sowie „⊔“ in „∨“. Das Komplement von A wird als Negation ¬A interpretiert und die Konstante 1 wird zur Tautologie „⊤“, die Konstante 0 zum Widerspruch „⊥“. Diese sind keine speziellen Ausdrücke, sondern stellen jeweils eine Klasse von Ausdrücken dar.
Die Verschmelzungsgesetze lauten nun
A ∨ (A ∧ B) = A und A ∧ (A ∨ B) = A.
Die Tautologie ist eine obere Schranke, für jeden Ausdruck A gilt
A ∧ ⊤ = A,
während der Widerspruch eine untere Schranke ist:
⊥ ∧ A = ⊥.
Andere Aussagen B, die mit A in der Relation A ∧ B = B stehen, gibt es nicht.
Damit ist die Interpretation des Booleschen Verbandes abgeschlossen. Nun konstruieren wir die Abbildung dieses Verbandes auf einen zweiwertigen Booleschen Verband, wie wir ihn oben, nach der Einführung des allgemeinen Booleschen Verbandes, beschrieben haben.
Bezeichnen wir diese Abbildung mit f, so soll nun das Bild f(A) einer Aussage A einem Element der zweiwertigen Booleschen Algebra entsprechen, also gleich 0 oder 1 sein, was wir als falsch bzw. als wahr interpretieren. Diese Abbildung soll „homomorph“ sein; das bedeutet, dass die Symbole für die Negation und die Verknüpfungen in die entsprechenden Symbole des zweiwertigen Booleschen Verbandes übergehen. Es soll also gelten:
f(¬A) = ¬f(A),
f(A ∧ B) = f(A) ⊓ f(B) und f(A ∨ B) = f(A) ⊔ f(B).
Wir stellen fest, dass damit das Bild der Gleichungen der Aussagenlogik mit den Gleichungen der zweiwertigen Booleschen Algebra übereinstimmen:
Aus den Bestimmungsgleichungen für die untere und obere Schranke folgt
- f(A ∧ ⊤) = f(A) ⊓ f(⊤) = f(A),
für f(A) = 1 folgt also f(⊤) = 1.
- f(A ∨ ⊥) = f(A) ⊔ f(⊥) = f(⊥),
für f(A) = 0 folgt also f(⊥) =0.
Um zu sehen, wie das Bild einer Aussage A mit dem Bild von ¬A zusammenhängt, betrachten wir das Bild der beiden Gleichungen, die die komplementäre Zeichenkette bestimmen:
- f(A ∧ ¬A) = f(A) ⊓ f(¬A) = f(⊥) = 0,
- f(A ∨ ¬A) = f(A) ⊔ f(¬A) = f(⊤) = 1.
Die Symbole 0 und 1 sind hier Elemente der zweiwertigen Booleschen Algebra.
Aus der ersten Gleichung folgt: Ist f(A) = 1, so f(¬A) = 0. Aus der zweiten Gleichung folgt: Ist f(A) = 0, so f(¬A) = 1.
Wir entdecken: In der Diskussion der Aussagenlogik haben wir diese Abbildung auf eine zweiwertige Boolesche Algebra immer unbewusst vollzogen. Die Symbole in den Wahrheitstafeln stehen also immer für die Abbilder der Aussage der entsprechenden Spalte. Hier wird nun explizit gemacht, was wir dabei eigentlich getan haben.


Wenn ich das richtig verstehe, dann konstruiert die Boolsche Algebra den Zusammenhang von logischen Gesetzen zu den Gesetzen der Algebra. Das Ganze kann dann anschaulich gemacht werden, durch die Venn- Diagramme.
Test: Die Definition einer unteren Schranke bezeichnet man mit 0, die obere Schranke mit 1.
Darf man daraus schließen, dass im Zahlenraum N , die 0 die kleinste Zahl ist ?
Zitat: „Diese zweiwertige Boolesche Algebra spielt eine wichtige Rolle bei der Implementierung logischer Regeln in elektronischen Rechnern (siehe z.B. Wikipedia: Logikgatter).“
Laut Warren McCulloch spielt diese zweiwertige Boolesche Algebra grundsätzlich auch eine wichtige Rolle bei der Implementierung logischer Regeln in biologischen neuronalen Netzen. Dies würde auch im Prinzip (mit gewissen Einschränkungen auf die ich eingehen möchte) die Informationsverarbeitung in derartigen Netz erklären. Die nachstehende Sicht enthält meine persönliche Interpretation.
Der Unterschied zwischen „Technik“ und „Biologie“ ist offensichtlich.
Bei der technischen Realisierung der Verknüpfungen ist z.B. die “UND” Gatterfunktion „absolut“ determiniert.
Sie ist genau dann erfüllt, wenn alle Eingänge gleichzeitig logisch “1” sind.
Damit ist auch ein Konstrukt aus vielen Gatterschaltungen determiniert, kurz gesagt, man erhält prinzipiell immer die gleichen Ergebnisse.
Dies ist offensichtlich bei biologischen neuronalen Netzen nicht so.
Der Grund ist offensichtlich, dass ein Neuron nicht „absolut stabil“, abhängig vom Signalinput auf den Eingängen (Dendriten) triggert.
Es triggert dann, wenn auf möglichst vielen Eingängen möglichst gleichzeitig Impulse einlangen, die das Neuron zum Triggern bringen können.
Es müssen auf „qualifiziert“ vielen Eingängen (nicht unbedingt allen) ausreichende Impulsladungen eintreffen.
Es gibt so etwas wie „Mehrheitsentscheidungen“. Triggern viele Neuronen, die redundant einen (gelernten) Sachverhalt abbilden, so gibt es eine qualifizierte und eine sicher „Mehrheitsentscheidung“. Andernfalls eben eine unsichere oder falsche Entscheidung.
Es gilt sozusagen: 3 Verfassungsjuristen 4 Rechtsmeinungen.
McCulloch hat eine Möglichkeit zur Realisierung der „Nichtfunktion“ aufgezeigt. Die Verneinung kann aber auch so realisiert werden, indem man davon ausgeht dass die Verneinung von „heiß“ (von einem anderen „Rezeptor“) „kalt“ stammt. Statt dem (invertierten) Signal „nicht heiß“ nutzt das System z.B. das Signal „kalt“ zur weiteren Verknüpfung.
Die Turing Berechenbarkeit wurde nachgewiesen. Das System ist offensichtlich hoch kaskadierbar und in der immensen Komplexität der Neuronenverbände kann das „Wissen“ und das „Verhalten“ des Systems vermutlich voll abgebildet werden.
Bei der technischen Realisierung legt der Konstrukteur des Systems die Verknüpfungspunkte fest, in der Biologie bilden sich die Verknüpfungspunkte gemäß dem Konzept von E. Kandel automatisch.
Empfindungseffekte dürften an elektrisch chemischen Schnittstellen entstehen. Vielleicht durch “Resonanzeffekte” bei den chemischen Bindungen.
Bewusstseinsinhalte könnten an besonderen neuronalen Strukturen z.B. End- und Zwischenschichten wie Netzthaut, Hirnhaut, …. als so etwas wie Zwischen/Endergebnisse von Verarbeitungsprozessen, informell (z.B. als gleichzeitige Triggerprozesse) „abgebildet“ werden.Vergleichbar einem Bildschirm, Leinwand, Mattscheibe…
Mit dieser ganz groben Übersicht möchte ich einer zusammenfassenden Erklärung der elektrischen Informationsverarbeitung im neuronalen System möglichst nahekommen.
Natürlich könnte man dies auch als „unterkomplex“ sehen, weil viele auch wichtige, insbesondere biologische Aspekte, hier nicht berücksichtigt sind.
Allerdings dürfte es darüber ohnehin relativ viel an Literatur geben.
Dieses Konzept geht auf W. McCulloch (Neurologe 1943) und E. Kandel zurück. Wobei ich vermute, dass McCulloch auf frühere Konzepte von Physikern und Norbert Wiener (Kybernetiker) aufbauen dürfte.
Mich würde die Sicht der „modernen Physik“ zu diesen Konzepten interessieren.
Meine persönlichen Interpretationen stammen aus normalen Grundlagenwissen aus Elektronik/Informatik.
@Elektroniker: Vielen Dank für den interessanten Beitrag. Könnte da nicht eine mehrdimensionale Boolesche Funktion mit Argumenten aus {0,1} gute Dienste tun für ein Modell eines biologischen Gatters? Es gibt sicher auch schon künstliche neuronale Netze mit solchen Funktionen. Ich habe aber keinen Überblick über die entsprechende Literatur. Meine Beschäftigung mit solchen Netzen ist schon etwa 15 Jahre her.
@bote19:
Was haben die natürlichen Zahlen denn hier zu tun? Die untere Schranke muss einen Namen haben, dafür nehmen wir das Symbol “0”. Dass die Rolle dieses Symbols und die Rolle der Zahl “0” sich in ihrer jeweiligen mathematischen Umgebung ähneln, ist eine andere Sache.
Josef Honerkamp
dumme Fragen haben oft einen berechtigten Hintergrund. Unser Mitkommentator Chry hat ja auch schon bemängelt, dass ich mich nicht an die Systematik halte. Das war mir schon klar, dass dass das “Symbol 0” in der Algebra als Mengenbezeichnung verwendet wird.
Im Dualsystem kann man das Symbol 0 als Zahl betrachten, aber wie es der Computer auch macht, schon als Schaltzustand low (bedeutet 0,7 Volt Spannung am Ausgang des Gatters) im Gegensatz zu high (5 Volt), der dann mit 1 beschrieben werden kann.
Die Rechengesetze der natürlichen Zahlen (Kommutativ., Assoziativ, Distributivgesetz werden von Bool auf die Logik angewendet, die er dann Verbände nennt.
Und da wir ja mit den Bezeichnungen A und B auskommen wollen, müssen wir begründen, dass wir damit auskommen können.
Das geschieht durch die obere und untere Schranke.
Die obere Schranke ist 1 und die untere Schranke ist 0.
Und wie wir später bei der Schaltalgebra sehen , kann man die 1 sowohl als Zahl als auch als Logikzustand betrachten. Mit der 0 ist es genau so.
Und wenn wir jetzt noch alle Zahlen n als 1/n darstellen, dann passen alle n in das Intervall zwischen 0 und 1.
Die untere Schranke in der Logik wird mit 0 bezeichnet und die untere Schranke der Zahlen in der Darstellung 1/n ist auch die kleinste Zahl.
Deswegen meine Frage, „kann man aus der logischen Untrschranke 0 schließen, dass die Zahl 0 die kleinste Zahl sein muss“ ?
Die Frage ist ernst gemeint
@bote19:
Die Null ist ein Symbol, welches in vielen mathematischen Strukturen verwendet wird und dort jeweils eine bestimmte Bedeutung hat. Im Zahlenraum der natürlichen Zahlen ist die Null die kleinste Zahl, im Zahlenraum der rationalen Zahlen ist das nicht der Fall, und im Booleschen Verband ist die Null gar keine Zahl. Sie können nicht einfach von einer Struktur zu eines anderen springen, das ergibt keinen Sinn.
Josef Honerkamp,
wenn Sie unterscheiden zwischen der Zahl und dem Zahlzeichen , dann ist das ja korrekt.
Und Sie haben ja auch erkannt dass ich von einer Struktur zur anderen springe. Genau das ist ja meine Absicht.
Ist die Struktur des Zahlenraumes zwischen 1 und 0 die gleiche wie im Boolschen Verband ?
Wir können ja die logischen Beziehung zwischen A und B durch C,D, E …….genau so verlängern wie wir eine Zahlenreihe verlängern.
Ganz konkret , ich wollte die 0 in der Algebra logisch begründen.
Dabei lasse ich es jetzt mal bewenden.
…
Die Mengenalgebra
Wir interpretieren hier die Variablen A, B, … als Mengen, Das Symbol „⊓“ stehe für die Durchschnittsbildung „∩“, das Symbol „⊔“ für die Vereinigung „∩“ zweier Mengen, ¬A ist dann das Komplement der Menge A, „0“ die leere Menge und „1“ die allumfassende Menge.
…
– sollte das Symbol für die Vereinigung nicht “U” sein ?..
Ansonsten: finde ich schön mit solchen Texten mal wieder “altes Wissen” aufzufrischen ! Danke für die mathematischen Erläuterungen, werde weiter mitlesen
@Boolesche Verbände
Anscheinenden führen ihre Ausführungen darauf hinaus, dass das Rechnen mit natürlichen und rationalen Zahlen gemeinsame formal-mathematischen Wurzeln mit der Aussagenlogik hat. Das finde ich interessant.
Dass das alles in der Wirklichkeit nutzbar ist, spricht dafür, dass in der Wirklichkeit die entsprechenden mathematischen Strukturen vorhanden sind. Beim einfachem Rechnen mit natürlichen Zahlen, kann man das gut sehen, wenn man z.B. mit verschiedenen Körben mit Äpfeln drin arbeitet. Die Rechenregeln brauchen die Eigenschaft der Wirklichkeit, das keine Äpfel zwischendurch verschwinden oder sich neu materialisieren. Wenn hierfür gewisse Wahrscheinlichkeiten bestehen, wird es komplizierter.
Zu dem Beispiel mit dem Regen fällt mir ein, dass es in der Wirklichkeit auch unklar sein kann, ob es geregnet hat. Wenn es nur etwas getröpfelt hat, oder nur am Wohnort aber nicht im Zoo, kann man hier nicht einfach wahr oder falsch sagen. Die entsprechende Logik müsste irgendwie Wahrscheinlichkeiten berücksichtigen, wenn man existenten Unsicherheiten Rechnung tragen will. So geht das Problem dann von der Aussagenlogik direkt in die Wahrscheinlichkeitsrechnung über.
Ein Witz: Es watscheln drei Enten lang. Die Erste Ente sagt: Ich gehen vor zwei Enten. Die zweite Ente sagt: ich gehe zwischen zwei Enten. Die dritte Ente sagt: ich gehe auch zwischen zwei Enten.
Wir geht das?
Die dritte Ente lügt.
So wird es wieder mal komplizierter.
@Tobias Jeckenburger:
Genau, darauf komme ich bald.
@Josef Honerkamp
In dem von sf2019 (17. April 2019 @ 08:53) zitierten Textabschnitt wäre in der Tat ein “cap” durch ein “cup” zu ersetzen:
»Wir interpretieren hier die Variablen A, B, … als Mengen, Das Symbol „⊓“ stehe für die Durchschnittsbildung „∩“, das Symbol „⊔“ für die Vereinigung
„∩“„∪“ zweier Mengen, ¬A ist dann das Komplement der Menge A, „0“ die leere Menge und „1“ die allumfassende Menge.«Bei der Gelegenheit möchte ich dazu noch ein sprachliche Präzisierung vorschlagen, denn zum einen bezeichnen die Variablen A, B, … hier nicht einfach irgendwelche Mengen, und zum anderen ist die Wendung “allumfassende Menge” zumindest missverständlich und nicht lehrbuchtauglich. Dies liesse sich beispielsweise mit den nachfolgend fett gesetzten Änderungen ausräumen:
“Wir interpretieren hier die Variablen A, B, … als Teilmengen einer nichtleeren Menge M, Das Symbol „⊓“ stehe für die Durchschnittsbildung „∩“, das Symbol „⊔“ für die Vereinigung „∪“ zweier Mengen, ¬A ist dann das Komplement der Menge A, „0“ die leere Menge und „1“ die Menge M.”
Ein praktisches Beispiel zur „Tautologie“ möchte ich noch aus meiner Erinnerung beisteuern.
Vor einigen Jahrzehnten hat ein katholischer Bischof, ich glaube in einer Pfingstpredigt der ich im Autoradio zufällig zugehört habe, die zwingende Existenz Gottes als eine Art „transzendentes Objekt“ tautologisch begründet.
Er meinte, „Gott“ als Bezeichner für eine Art „transzendentes Objekt“ existiert ganz genau so wie es sich wirklich verhält. Alle „wirklichen“ Naturgesetze, alle Prozesse und alles was sonst noch im Zusammenhang mit dem was wir „Schöpfung der Welt“ nennen steht, „existiert“ genau so wie es sich eben wirklich verhält.
Das Problem ist nur, dass wir es nicht vollständig, vielleicht auch nur zum kleinen Teil wirklich „verstehen“. Die Aussage ist in jedem Fall logisch korrekt und muss auch stimmen. Es verhält sich so, wie auch bei anderen transzendenten Objekten.
Widersprüche kann es in komplexen Systemen immer wieder geben.
Bei der Erstellung eines Computerprogramms in der Informatik muss man extrem darauf achten, alle zu verknüpfenden „Variablen“ zunächst korrekt und widerspruchsfrei zu deklarieren um sie danach genau so korrekt und widerspruchsfrei zu verknüpfen. Kleinste Fehler oder Ungenauigkeiten können sich extrem auswirken.
Beim „Theodizee Problem“ werden praktisch widersprüchliche „Unterstellungen“ verknüpft und zieht daraus falsch Schlussfolgerungen.
Es würde mich trotzdem interessieren, ob man derartige Aussagen logisch „zerpflücken“ kann.
@Chris:
Ja, ich hab’s so geändert, kannte das so auch aus dem Buch von Hermes, den ich übrigens früher noch kurz als Kollegen gekannt habe. Ich wollte dem Leser nicht auch noch “Teilmengen” zumuten. Aber das ist falsche Rücksichtnahme.
@Elektroniker
„Er meinte, „Gott“ als Bezeichner für eine Art „transzendentes Objekt“ existiert ganz genau so wie es sich wirklich verhält.“ Auch wenn das ein katholischer Bischof sagte, dem würde ich ganz klar zustimmen. Wir wissen kaum, womit wir es zu tun haben. Aber was ist, das ist eben.
Wenn man immer nur Regelmäßiges erforscht, muss man sich nicht wundern, wenn alle Einmaligkeit und Transzendenz davon nicht erfasst wird. Es gibt viele Menschen, die in ihrer Erfahrungswelt auch nichts Transzendentes selbst erfahren. Für die ist das Vorgehen der Wissenschaft zunächst keine Einschränkung.
Aber für Menschen, die durchaus spirituelle Erfahrung in ihrem eigenem Leben machen, und insbesondere wer fast alltäglich am Wunder des Lebens teilzunehmen glaubt, sieht hier wohl einen Mangel im Vorgehen der Wissenschaft. Das Problem ist hier nicht die Evidenz von Fakten und Messkampangen, und auch nicht die mathematische Beschreibbarkeit dieser Messergebnisse. Wenn die spirituelle Erfahrung aber eine Entsprechung in der Wirklichkeit hat, muss diese auch irgendwo zwischen den physikalischen, biologischen und psychologischen Theoriegebäuden seinen Platz haben.
Eben genau so, wie es ist. Wenn man da überhaupt nicht nach guckt, wird man da mit Sicherheit wenig finden. Das muss nicht so bleiben. Wenn wir mal das Konnektom des menschlichen Gehirns entschlüsselt haben, könnte sich zeigen, ob unser lokales Bewusstsein nur Gehirninhalt ist, oder doch mit kosmischem Bewusstsein verbunden ist. Je mehr die Erforschung des Regelmäßigen fortschreitet, desto mehr grenzt sich auch der Bereich ein, in dem das Spirituelle in der Wirklichkeit gesucht und gefunden werden kann.
Inwieweit hier dann noch was verstanden werden kann, wird man dann sehen, wenn man hier Fakten gefunden hat. Die Fakten der Relativitätstheorie und der Quantenphysik sind ja bereits von den meisten Menschen leider nicht mehr zu verstehen. Selbst die hier diskutierte Logik wird nicht von jedermann verstanden. Das ändert aber nichts an ihrer Gültigkeit, und auch nichts an ihrer immens nützlichen Verwendbarkeit.
Tobias Jeckenburger
Das Thema „Spiritualität“ gehört, anders als die elektronische Datenverarbeitung, nur am Rande zum Thema „Boolsche Verbände“. Obwohl auch hier im Sinne von McCulloch, die Funktionen „logischer Gatter“ grundlegend sind und man so der Erklärung der Information verarbeitenden Prozesse (abgesehen vom „Empfindungsphänomen“) auch im Gehirn näher kommt.
„Spiritualität“ wird in neuronalen Systemen durch die neuronale Informationsverarbeitung realisiert. Es werden die Information abbildenden Signale aus der Sensorik (auch aus der die Empfindungen abbildenden Sensorik) mit Signalen aus den letztlich das „Bewusstsein“ abbildenden Strukturen verknüpft und nehmen so Einfluss auf das „Bewusstsein“.
In der elektronischen Informationsverarbeitung wird die Boolsche Algebra „exakt“ angewendet. Deswegen erhält man (abgesehen vom Störungsfall) immer die absolut genau gleichen Rechenergebnisse, wenn die verknüpfenden Operationen absolut gleich realisiert werden.
Die „Wahrheitstabellen“ der Gatterlogik werde zu 100% eingehalten.
In der neuronalen Informationsverarbeitung wird die Boolsche Algebra „annähernd“ angewendet.
Erst wenn in mehreren Gatteranordnungen beim intensiven Lernen die Wahrheitstabellen auch nur annähernd, sagen wir einmal zu 90 % eingehalten werden, ergeben sich „halbwegs sichere“ Aussagen.
Die Technik, besonders die Elektronik, bemüht sich in Zusammenarbeit mit anderen Fachgebieten, besonders der Chemie und Physik, möglichst viele Prozessabläufe in der Natur zunächst elektronisch, danach mit den Mitteln der Mathematik/Informatik „informell abzubilden“ um daraus möglichst Nutzen zu ziehen.
Auch die „Spiritualität“ wird immer mehr zu einem „Objekt“ der Informationsverarbeitung werden.
Es ist eine Definitionsfrage was man unter „kosmischem Bewusstsein“ versteht, wie es auch die Frage des „menschlichen Bewusstsein“ ist.
Es ist auch die Frage ob man „Bewusstseinskomponenten“ nur innerhalb einer bestimmten Person verknüpft, oder darüber hinaus mit mehreren Menschen einer oder verschiedener Gruppen, oder womöglich sogar die Tier- und Pflanzenwelt einbeziehen möchte. Im Extremfall man womöglich den Atomaren/Molekularen Prozessen z.B. in Steinen „Bewusstsein“ zubilligen möchte? Steine dürfte jedenfalls keine relevanten Mechanismen „eingebaut“ haben um mit der Nachbarschaft zu kommunizieren.
Zitat: „….ob unser lokales Bewusstsein nur Gehirninhalt ist, oder doch mit kosmischem Bewusstsein verbunden ist.“
Bewusstsein dürfte auf (besondere) Prozesse aufbauen. Diese Prozesse sind meistens verknüpft. Es ist die Frage wo man die (willkürliche) Grenze zieht (Mensch – Gruppe – Tier und Pflanzenwelt…).
Zitat: „Aber für Menschen, die durchaus spirituelle Erfahrung in ihrem eigenem Leben machen, und insbesondere wer fast alltäglich am Wunder des Lebens teilzunehmen glaubt, sieht hier wohl einen Mangel im Vorgehen der Wissenschaft. Das Problem ist hier nicht die Evidenz von Fakten und Messkampangen, und auch nicht die mathematische Beschreibbarkeit dieser Messergebnisse. Wenn die spirituelle Erfahrung aber eine Entsprechung in der Wirklichkeit hat, muss diese auch irgendwo zwischen den physikalischen, biologischen und psychologischen Theoriegebäuden seinen Platz haben.“
Für die spirituelle Erfahrung wird immer Platz sein. Erleben muss sie der Mensch selber, aber man wird sie immer besser erklären können.
Danke sehr für ihre interessanten Ausführungen.
Was mich stört, dass man in der Mathematik von Semantik spricht. Ich weiss, das wird so gemacht, insbesondere in der Modell-Theorie und in der Metamathematik. Aber mir scheint das mehr Metaphysik als Wissenschaft zu sein.
Semantik kommt ins Spiel, wenn gewisse Zeichen, Aussagen eine Bedeutung haben. Das haben sie aber in der reinen Mathematik nicht. Auch die natürlichen Zahlen haben keine Bedeutung, sie werden rein formal/syntaktisch definiert; erst wenn wir sie beispielsweise für einen Zählvorgang verwenden, erhalten sie eine Bedeutung.
Wir müssen also die Mathematik anwenden, beispielsweise in der Physik/Ökonomie, um zu einer Bedeutung zu gelangen. Tarski hat Mathematik als die Theorie der deduktiven Systeme definiert. Es ist das Wesen der Mathematik rein syntaktisch zu sein.
Mathematik ist in jedem Universum richtig, weil alles axiomatisch definiert und abgeleitet wird – es sind bedeutungslose Zeichenketten. Eine Bedeutung erhalten mathematische Strukturen (beispielsweise eine Boolsche Algebra) nicht, wenn man sie in Beziehung zu einer anderen formalen Struktur (beispielsweise Aussagenlogik) setzt.
Wahr und Falsch gibt es in unserer empirisch erfassbaren Welt nicht, nur mehr oder weniger wahrscheinlich. Deswegen bin ich sehr gespannt auf ihre weiteren Ausführungen.
Bruno Koller,
“wahr und falsch” sind nicht wörtlich zu verstehen. In der Literatur werden da auch stellvertretend ja und nein, 1 und 0, low und high verwendet, und wie Sie schon richtig gesagt haben ergeben diese Zeichen erst im Kontext ihren Sinn.