Lehrerfrage: Was sind Schwarze Löcher?
BLOG: Uhura Uraniae

Kürzlich rief Andreas Müller Lehrende von Schulen auf, Fragen zu stellen, wie man “harte Physik” auf Schulniveau erklären könnte. Die Frage, die ich wohl mit am häufigsten beantworten muss, ist die, was Schwarze Löcher sind.
Hier meine Interpretation:
Ein Schwarzes Loch ist ein Objekt (in einfachster Lösung der Gleichungen perfekt kugelförmig, weil abstrakt-mathematisch), von dem nicht einmal das Licht wegkommt, was der schnellste Bote des Universums ist. Dazu braucht man – oberflächlich betrachtet – nur klassische Newtonsche Physik und daher wurden derlei Körper auch bereits 1796 von dem französischen Mathematiker Pierre Simon Laplace als “corps obscur” postuliert. Damit kriegt man eine erste (allgemeinverständliche) Näherung an das Phänomen und eine exaktere Näherung an die Natur durch Lösung der ART-Gleichungen.
Streng genommen besagt Newtons Physik nur, dass Gravitation von Massen auf Massen wirkt und es ist zunächst nicht offensichtlich, dass Gravitation auch auf Licht wirkt – zumindest solange man nicht weiß oder bezweifelt, ob Licht eine Masse hat.
Der Clou bei Einstein (übrigens bereits 1911) ist, dass er dieses fehlende Bausteinchen lieferte. Einstein begründete in einem Artikel “über die Schwere der Energie” von 1911 sinngemäß, dass man diese unten ausführlicher geschilderte didaktische Vereinfachung hier unternehmen darf, um das Phänomen an sich zu verstehen (auch wenn man damit noch nicht exakt rechnen kann). Einstein schreibt sinngemäß: Photonen haben zweifelsfrei eine Energie E, nämlich die Energie E=h*f (Photoeffekt, d.h. auf dieser berühmten Formel beruht unsere gesamte Solartechnologie – Nobelpreis 1921) und jede Energie E hat (mit der berühmten Formel aus der SRT) E=mc² ein Masseäquivalent. Wenn nun das Photon keine Ruhmasse hat, so hat es doch ein Masseäquivalent, das wir als träge Masse interpretieren können. Daher dürfen wir das Newtonsche Gesetz auch auf Photonen anwenden, deren Masse m folglich m = h*f/c² ist.
Erst vier Jahre später sah Einstein ein, dass man so “nur” die Erlaubnis / Begründung für Laplace’ Argumentation gibt und dass der tatsächliche physikalische Gravitatioseffekt mit der ART besser, d.h. “richtiger” berechenbar ist. Dennoch wollen wir hier fürs Schulniveau anschaulich weiter argumentieren:
Newton-Laplace ausführlicher:
Wenn man von der Erde in eine Erdumlaufbahn starten will, dann braucht man dazu eine Rakete: Sie ist schneller als ein gewöhnliches Auto, das niemals die erforderliche Fluchtgschwindigkeit erreicht.
Die Fluchtgeschwindigkeit lässt sich übrigens mit der Mathematik der 9. Schulklasse leicht herleiten, denn man braucht nur den Energiesatz und muss Wurzeln ziehen können.
Wenn man umgekehrt vom Mond zur Erde starten will, dann braucht unsere Rakete weniger Schub, weil vom Mond (der weniger Masse hat als die Erde und kleiner ist) eine geringe Fluchtgeschwindigkeit benötigt.
Diese beiden Fakten sind inzwischen aus der praktischen Raumfahrt bekannt. Nun spielen wir diesen Gedanken in die andere Richtung: Wenn wir einen größeren Körper als die Erde haben – also z.B. eine Rakete von Jupiter oder der Sonne starten wollten – dann bräuchten wir eine schnellere Rakete. Die Fluchtgeschwindigkeit ist von diesen Körpern ja größer.
Wenn wir nun das Gravitationspedal in unserem Gedankenexperiment weiter durchtreten, können wir uns auch einen Körper vorstellen, von dem unsere Rakete nur mit Lichtgeschwindigkeit wegkäme.
Dieser Körper, von dem die Fluchtgeschwindigkeit der Lichtgeschwindigkeit ist, ist noch sichtbar – denn das Licht kommt ja noch weg.
ABER
Wenn jetzt auch nur ein Staubkorn dazu kommt, dann ist die Fluchtgeschwindigkeit unseres Körpers um ein Epsilon größer als die Vakuumlichtgeschwindigkeit. Ab diesem Augenblick kommt das Licht nicht mehr davon weg, denn es kann ja nicht schneller sein als c. Da aber auch nichts anderes im Universum schneller sein darf als c (das folgt aus dem Wurzelterm bereits in der Speziellen Relativitätstheorie), kommt tatsächlich nichts mehr von diesem Körper weg. 
Der Grund ist also, dass man nichts im Universum auf so große Geschwindigkeiten beschleunigen kann, die c übersteigen.
Fazit:
Schwarze Löcher sind also schwarz im physikalischen Sinn, weil kein Licht von ihnen
wegkommt (per definitionem). “Löcher” sind sie demnach höchstens in unserem Wissen, weil es ja keine Möglichkeit gibt, ihr Inneres zu ergründen:
Wer hineinfliegen würde, um zu schauen, was hinter der “magischen Grenze” dieser Kugeloberfläche (Ereignishorizont) ist, von der das Licht nicht wegkommt, der käme ja selbst auch nicht von dort weg und könnte sein Wissen niemandem mitteilen. Unsere üblichen astronomischen Methoden der berührungsfreien Fernabtastung 😉 funktionieren aber auch nicht, weil ja keine elektromagnetische Welle (Licht) von dort wegkommt.
(Von ungesunden Konsequenzen aufgrund der Gezeitenwirkung sehen wir hier mal ab, wir machen schließlich kein Medizin-Seminar, sondern Physik.)
Natürlich sind Schwarze Löcher keine “kosmischen Staubsauger“, die also alles in sich hineinsaugen: Sie tun einem nichts, so lange man ihnen eben bloß nicht zu nahe kommt. Jede Masse zieht andere an und daher ist es z.B. auch ziemlich ungesund, wenn man in einem Flugzeug (oder Raumschiff) der Erde zu nahe kommt; dann stürtzt man nämlich aufgrund der Gravitationswirkung darauf ab. Das Schöne ist: Auf der Erde kann man seine Maschine reparieren und dann weiterfliegen. – Das geht eben bei einem Schwarzen Loch nicht. 
Übrigens:
Nach Einsteins Allgemeiner Relativitätstheorie (ART) wird dieser Effekt ein wenig anders skaliert. Erst mit der modernen Physik und der Science Fiction wurden daher die Schwarzen Löcher so richtig populär.
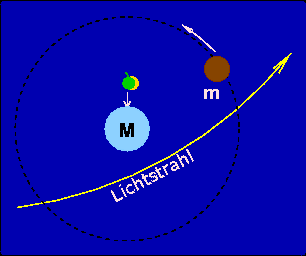
Nach der ART wirkt die Schwerkraft (Gravitation) nicht nur von einer Masse zur anderen, sondern auch auf Licht. Es versucht also zu dem massereichen Körper hinzufallen, doch weil es eben Licht ist und nicht eine wirkliche Masse wie Newtons Apfel, plumpst es nicht wirklich auf den Körper drauf, sondern wird nur ein wenig zu ihm gelenkt. Wenn es ihm also nicht zu nahe kommt, propagiert der Strahl weiter und ändert nur seine Richtung – und zwar desto mehr, je näher es an der Masse vorbei geht.
Das führt auf den Gravitationslinseneffekt, bei dem das Licht entfernter Lichtquellen gebündelt und verstärkt werden kann, so dass ferne Lichtquellen beobachtbar werden, die man anders nicht sehen würde. An dieser Stelle werde ich demnächst weiter machen, wenn ich in meinem Blog die versprochenen Exoplaneten und ihre Jagdmethoden weiterdiskutiere.
Ich hoffe, es ist mir gelungen, mit diesen Ausführungen wenigstens die Idee zu skizzieren und der Öffentlichkeit die Angst vor diesen seltsamen “Tierchen” nehmen – wenngleich man natürlich die Physik auch komplizierter machen kann.


Welche Bedeutung hat die Singularität für ein schwarzes Loch? kann es einen Ereignishorizont ohne Singularität geben? gibt es außer theoretischen Modellen auch messtechnische Erkenntnisse über die innere Struktur eines schwarzen Lochs?
Newtonsche Schwarze Löcher
Aus meiner Sicht ist dieser Text problematisch.
Zum einen verspricht die Beschreibung mehr, als das Newtonsche Modell halten kann. Im Text klingt es so, als ergäbe sich im Vergleich von klassischer Physik und Allgemeiner Relativitätstheorie der gleiche Effekt, nur “ein wenig anders skaliert”.
Konkret wird dann argumentiert, selbst Licht käme von einem Körper, bei dem die Fluchtgeschwindigkeit größer als die Lichtgeschwindigkeit ist, “nicht weg”. Kurz danach wird ausgeführt, was mit dem nicht-weg-kommen gemeint ist: es gebe eine “magische Grenze”, eben den Ereignishorizont des Schwarzen Lochs.
In der Allgemeinen Relativitätstheorie gibt es tatsächlich den Horizont des Schwarzen Lochs als Grenzfläche, die einen Raumbereich einschließt, aus dem es kein Entkommen gibt.
Aus der Newtonschen Rechnung ergibt sich allerdings kein solcher abgegrenzter Innenbereich. Dass die Fluchtgeschwindigkeit größer als die Lichtgeschwindigkeit ist, heisst ja lediglich, dass ein Teilchen, das von der Oberfläche aus mit einer Anfangsgeschwindigkeit kleiner als die Lichtgeschwindigkeit nach oben geschossen wird und dann hilflos dem Einfluss der Gravitation ausgeliefert ist, nicht ins Unendliche entkommen kann. Aus der Nähe des Objekts kann es aber zwischenzeitlich sehr wohl entkommen. Es kann sich, je nach Anfangsgeschwindigkeit, immer noch weit von dem angeblichen “Schwarzen Loch” entfernen – nur, dass es irgendwann unter dem Einfluss der Gravitation umkehrt und wieder zurückfällt.
Zweiter wichtiger Unterschied ist, dass Körper immer dann aus dem Newtonschen Schwarzen Loch entkommen können, wenn sie beschleunigen. Sie müssen dabei nicht schneller werden als die Grenzgeschwindigkeit c=299.792.458 m/s, ja, sie müssen dieser Geschwindigkeit noch nicht einmal nahekommen. Sie müssen lediglich den durch die Gravitationskraft verursachten Geschwindigkeitsverlust ausgleichen. (Dass Lichtteilchen je nach ihrer Vorgeschichte viele verschiedene Geschwindigkeiten kleiner als c haben können, ist eine unschöne Komplikation des Newtonschen Modells.) Von solchen beschleunigten Körpern – Raketen mit Schub – ist ja im Text durchaus die Rede, nur dass der Leser den falschen Eindruck bekommen muss, auch sie kämen nicht vom Newtonschen Pseudo-Schwarzen Loch weg.
In der Allgemeinen Relativitätstheorie ist der Horizont dagegen tatsächlich eine Grenze: egal um was für ein Objekt es sich handelt, und egal wie es beschleunigt: wenn es einmal drinnen ist, kann es diese Grenze nie mehr überschreiten.
Zur Argumentation mit der Fluchtgeschwindigkeit selbst wird gesagt, die sei bei “größeren Körper[n]” größer. Wer da bei Größe direkt an die Ausdehnung oder das Volumen denkt (eben was man so allgemein unter Größe versteht), hat schon verloren, denn natürlich ist die Fluchtgeschwindigkeit bei gleicher Masse umso größer, je *kleiner* der betreffende Körper ist.
Zuletzt noch zum Licht: “Es versucht also zu dem massereichen Körper hinzufallen, doch weil es eben Licht ist und nicht eine wirkliche Masse wie Newtons Apfel, plumpst es nicht wirklich auf den Körper drauf, sondern wird nur ein wenig zu ihm gelenkt.” Ähem. Wie war das doch gleich mit der Universalität des freien Falls? Warum soll hier die Masse/nicht-Masse abgelenkter Licht- oder Materieteilchen eine Rolle spielen?
Das sind alles keine Nebensächlichkeiten, sondern die physikalischen Grundlagen. Verwirrung und Frustration warten dann leider ausgerechnet auf diejenigen Leser, die diese Grundlagen verstanden haben, daraus die richtigen Schlüsse ziehen, und dann an ihrem Verständnis zweifeln, weil in diesem Blogbeitrag etwas ganz anderes steht.
Niveauunterschiede im Unterrichten
Markus Pössel hat zwar Recht, dass die oben vorgestellte Beschreibung keine wissenschaftliche Berechnung von SLn ermöglicht. Das soll sie aber auch nicht, denn ein Neuntklässler kann noch keine Relativitätstheorie, weil der Mathematik-Unterricht ihm das Handwerkszeug noch nicht dazu gab. m.E. ist es dennoch wichtig und auf diesem Niveau bereits möglich, die Idee zu verstehen, worum es geht: Schwarze Löcher sind eben nicht das, wofür sie in der ScienceFiction oft hergenommen werden: niederträchtige Monster, die Menschen fressen.
Singularitäten zu verstehen oder Ereignishorizonte abzuleiten ist ein schwierigeres Terrain als es auf dem vorgestellten Schulniveau möglich ist. Man muss das natürlich andeuten, wenn man die obige heuristische Erklärung hernimmt, aber man kann es eben noch nicht exakt machen – man könnte auch interessierten Schülern die relativistische Rechnung zeigen, sodass Mathe-Talente das Thema autodidaktisch weiterstudieren können, aber fürs allgemeine Niveau ist die RT in der Mittelstufe wohl eher nicht geeignet.
Mit dem obigen Grundsatzverständnis nimmt man aber sogar einem Realschüler, der nach der 10 Klasse die Schule verlässt und einen Handwerksberuf lernt, die Angst vor dieser “kosmischen Bedrohung”, denn so werden diese Objekte verwaltbar und halbwegs einordenbar ins physikalische Weltbild. Es nimmt der Frage die Esotherik.
“Black Hole models”
Ich möchte auf eine Möglichkeit hinweisen, Schwarze Löcher im Rahmen der ART ein wenig verständlicher zu machen. Diese Idee ist schon recht alt und wurde (soweit mir bekannt ist) von William G. Unruh eingeführt und später von Andrew Hamilton ( http://arxiv.org/abs/gr-qc/0411060 ) zum sog. “River Model” ausgearbeitet. Die Gründzüge basieren
auf der Annahme, die Raumzeit verhalte sich wie eine Flüssigkeit mit einer konstanden Schallgeschwindigkeit (die der Lichtgeschwindigkeit entsprechen soll). Diese (Raumzeit) kann sich jedoch unter bestimmten Bedingungen mit Überschallgeschwindigkeit fortbewegen, so dass an der Stelle wo Fließ- und Schallgeschwindigkeit gleiche Werte einnehmen, sich ein Horizont bildet…
Zwar hat auch dieses Modell seine Schwächen (wachsende sprich dynamische Schwarze Löcher können nicht ausreichend gut beschrieben werden), aber es kann einem die fundamentalen Eigenschaften eines Horizontes vergegenwärtigen. Als Beispiel sei die Rotverschiebung und damit vebundene Zeitdilatation genannt, die zwar für einen externen Beobachter gegen unendlich divergieren, aber nicht das “tatsächliche Festfrieren des hereinfallenden Objektes” vor dem Horizont implizieren. Dieses hat den Horizont bereits in endlicher Zeit überschritten, da es ja mit der Raumzeit sich fortbewegte. Einzig die bei dem Einfall emittieren Schallphononen benötigen unendlich lange, um vom Horizont noch zu entkommen.
Dieses Modell ist verständlicher und physikalisch wesentlich näher an den Aussagen der ART als die Argumentationskette bezüglich der Fluchtgeschwindigkeit.
Trotzdem finde ich es sehr löblich, bereits jungen Schülern auch abstrakte Gebilde wie Schwarze Löcher zu erklären.
Re: Niveauunterschiede
Mir ist, wie könnte es anders sein, klar, dass man Mittelstufenschülern nicht mit der Mathematik der Allgemeinen Relativitätstheorie kommen sollte. Und ich finde es im Prinzip ebenfalls sehr löblich, Schülern schon in der Mittelstufe Informationen über spannende Themen wie Schwarze Löcher zu vermitteln, die dann natürlich auf dem Physikwissen der Mittelstufe aufbaut.
Aber was mich sehr stört ist, dass die Aussagekraft des vereinfachten Modells, die Eigenschaften der Fluchtgeschwindigkeit und der Zusammenhang zwischen Lichtablenkung und Masse in diesem Blogbeitrag falsch und/oder irreführend dargestellt werden. Und zwar gerade nicht in einer Weise, die sich mit dem Zwang zur einfachen Darstellung oder mit der Beschränkung auf Mittelstufen-Physik rechtfertigen liesse.
Es geht um die gewitzte Neuntklässlerin, die die Rechnung mit der Fluchtgeschwindigkeit ausführt und sich wundert, warum sich Licht und Teilchen in ihrer Rechnung sehr wohl weit von der Masse entfernen können, und warum sie keinen klar definierten “Ereignishorizont” ausmachen kann. Obwohl es sich im Blogtext so anhört, als sollte sie so etwas ableiten können. Die Lösung: gar nicht erst so tun, als gebe es im Newtonschen Modell so etwas wie einen Horizont. Stattdessen klar sagen: folgendes [folgt Beschreibung] ergibt sich aus den Betrachtungen zur Fluchtgeschwindigkeit; bei echten Schwarzen Löchern sind die Verhältnisse aber noch anders, nämlich [folgt einfache Prosabeschreibung ohne Formeln].
Es geht um den Neuntklässler, der die Formel für die Fluchtgeschwindigkeit sieht und verwirrt ist, weil im Blogbeitrag steht, größere Körper hätten eine größere Fluchtgeschwindigkeit – was nun einmal in der naheliegendsten Bedeutung, Größe gleich Ausdehnung oder Volumen, falsch ist.
Und es geht um die Neuntklässlerin, die die Universalität des freien Falls verstanden hat, und der im Blogtext fälschlicherweise suggeriert wird, irgendwie hinge es aber doch von der Masse ab, wie Materie einerseits und Licht andererseits fällt. Wo doch das Beispiel im Gegenteil die tolle Gelegenheit bietet, aus einfacher Schulphysik wie der Universalität des freien Falls etwas ganz Unerwartetes abzuleiten, nämlich (zumindest qualitativ) die Lichtablenkung.
@Michael: Ich bin ein grosser Freund des Fluss-Modells, das mir bislang aber nur in Prosa-Form begegnet war – danke für den Literaturhinweis!
Re: @ letzte beide Beiträge
1. Das Flussmodell schließt das Fluchtgeschwindigkeitsmodell nicht aus: Beide korrellieren sogar eng miteinander, wie man dem verlinkten Artikel entnehmen kann. Herzlichen Dank für diesen Beitrag!
2. Das Fluchtgeschwindigkeitsmodell erklärt sehr gut, warum diese Objekte schwarz sind. Und weshalb sie als “Löcher” bezeichnet werden, die sich aber von Gullilöchern einer Straße unterscheiden, obwohl sie mit ihnen etwas gemein haben: nämlich dass sie aus der Ferne keine Gefahr bilden.
Sogar ein Horizont ist m.E. sehr klar kommuniziert in diesem stark vereinfachten Modell, denn ein Horizont im umgangssprachlichen Sinn, also eine Art Grenze, hinter die man nicht schauen kann (http://de.wikipedia.org/wiki/Horizont), hat bisher jede/r durch die Tatsache verstanden, dass es keinen “Boten” gibt, da das Licht von dieser Grenze nicht wegkommt.
3. Den empfohlenen Satz “bei echten Schwarzen Löchern sind die Verhältnisse aber noch anders” habe ich geschrieben, nur anders ausgedrückt, und bisher stets kommuniziert. Danke aber nochmals für diesen wichtigen Hinweis! Es darf wirklich auf keinen Fall vergessen werden.
4. Es gibt in der Wissenschaft (und ihrer Didaktik) _immer_ mehrere Modelle: Das ist eben der Charakter von Modellen, dass sie ja nur Versuche sind, Abstrakta in unsere Realität abzubilden. Für diese Abbildungen gibt es immer verschiedene Projektoren, die entweder Gleiches auf verschiedene Weise ausdrücken (so wie synonyme Vokabeln) oder ein Phänomen verschieden tief beleuchten – so wie in diesem Fall der Modelle vom Fluss und von der Fluchtgeschwindigkeit. Letzteres ist viel oberflächlicher und tangiert die Raumzeitstruktur mitnichten. Es schöpft sich rein aus den “Erfahrungswerten” menschlicher Ingenieurskunst (Astronauten auf dem Mond).
Das Flussmodell ist zwar auch hübsch und in manchen höheren Schulklassen brauchbar, aber die meisten Menschen denken Gravitation nicht in Potentialtöpfen wie wir es in der Physik tun – eine wichtige Visualisierung für das Flussmodell der Raumzeit.
In der Öffentlichkeit (oder Mittelstufe) hat man Glück, wenn sogar Physik-Desinteressierte wissen, dass man vom Mond eine andere Fluchtgeschwindigkeit hat als von der Erde. Darum zeigt meine Erfahrung, dass man sie damit besser abholt als mit Beschreibungen der Raumzeit, die man erst vorbereiten müsste. In einem öffentlichen Vortrag kann man das natürlich tun – oder eben in höheren Schulklassen, aber die Frage ist ja immer: wieviel Platz (Zeit) haben solche Themen denn überhaupt in unserem Schul- oder Publikationsalltag?
Exkurs für Herrn Pössel:
“Größe” ist ein schwieriger Begriff, der immer erst aus dem Kontext klar wird: bei Gravitationslinsen bezieht er sich immer auf Massen, umgangssprachlich oft auf räumlich Ausdehnung oder Höhe (bei Personen), bei Menschen u.U. auf deren Würde oder Virtuosität (Victoria war eine große Königin, Einstein war ein großer Wissenschaftler, wenngleich nicht gerade hoch). Hinsichtlich der Fluchtgeschwindigkeiten gehen hier (wie man in der Formel leicht sieht) eben nicht nur Masse, sondern auch Volumen des Himmelskörpers ein.
PS: Beim Erklären auf dem Niveau der neunten Klasse holt man nicht nur SchülerInnen ab: Es ist das, auf dem man auch bei öffentlichen Sternwartenbesuchen u.ä. einsteigt und mithin auch für erklärende Hobby-AstronomInnen interessante Modelle liefert. Auf diesem Niveau geht es – wie gesagt – tatsächlich nicht um eine mathematische, sondern rein heuristische Beschreibung, d.h. man kann lediglich die Idee skizzieren.
Ich danke unter diesen Gesichtspunkten den Kollegen für das Kompliment “löblich”, finde es aber eigentlich sogar _elementar_, diese populistische und populärwissenschaftliche Frage auf möglichst niedrigem Niveau zu diskutieren und d.h. m.E. ohne Raumzeitgeometrien. Neugierige werden selbstverständlich bei der Vertiefung dieses (auch für meine persönlichen Ansprüche viel zu oberflächlichen Sichtweise) Themas schnell auf andere Modelle und bald auf viel faszinierende Mathematik als nur eine simple Wurzel stoßen – aber das ist ja auch gerade das Schöne an der Forschung. 🙂 ne?!
Fluss vs. Fluchtgeschwindigkeit
Klar gibt es oft mehrere Modelle, um einen bestimmten physikalischen Sachverhalt vereinfacht darzustellen. Trotzdem muss man fragen, wie gut ein bestimmtes Modell ist, wo es Schwaechen hat, und ob die Schwaechen vielleicht so gross sind, dass man das Modell fallen lassen sollte.
Beim Fluchtgeschwindigkeitsmodell bin ich inzwischen der Meinung, dass es mehr schadet als nuetzt.
Dass das Fluchtgeschwindigkeitsmodell und das Flussmodell “eng korrelieren” halte ich fuer eine sehr gewagte Behauptung. Klar kommt die Fluchtgeschwindigkeit in den Formeln vor – wie sollte es anders sein, so wenige dimensionsbehaftete Groessen, wie im Spiel sind? – aber die Mechanismen und Aussagen sind eben verwirrenderweise grundverschieden.
Zum “Horizont” – Licht kommt bei Newton vom Schwarzschildradius eben sehr wohl “weg”. Licht erreicht beliebig grosze, obschon endliche Entfernungen vom angeblich so schwarzen Newtonschen Loch. Ddas Flussmodell gibt die Eigenschaften relativistischer Schwarzer Loecher hier richtig wieder, das Fluchtgeschwindigkeitsmodell nicht.
Gaenzlich erstaunlich finde ich die Aussage, das Flussmodell sei vielleicht in manchen hoeheren Schulklassen brauchbar, aber für Mittelstufe und Oeffentlichkeit irgendwie zu anspruchsvoll. Es geht um einen Fluss, mit Fischen – das ist doch eigentlich deutlich naeher an der direkten Erfahrung als der indirekte Bezug zu den Astronauten, die mit (beschleunigten!) Raketen auf den Mond geflogen sind? Sogar die Mathematik ist einfacher. Wo brauchte man da, solange es nur um das Modell selbst und nicht den Unterbau geht, Potentialtoepfe oder “Beschreibungen der Raumzeit, die man erst vorbereiten muesste”?
Zu dem an mich gerichteten Exkurs: In dem gegebenen Zusammenhang gibt es ziemlich genau zwei Moeglichkeiten, was mit “Groesze” gemeint sein kann: Masse oder (lineare/raeumliche) Ausdehnung. Und bei der meiner Einschaetzung nach naheliegenderen der beiden moeglichen Bedeutungen (Ausdehnung) ist die getroffene Aussage falsch. Solche potentiellen Missverstaendnisse sollte man moeglichst vermeiden.
Schwarze Löcher
Guten Tag, Frau Hoffmann
Hab gerade die 1/2009 SUW in die Finger bekommen und nutze die Gelegenheit, die angeboten wird:
Mein Freund, Mathematiker, versucht mir einzureden, S.L. seien Singularitäten. Er hat aber keine Argumente für diese Behauptung. Singularitäten gibt es m.A. nur in der Mathematik. Ich erbitte Ihre Meinung. Danke! MfG.
P.S. Die ersten Zeilen Ihrer Erklärung im Blog sind etwas durcheinander geraten. Schon gemerkt? ggf. Korrektur
Ja, Schwarze Löcher sind mathematisch beschreibbar als Singularitäten der Raumzeit. Wissen Sie eigentlich, warum man bei Aristoteles die Welt als zweigeteilt beschrieben findet: Es gibt einen irdischen und einen himmlischen Bereich, weil auf der Erde alles scheinbar anders funktioniert als am Himmel. In Worten der modernen Physik: Es gibt am Himmel weniger störeinflüsse als auf der Erde. Luft und andere Reibung z.B. fehlt und Singularitäten können eben doch auftreten. Das ist doch gerade das großartige an der Astronomie: Wir können hier oft direkt nachschauen, ob die Mathematik, die wir in der Physik benutzen, tatsächlich funktioniert. Ich meine, das Buch der Natur ist u.a. auch in mathematischen Lettern schreibbar – die Natur schreibt es selbst zwar in anderen Bildern, aber wir übersetzen es in Mathematik. In der Realität ist das zwar oft unvollständig, aber es gibt doch Störungsrechnungen etc. …
Man sollte aber auf Schulniveau m.E. nicht mit den Mitteln der Analysis arbeiten, die man erst nach dem Mathe-Vordiplom hat. Um mit einem vierdimensionalen Raumzeitvektor umzugehen, fällt vielen Schülern ebenso schwer wie mit gewöhnlichen Differentialgleichungen zweiter Ordnung – und seien es nur simple Integrale der e-Funktion, die auch erst in den höheren Gymnasialklassen drankommen.
Die Tolman-Oppenheimer-Volkoff-Gleichung und das Birkhoff-Theorem für sphärisch symmetrische Materieverteilungen arbeiten mit Energie-Impulstensoren, wovon Schüler fast nie was hören.
Will man sogar Quantengravitation einführen, dann muss man vielleicht noch die Poisson-Algebra einführen. (also, ich würde das tun – weiß nicht, ob man muss, halte ich aber für schulisch einfachstens)
Soweit mir bekannt ist, ist für all sowas in der Schule keine Zeit. Schule soll ja auch Allgemeinbildung vermitteln, nicht bereits ein Physikstudium. Wer das haben will, macht es gewöhnlich anschließend, nach dem Abitur.
Da also die allgemeinbildende Schule in puncto Schw. Löcher und wohl auch allg. der Naturwissenschaft auf einem recht heuristischen Niveau bleibt, sollte an dieser Stelle die oben beschriebene “visuelle” Erklärung hinreichen. So könnte sich also auch jemand, der hinterher vielleicht nicht Physik studiert, sondern Künstler wird und tolle Kinofilme macht, merken, dass Schw Löcher keine Apokalypse sind, sondern ein sehr interessantes Naturphänomen.
Oder: Wieviele Menschen haben in der Schule gelernt und verstanden, was überhaupt eine Singularität ist?
Schwarze Löcher
Schwarzer Stern wäre ein treffenderer Begriff, denn es handelt sich ja um den stark verdichteten Überrest eines ehemals hell leuchtenden Sterns. Schwarze Sterne sind die am dichtesten zusammengedrückte Materie im Universum. Sie beeinflussen nicht nur Materie, Licht und den Raum, sondern auch die Zeit.
Es ließe sich vieles Interessantes über Schwarze “Löcher” berichten, und so ganz nebenbei Interesse für andere Gebiete der Astronomie wecken.
Danke
Ein sehr schöner Artikel, gut zusammengefast, geht aber nicht ZU sehr ins Detail, sehr gut. Soll ja nicht jeder Astrophysiker werden, aber eine generelle Allgemeinbildung mehr in diesem Themenbereich fände ich persönlich anstrebenswert. Besonders, da dieser Bereich in Zukunft unser Leben mehr und mehr beeinflussen wird.