Gravitationswellenquellen (GW Teil 3)
BLOG: RELATIV EINFACH

Der Donnerstag, der uns wahrscheinlich die Bekanntgabe des ersten direkten Nachweises von Gravitationswellen bescheren wird, rückt näher. Und wie immer gilt: Wer schon etwas weiß, hat mehr von solchen Nachrichten. Daher meine Kurzserie zu Gravitationswellen.
In Teil 1 hatten wir erkundet, was Gravitationswellen sind und wie sie wirken, in Teil 2 wie man sie nachweisen kann. Aber wie entstehen Gravitationswellen?
Gravitations-Sendeantennen
Die einfachste Situation, in der Gravitationswellen entstehen, kommt im Weltraum sehr häufig vor. Man benötigt lediglich Objekte, die sich (in der Regel zusammengehalten durch ihre gegenseitige Schwereanziehung) umkreisen. Die Art und Weise, wie sich die Verzerrungen rund um die Masse im Raum ausbreiten erinnert an Wasser rund um einen langsamen Quirl. Hier ist eine Visualisierung, die mir Sascha Husa von der Universitat de les Illes Balears freundlicherweise zur Verfügung gestellt hat: 
Dargestellt sind die Verzerrungen in der Ebene, in der die beiden Körper sich umkreisen (das Umkreisen kann man erahnen, ganz klein in der Mitte). Die Höhe der dargestellten Welle gibt die Verzerrung wieder (vereinfacht: Streckung bzw. Stauchung in eine der Richtungen senkrecht dazu; genauer: Realteil vom Strain).
Ein indirekter Nachweis
Gravitationswellen transportieren Energie. Die geht dem System verloren, das die Gravitationswellen aussendet. Aus der Allgemeinen Relativitätstheorie folgt eine Näherungsformel für das Ausmaß des Energieverlusts, in Abhängigkeit von den Massen der Objekte und ihrer Umlaufzeit umeinander.[1]
Was passiert, wenn man einem System einander umkreisender Körper fortwährend Energie entzieht, lässt sich bereits auf dem Niveau der Schulphysik verstehen (Kepler lässt grüßen): die Körper rücken näher aneinander und umkreisen sich zunehmend schneller.
Anhand solch einer gravitationswellenbedingten Abnahme der Umlaufzeit eines Doppelsystems aus zwei Neutronensternen gelang der erste indirekte Nachweis von Gravitationswellen (die Entdeckung wird beschrieben in Hulse & Taylor 1974, der indirekte Nachweis nach sieben Jahren Auswertung der Umlaufzeiten in Taylor & Weisberg 1984). Die Übereinstimmung mit der Vorhersage der Quadrupolformel für den Zusammenhang von Umlaufzeitänderung, Massen, Umlaufzeit und Bahnradius war bereits damals so überzeugend, dass Hulse und Taylor für diesen Nachweis 1993 den Physik-Nobelpreis bekamen.
Die folgende Abbildung aus Weisberg 2010 zeigt diese Übereinstimmung für alle Messungen bis einschließlich 2005:
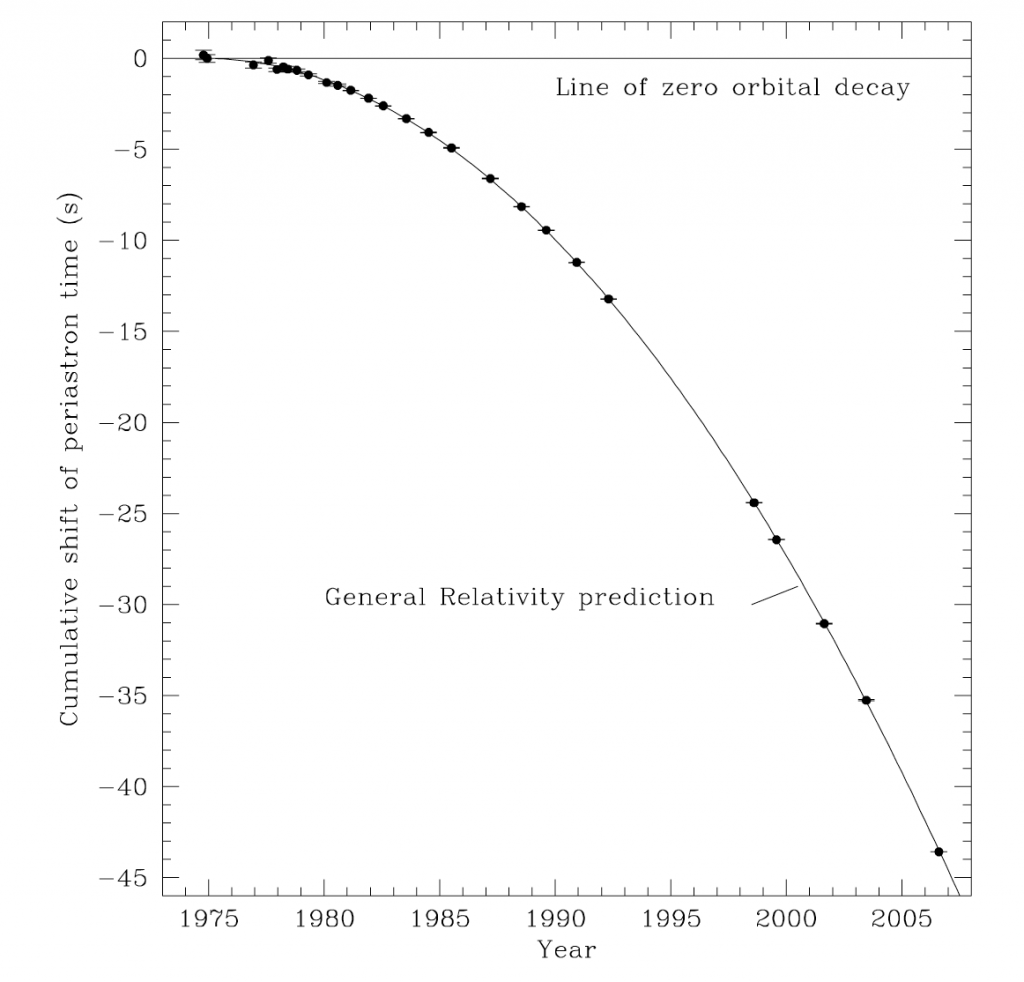 Auf der x-Achse ist dabei das Jahr aufgetragen, in dem gemessen wurde. Auf der y-Achse ist aufgetragen, um wieviel eher als ohne Gravitationswellenabstrahlung erwartet die beiden Neutronensterne damals den Bahnpunkt größter gegenseitiger Annäherung durchliefen. Die Fehlerbalken für die Messungen sind so kurz, dass sie in der Abbildung zumeist wie ein einziger Mittel-Querschnitt durch den Datenpunkt aussehen. Die Übereinstimmung zwischen den Datenpunkten und der Vorhersage der Allgemeinen Relativitätstheorie (durchgezogene Kurve) ist beachtlich.
Auf der x-Achse ist dabei das Jahr aufgetragen, in dem gemessen wurde. Auf der y-Achse ist aufgetragen, um wieviel eher als ohne Gravitationswellenabstrahlung erwartet die beiden Neutronensterne damals den Bahnpunkt größter gegenseitiger Annäherung durchliefen. Die Fehlerbalken für die Messungen sind so kurz, dass sie in der Abbildung zumeist wie ein einziger Mittel-Querschnitt durch den Datenpunkt aussehen. Die Übereinstimmung zwischen den Datenpunkten und der Vorhersage der Allgemeinen Relativitätstheorie (durchgezogene Kurve) ist beachtlich.
Frequenz als Ausschlusskriterium
Für bei weitem nicht alle der sich umkreisenden Systeme können die heutigen interferometrischen Gravitationswellendetektoren die Gravitationswellen dann auch wirklich nachweisen.
Ein wichtiges Kriterium ist der Frequenzbereich der betreffenden Signale. Die bodengebundenen Detektoren sind nur bei Frequenzen höher als 10-100 Hz empfindlich genug (10-100 Schwingungen pro Sekunde; die untere Region erreicht meines Wissens nach nur der VIRGO-Detektor). Bei niedrigeren Frequenzen sind seismische Störungen zu stark, also die immer präsenten leichten Schwankungen des Erdbodens. Trotz aufwändiger Gegenmaßnahmen überträgt sich von diesen Schwankungen genug auf den Detektor überträgt (zum Teil sogar vermittels der Gravitation der beteiligten Massen!), um Nachweise bei niedrigeren Frequenzen praktisch unmöglich zu machen.
Der Nachweis der Gravitationswellen supermassereicher Schwarzer Löcher oder weiße Zwerge wird sich gedulden müssen, bis weltraumgestützte Gravitationswellendetektoren einsatzbereit sind. Der Nachweis so langsamer (weil relativ weit voneinander entfernter) Neutronensternpaare wie dem Hulse-Taylor-Pulsar auch – allenfalls eine Langzeitanalyse nach solch einem (fast) periodischen Signal könnte da weiterhelfen, aber auch solche Analysen hatten bislang keinen Erfolg.
Gravitations-Zirpen
Wahrscheinlichster Nachweiskandidat ist dagegen eine andere Art von Signal namens “Zirpen” (im Original: chirp).
Je kürzer die Umlaufzeit sich unter der eigenen Schwerkraft umkreisender Körper, umso größer die Energie, die das System abstrahlt. Je mehr Energie das System abstrahlt, umso rascher nimmt die Umlaufzeit ab. So schaukelt sich die Gravitationswellenabstrahlung auf, bis die sich umkreisenden Objekte schließlich zusammenstoßen und das Umkreisen aufhört.
Das Ergebnis ist ein Zirpen, bei dem die Umlauffrequenz und damit die Frequenz der Gravitationswelle immer höher, die Intensität der Welle immer größer werden. So sieht der Verlauf aus (Abbildung und Tondateien entnommen aus Das Zirpen der Neutronensterne auf Einstein Online):
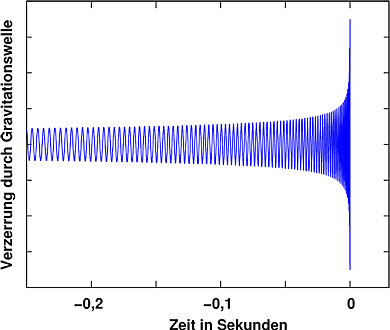 Wie es sich so trifft, liegen die Frequenzen, um die es da geht, für stellare Schwarze Löcher und/oder Neutronensterne gerade im hörbaren Bereich. Zur Veranschaulichung kann man daher einen Ton erzeugen, der genau den gleichen Frequenzverlauf hat und auch in ähnlicher Weise lauter wird, wie die Intensität der Wellen anwächst (Audio © B. Owen, Penn State University):
Wie es sich so trifft, liegen die Frequenzen, um die es da geht, für stellare Schwarze Löcher und/oder Neutronensterne gerade im hörbaren Bereich. Zur Veranschaulichung kann man daher einen Ton erzeugen, der genau den gleichen Frequenzverlauf hat und auch in ähnlicher Weise lauter wird, wie die Intensität der Wellen anwächst (Audio © B. Owen, Penn State University):
Hier ist das gleiche nochmal für die Verschmelzung von Schwarzem Loch und Neutronenstern (© AEI/GEO600)
Und hier noch einmal mit Störquellen überlagert, wie es in einem echten Detektor der Fall wäre (© AEI/GEO600)
Die Kollegen in Cardiff haben daraus das Online-Spiel Black Hole Hunter gemacht, bei dem man versuchen kann, Chirp-Signale aus dem Hintergrundrauschen herauszulauschen.
Solche Chirps, und zwar für Neutronensterne und stellare Schwarze Löcher (sprich: Schwarze Löcher mit einigen bis einigen Dutzend Sonnenmassen) sind die wohl besten Kandidaten für Gravitationswellensignale, die für die heutigen Gravitationswellendetektoren im Prinzip nachweisbar sind.
Die Verschmelzungsphase ganz am Ende ist dann nicht mehr durch einfache Formeln zu beschreiben, sondern Zuständigkeitsgebiet der numerischen Relativitätstheorie, die diese und andere relativistische Vorgänge im Computer simuliert.
Das große Warten
Morgen ist es vorbei, das große Warten. Dann dürften wir wissen, dass die Gravitationswellendetektoren aLIGO etwas gesehen haben, und was. Die Gerüchte sprechen in der Tat von einem “Chirp”, bei dem zwei nicht allzu leichte Schwarze Löcher verschmolzen sind.
Bis zum Nachweis konnten die Gravitationswellenforscher allenfalls Abschätzungen liefern, wieviele Ereignisse sie mit ihren Detektoren voraussichtlich pro Jahr würden nachweisen können.
Allgemein gilt, dass Gravitationswellensignale mit der Entfernung der Quelle schwächer werden. Aus der Empfindlichkeit des Detektors ergibt sich, bis in wie große Entfernung der Detektor eine bestimmte Quelle gerade noch nachweisen kann. Dafür, wann und wo Schwarze Löcher und/oder Neutronensterne verschmelzen, lassen sich keine konkreten Vorhersagen treffen. Man kann nur versuchen, abzuschätzen, wie oft solche Ereignisse in einer gegebenen Raumregion (sprich: in einem gegebenen Volumen) vorkommen. Die Empfindlichkeit des Detektors bestimmt das Volumen, innerhalb dessen er ein bestimmtes Ereignis nachweisen kann. Insgesamt ergibt sich so eine Abschätzung der Nachweiswahrscheinlichkeit.
Am besten geht das bei der Verschmelzung zweier Neutronensterne, denn für Neutronensterne weiß man genauer, unter welchen Bedingungen sie entstehen und wie häufig das vermutlich vorkommt. Hier eine Tabelle der jüngsten Abschätzungen, erstellt von der LIGO Scientific Collaboration 2013:
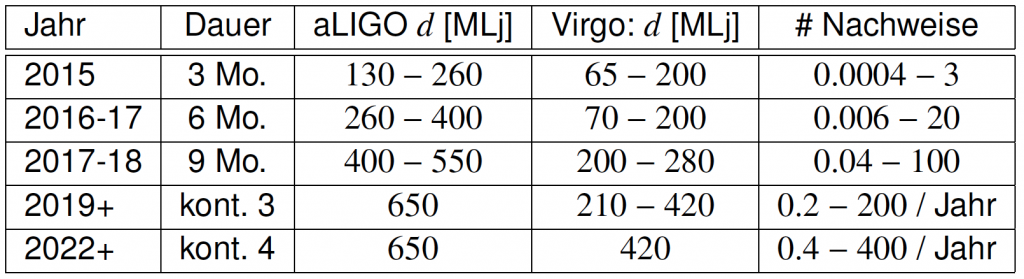 Angegeben sind die Abschätzungen für jedes Jahr; Ausgangspunkt ist die Planung, wieviele Detektoren mit welchen Empfindlichkeiten in dem betreffenden Zeitraum in Betrieb sein werden. “Dauer” sagt aus, wie lange die Detektoren in dem Jahr pro Jahr in Betrieb sein werden, “kont. 3” ist kontinuierlicher Betrieb mit 3 Detektoren. Dann ist für aLIGO (die Advanced LIGO-Detektoren, derzeit 2 in den USA, später soll einer in Indien dazukommen) und Virgo (in Italien) angegeben, bis zu welcher Entfernung sie verschmelzende Neutronensterne nachweisen könnten.
Angegeben sind die Abschätzungen für jedes Jahr; Ausgangspunkt ist die Planung, wieviele Detektoren mit welchen Empfindlichkeiten in dem betreffenden Zeitraum in Betrieb sein werden. “Dauer” sagt aus, wie lange die Detektoren in dem Jahr pro Jahr in Betrieb sein werden, “kont. 3” ist kontinuierlicher Betrieb mit 3 Detektoren. Dann ist für aLIGO (die Advanced LIGO-Detektoren, derzeit 2 in den USA, später soll einer in Indien dazukommen) und Virgo (in Italien) angegeben, bis zu welcher Entfernung sie verschmelzende Neutronensterne nachweisen könnten.
Die Zahlenwerte hängen von einer Reihe von Annahmen ab, für die es pessimistischere und optimistischere Versionen gibt. Entsprechend variiert auch die Anzahl der im betreffenden Jahr zu erwartenden Nachweise einer Neutronenstern-Verschmelzung, Spalte ganz rechts.
Eine neue Abschätzung ist übrigens gerade vor ein paar Tagen auf Living Reviews in Relativity erschienen.
Für Schwarze Löcher sind die Häufigkeiten deutlich unsicherer. Aber da kann man dann ja hoffentlich ab Donnerstag auf erste empirische Daten zurückgreifen.
Was noch außer Chirps?
Was kann man sich außer den Chirps verschmelzender Neutronensterne oder Schwarzer Löcher noch erhoffen?
Da wären zum einen kontinuierliche Signale, wie sie zum Beispiel entstehen würden, wenn ein rasch rotierender Neutronenstern einen winzigen Buckel hätte. Nach solchen Signalen sucht man schon recht lange. Neutronensterne scheinen aber sehr, sehr glatt zu sein. Schade. Bislang nichts gefunden.
Dann kommen diejenigen Signale, die man weniger gut versteht, weil die Physik dahinter komplizierter ist. Supernova-Explosionen sind das beste Beispiel, denn auch dort kann der Kollaps der Zentralregionen zu einem Neutronenstern Gravitationswellen erzeugen – deren Stärke allerdings sehr davon abhängt, was da im Einzelnen passiert und wie asymmetrisch der Kollaps ist. Mit solchen Themen beschäftigen sich z.B. Kollegen am Max-Planck-Institut für Astrophysik in Garching.
Und dann wären da natürlich noch die Signale, die niemand erwartet. Bislang hat es in der Astronomie jedesmal Überraschungen gegeben, wenn ein neuer Typ Informationsträger zugänglich wurde – man denke z.B. an die Quasare und Radiogalaxien, mit denen niemand gerechnet hatten, bevor die Radioastronomie begann und diese Objekte entdeckt wurde. Was wartet da draußen wohl noch auf uns?
[1] Die Hintergründe dieser Rechnung sind alles andere als ohne – man kommt zu der Formel zwar recht einfach, aber es ist gar nicht so einfach die dabei gemachten Annahmen richtig zu begründen. Insbesondere das Zusammenspiel der verschiedenen Näherungen, die man dabei vornimmt, hat die Physiker bis in die 1980er Jahre kontrovers diskutieren lassen; Details finden sich in dem in Teil 1 bereits erwähnten Buch “Traveling at the Speed of Thought” von Daniel Kennefick und in diesem Artikel desselben Autors.


Hallo Markus,
danke für die schöne Serie zu Gravitationswellen. Da ist man ja wirklich gut gewappnet für die Pressekonferenz heute Nachmittag.
Schon öfter habe ich gehört, dass die Amplitude von Gravitationswellen nur linear mit dem Abstand von der Quelle abnimmt und man daher mit zehn mal empfindlicheren Detektoren 1000x mehr Volumen erhält, ein nicht zu vernachlässigender Vorteil dieses Fensters ins All. In der Grafik von Sascha Husa oben sieht es auch so aus, als ob die Amplitude konstant bliebe. Ist dem wirklich so? Und wenn ja, wie verhält es sich mit der Energieerhaltung…?
Danke für eine Experten-Antwort!
Leo
Hallo Markus,
entschuldige bitte, dass ich mir selbst die Antwort gebe, aber ich habe sie nun in der Veröffentlichtung von gestern gefunden: Natürlich nimmt die Intensität von Gravitationswellen mit dem Abstand von der Quelle wie 1/r^2 ab, ansonsten wäre ja eben die Energie der Gravitationswelle nicht erhalten. Gravitationswellen-Interferometer messen aber nicht die Intensität, sondern die Amplitude der Welle und die nimmt bekanntermaßen nur mit 1/r ab, d.h. (im lokalen Universum) nimmt das Detektionsvolumen von LIGO tatsächlich ums tausendfache zu, wenn die Empfindlichkeit um das zehnfache gesteigert wird.
Danke für die Reihe.
P.s. die Fußnote ist noch nicht vernünftigt verlinkt.
Danke, ist jetzt korrigiert!
Können Gravitationswellen – ähnlich wie Licht – in Gravitationsfeldern großer Massen abgelenkt werden?
Ja, solche Effekte gibt es. Auch Gravitationswellen werden dadurch beeinflusst, auf welchem Hintergrund (z.B. durch Massen gekrümmte Raumzeit) sie sich fortbewegen.
Zukünftige weltraumbasierte Graviationswellensensoren sollen gemäss Studying Inflation with Future Space-Based Gravitational Wave Detectors sogar die Inflationsphase untersuchen können. DECIGO .- ein zukünftiges japanisches weltraumbasiertes Gravitationswellendetektor System, das im DeziHertz-Frequenbereich arbeitet – soll die inflationären Gravitationswellen nachweisen können.
In weiter Ferne ist da noch vieles spannende. Florian Freistetter hat hier eine schöne Schilderung: http://scienceblogs.de/astrodicticum-simplex/2016/02/11/was-koennen-und-wozu-braucht-man-gravitationswellen/ – und ich habe hier noch nachgelegt: https://scilogs.spektrum.de/relativ-einfach/gravitationswellen-warum-die-aufregung/
Was mich auch interessiert: Wie groß ist das Potential der Untersuchung von Dunkler Materie mittels Gravitationswellen? Ich fand da 1-2 Paper dazu, aber gewann da keinen rechten Überblick.
Eher wenig. Da Dunkle Materie außer über die Gravitation nicht mit anderer Dunkler Materie wechselwirkt, bleibt sie ein diffuser Halo. Kompakte, sich umkreisende Objekte, also gute Gravitationswellenquellen, bekommt man auf diese Weise nicht.
Ausnahme, soweit ich weiß: Weltraumgestützte Detektoren haben als Hoffnung, Dichteschwankungen der dunklen Materie in der Frühzeit des Universums nachzuweisen. Aber das ist alles entfernte Zukunftsmusik.
Markus Pössel schrieb (10. Februar 2016:
> […] Objekte, die sich (in der Regel zusammengehalten durch ihre gegenseitige Schwereanziehung) umkreisen. […]
> Hier ist eine Visualisierung, […] Sascha Husa von der Universitat de les Illes Balears
> [ https://scilogs.spektrum.de/relativ-einfach/wp-content/blogs.dir/210/files/quadrupol3.gif ]
> Dargestellt sind die Verzerrungen in der Ebene, in der die beiden Körper sich umkreisen (das Umkreisen kann man erahnen, ganz klein in der Mitte).
Abbildungen (Projektionen) von zwei (vermeintlich etwa kugelförmigen) Körpern, die um das Zentrum der Darstellung kreisen, habe ich da leider nicht erahnen können; so sehr ich auch versucht habe, mir die Umgebung der “Mitte” (zu der hin die Amplitudenberge in der Darstellung steil abfallen) genau anzusehen.
Aber vielleicht kann man sich solche Körper ja geeignet dazudenken.
Und wo genau sollte man sich denn diese beiden Körper hindenken, insbesondere in Bezug auf diese auffallend steilen Flanken der beiden Amplitudenberge, im Bereich der “Mitte“:
– jeweils eines genau vor einer dieser beiden Flanken(natürlich mitrotierend)?
– oder jeweils etwas phasenversetzt (und natürlich mitrotierend) gegenüber den Flanken?
Falls so: versetzt um welchen Phasenwinkel?
Wissenschaftlicher Humbug!
Wie den Medien zu entnehmen war, wollen die amerikanischen Physiker mit ihrem Observatorium zum Nachweis von Gravitationswellen angeblich die Längenänderung von einem Tausendstel des Durchmessers eines Wasserstoffatomkerns gemessen haben. Dies ist zurzeit absolut unmöglich! Denn der Durchmesser eines Wasserstoffprotons beträgt DH2p= 2,8*10-15 m. Ein Tausendstel davon wären nach Adam Ries dann 2,8*10-18 m. Übrigens erzeugt jede natürliche Erschütterung (vorbeifahrendes Auto, ja ein Fußgänger) in der Umgebung des Observatoriums eine bedeutend größere Erschütterung und Abweichung, wie die angeblich gemessene Längendifferenz von ∆s=2,8*10-18 m. Unabhängig davon, beträgt die maximale Auflösung von Licht allgemein 0,5 der Wellenlänge oder ∆x= λ/2. Für moderne Laser wird neuerdings eine maximale Auflösung von ∆x =10-² der Wellenlänge λ angegeben. Da vom Laser des amerikanischen Observatoriums zur Detektion von Gravitationswellen nicht der Wellenbereich angegeben wurde, soll das gesamte Spektrum für die Berechnung des Auflösungsvermögens betrachtet werden. Das sichtbare Spektrum der Wellenlängen reicht von ca. 390 nm (Nanometer – ein Milliardstel Meter) bis ca. 780 nm. Die Spannweite des Auflösungsvermögens bewegt sich also von 3,9 nm bis 7,8 nm. Dies sind 3,9 *10-9 bis 7,8*10-9 m. Das Auflösungsvermögen von Laserlicht liegt also um rund 9 Potenzen unter dem erforderlichen Auflösungsvermögen von 2,8 *10-18 m. Nun könnten die amerikanischen Forscher ganz clever gewesen sein und die Laufzeitdifferenz gemessen haben. Da ergibt eine noch katastrophalere Bilanz! Die Laufzeitdifferenz ∆t beträgt nämlich zirka 10-26 s. Denn:
∆t= ∆s:c= 2,8*10-18 m: 3*108 m/s ≈ 10-26s. (1)
Das Auflösungsvermögen von optischen Atomuhren beträgt gegenwärtig 10-17 s und liegt damit deutlich unter dem hypothetisch berechneten Auflösungsvermögen. Und bei der Betrachtung der Energiebilanz wird deutlich, dass aus einer Entfernung von
s= t*c=1,3 *109*365*24*3600 s* 300.000 km/s ≈ 1,3*109*3,2 *107*3*105 km ≈
1,2*1022 km (2)
von der Energie der drei Sonnen mit der Energie
ESL=m*c²= 3*2*1030 kg* 9*1016 m²/s² ≈ 5,4*1047 J (Joule) (3)
nur noch rund
EE=5,4*10 7 J=5,4*104 kJ ≈ 1,3 *104 kcal=13.000 kcal =1,5 kWh (4)
auf die Erdatmosphäre auftreffen und dann von ihr mit Sicherheit total absorbiert würden. Denn es gilt
EE= ESL: [(25*ASL:AE)* (R²:RE²]. (5)
weil die Energiedichte mit dem Quadrat der Entfernung vom Fusionsort der beiden schwarzen Löcher mit einer Gesamtmasse von 29+36=125 Sonnenmassen abnimmt und sich im Raum homogen verteilt. Anderseits bildet die Erde in Relation zu den beiden schwarzen Löchern nur eine ganz geringe Fläche, wobei sich das Verhältnis der beiden Flächen von den schwarzen Löchern mit dem Radius rSL und der Erde mit dem Radius rE allgemein wie folgt errechnet:
n=³√(125)²rSL²: rE². (6)
Damit ergibt sich eine Energie von
E= 5,4*1047 J: [(25*0,5*1012): (41*106)]*[1,44*1044: 0,5*1012] ≈
5,4*107 J=5,44*104 kJ=1,5 kWh. (7)
(Energieäquivalent einer Herdplatte von 1,5 kW Leistung für eine Stunde in Betrieb). Nach einem anderen Modell wird wohl streng genommen nicht ein J auf der Erde ankommen können, weil das All vom kosmischen Staub und den Planeten völlig dicht sein muss, auf einer Entfernung von E=1,2*1022 km. Und dies ist nun fast mehr als Nichts, einmal ganz salopp formuliert! Die Amerikaner sind wohl irgendwie auf Dummenfang gegangen, um an Forschungsgelder und an den Nobelpreis ranzukommen.
Siegfried Marquardt, Königs Wusterhausen
Advanced LIGO erreicht eine Auflösung von 10^-22 Meter in bestimmten Wellenlängebereichen (Frequenzen zwischen 100 und 10’000 Herz) weil
1) die Interferometrie den Phasenunterschied zweier Lichtstrahlen misst womit sich schon Laufdistanzunterschiede von Bruchteilen der verwendeten Laserwellenlänge bemerkbar machen
2) Die stärksten seismischen Störungen nicht im untersuchten Frequenzbereich liegen
3) Laserstrahlen die Weglänge nicht nur einmal sondern 10 Mal ablaufen bevor die Interferenz der beiden Strahlen bestimmt wird
4) Die Spiegel so gelagert sind, dass seismische Störungen kompensiert werden.
Siehe dazu auch die Wikipedia
Erdbebenwellen haben typischerweise Frequenzen unter 10 Hertz, was übrigens – wie das Bild hier zeigt – auch unter den Hörfrequenzen und der Frequenz menschlicher Sprache liegt.
LIGO hat seinen empfindlichen Bereich gerade im Hörfrequenzbereich. Ein Ligo-Chirp kann also frequenzmässig fast 1:1 in einen hörbaren Sound umgewandelt werden.