Was sind eigentlich Gravitationswellen? (GW Teil 1)
BLOG: RELATIV EINFACH

Die Gerüchte, dass wir am 11. Februar mehr über Gravitationswellen lernen, verdichten sich. Warum es immer noch “Alles nur eine Übung!” heißen könnte, hatte ich hier in “Gravitationswellen-Gerüchteküche” geschrieben. Aber vielleicht sind wir ja jetzt sogar schon in der Phase, wo zumindest den Beteiligten klar ist, ob es sich um ein Testsignal handelte oder nicht.
UPDATE (8.2., 22 Uhr): Zumindest Datum und Zeit der Pressekonferenz sind jetzt offiziell: Donnerstag 11. Februar, 10:30 Uhr EST
Jedenfalls ein guter Anlass, Revue passieren zu lassen, was Gravitationswellen eigentlich sind, wie man sie nachweisen kann und wie sie entstehen. Hier ist eine Visualisierung, die ich im folgenden Schritt für Schritt näher erklären möchte:
Aber erstmal etwas zum Hintergrund.
Einsteins verformbare Raumzeit
Ende November 2015 haben wir den hundertsten Geburtstag von Albert Einsteins Allgemeiner Relativitätstheorie gefeiert. Einsteins Theorie verknüpft die Gravitation – im Alltag nennen wir sie, wenn überhaupt, Schwerkraft – mit den Eigenschaften von Raum und Zeit. Frei nach einer populären Kurzfassung des US-amerikanischen Relativisten John Wheeler: Masse und Energie sagen Raum und Zeit, wie sie sich verzerren sollen; Raum und Zeit sagen den Körpern, wie sie sich bewegen sollen.
(Weitere Informationen dazu gibt’s auf Einstein Online unter Gravitation: Vom Fahrstuhl zur Raumzeitkrümmung.)
Dass Raum und Zeit sich verzerren können, hat eine direkte Konsequenz: Wird die Raumzeit-Geometrie irgendwo im Raum in geeigneter Weise gestört, kann sich diese Störung durch den Raum ausbreiten. Ich bin aus einer Reihe von Gründen dagegen, Einsteins Theorie durch ein verformbares Gummituch zu veranschaulichen, aber zumindest diesen Aspekt kann das Gummituch gut veranschaulichen: Drücke ich ein aufgespanntes Gummituch an einer Stelle mit dem Finger ein, verändert sich die Geometrie der Fläche (z.B. die Winkelsumme kleiner Dreiecke, die man auf das Tuch malt). Und nehme ich meinen Finger dann plötzlich weg, dann breitet sich von der Stelle aus, an der ich eingedrückt hatte, in alle Richtungen ein Zittern aus.
Kleine wandernde Störungen
Dass seine Theorie solche sich ausbreitenden Störungen zulässt, hat Einstein recht bald erkannt. Zur Sitzung der mathematisch-naturwissenschaftlichen Klasse der preussischen Akademie der Wissenschaften vom 22. Juni 1916 legte er dazu den Beitrag “Näherungsweise Integration der Feldgleichungen der Gravitation” vor.
Physikern kam das, was Einstein präsentierte, in einer Hinsicht recht bekannt vor. Die Gleichungen sehen denen des Elektromagnetismus sehr ähnlich. Und beim Elektromagnetismus folgt ja ebenfalls die Existenz von Störungen, die sich mit Lichtgeschwindigkeit ausbreiten: elektromagnetischen Wellen, zu denen sowohl das Licht zählt, das wir direkt wahrnehmen, als auch Radiowellen, Wärmestrahlung und Röntgenstrahlung.
Lange Zeit war allerdings unklar, ob Einsteins Gravitationswellen tatsächlich ein physikalisches Phänomen sind. Die Allgemeine Relativitätstheorie lässt den Physikern große Freiheiten, eine konkrete Situation zu beschreiben (“Freiheit der Koordinatenwahl”). Waren Gravitationswellen tatsächlich Änderungen der Eigenschaft von Raum und Zeit, oder änderte sich dabei lediglich unsere Beschreibung von Raum und Zeit, ohne physikalische Auswirkungen? Einige Ausläufer dieser Diskussion zogen sich bis in die 1980er Jahre. Mehr dazu in dem Buch “Traveling at the Speed of Thought” von Daniel Kennefick und in diesem Artikel desselben Autors.
Was tut sich da?
Schauen wir uns jetzt an, was bei solchen Störungen eigentlich passiert. (Was folgt sind verbesserte Versionen von Bildern und Animationen, die ich ursprünglich für den Einstein Online-Artikel Die Wellennatur der Gravitationswellen angefertigt habe, wo sich auch eine ausführlichere Beschreibung findet.)
Die einfachste Beispielsituation ist die folgende: Irgendwo im Weltraum, fernab jeder Massen (allgemeiner: jeder Gravitationsquellen) schweben kleine rote Teilchen. Das Bild gibt wieder, dass die Teilchen im Kreis angeordnet sind, jedes davon im gleichen Abstand zum Kreismittelpunkt, schwarz eingezeichnet:

Läuft jetzt die einfachste Form einer Gravitationswelle von hinten nach vorne durch diese Anordnung (einfache, ebene Gravitationswelle mit konstanter Frequenz, linear polarisiert, näherungsweise als Sinuswelle dargestellt), passiert mit den Teilchenabständen das folgende: 
Die Abstände zwischen den Teilchen ändern sich rhythmisch nach einem ganz bestimmten Muster: Jeweils in eine Richtung sind die Teilchenabstände verkürzt, senkrecht dazu sind die Abstände verlängert. Diese Kombination von Verlängerungen und Verkürzungen ist charakteristisch für die Gravitationswellen (“Quadrupolwellen”).
[Nachtrag:] Der physikalische Effekt, die hier zu sehen ist, sind die Abstandsänderungen zwischen den Teilchen. Um daraus eine Animation zu machen, trage ich alle Abstände relativ zu dem Teilchen in der Mitte auf. Ich hätte aber ebenso gut ein anderes Teilchen als Bezugspunkt nehmen könnnen.]
Die Abstandsänderungen (entsprechend der Stärke [Amplitude] der Gravitationswelle) sind hier, das muss man gleich dazu sagen, extrem übertrieben dargestellt. Eine realistische Welle würde selbst den riesigen Abstand von der Erde zur Sonne bei ihrem Durchmesser lediglich um eine Strecke verlängern bzw. verkürzen, die kleiner ist als der Durchmesser eines Wasserstoffatoms.
Von der Schwingung zur Welle
Die obige Animation ist genau genommen eine Gravitationsschwingung: mit der Zeit verändern sich die Verzerrungen, und z.B. die senkrechten Abstände werden abwechselnd maximal gedehnt und maximal gestaucht.
Die Wellennatur sehen wir erst, wenn wir verfolgen, wie sich solche Störungen, solche Schwingungen durch den Raum ausbreiten. Analog dazu, wie wir bei einer Wasserwelle einen Wellenberg verfolgen, der sich auf einem See oder im Meer ausbreitet, können wir bei der einfachen Gravitationswelle z.B. die maximale Streckung in senkrechter Richtung verfolgen.
Entsprechend verändern wir die obige Animation: Anstatt eines Kreises von frei schwebenden Teilchen betrachten wir viele hintereinanderliegende solcher Teilchenkreise, die insgesamt so etwas wie einen Zylinder bilden: 
Die Punktwolke ist ziemlich unübersichtlich. Daher verbinde ich benachbarte Teilchen mit blauen Linien und ziehe zwischen diesen Linien noch eine durchscheinende weiße Fläche ein: 
Vorsicht: Die zusätzlichen Strukturen, die blauen Linien und weißen Flächen, dienen nur der Orientierung! Im Gegenteil ist es dafür, dass die Gravitationswelle ungestört wirken kann, wichtig, dass die Teilchen eben nicht physisch verbunden sind, sondern eben frei nebeneinander schweben.
Und jetzt lassen wir auf diese Teilchen die Gravitationswelle wirken, die in diesem Bild von rechts hinten nach links vorne durch das Bild läuft, parallel zur Zylinderachse:
Wie bei einer Wasserwelle “läuft das Maximum durch den Raum” – erst erreicht der eine Teilchenkreis maximale Dehnung in senkrechte Richtung, dann der Teilchenkreis etwas weiter links, dann der noch etwas weiter links und so weiter.
Besonders deutlich werden die wandernden Gravitationswellenberge, wenn wir die Anordnung direkt von der Seite betrachten: 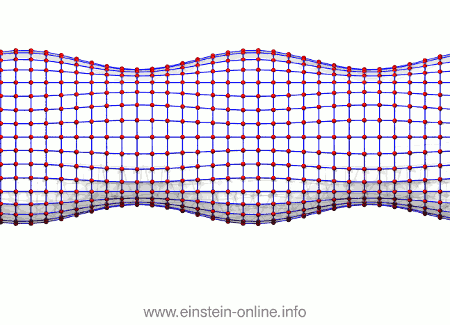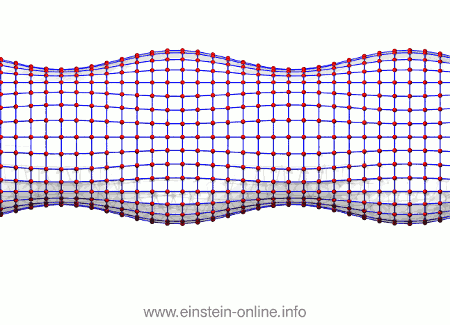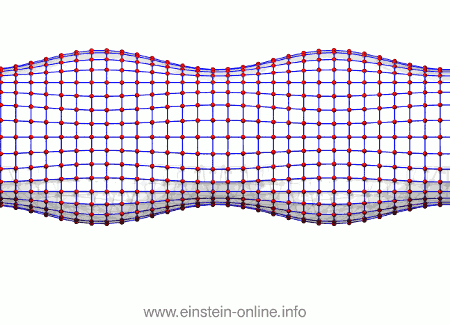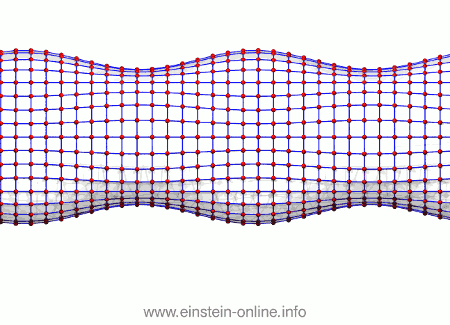
Und da haben wir unsere Gravitationswelle in einfachster Version: Sich ändernde Teilchenabstände nach einem Muster, das sich durch den Raum ausbreitet.
Genauer gesagt ist das eine “linear polarisierte” Welle. Es gibt noch andere einfache Möglichkeiten, etwa eine Gravitationswelle, die sich quasi durch den Raum “schraubt”, wie hier dargestellt (“zirkulär polarisierte Welle”): 
Ein wirkliches Signal wird im allgemeinen einen komplizierteren Verlauf haben, mit einer Überlagerung einfacher Wellen, deren Amplituden sich zudem mit der Zeit verändern. Aber das Grundprinzip wird schon an den hier gezeigten Animationen deutlich.
Stellt sich gleich die nächste Frage: Wie kann man den Durchgang einer Gravitationswelle nachweisen? Darum geht es dann in Teil 2: Gravitationswellendetektoren und wie sie Gravitationswellen nachweisen


Sehr schöne Veranschaulichung, vielen Dank.
Sehe ich das aber richtig: Wenn sich durch Gravitationswellen Teilchenabstände verändern, wird nicht der Raum an sich gekrümmt, oder?
Bei der Frage, welchen Abstand zwei Teilchen haben, geht immer auch die Geometrie des Raumes ein. Und die ändert sich in der Tat; im Falle von Gravitationswellen wird der Raum auch gekrümmt.
Argh, wieder in die Falle getappt: wichtig ist, dass die Raumzeit gekrümmt ist (die ein mathematischer Raum, aber nicht der dreidimensionale Raum ist). Dabei sind die Zeit-Verzerrungseffekte deutlich wichtiger als die Raumkrümmung.
Die Gravitationswellenvisualisierung mit Teilchen führt zur Frage: Spüren diese Teilchen eine Kraft, wenn sie durch die Gravitationswelle aus ihrer Ruheposition ausgelenkt werden? Nehmen wir dazu an, die Teilchen wären Atome in einem Kristall. Durch diesen Kristall (zb. ein Metall oder Salz) läuft eine Gravitationswelle und führt zu kleinen Auslenkungen der Gitteratome. Erzeugen die Auslenkungen eine Rückstellkraft? Intuitiv würde ich das verneinen, denn der Raum selbst verzerrt sich ja. Die Teilchen bewegen sich kräftemässig gesehen nicht, sondern sie bewegen sich in einer Art Geodäte.
Was “der Raum selbst” macht und was die Teilchen darin machen lässt sich nicht so einfach auseinanderhalten (gleiches Problem gibt es bei der kosmischen Expansion). Jedenfalls bewegen sich die freien Teilchen auch beim Durchgang von Gravitationswellen in der Tat auf Geodäten (zumindest in der vereinfachten Darstellung). Und bei Teilchen in einem Festkörper wirkt die Gravitationswelle in der Tat wie eine kleine zusätzliche Kraft.
Markus Pössel schrieb (8. Februar 2016 17:06):
> Was “der Raum selbst” macht und was die Teilchen darin machen lässt sich nicht so einfach auseinanderhalten
Ganz recht.
Die im Beitrag beschriebene und gezeigte Animation hat allerdings die Schwäche, dass sie sich der Vorstellung/Interpretation zumindest nicht entschieden entgegenstellt, dass ausschließlich „die Teilchen alleine etwas machen“, nämlich ihre (chronometrischen) Abstandsverhältnisse gegenüber einander in charakteristischer Weise ändern, ganz ohne dass „der Raum (selbst) irgendetwas macht“ außer „seine Krümmung“ ganz ausdrücklich nicht zu verändern (sondern unverändert z.B. so gut wie völlig flach zu bleiben).
Wer angesichts der gezeigten Animation in dieser Vorstellung befangen wäre, müsste natürlich folgern, dass die abgebildeten „roten Teilchen“ nicht ganz frei wären, sondern in geeigneter Weise geschubst wurden und/oder miteinander wechselwirkten. Diese Intuition widerspräche zwar sicherlich der korrekten ausdrücklichen Versuchsanordnung („von frei schwebenden Teilchen“);
aber das bedeutet für den in der genannten Vorstellung und Intuition befangenen Betrachter ja vor allem, dass die vorgeschlagene Versuchsanordnung und die entsprechend korrekt gezeigte Animation nicht besonders intuitiv sind.
Das geht besser;
es lässt sich sehr wohl darstellen, dass „der Raum etwas macht“ (wenn auch selbstverständlich nicht unabhängig davon „was die Teilchen (darin) machen“);
und Synges „five point curvature detector“ legt nahe, wie das geht; zum Beispiel:
an Stelle jedes einzelnen „roten Teilchens“ setzte man fünf (noch erheblich kleinere, voneinander getrennte) Teilchen; nennen wir die Mitglieder je eines solchen Grüppchens A, B, H, J und K.
Diese fünf Beteiligten bilden offensichtlich 10 Paare. Zu fordern wäre (um eine intuitivere Darstellung einer Gravitationswelle zu erhalten), dass 9 dieser Paare stets gleiche (chronometrische) Abstände untereinander haben sollten, während der (chronometrische) Abstand des verbleibenden zehnten Paares etwas größer sein sollte (nämlich mehr oder weniger gleich der Höhe bzw. Diagonale eines Doppeltetraeders und sich geeignet periodisch verändern sollte.
Diese Darstellung braucht keine ausdrückliche zusätzliche Forderung nach (eventueller) „Freiheit“ oder (bestimmter) „Unfreiheit“.
Es wird jedenfalls verdeutlicht:
„Im unveränderlichen (z.B. immer ganz flachen) Raum ginge das gar nicht“,
also dass neun paarweisen Abstände zwischen fünf Beteiligten fixiert blieben während nur der Abstand des zehnten Paares sich (systematisch, oder überhaupt) verändert.
p.s.
Man beachte auch den Zusammenhang zwischen der Darstellung dessen, was man zu messen versucht, und der Bedeutung und Nachvollziehbarkeit von Messwerten, die man ggf. erhält.
Eine Animation ohne implizite Koordinatenwahl, die gleichzeitig unser räumliches Anschauungsvermögen nutzt, dürfte unmöglich sein. Ich halte die hier gezeigte Animation für sinnvoll. Dass Sie die Dinge gerne ins abstraktere, damit sicher der mathematischen Beschreibung nähere, aber auch deutlich schwerer verständliche treiben möchten, ist mir schon klar. Diese Forderung stellen Sie ja in der einen oder anderen Form so ziemlich unter jedem meiner entsprechenden Blogbeiträge.
Markus Pössel schrieb (10. Februar 2016 14:10):
> Eine Animation ohne implizite Koordinatenwahl, die gleichzeitig unser räumliches Anschauungsvermögen nutzt, dürfte unmöglich sein. Ich halte die hier gezeigte Animation für sinnvoll
Die Möglichkeiten, die mir in einem SciLogs-Kommentar gegeben sind, um aufzuzeigen, welche Art von Animation ich zur Darstellung von Gravitationswellen für (bedeutend) sinnvoller halte, habe ich mit meinem obigen Kommentar leider schon so gut wie ausgeschöpft.
(Falls und wenn sich bei Wikipedia und/oder StackExchange endlich die Möglichkeit bieten sollte, pstricks-Befehle graphisch rendern zu lassen, so wie alle anderen LaTeX-Befehle auch, dann werde ich gern davon entsprechend Gebrauch machen.)
> Dass Sie die Dinge gerne ins abstraktere, damit sicher der mathematischen Beschreibung nähere, aber auch deutlich schwerer verständliche treiben möchten, ist mir schon klar. […]
Das so eine Äußerung geeignet ist, mir die Stimmung zu vermiesen, dürfte klar sein.
Denn sogar einem Markus Pössel ist zuzutrauen, doch (eigentlich, leicht genug) zu verstehen:
– dass Kimme, Korn, und Bullseye („die Zehn in der Schießscheibe“) entweder zueinander gerade lagen, oder ansonsten nicht;
– dass die vier Enden der Beine eines Tisches zueinander eben lagen, oder ansonsten nicht;
– dass fünf Interferometerspiegel eines Syngeschen Krümmungsdetektors zueinander flach lagen, oder ansonsten nicht; …
– dass eine Astronautin in einer („Rindlerschen“) Rakete und ihr Schatzi zu Hause entweder gegenseitig miteinander telefonierten, oder ansonsten nicht;
– bzw. dass jeder (für sich selbst, verbindlich) beurteilen kann, was er zusammen wahrgenommen hatte, oder was nicht.
Und einem Barry Barish nicht minder.
Vom Konzept mögen solche Dinge leicht zu verstehen sein. Die richtige Verknüpfung ist schon etwas anderes. Und als dreidimensionales Exponat bekommt man es zum Teil auch noch hin. Aber das Ganze so (projiziert-zweidimensiona) zu visualisieren, dass es einfach nachvollziehbar ist, halte ich für sehr schwierig. Ich bin mir z.B. schon nicht sicher, ob meine Gravitationswellendetektoren in Teil 2 da nicht zu kompliziert sind.
Markus Pössel schrieb (10. Februar 2016 17:57):
> das Ganze so (projiziert-zweidimensiona) zu visualisieren, dass es einfach nachvollziehbar ist, halte ich für sehr schwierig.
Ich nehme das gern als Aufforderung und Einladung (vielen Dank!), nochmals etwas ausführlicher zu skizzieren (wenn auch unter den hier gegebenen Möglichkeiten leider nur rein verbal), was ich dahingehend für das Einfachste halte:
Man zeichne (auf die zur Verfügung gestellte 2-Dimensionale Zeichenfläche) die Projektion eines regulären Doppel-Tetraeders „im Flachen“; also
– (die Projektionen von) fünf Ecken (entsprechend der relevanten Anzahl „five“ in „five point curvature detector“), so dass
– neun der zehn paarweise Abstände zwischen diesen fünf Ecken alle gleich sind
(schreiben wir für den Wert dieses Abstands „a“);
– und so dass für den Abstand zwischen dem verbleibenden zehnten Paar (Wert „b“) zwangsläufig gilt:
b = √[ 8/3 ] a.
Man zeichne entsprechend (die Projektionen von) neun gleichen („externen“) Kanten als gerade Linien,
d.h. insgesamt etwa so wie hier schon vorgemacht (wenn auch leider ohne editier- bzw. nachnutzbaren Quellcode): https://de.wikipedia.org/wiki/Datei:Hexahedron5.svg
Um nun zu verdeutlichen, dass der Abstand „b“ des zehnten Paares “im Krummen eigentlich“ nicht gleich dem √[ 8/3 ] fachen der anderen (neun gleichen) Abstände „a“ sein kann (bzw.: ist), sondern dass tatsächlich/chronogeometrisch
– Entweder: √[ 8/3 ] a < b < 2 a,
– oder stattdessen: a < b < √[ 8/3 ] a,
zeichne man die verbleibende zehnte „interne“ Kante, und nur diese, als (Projektion von einem) entweder deutlich erkennbar gedehnten, oder stattdessen gestauchten, mehr oder weniger voluminösen Stück Gummi.
Strahlt eigentlich jedes massebehaftete Teilchen ständig Gravitationswellen aus? Wenn ja müsste dessen Masse eigentlich ständig abnehmen, falls es nicht gleichzeitig fremde Gravitationswellen absorbieren kann.
Oder anders gefragt: Wenn sich die Gravitation irgendeines Körpers mit Lichtgeschwindigkeit ausbreitet, geschieht das stets in Form von Gravitationswellen?
Darauf komme ich später noch, in Kürze: Nein, man muss Teilchen in bestimmter Weise beschleunigen, damit Gravitationswellen entstehen. (Fast, aber nicht ganz analog zum Elektromagnetismus – EM-Wellen entstehen ja auch dann, wenn elektrische Ladungen beschleunigt werden.) Zur Gravitation von Körpern: Nur Störungen bzw. Änderungen des Gravitationsfeldes entsprechen Gravitationswellen. (Wieder analog zum Elektromagnetismus.)
Sie beschreiben die geometrische Struktur der Wirkung der Gravitationswelle auf Teilchen. Wie sieht aber die statische geometrische Struktur der Ursache aus? Können Sie die geometrische Struktur des Raumes beschreiben, ohne das Teilchen dazu Verwendung finden müssten? Können Sie den Motor benennen, der in einem “leeren” Raum die Gravitationskraft produziert? Ich meine, nur allein ein Raum-Kollaps kann eine Gravitationswelle produzieren. Diese Welle setzt sich als Sprungfortsetzung auf Quantenebene nichtlinear durch den Raum fort.
Viele Grüße
Uwe Friebel
Zu den Gravitationswellenquellen kommt in einem späteren Teil noch etwas. Im Prinzip produzieren z.B. alle Massen, die umeinander rotieren, eine Gravitationswelle. Wenn man die Geometrie tatsächlich nachweisen will, muss man schon Teilchen, Licht oder so etwas verwenden. Wenn es wirklich nur um Beschreibung geht: Das leistet in der Allgemeinen Relativitätstheorie ein abstraktes Objekt namens Metrik. Aber beschreiben ist noch nicht gleich messen/nachweisen, und der Nachweis dürfte diese Woche gerade das Spannende werden!
Vermutlich habe ich immer noch nicht wirklich verstanden, was Gravitationswellen sind. Aber eigentlich ist es doch das gleiche wie bei EM-Wellen: Man braucht einen Oszillator, der eine Feldgröße (evtl. periodisch) verändert, um eine Welle zu erzeugen. Bei Gravitationswellen könnte man zwei einander umkreisende Sterne nehmen und die Gravitation (und damit die periodisch veränderliche Verzerrung der Raumzeit) an einem Ort in der Nähe messen. Dann gibt es noch die RT, die verbietet, dass sich eine Änderung der Gravitationskraft unendlich schnell durch den Raum ausbreitet, und schon haben wir alle Zutaten für eine Welle. Natürlich ist die Messung aufgrund der schwachen Gravitation eine enorme Herausforderung, aber es ist eine technische Herausforderung, keine prinzipielle. Man muss Längenänderungen auf einer subatomaren Skala messen und erst einmal herausfinden, wie das geht. Darüber hinaus haben wir das Problem, dass es vermutlich keine genügend starken “Gravitations-Oszillatoren” in der Nähe gibt, aber dass generell im Universum einander umkreisende Sterne existieren, ist doch erwiesen. Nach meinem (vermutlich irgendwie falschen) Verständnis ist die Existenz von Gravitationswellen dadurch sicher gestellt, dass sich a) die Gravitation an einem Ort ändern kann, und b) die Änderung sich nur mit endlicher Geschwindigkeit auf die Umgebung auswirkt. An beidem besteht kein Zweifel. Irgendwie gelange ich da nicht zum Kern der Sache. Was ist der besondere Kick bei den Gravitationswellen? Warum zweifeln die Physiker an deren Existenz?
Beim Higgs war mir das irgendwie klarer. Es war eine wunderschöne Theorie, zu schön um falsch zu sein, aber dennoch ein Modell, das praktisch aus dem nichts entstanden war und bis zum experimentellen Nachweis angezweifelt werden musste. Wir konnten nicht sicher sein, dass es existiert. Gravitationswellen hingegen sind doch eine unvermeidliche Konsequenz der vielfach experimentell bestätigten RT.
Nur zur Vorsicht: Das ist keine Kritik an der Suche nach Gravitationswellen. Ich will nur herauszufinden, was ich nicht verstanden habe.
Die Antwort ist ein eigener Blogbeitrag geworden: https://scilogs.spektrum.de/relativ-einfach/gravitationswellen-warum-die-aufregung/
Toll, ganz ganz toll! Vielen Dank für die große Mühe und Leidenschaft, die Du da reinsteckst! 🙂
Ich habe da ein Verständnisproblem:
Wie kann eine solche Apparatur (LIGO), auf Gravitationswellen überhaupt reagieren? Sie ist ja nicht ein außenstehender Beobachter, sondern auf sie wirkt die Gravitationswelle selbst. Damit müsste eine Verkürzung des Abstandes zweier Spiegel auch gleichzeitig eine Dehnung der Zeit zur Folge haben und beide Effekte zusammen müssten den Effekt zu Null ausgleichen? Also: Wie kann ein Meßapparat, auf den selbst eine GW wirkt, überhaupt was messen? Ein Astronaut, der in der Nähe eines schwarzen Loches ist, merkt ja auch nicht, dass seine Zeit “langsamer” verläuft. Das sieht doch erst ein außenstehender Beobachter.
Ich kann mir das nur so erklären, dass LIGO überhaupt etwas gemessen hat: Da die Graviationswelle eine beschränkte Ausbreitungsgeschwindigkeit hat, wirkt sie nicht instantan auf die komplette Anlage. Aber wenn das der Grund ist, warum braucht man dann zwei senkrecht aufeinander stehende Arme? Diese gibts doch angeblich nur deshalb, weil Graviationswellen transversal polarisiert sind und daher die Raumzeitkrümmung in beiden Armen unterschiedlich stark sein soll?
Vielleicht mag jemand erklären, wo mein Missverständnis liegt.
Das ist in Teil 2 mit einigen Animationen erklärt: https://scilogs.spektrum.de/relativ-einfach/gravitationswellendetektoren-wie-sie-funktionieren-gw-teil-2/
Tut mir leid, das erklärt nur die Stauchung/Streckung des Raumes. Eine Gravitationswelle beeinflusst aber die Raumzeit, also auch die Zeit. Darauf wird leider im Teil 2 überhaupt nicht eingegangen.
Meines Erachtens wird entlang der Laserstrecke die Zeit genau in dem Maße gedehnt wie die Strecke räumlich gekürzt wird, damit die Konstanz der Lichtgeschwindigkeit auf der Strecke gewahrt bleibt. Die Folge wäre, dass ein lokaler Beobachter – also die Meßapparatur – überhaupt nichts merkt.
Das ist genau wie bei einem Astronaut, der mit hoher Geschwindigkeit fliegt und Kürzungen von Längen im Raum überhaupt nicht bemerkt, sondern nur ein Beobachter von weit draußen.
Tut mir leid, ich vermisse die Beschreibung, wie sich die Zeit innerhalb der Gravitationswelle ändert. Daher ist für mich diese Erklärung unzureichend.
Teil 2 geht aber leider nur auf die Veränderung des Raumes, aber nicht auf die Änderung der Zeit innerhalb der Gravitationswelle ein. Es wird aber die Raumzeit geändert, nicht nur der Raum. Meines Erachtens müsste sich eine Dehnung des Raumes entlang einer Strahlachse genau wegen der Konstanz der Lichtgeschwindigkeit eine Stauchung der Zeit zur Folge haben.
Resultat: Man kann als *lokaler* Beobachter überhaupt keinen Effekt erkennen.
Ich habe genau das beschrieben, was die Relativitätstheorie für diese Situation aussagt. Und da lassen sich Gravitationswellen in geeigneten (und naheliegenden) Koordinaten eben als genau die hier dargestellten Störungen der Raumgeometrie beschreiben, ohne jegliche Beeinflussung der Zeit. Und der Effekt für einen Beobachter am Detektor, der das Eintreffen der Laserpulse verfolgt und Änderungen sieht, ist das Ergebnis.
Wie würden wir Menschen die Verschmelzung der schwarzen Löcher in einer viel kleineren Entfernung gravitativ wahrnehmen? Gibt es dazu Vorstellungen?
Gar nicht, in Sonnenentfernung 150 Mio km wäre die relative Änderung etwa 0,000001,
das sind etwa 2 Tausendstel mm auf die Körpergröße.
2 schwarze Löcher in Sonnendistanz würden unser Planetensystem zerstören allerdings nicht wegen den entstehenden Gravitationswellen, sondern wegen der Gravitationskraft. Ob das nun 1 oder 2 schwarze Löcher in Sonnendistanz wären, ändert praktisch nichts am Resultat.
Ähm, was haben Rote Riesen mit der Verschmelzung von SL zu tun?
Die Graviwellen würden wir nicht spüren, aber es fehlen abrupt 5%
der anziehenden Masse. Wenn es eine zentrale Masse wäre, die
umkreist wird, wären die Umlaufbahnen ebenso abrupt betroffen.
OK, das müßte auch noch “gravitativ” hinzugeantwortet werden.
Lieber Herr Pössel!
spannend, was da so entdeckt wurde. Gratulation an all die Beteiligten.
Tja, ENT-DECKEN, weil es ja eh immer da war bzw da ist.
Folgendes bitte ich Sie, so gut wie möglich zu beantworten, und zwar:
Für mich ist es verständlich, wenn man einen Stein ins Wasser wirft, dass sich darin, weil das Wasser ja Masse ist, Wellen ausbreiten können. Das ist verständlich.
Wie kann man aber verstehen, dass sich im Universum etwas Ausbreiten kann, in dem Fall die Gravitationswellen, wenn im All ja relativ nichts, ausser dieser Weite mit ein paar Planeten und dazwischen dieser Leere, vorhanden ist. 😉
Wie könnte man dieses Nichts, indem sich darin etwas fortbewegen kann, ein wenig beschreiben. Es könnte doch mit diesem gelungen Experiment gesagt werden, dass das NICHTS nicht Nichts ist, sondern doch etwas, aber sich in Worte nur schwer fassen lässt. Für mich als Laie ist mit diesem Experiment mitunter auch der Nachweis erbracht, dass es nicht Nichts gibt. Könnte man dieses Nichts als “Energie-Masse” bezeichnen, die durch ein Ereignis weit draussen im Universum in Bewegung gebracht wird und sich dadurch die Gravitationswellen nachweisen lassen?! Vielen herzlichen Dank im Voraus für ihre Stellungnahme.
Anscheinend hat sich eine Vakuumröhre gestaucht, gegenüber der anderen, müßte nicht nach der ART das Licht des Lasers mitgekrümmt werden, daß man die Längenänderung eigentlich so gar nicht wahrnehmen kann?
Wegen dem Bruch in der SRT bzw. anderer Ursache. Es wirkte auf alle Fälle mehr Kraft auf die gestauchte Röhre oder?
Ich hab nochmal beim MPI für Gravitationsphysik in Hannover angerufen. Die Lichtgeschwindikeit bleibt konstant, es sind Laserimpulse.
Und es wirkt eine Kraft, die nicht meßbar ist. MfG
@Markus Pössel
Wie ist das eigentlich mit dem ‘näherungsweise’ genau gemeint bei der Formulierung »(einfache, ebene Gravitationswelle mit konstanter Frequenz, linear polarisiert, näherungsweise als Sinuswelle dargestellt)«? Die hier und im verlinkten Einstein-Online-Artikel gegebenen Ausführungen legen für eine mit Geschw. c = 1 in x-Richtung fortschreitende, linear polarisierte PW den Ansatz
g = η + h sin(ω(t−x)) [dy² − dz²]
nahe, wobei η die Minkowski Metrik bezeichne. Jedoch will mir scheinen, dass dieser Ansatz gar keine Lösung von Ric = 0 liefert, oder habe ich mich da möglicherweise verkalkuliert? Falls also die Sinuswelle nur als eine Art “heuristische Näherung” zum Zwecke der Veranschaulichung dienen sollte, findet das fragliche ‘näherungsweise’ damit natürlich seine Erklärung. Andererseits ist im Einstein-Online-Artikel von ‘näherungsweise’ nirgendwo die Rede, und es wird dort der Eindruck erweckt, die Sinuswelle sei eine zwar simple, aber doch exakte Lösung.
Ich will ja nicht ausschliessen, dass ich gerade ein Brett vor dem Kopf habe und ständig etwas übersehe, aber im Moment tendiere ich zu der Einschätzung, dass die Darstellung noch nicht so unmissverständlich ist, wie es wünschenswert wäre.
Damit ist die übliche lineare Näherung gemeint – Metrik als flach plus kleine Störungen h_{mu nu} geschrieben und dann nur lineare Terme in h_{mu nu} behalten, quadratische und höhere Terme vernachlässigt.
In dieser Näherung wird der Ricci-Tensor bei geeigneter Eichung (man hat beim h_{mu nu} noch Transformationsmoeglichkeiten) gerade proportional zur Wellengleichung für jede Komponente h_{mu nu} (genauer hängt da noch ein Spurterm mit drin, der in dem hier betrachteten Sonderfall aber verschwindet).
Eine exakte Lösung ist das nicht, sondern nur eine lineare Näherung – da die h_{mu nu} weiter entfernt von der Quelle aber sehr klein sind, ist es eine sehr gute Näherung mit entsprechend weiten Anwendungsmöglichkeiten.
Chrys schrieb (26. Februar 2016 23:04):
> […] x […]
Oh, Koordinaten transformieren kann ich gut.
Ersetze doch mal zum Beispiel:
t → t,
x → x,
y / (1 + Sqrt[ h Sin[ ω (t – x) ] ]) → y,
z / (1 – Sqrt[ h Sin[ ω (t – x) ] ]) → z.
Diese Ersetzung kann sicherlich Vieles vereinfachen, was unter Verwendung dieser Koordinaten ausgedrückt werden könnte. (In wie fern diese Ersetzung allerdings zu eventueller Verständlichkeit beiträgt, sei dahingestellt.)
@Frank Wappler
War das jetzt ein akuter Anfall von Koordinatenallergie? Ich wünsche auf jeden Fall gute Besserung und baldige Genesung. 😉
Chrys schrieb (28. Februar 2016):
> […] Koordinatenallergie?
Lieber ansteckend Koordinaten-frei als anmaßend maßlos.
p.s.
> […] mit einer ‘ebenen Gravitationswelle’
Damit ist in diesem SciLog wohl nicht mehr als der „Koordinatenartefakt“ gemeint, dass sich
&8477;^4
ohne Weiteres als
&8477;^(2+2)
Schreiben lässt.
Chrys schrieb (28. Februar 2016):
> […] Koordinatenallergie?
Lieber ansteckend Koordinaten-frei als anmaßend maßlos.
p.s.
> […] mit einer ‘ebenen Gravitationswelle’
Damit ist in diesem SciLog wohl nicht mehr als der „Koordinatenartefakt“ gemeint, dass sich
&8477;^4
ohne Weiteres als
&:8477;^(2+2)
Schreiben lässt.
Chrys schrieb (28. Februar 2016):
> […] Koordinatenallergie?
Lieber ansteckend Koordinaten-frei als anmaßend maßlos.
p.s.
> […] mit einer ‘ebenen Gravitationswelle’
Damit ist in diesem SciLog wohl nicht mehr als der „Koordinatenartefakt“ gemeint, dass sich
ℝ^4
ohne Weiteres als
ℝ^(2+2)
schreiben lässt.
@Markus Pössel
Die Bezeichnung ‘ebene Gravitationswelle’ kann prinzipiell in zwei verschiedenen Bedeutungen daherkommen, und gemeint sein kann dann i) eine lineare ebene GW, im Sinne einer Lösung der linearisierten Feldgl., ober ii) eine exakte ebene GW, womit in der GR eine spezielle Klasse exakter Lösungen bezeichnet wird. Zumeist wird aus dem jeweiligen Zusammenhang unmittelbar ersichtlich, wie es gemeint war, aber bisweilen muss man auch ein wenig rätseln.
Wenn nun der Autor des Einstein-Online-Artikels so etwas schreibt wie “Die entsprechenden Gravitationswellen heißen dementsprechend auch Sinuswellen,” dann darf man aus verschiedenen Gründen eigentlich darauf wetten, dass er sich im selben Sinnzusammenhang mit einer ‘ebenen Gravitationswelle’ gewiss auf eine linearen Fall i) beziehen wird. Doch wenn uns derselbe Autor dann eine “einfache, ebene Gravitationswelle mit konstanter Frequenz, linear polarisiert, näherungsweise als Sinuswelle dargestellt” präsentiert, macht einen das ‘näherungsweise’ dabei irgendwie stutzig, denn die Sinuswelle wäre im zuvor genannten Sprachgebrauch ja selbst schon eine ebene GW mit all den aufgezählten Eigenschaften, und das nicht nur näherungsweise. War es also hier vielleicht doch anders gemeint? Ich schätze mal nein, aber so ganz sicher bin ich mir da noch nicht.
Wunderschöne Visualisierung. Verwirrt hat mich allerdings eine Aussage bei der Anordnung in der dritten Grafik. Dort steht dass sich die Teilchenabstände ändern. Physiker gehen bei der Beschreibung der Thematik anscheinend immer stillschweigend davon aus, dass die Abstände über die Ausbreitungsgeschwindigkeit des Lichtes gemessen werden. Als Laie stelle ich mir erfahrungsgemäß immer vor, dass die Teilchenabstände mit einem Meter messbar wären.
Markus Pössel schrieb (8. Februar 2016):
> […] Die einfachste Beispielsituation ist die folgende:
> […] fernab jeder Massen (allgemeiner: jeder Gravitationsquellen)
> […] eine[] Kreis[] von frei schwebenden Teilchen
> Läuft jetzt die einfachste Form einer Gravitationswelle von hinten nach vorne durch diese Anordnung (einfache, ebene Gravitationswelle mit konstanter Frequenz, linear polarisiert, näherungsweise als Sinuswelle dargestellt) ), passiert mit den Teilchenabständen das folgende:
> Die Abstände zwischen den Teilchen ändern sich rhythmisch nach einem ganz bestimmten Muster: Jeweils in eine Richtung sind die Teilchenabstände verkürzt, senkrecht dazu sind die Abstände verlängert.
Laut Einstein (also zumindest im Rahmen der Relativitätstheorie) gilt offenbar:
(Sicherlich schließt das ggf. auch Bestimmungen zeiträumlicher Nicht-Koinzidenz ein; insbesondere hinsichtlich von unterscheidbaren Beteiligten/Teilchen, deren zeiträumliche Beziehungen untereinander als „Abstände“ charakterisiert sind.)
Wie (falls überhaupt) ist demnach insbesondere die Versuchsanordnung „ frei schwebend“ durch Feststellungen von Koinzidenzen (bzw. von Nicht-Koinzidenzen) definiert und ggf. zu gewährleisten?
p.s.
Die selbe Frage stellt sich übrigens (und wohl nicht ganz zufällig) hinsichtlich der Versuchsanordnung der sogenannten
“geometrodynamischen Uhr“-Konstruktion nach Marzke und Wheeler.
Markus Pössel schrieb (8. Februar 2016):
> […] Verlängerungen und Verkürzungen […] ändern sich rhythmisch […]
> Nachtrag: […] hier zu sehen […] sind die [ … Entfernungen] relativ zu dem Teilchen in der Mitte […] Ich hätte aber ebenso gut ein anderes Teilchen als Bezugspunkt nehmen können.
So wie die oben gezeigten Animationen auf meinem Bildschirm ablaufen, besteht darin doch ein Unterschied zwischen den Dauern der verschiedenen Teilchen, die Wiederholungen der genannten “rhythmischen” Abläufe kennzeichnet:
Bezeichne T die entsprechende Periodendauer des “Teilchens in der Mitte des Rings” in der Abbildung,
dann beträgt die entsprechende Periodendauer eines “Teilchens im Ring” offenbar (sofern die mir vorliegende Rechnung stimmt)
T * VollständigesElliptischesIntegralE[ (2 Pi)^2 * (A/T)^2 ] / (Pi/2),
wobei der Zahlenwert (das Verhältnis von Dauern) “A/T” ein Maß der Größe der “Verlängerungen und Verkürzungen relativ zu dem Teilchen in der Mitte” darstellt, und die VollständigesElliptischesIntegralE-Funktion ist für zunehmende Argument-Werte fallend; beginnend mit (Pi/2) für Argument A/T = 0.
Die “Rhythmus“-Periodendauer eines “Teilchens im Ring” ist demnach i.A. (nämlich offenbar für 28 der 32 abgebildeten) zumindest ein wenig kleiner als T; für die restlichen 4 aber gleich T.
Die Abbildung erscheint folglich nicht ganz exakt “eben so gut” hinsichtlich aller abgebildeten Teilchen.
Frage:
Ist diese offenbare Ungleichheit, so gering sie im konkreten Fall auch sein mag, nur in der Abbildung zu finden, oder trifft sie auch auf das System von Teilchen zu, das abgebildet wurde?
Die Abstände basieren alle auf derselben Sinusfunktion, und die Animation mit dem Kreis von Teilchen ist ein animiertes Gif, das sich nach jedem Durchgang wiederholt.
Insofern: Doch, die Periode ist für alle Teilchen die gleichen. Per Konstruktion und per Umsetzung. Keine Ahnung, wie Sie auf die gegenteilige Einschätzung kommen.
Markus Pössel schrieb (12. Juni 2016 18:21):
> Die [Entfernungen] basieren alle auf derselben Sinusfunktion
Also vermutlich (man korrigiere mich bitte, falls ich mich irre) basierend auf der Sinusfunktion angewandt auf Argumente, die sich lediglich durch konstante Phasen unterscheiden, die spezifisch bzgl. bestimmter Paare der abgebildeten Teilchen sind). Und offenbar mit Amplituden, die für verschiedene Paare der abgebildeten Teilchen spezifisch ungleich sind.
Insbesondere erscheinen in den Animationen ja Abbildungen von fünf Teilchen (dem “im Zentrum” und bestimmten vieren “im Kreis”), deren (paarweise) Entfernungen voneinander konstant bleiben. (So dass man für diesezehn Paare tatsächlich von “Abständen” untereinander Reden könnte; sie sind ausdrücklich als zueinander starr dargestellt.) Auf alle anderen (518) Paare trifft das aber offenbar nicht zu.
Habe ich dann die Abbildung etwa falsch aufgefasst (wohlgemerkt die Abbildung; nicht unbedingt ein System mit realer Gravitationswelle, das abgebildet werden sollte), wenn ich den 28 Teilchen der Abbildung jeweils eine spezifische (i.A. von Null verschiedene, periodisch veränderlich) Geschwindigkeit in Bezug auf “das System 5 starren Teilchen” zuschreibe?
Ist es falsch, jedem der “5 starren” Teilchen die gleiche Periodendauer T zuzuschreiben,
aber den anderen “28 auf dem Kreis” stattdessen Periodendauern
“Integral von 0 bis T über Sqrt[ 1 – β^2 ]”,
die von den spezifischen, periodisch veränderlichen Werten β abhängen, aber für von Null verschiedene Amplitude der o.g. Sinusfunktion durchweg kleiner als T sind?
http://arxiv.org/abs/1606.07644
http://arxiv.org/abs/1606.07644