Einstein verstehen Teil I: Hintergrundseite
BLOG: RELATIV EINFACH

Dies ist die Hintergrundseite zum Blogeintrag Einstein verstehen: Ein Blogexperiment Teil I. Wie dort beschrieben, hat die Seite mehrere Funktionen: Sie versammelt etwaige neue Textteile, in denen Aussagen aus dem Haupttext genauer erklärt werden, sie zeigt die ursprüngliche Version des Blogeintrags – vor Einarbeitung der Änderungen, die sich aus den Kommentaren der Leser ergeben haben –, und sie dient als Sammlung für diejenigen Kommentare zum Haupttext, die ich dort nicht veröffentlicht habe, da sie der Schritt-für-Schritt-Erklärung vorgreifen oder in anderer Weise unkonstruktiv sind.
1. Vertiefungen zum Blogeintrag
Abstände im dreidimensionalen euklidischen Raum
Im Haupttext hatte ich die Formel
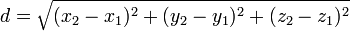
als dreidimensionale Version des Satzes von Pythagoras eingeführt. Aber wie ergibt sich diese Formel, die Koordinatendifferenzen und Abstand zweier Punkte im euklidischen Raum verknüpft?
Das folgende Bild zeigt zwei Punkte (dargestellt durch goldene Kugeln) in einem kartesischen Koordinatensystem. Genau wie im Haupttext sind die kürzesten Verbindungen jedes der drei Punkte zu den drei Koordinatenebenen eingezeichnet:
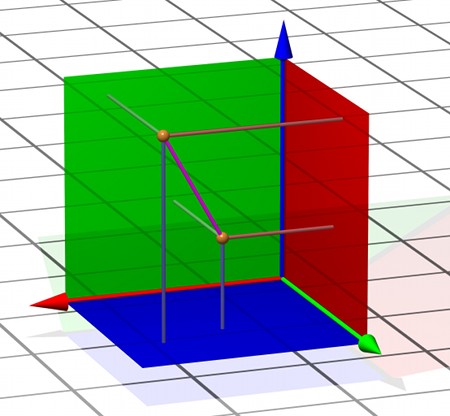
Grüne Achse bzw. grüne Ebene hatten wir x-Achse bzw. x-Ebene genannt. Analog sind blaue Ebene und Achse der y-Koordinate und die rote Ebene und Achse mit der z-Koordinate zugeordnet. Die Länge des blauen Verbindungsstücks ist der Abstand des jeweiligen Punkts von der y-Ebene und damit der y-Koordinatenwert des Punkts. Analog entsprechen die Längen von grünen und roten Verbindungsstücken den x- bzw. y-Koordinatenwerten. Die Strecke zwischen den beiden Punkten ist lilafarben eingezeichnet; ihre Länge ist der Abstand d der beiden Punkte.
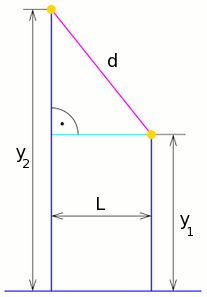 Nun nutzen wir den bereits erwähnten Umstand aus, dass auf jeder Ebene im dreidimensionalen eukldischen Raum die übliche Schulgeometrie gilt, insbesondere der übliche Satz des Pythagoras für rechtwinklige Dreiecke. Als erstes betrachten wir die Ebene, in der die beiden blauen Verbindungsstücke liegen. Rechts ist ein Ausschnitt aus dieser Ebene dargestellt. Senkrecht sind die beiden blauen Verbindungsstücke zu sehen, ganz unten waagerecht die Schnittgerade der Ebene mit der y-Ebene, und oben die lilafarbene Verbindungsgerade, die ebenfalls ganz in der Ebene liegt, da ja zwei ihrer Punkte (die oberen Endpunkte der blauen Verbindungsstücke) in der Ebene liegen.
Nun nutzen wir den bereits erwähnten Umstand aus, dass auf jeder Ebene im dreidimensionalen eukldischen Raum die übliche Schulgeometrie gilt, insbesondere der übliche Satz des Pythagoras für rechtwinklige Dreiecke. Als erstes betrachten wir die Ebene, in der die beiden blauen Verbindungsstücke liegen. Rechts ist ein Ausschnitt aus dieser Ebene dargestellt. Senkrecht sind die beiden blauen Verbindungsstücke zu sehen, ganz unten waagerecht die Schnittgerade der Ebene mit der y-Ebene, und oben die lilafarbene Verbindungsgerade, die ebenfalls ganz in der Ebene liegt, da ja zwei ihrer Punkte (die oberen Endpunkte der blauen Verbindungsstücke) in der Ebene liegen.
Für rechtwinklige Dreiecke in dieser Ebene gilt der Satz des Pythagoras, und wir schließen daraus
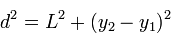
wobei L der Abstand der beiden blauen Verbindungsstücke ist. Um den Abstand L zu berechnen, schauen wir uns jetzt die y-Ebene an. Als erstes stellen wir fest, dass für jeden der beiden Punkte der Abstand des Fußpunktes des blauen Verbindungsstücks – dieser Fußpunkt liegt in der y-Ebene – von der roten z-Achse gerade die x-Koordinate des zugehörigen Punktes ist.
Am einfachsten ist das zu sehen, wenn wir wieder zur perspektivisch-dreidimensionalen Darstellung zurückgehen, einen einzigen Punkt im Raum betrachten und für diesen Punkt das grüne Verbindungsstück (Länge: x-Koordinatenwert), das blaue Verbindungsstück (Länge: y-Koordinatenwert) und den Abstand des Fußpunktes von der (roten) z-Achse betrachten (hier in türkis eingezeichnet):
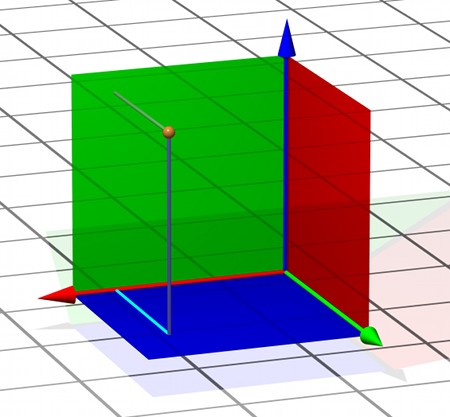
Grüne Ebene und grünes Verbindungssstück stehen senkrecht aufeinander, grünes und blaues Verbindungsstück ebenfalls, blaue Ebene und blaues Verbindungsstück (und damit blaues Verbindunggstück und eingezeichneter türkiser Abstand in der y-Ebene) auch. Damit bilden grünes Verbindungsstück und Fußpunktabstand zwei gegenüberliegende Seiten eines Rechtecks, und sind dementsprechend gleich lang. Analog lässt sich für den Abstand des Fußpunktes von der grünen Achse argumentieren: Er ist gleich dem z-Koordinatenwert des Punktes.
Damit kommen wir zurück zum Abstand L und der y-Ebene. In diese Ebene zeichnen wir die Verbindungslinie der Fußpunkte (Abstand: ebenfalls L) sowie die Abstände der Fußpunkte zu den beiden in der Ebene liegenden Achsen ein:
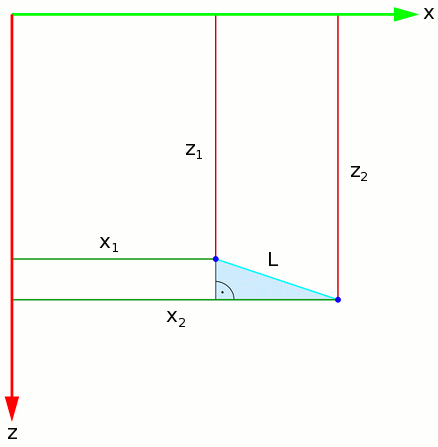
Damit können wir den Satz des Pythagoras auch in dieser Ebene anwenden: Die Länge der einen Seite des hellblau hinterlegten rechtwinkligen Dreiecks ist offenbar gerade gleich der Differenz der x-Koordinaten der beiden Punkte, also x2-x1; die Länge der zweiten Seite ist z2-z1. Mit dem Satz des Pythagoras erhalten wir für das Quadrat von L daher
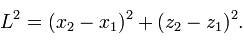
In die oben erhaltene Abstandsformel eingesetzt, ergibt sich damit tatsächlich
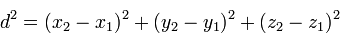
also nach Ziehen der Quadratwurzel die angegebene Beziehung
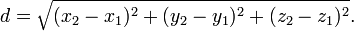
2. Originalversion des Blogeintrags
Der Weg zu einem Grundverständnis der Speziellen Relativitätstheorie beginnt in der klassischen Physik. Von dort stammen die grundlegenden Konzepte zur Beschreibung von Raum, Zeit und Bewegung, und außerdem gilt auch dort bereits eine Version des später dann so wichtigen Relativitätsprinzips. Dementsprechend beginnen auch wir hier mit der klassischen Physik, genauer: mit einem kurzen Abriss der klassischen Mechanik und direkt anschließend mit der systematischen Entwicklung der mathematischen Modelle, mit denen Physiker Raum und Zeit beschreiben.
Körper, Bewegung und Kräfte: Klassische Mechanik
Die klassische Mechanik, die beschreibt, wie sich Objekte unter dem Einfluss äußerer Kräfte bewegen, ist eine der erfolgreichsten Theorien der Physik. Als wesentlicher Bestandteil der Vorhersagen der Astronomen zu den Bahnen von Planeten, Asteroiden und Kometen hatte sie entscheidenden Anteil daran, dass sich die Physik als exakte Wissenschaft etablierte. Auch für unseren Alltag spielt sie eine wichtige Rolle, wenn auch meist im Hintergrund: Die klassische Mechanik ist z.B. Grundlage der Statik, mit deren Hilfe Architekten die Struktur von Gebäuden planen und ihre Stabilität berechnen, und der Fluiddynamik, mit deren Hilfe Flugzeuge, Schiffe und Autos entworfen werden.
Grundprinzip der klassischen Mechanik ist eine Zweiteilung der Bewegung von Objekten in natürliche Bewegung und Abweichungen von solcher natürlichen Bewegung. Damit ist folgendes gemeint: Ohne den Einfluss äußerer Kräfte bewegen sich Körper mit konstanter Geschwindigkeit entlang gerader Bahnen. In der folgenden Abbildung ist dies anhand von goldenen Kugeln gezeigt, die Körper darstellen, auf die keinerlei Kräfte wirken. Die blauen Pfeile zeigen an, wie sich die Kugeln innerhalb einer Sekunde bewegen:
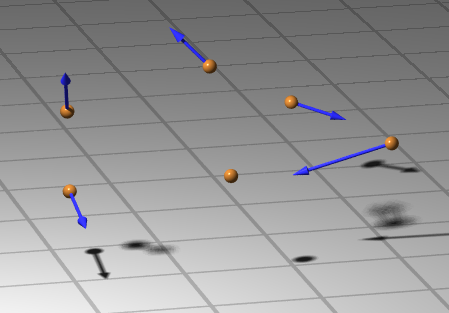
Diese Aussage heißt erstes Newton’sches Gesetz oder (Galilei’sches) Trägheitsgesetz. Dass ein Körper ruht, ist als Spezialfall “konstante Geschwindigkeit Null” in dieser Beschreibung enthalten. Geradlinige Bewegung mit konstanter Geschwindigkeit: Das ist der natürliche Bewegungszustand von Körpern.
Nächste Aussage der klassischen Mechanik ist, dass Körper nicht grundlos von ihrem natürlichen Bewegungszustand abweichen, sondern genau dann, wenn sie von einer Kraft beeinflusst werden. Wie diese Kräfte zustandekommen, ist von Kraft zu Kraft — von der Newton’schen Gravitationskraft bis zur Hook’schen Federkraft, von den Kräften, die beim elastischen Stoß wirken bis zur Reibungskraft nach Amontons — unterschiedlich.
Gemeinsam ist all diesen Kräften, welche Bewegungsänderung sie bei gegeber Stärke und Richtung bei einem Körper hervorrufen. Das zweite Newton’sche Gesetz der Mechanik besagt: Die Beschleunigung a, die ein Körper erfährt, ist gleich der auf ihn wirkenden Kraft F, geteilt durch die Masse m des Körpers. Die folgende Abbildung soll das veranschaulichen: Sie zeigt einen Körper (kleine goldene Kugel), dessen natürliche Bewegung ihn weiter geradeaus führen würde (blauer Pfeil), wenn da nicht die von einem massereichen Körper (rote Kugel) ausgehenden Schwerkraft wäre, die anziehend wirkt (roter Pfeil). Der Körper wird durch die Kraft in Richtung des massereichen Körpers beschleunigt. Er folgt nicht der geraden blauen Bahn, sondern der gekrümmten, violett eingezeichneten Bahn:
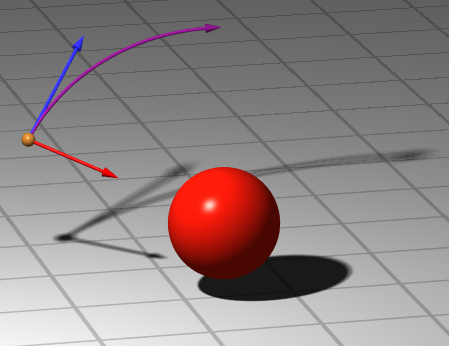
Diese Art des Zusammenspiels von natürlicher Bewegung und Anziehungskraft spielt beispielsweise eine Rolle, wenn man die Umlaufbahn eines Planeten wie unserer Erde um einen massereichen Körper wie die Sonne ableiten will.
Kräfte wirken nie isoliert: Wirkt ein Körper A mit einer Kraft F auf einen Körper B, so wirkt immer auch eine Kraft gleicher Stärke in entgegengesetzter Richtung auf den Körper A zurück. Wir kennen die Konsequenzen aus dem Alltag: Gebe ich beispielsweise einem schweren Einkaufswagen einen Schubs, dann spüre ich, wie mein eigener Körper in die Gegenrichtung gedrückt wird. Dies ist das dritte Newton’sche Gesetz, auch in der halblateinischen Version actio gleich reactio bekannt: Jede Aktion (jede Kraft) erzeugt eine gleich große Reaktion (eine gleich große Gegenkraft).
Diese drei Bewegungsgesetze, zusammen mit Angaben über die Eigenschaften von Kräften zwischen den Körpern wie beispielsweise der Gravitationskraft, bilden das Kernstück der klassischen Mechanik.
Soweit zur Prosa-Zusammenfassung. Jetzt wollen wir systematisch Definitionen und Konzepte entwickeln, um das Gesagte genauer beschreiben zu können – eben nicht nur mit Worten, sondern mit (einfachen) mathematischen Begriffen. Als erstes gehen wir daran, den Raum zu beschreiben, denn um ein Konzept wie Bewegung mathematisch zu erfassen, muss man angeben können, wo sich ein Objekt denn überhaupt befindet. Das grundlegende mathematische Modell für den Raum, in dem sich die klassische Physik abspielt, ist der euklidische Raum. Die Hilfsgrößen, mit denen sich Positionen von Objekten beschreiben lassen, sind Koordinaten in diesem Raum.
Euklidischer Raum und Koordinaten
Der zweidimensionale euklidische Raum dürfte den meisten Lesern aus dem Mathematikunterricht der Mittelstufe bekannt sein, wenn vielleicht auch unter anderem Namen: Dieser zweidimensionale Raum ist die Ebene, in der man ebene Geometrie betreiben und die Eigenschaften von Dreiecken und anderen geometrischen Figuren berechnen kann. Insbesondere gilt in diesem Raum für rechtwinklige Dreiecke der Satz des Pythagoras:
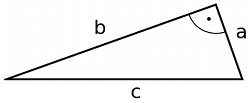
Ist c die Länge der Dreiecksseite gegenüber dem rechten Winkel, und sind a und b die Längen der anderen beiden Seiten, so gilt
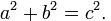
Wer die Geometrie der Ebene beherrscht, bringt beste Voraussetzungen mit, um sich im dreidimensionalen euklidischen Raum zurechtzufinden, denn in jeder Ebene in diesem Raum gelten die wohlbekannten Formeln der zweidimensionalen Geometrie.
Das dreidimensionale kartesische Koordinatensystem ist Stoff der Oberstufe: Jedem Punkt im Raum wird zur eindeutigen Identifikation ein Satz von drei Zahlen (x,y,z) zugeordnet. Sind die Werte von x,y,z bekannt, dann ist eindeutig festgelegt, von welchem Punkt die Rede ist. Umgekehrt gilt: Jedem Punkt im Raum entsprechen eindeutig bestimmte Werte für x, y, z. Definiert ist das Koordinatensystem durch drei Achsen, die senkrecht aufeinander stehen, alternativ durch die drei senkrecht auf diesen Achsen stehenden Ebenen durch den Achsenschnittpunkt. Ausschnitte aus den drei Ebenen und den drei Achsen sind hier farbcodiert skizziert:
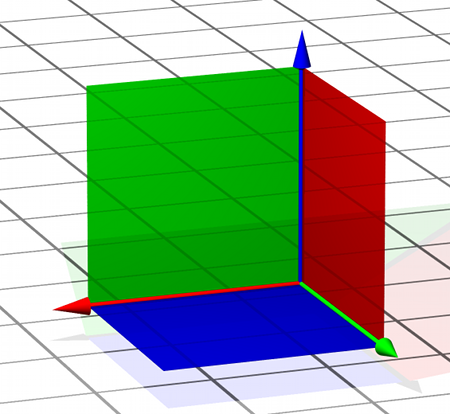
Nennen wir die grüne Achse die x-Achse (und die grüne Ebene die x-Ebene), die blaue Achse die y-Achse 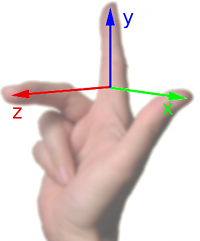 (die blaue Ebene die y-Ebene) und die rote Achse die z-Achse (rote Ebene = z-Ebene), dann haben wir die Basis eines so genannten rechtshändigen kartesischen Koordinatensystems; es heißt so, weil sich den Achsen in der rechts abgebildeten Weise Daumen, Zeige- und Mittelfinger der rechten Hand zuordnen lassen. Bei einem linkshändigen System zeigt die z-Achse in die Gegenrichtung; dann funktioniert die gleiche Zuordnung von Achsen zu Fingern mit der linken Hand. In allen Fällen gilt: Die Skizze kann nicht wiedergeben, dass die Achsen eigentlich unendlich lang, die Ebenen unendlich ausgedehnt sind.
(die blaue Ebene die y-Ebene) und die rote Achse die z-Achse (rote Ebene = z-Ebene), dann haben wir die Basis eines so genannten rechtshändigen kartesischen Koordinatensystems; es heißt so, weil sich den Achsen in der rechts abgebildeten Weise Daumen, Zeige- und Mittelfinger der rechten Hand zuordnen lassen. Bei einem linkshändigen System zeigt die z-Achse in die Gegenrichtung; dann funktioniert die gleiche Zuordnung von Achsen zu Fingern mit der linken Hand. In allen Fällen gilt: Die Skizze kann nicht wiedergeben, dass die Achsen eigentlich unendlich lang, die Ebenen unendlich ausgedehnt sind.
Sind Achsen bzw. Ebenen definiert, lässt sich direkt angeben, wie man einem beliebigen Punkt in diesem Raum drei Koordinatenwerte x,y,z zuordnen kann. Der kürzeste Abstand von diesem Punkt zur x-Ebene liefert den x-Koordinatenwert; in der folgenden Abbildung ist der Punkt als goldene Kugel dargestellt, und der x-Koordinatenwert ist die Länge der eingezeichneten grünlichen Strecke, die im Bild von der Kugel aus nach schräg links hinten läuft und die Kugel mit der grünen x-Wand verbindet:
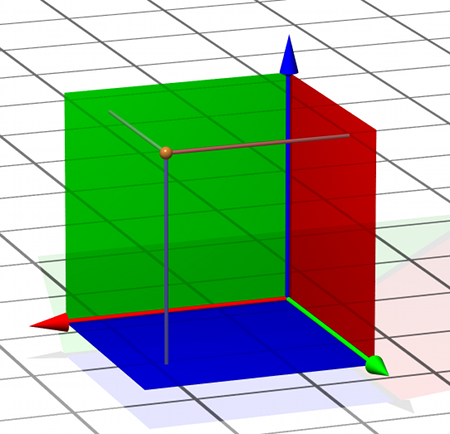
Der kürzeste Abstand der Kugel zur y-Ebene (bläuliche Strecke) liefert den y-Koordinatenwert, und analog verhält es sich mit z-Ebene und z-Koordinatenwert (rötliche Strecke).
Dass wir es mit einem euklidischen Raum zu tun haben, zeigt sich direkt daran, wie sich aus den Koordinatendifferenzen in x-, y- und z-Richtung zweier Raumpunkte der Abstand zwischen diesen Punkten ergibt. Sind x1, y1 und z1 die Koordinaten des ersten Raumpunktes und x2, y2 und z2 die des zweiten, dann ist der Abstand zwischen den beiden Punkten
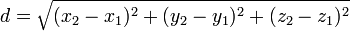
– das ist die dreidimensionale Version des Satzes des Pythagoras.
Es gibt unendlich viele verschiedene Möglichkeiten, ein kartesisches Koordinatensystem im euklidischen Raum zu definieren: Es gibt unendlich viele Raumpunkte, die man als Schnittpunkt der drei Achsen wählen kann, und unendlich viele Orientierungen für das Achsenkreuz. Die Koordinatenzuweisung ist also keineswegs eindeutig, ein Umstand, der im folgenden noch eine wichtige Rolle spielen wird.
Um eines der vielen möglichen Koordinatensysteme zu definieren, genügen vergleichsweise wenige Angaben. Eine Definitionsmöglichkeit besteht darin, drei durchnummerierte Punkte im Raum zu wählen und aus diesen drei Punkten nach den folgenden Regeln das kartesische Koordinatensystem zu konstruieren: Punkt 1 wählen wir als Koordinatennullpunkt und die Richtung der Verbindungsgerade von Punkt 1 und Punkt 2 als Richtung der x-Achse. Fällen wir das Lot von Punkt 3 auf die durch Punkt 1 und Punkt 2 definierte Gerade, erhalten wir die Richtung der y-Achse. Sind die Richtungen von x- und y-Achse bestimmt, dann bestimmen wir anhand der Rechte-Hand-Regel die Richtung der z-Achse, die senkrecht auf x- und y-Achse steht. Hier ist der Konstruktionsprozess grafisch dargestellt:

Neben den kartesischen Koordinaten gibt es noch weitere, äquivalente Arten von Koordinatensystemen. Ein wichtiges Beispiel sind die Kugelkoordinaten (sphärische Koordinaten), bei denen die Lage jedes Punktes durch eine Entfernung (die Entfernung des Punktes vom Nullpunkt) und zwei Winkel (zwischen der Verbindungsgeraden zum Nullpunkt und geeigneten Referenzebenen) angegeben wird. Diese anderen Koordinatensorten sollen uns hier erst einmal nicht näher beschäftigen. Stattdessen wollen wir jetzt die Brücke zwischen der Mathematik und der physikalischen Welt schlagen.
Physikalische Geometrie: Grundlagen
Euklidischer Raum und Koordinatensysteme sind mathematische Gebilde. Um sie als Modelle der physikalischen Wirklichkeit einzusetzen, muss man angeben, wie die mathematischen Konzepte in Mess- und Konstruktionsvorschriften umgesetzt werden sollen.
Für den zentralen Begriff eines Geradenabschnitts gibt es eine Reihe möglicher Entsprechungen. Beim Bau von Gebäuden wird gelegentlich noch eine straff gespannte Schnur eingesetzt, sei es als waagerechte Referenzgerade oder, mit einem Gewicht beschwert, als Lotstrecke. Auch für eine Kante eines Festkörpers lässt sich anhand einfacher Regeln definieren, wann sie gerade ist – so müssen sich zwei solche gerade Festkörperkanten beispielsweise an allen Punkten berühren, und dies auch, wenn man sie entlang der Kante verschiebt. Das Ergebnis ist ein Lineal.

Analog lässt sich definieren, wann z.B. zwei Metallplatten in guter Näherung Ausschnitte aus einer Ebene darstellen. Eine möglichst kleine Markierung auf solch einer Ebene oder der Kante eines Lineals – oder, allgemeiner, irgendeine besonders kleine Markierung – ist die physikalische Entsprechung eines Punkts.
Nächster Schritt ist die physikalische Definition von Längenmaßen. Urtyp eines Längenmaßes ist ein Maßstab, also ein Festkörper mit gerader Kante und gleichmäßigen, an der Kante aufgetragenen Unterteilungen. Eine Möglichkeit, solche gleichmäßigen Unterteilungen herzustellen, ist die physikalische Umsetzung von mathematischen Zirkelkonstruktionen: Ein Festkörper – etwa ein Stück Metall –, dessen einer Endpunkt fixiert ist und dessen anderer Endpunkt so präpariert ist, dass er auf einer Metallplatte Spuren hinterlässt, kann als Zirkel dienen. So lassen sich Konstruktionen wie die hier dargestellte zur Halbierung der Strecke, die A und B verbindet, in der Praxis umsetzen:
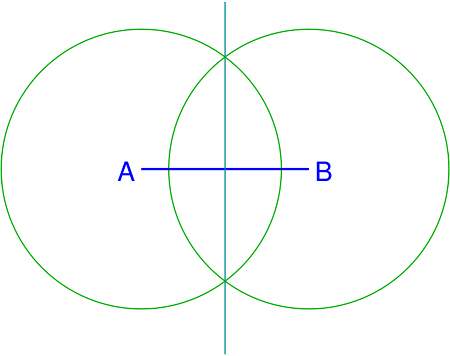
In Worten beschrieben: Man schlage mit dem Zirkel um A und um B zwei Kreise mit dem gleichen Radius; der Radius sollte groß genug sein, dass sich die Kreise in zwei Punkten schneiden. Der mit dem Lineal gezeichnete Ausschnitt der Verbindungsgerade der beiden Kreisschnittpunkte schneidet die A und B verbindende Strecke in einem Punkt. Dieser Punkt ist der Mittelpunkt der Strecke.
Aus Gerade, Abstand, Punkt und Ebene abgeleitete Konzepte lassen sich dann ebenfalls umsetzen: Ein Kreis mit gegebenem Radius als die Menge aller Punkte, die ein und denselben Abstand vom gemeinsamen Mittelpunkt haben; rechte Winkel und ihre Unterteilungen; Dreiecke oder andere Vielecke. Die Umsetzung wird niemals perfekt sein – ein noch so fein gearbeitetes Dreieck aus Aluminium hat nicht exakt die gleichen Eigenschaften wie ein mathematisches Dreieck; eine noch so kleine Markierung ist nicht exakt dasselbe wie ein Punkt. Entscheidend ist, dass für die in der wirklichen Welt definierten Entsprechungen der geometrischen Konzepte im Rahmen der Konstruktionsgenauigkeit die gleichen Gesetze gelten wie für ihre mathematischen Gegenstücke: Konstruiert man beispielsweise ein rechtwinkliges Dreieck aus Metall, so lässt sich abschätzen, um wieviel dessen Seitenlängen höchstens von denen eines idealen mathematischen Dreiecks abweichen sollten (Konstruktionsgenauigkeit). Für dieses Dreieck sollte in guter Näherung der Satz des Pythagoras gelten; etwaige Abweichungen sollten nur so groß sein, wie im Rahmen der gegebenen Konstruktionsgenauigkeit zu erwarten ist.
Physikalische Geometrie: Praxis
Die im vorangehenden Abschnitt angegebenen Zuordnungsvorschriften knüpfen direkt daran an, wie wir die geometrischen Konzepte im Mathematikunterricht lernen, wenn wir Dreiecke zeichnen, Konstruktionen mit Zirkel und Lineal ausführen und Strecken mit dem Lineal vermessen. Das ist ein großer Vorteil; von Nachteil ist, dass in der Praxis oft andere Mess- und Konstruktionsverfahren genauer und einfacher durchzuführen sind. Eben diese Verfahren nutzt auch die Physik für ihre “Geometrie der wirklichen Welt”. Damit wird der Anwendungsbereich des geometrischen Modells des Raums erweitert: Erweist sich etwa ein neues Verfahren zur Längenmessung im Rahmen der Messgenauigkeit als äquivalent zur fundamentalen Längenmessung mit unterteiltem Maßstab, dann bietet es sich an, auch die so gemessene Länge als Umsetzung der mathematisch-geometrischen Länge zu betrachten.
Für jede Methode, Geraden zu konstruieren und Abstände oder Winkel zu messen, lässt sich die Genauigkeit abschätzen. Zum einen gelingt dies durch methodenspezifische Untersuchungen, etwa zur Lichtbrechung in der Atmosphäre oder dem Biegeverhalten von Linealen aus bestimmten Materialien. Zum anderen kann man die Messungen ein und derselben Größe wiederholen und feststellen, wie weit die gemessenen Werte voneinander abweichen – in der Physik wie anderswo ein Standardverfahren zur Abschätzung zwar nicht systematischer Fehler, aber derjenigen Grenzen der Messgenauigkeit, die sich aus der Überlagerung einer Vielzahl winziger Störeinflüsse ergeben, wie sie bei jeder praktischen Messung auftreten.
 Für jeden Messbereich sollte man die jeweils genaueste und zuverlässigste Methode wählen, um geometrische Konzepte in die physikalische Welt zu übertragen. Bereits sehr alt ist eine Möglichkeit, Geradheit anders als über die Eigenschaften von Festkörpern zu definieren: In alltagsnahen Situationen läuft Licht im Rahmen der Messgenauigkeit im Vergleich mit Linealen auf Geradenabschnitten, breitet sich also geradlinig aus. Es liegt nahe, Licht zur Umsetzung des geometrischen Konzepts der Gerade zu verwenden, und dieses Vorgehen hat sich als höchst erfolgreich erwiesen. Licht-Geraden lassen sich durch bloßes Anvisieren definieren. Theodoliten (Bild rechts), mit denen sich Peilrichtungen mit hoher Präzision bestimmen lassen, gehören zu den genauesten verfügbaren Vermessungsinstrumenten. Mit ihnen lassen sich Distanzmessungen auf große Entfernungen ausdehnen, die durch das Aneinanderlegen von Linealen nicht oder zumindest nicht genau vermessbar wären.
Für jeden Messbereich sollte man die jeweils genaueste und zuverlässigste Methode wählen, um geometrische Konzepte in die physikalische Welt zu übertragen. Bereits sehr alt ist eine Möglichkeit, Geradheit anders als über die Eigenschaften von Festkörpern zu definieren: In alltagsnahen Situationen läuft Licht im Rahmen der Messgenauigkeit im Vergleich mit Linealen auf Geradenabschnitten, breitet sich also geradlinig aus. Es liegt nahe, Licht zur Umsetzung des geometrischen Konzepts der Gerade zu verwenden, und dieses Vorgehen hat sich als höchst erfolgreich erwiesen. Licht-Geraden lassen sich durch bloßes Anvisieren definieren. Theodoliten (Bild rechts), mit denen sich Peilrichtungen mit hoher Präzision bestimmen lassen, gehören zu den genauesten verfügbaren Vermessungsinstrumenten. Mit ihnen lassen sich Distanzmessungen auf große Entfernungen ausdehnen, die durch das Aneinanderlegen von Linealen nicht oder zumindest nicht genau vermessbar wären.
Bei solchen Vermessungen werden üblicher Weise mehr Winkel bestimmt, als für die Bestimmung der gesuchten Strecken bzw. Flächen notwendig sind. Das ermöglicht es, die gesuchten Größen auf mehr als eine Art zu berechnen und dann sowohl einen Mittelwert zu erhalten als auch eine Abschätzung der Genauigkeit der Messung vorzunehmen. Gleichzeitig zeigen solche Kontrollmessungen, mit welcher Genauigkeit die Lichtgeraden den Gesetzen der euklidischen Geometrie genügen. Der alte 10-DM-Schein, auf dessen Vorderseite Carl Friedrich Gauß (1777-1855) zu sehen war, zeigte auf der Rückseite nicht nur einen Sextanten, sondern in der rechten unteren Ecke auch ein Netz aus Dreiecken:

Hier ist der entsprechende Ausschnitt vergrößert abgebildet:
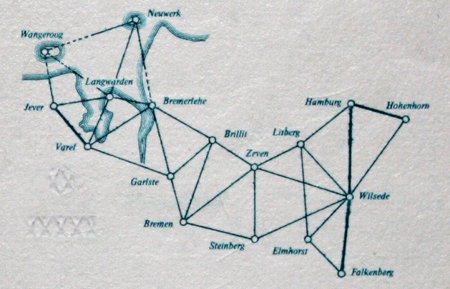
Es handelt sich um ein von Gauß bei der Vermessung des Königreichs Hannover angelegtes Vermessungsnetz.
Für die Längenmessung gibt es je nach Gültigkeitsbereich noch weitere genauere Verfahren, etwa Laser-Entfernungsmesser oder radarähnliche Verfahren. Bei letzteren wird aus der Verzögerung, mit der ein Radio- oder Lichtsignal vom Messpunkt zum Objekt läuft, dort reflektiert wird und wieder zum Messgerät zurück läuft, auf die Entfernung des Objekts geschlossen; für die Zwecke dieser Einführung müssen wir solche Messgeräte zunächst als “black box” betrachten, deren Genauigkeit wir zwar durch praktische Anwendung prüfen, deren Funktionsprinzip wir derzeit aber noch nicht nachvollziehen können, da wir die zur Beschreibung der Bewegung solcher Radio- oder Lichtsignale nötigen Konzepte noch nicht entwickelt haben. Moderne Theodoliten haben solch ein zusätzliches Abstandsmessverfahren oft gleich mit eingebaut und können damit Gebäude, aber z.B. auch Schiffs- oder Flugzeugrümpfe automatisch vermessen. Die Genauigkeit solcher Messungen ist enorm: bei zu vermessenden Bauteilen mit Gesamtausmaßen von um die 30 Metern liegt sie bei Bruchteilen eines Millimeters.
Bezugssysteme für den statischen Raum
Nach diesen Vorbereitungen sind wir zwar noch nicht soweit, dass wir sich bewegende Objekte oder sich verändernde Situationen beschreiben könnten — dazu fehlen Angaben, wie sich Ereignissen (etwa einem Ereignis wie “bewegtes Objekt A passiert den Raumpunkt X”) ein Zeitpunkt zuordnen lässt, wie sich also z.B. feststellen lässt, wann sich ein bewegtes Objekt wo befindet. Um solch eine Regel (äquivalent zu einer Definition der Gleichzeitigkeit) wird es im nächsten Teil der Einführung gehen.
Doch zumindest für statische Situationen – in denen sich nichts, oder zumindest nichts wesentliches, verändert, und in denen demnach z.B. alle Abstandsmessungen unabhängig vom Messzeitpunkt den gleichen Wert ergeben – lassen sich mit den bis hierhin eingeführten Zuordnungen kartesische Koordinatensysteme einführen. Ein solchermaßen in den wirklichen Raum eingebettetes Raumkoordinatensystem heißt Bezugssystem. Wenn wir betonen wollen, dass unser Bezugssystem nur für statische Situationen definiert ist, können wir es statisches Bezugssystem nennen.
Ein solches Bezugssystem ist schnell definiert – es reicht, dass wir drei Punkte im Raum benennen, und schon ist die Orientierung der kartesischen Koordinatenachsen entsprechend der oben angegebenen Regeln festgelegt. Dann müssen wir noch eine physikalische Längeneinheit definieren. Wir wählen die von 1960 bis 1983 gültige Definition des Meters als genau festgelegtes Vielfaches der Wellenlänge von Licht eines bestimmten atomaren Übergangs. (Warum die Zeiteinschränkung? 1983 wurde der Meter mit Bezug auf die Ausbreitungsgeschwindigkeit von Licht definiert; das greift den hier entwickelten Grundlagen vor – Ausbreitungsgeschwindigkeiten können wir überhaupt erst definieren, wenn wir eine Zeitkoordinate eingeführt haben.)
In vielen Situationen bietet sich eine bestimmte Definition schon aus praktischen Gründen an. Führt man Vermessungen mit einem Theodoliten durch, so kann es günstig sein, den Nullpunkt des Systems in den Schnittpunkt der beiden Drehachsen des Theodoliten zu legen, und diese Drehachsen dann gleich zur Definition der Achsenrichtungen zu verwenden. Was man am Theodolit direkt abliest, entspricht dann direkt den zwei Winkelangaben, die zu den drei Kugelkoordinaten eines Punktes gehören.

Die Abbildung zeigt nacheinander den Theodoliten samt angepeiltem Zielpunkt, die Peillinie, das mit dem Theodoliten verbundene Koordinatensystem (rote, grüne und blaue Achse) sowie die zwei Winkel des üblichen Kugelkoordinatensystems: α (Alpha, rot) als horizontal gemessenen Azimutwinkel zwischen Peillinie und roter Bezugsachse, und die Deklination δ (Delta, grün) als Winkel zwischen Peillinie und horizontaler Bezugsebene.
Die dritte Angabe, den Abstand des Ortes vom Koordinatennullpunkt, erhält man bei modernen Theodoliten, die als Laserstation ausgelegt sind, ebenfalls als direkte Messung: Solche Theodoliten können hochpräzise Laser-Entfernungsmessungen ausführen.
In anderen Situationen dagegen ist das Bezugssystem nicht so direkt an ein Messinstrument – und zum Teil noch nicht einmal an einen physisch markierten Koordinatennullpunkt – geknüpft. Vermisst man beispielsweise ein Gebäude und überträgt die Messwerte in ein Computermodell des Gebäudes, wie es heutzutage zu den Standardwerkzeugen der Architekten gehört, dann ist das Koordinatensystem des Computermodells ein vollkommen legitimes Bezugssystem – allerdings nicht eines, dessen Nullpunkt und Achsenrichtungen notwendiger Weise direkt im Gelände markiert wären.
Eine weitere konkrete Umsetzung eines kartesischen Koordinatensystems – wenn auch nur für einen kleinen Ausschnitt aus dem gesamten Raum – bietet eine Maschine wie diese hier, die in der Feinmechanikwerkstatt des Max-Planck-Instituts für Astronomie steht:

Die Maschine hat einen Arm, an dessen Spitze ein Zeiger sitzt.  Eine elektronische Anzeige gibt die aktuellen x,y,z-Koordinaten der Zeigerspitze an, bezogen auf ein durch die Maschine definiertes Koordinatensystem. Rechts ist ein Ausschnitt des Bildes zu sehen, der die Zeigerspitze zeigt: die kleine rote Kugel, die hier gerade auf einem eingespannten Aluminiumwerkstück aufliegt; geführt wird die Scannerspitze an dem am oberen Bildrand sichtbaren Griff (mit rotem Ring). Die Koordinaten jedes gerade angefahrenen Punktes lassen sich durch einfaches Klicken im Computer festhalten. Auf diese Weise lässt sich ein Werkstück hochgenau dreidimensional vermessen, indem man die Zeigerspitze nach und nach an alle die Form definierenden Punkte des Werkstücks führt und die betreffenden Koordinatenwerte x,y,z festhält.
Eine elektronische Anzeige gibt die aktuellen x,y,z-Koordinaten der Zeigerspitze an, bezogen auf ein durch die Maschine definiertes Koordinatensystem. Rechts ist ein Ausschnitt des Bildes zu sehen, der die Zeigerspitze zeigt: die kleine rote Kugel, die hier gerade auf einem eingespannten Aluminiumwerkstück aufliegt; geführt wird die Scannerspitze an dem am oberen Bildrand sichtbaren Griff (mit rotem Ring). Die Koordinaten jedes gerade angefahrenen Punktes lassen sich durch einfaches Klicken im Computer festhalten. Auf diese Weise lässt sich ein Werkstück hochgenau dreidimensional vermessen, indem man die Zeigerspitze nach und nach an alle die Form definierenden Punkte des Werkstücks führt und die betreffenden Koordinatenwerte x,y,z festhält.
Praktisch oder unpraktisch, konkret oder abstrakt: Es gibt viele verschiedene Arten und Weisen, im physikalischen Raum Koordinaten zu definieren. Und solange die Definition eines bestimmten Koordinatensystem nur in der Tat jedem Raumpunkt – oder zumindest jedem Punkt eines bestimmten Bereichs im Raum – eindeutig Koordinatenwerte x,y,z zuordnet, erfüllt es seinen Zweck: Es stellt einen Bezug her zwischen der physikalischen Welt und einem mathematischen Modell des dreidimensionalen Raums, nämlich dem euklidischen Raum.
Koordinatenwillkür und Transformationen
In diesem Abschnitt möchte ich einige allgemeine Eigenschaften der kartesischen Koordinatensysteme, über die wir unsere statischen Bezugssysteme definiert haben, Revue passieren lassen. Er ist etwas mathematischer als die vorangehenden Abschnitte, kann von ungeduldigen Lesern, die möglichst bald zu relativistischen Effekten wie Zeitdilatation oder Lorentzkontraktion vordringen möchten, übersprungen werden, bietet aber wichtige Informationen zum mathematischen Hintergrund des hier Gesagten (und des mathematischen Hintergrunds der nachfolgenden Ausführungen zur Speziellen Relativitätstheorie).
Wie wir gesehen haben, gibt es viele verschiedene Möglichkeiten, einer statischen Situation kartesische Koordinaten zuzuordnen. Im allgemeinen werden sich dabei die Koordinatenwerte, die zu ein und demselben Raumpunkt gehören, von Koordinatensystem zu Koordinatensystem unterscheiden. Bestimmte Verknüpfungen der Koordinatenwerte dagegen ergeben Größen, die in jedem Koordinatensystem den gleichen Wert haben. Das gilt insbesondere für den durch Koordinatendifferenzen ausgedrückten Abstand zwischen Raumpunkten,
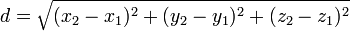
und für aus solchen Abstandswerten zusammengesetzte Größen. Das ist nicht überraschend, denn es spiegelt wieder, dass all die verschiedenen Koordinatensysteme die zugrunde liegende Geometrie, nämlich die Abstände zwischen Raumpunkten oder auch die Winkel zwischen Geraden, die mehrere Punkte verbinden, zutreffend wiedergeben.
Aus Sicht der Geometrie sind die vielen Koordinatensysteme damit äquivalent — es ist egal, welches davon wir wählen; die geometrischen Beziehungen werden in jedem davon korrekt wiedergegeben. Umgekehrt haftet damit jeder Wahl eines Koordinatensystems etwas Willkürliches an. Anstatt in dem gewählten System lässt sich dieselbe Situation genau so gut in einem der unendlich vielen anderen Systeme beschreiben.
Der Übergang von einem möglichen statischen Koordinatensystem zu einem zweiten lässt sich als genau definierte Operation wiedergegeben, nämlich als Kombination von der relativen Lage der beiden Systeme abhängigen Rotation (einer Drehung des Koordinatensystems im Raum), welche die Achsen des ersten Koordinatensystems so dreht, dass sie anschließend parallel zu den Achsen des zweiten Systems sind, und einer nur vom Abstand der beiden Koordinatennullpunkte abhängigen Translation (einer Verschiebung des Koordinatensystems um eine bestimmte Distanz in eine bestimmte Richtung), durch deren Ausführung der Nullpunkt des ersten Koordinatensystems zum Nullpunkt des zweiten Koordinatensystems verschoben wird. Wendet man diese Operation auf das erste Koordinatensystem an, dann ist das Ergebnis das zweite Koordinatensystem. Hier ist der Prozess beispielhaft dargestellt; gezeigt wird skizzenhaft, wie ein Koordinatenkreuz in ein anderes überführt wird:
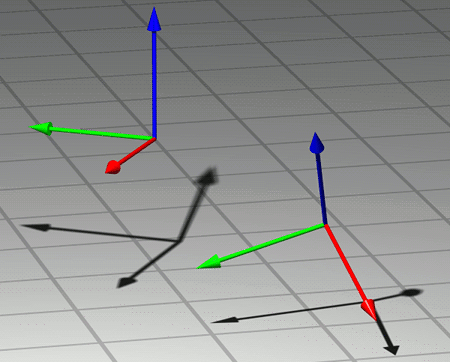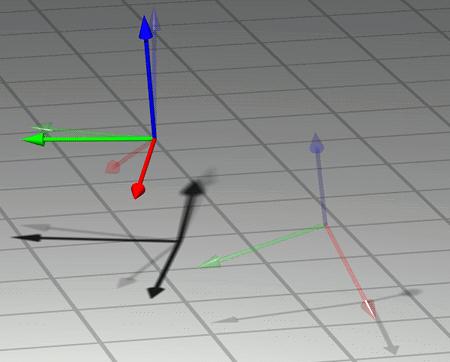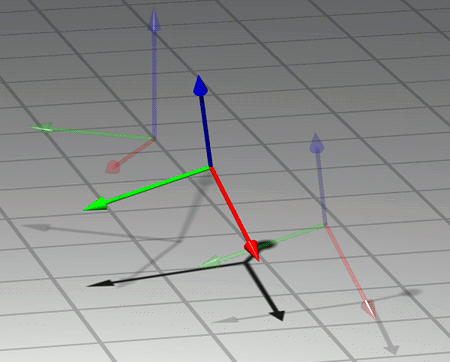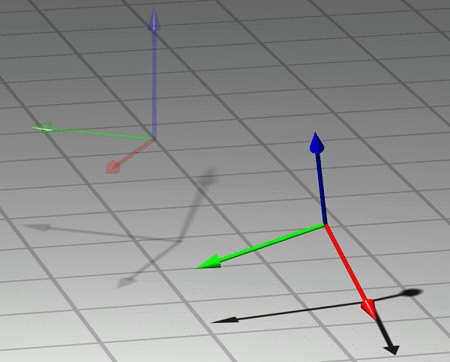
Führt man zwei solche Operationen hintereinander aus (und überführt damit z.B. Koordinatensystem A in Koordinatensystem B und anschließend Koordinatensystem B in Koordinatensystem C), entspricht die Kombination wieder einer Operation der gleichen Art, nämlich einer Rotation und einer Translation (derjenigen Kombination aus Rotation und Translation nämlich, die das Koordinatensystem A direkt in das Koordinatensystem C überführt). Auch längere “Ketten” von Operationen sind eindeutig definiert, sobald man nur jede der Teiloperationen angibt und sagt, in welcher Reihenfolge die Teiloperationen ausgeführt werden. Für jede Operation gibt es eine eindeutig bestimmte “Anti-Operation”, welche die erste Operation rückgängig macht, sprich: Gibt es eine Operation, die das Koordinatensystem A in das System B überführt, so existiert immer auch eine Operation, die B in A überführt. Mathematisch gesprochen bilden Operationen mit diesen Eigenschaften eine so genannte Gruppe.
Die Gruppe der Operationen, welche die verschiedenen äquivalenten Koordinatensysteme ineinander überführen, heißt unter Mathematikern “Symmetriegruppe des [dreidimensionalen] euklidischen Raums” oder “Gruppe der Bewegungen”, abgekürzt ISO(3) oder E(3).
Interessanterweise lässt sich die Geometrie des euklidischen Raums direkt aus den Eigenschaften der Gruppe ISO(3) rekonstruieren. Vereinfacht gesagt: Die Eigenschaften der Operationen definieren die Invarianten der Gruppe, also diejenigen Größen, die bei der Operation unverändert bleiben. Diese Invarianten sind Abstände in dem durch die Koordinatensysteme definierten Raum (und daraus abgeleitete Größen), und damit die grundlegenden Elemente der euklidischen Geometrie des Raums.
Die in diesem letzten Abschnitt angesprochenen allgemeineren Eigenschaften werden uns in dieser Einführung noch weiter begleiten, und sie spielen auch in anderen Teilen der Physik eine wichtige Rolle. Allgemein haben wir es mit einem zugrunde liegenden mathematischen Gebilde zu tun (hier: mit dem euklidischen Raum), das sich nur durch Wahl von Koordinaten (hier: eines kartesischen Koordinatensystems) allgemein beschreiben lässt. Doch jede konkrete Koordinatenwahl ist willkürlich; es gibt unendlich viele gleichwertige Möglichkeiten. Die verschiedenen Wahlmöglichkeiten lassen sich durch Transformationen (hier: die Rotation-plus-Translation) ineinander überführen. Die Transformationen bilden eine Gruppe (hier die ISO(3)); die Invarianten der Gruppe wiederum sind eine Möglichkeit, das zugrunde liegende mathematische Gebilde zu charakterisieren.
3. Nicht auf der Hauptseite veröffentlichte Kommentare
…unterteilt in die Abteilungen Gemischte Kommentare und Diskussion mit J. Lopez über persönliche Angriffe etc..
Kommentar von Manuel Krüger
Sehr geehrter Herr Dr. Pössel,
ich weiß, dass ich hier nun mitten in einen Dialog platze, aber wo man hier doch einen Mann vom Fach hat, hätte ich da mal eine paar recht einfache Fragen.
In 10km von der Erde entfernt entsteht ein Myon, mit einer Geschwindigkeit von 0,994c. Von der Erde aus gibt es ein Maßband das weit in die Atmosphäre reicht. Dort oben bei 10km entsteht nun das Myon zum Zeitpunkt t0.
Bis hier herrscht auch noch Einigkeit. Wir haben nun zwei Bezugsysteme, das in dem die Erde ruht und das Myon sich mit 0,994c bewegt, und das System in dem das Myon ruht und sich die Erde mit 0,994c bewegt. Das Maßband der Erde ist im Erdesystem nicht bewegt und somit in diesem natürlich nicht kontrahiert.
Nun gibt es im System des Myons auch ein solches Maßband, das bis zur Erde reicht. Dieses ist nun im System des Myons nicht bewegt und zeigt dort also seine Ruhelänge.
Die erste Frage ist nun, sieht man als Beobachter im System des Myons am Ende des eigenen Maßbandes die Erde bei 10km?
Zweite Frage, ist das der Zeitpunkt t0?
Dritte Frage, das Maßband der Erde mit seinen 10km Ruhelänge ist im System des Myons bewegt. Dort sollte es nun Aufgrund der LK nur mit 1,1km Länge gemessen werden. Ist nun das Ende (die 10km Markierung) dieses Maßbandes das ja im System Erde ruht, im System des Myons dort am Punkt 8,9km des eigenen Maßbandes?
Man liest immer, dass die Erde im System des Myons aufgrund der Geschwindigkeit verkürzt gemessen wird. Beide Systeme sind doch gleichwertig. Beide haben ein Maßband von 10km das im eigenen System ruht. Wenn nun ein Beobachter von der Erde das Myon in einer Entfernung von 10km misst, dann sollte das Myon doch auch die Erde in einer Entfernung von 10km messen.
Im meinem System sind Entfernungen doch Ruhelängen, verkürzt messe ich doch nur die Längen, die sich zu mir bewegen. Das bedeutet, Anfang- und Endpunkt der Länge bewegen sich relativ zu dem Nullpunkt meines Systems, aber haben zueinander keine Geschwindigkeit.
Ich würde einfach mal gerne hören, wie Sie das beschreiben.
Ein frohes Fest und viel Erfolg bei dieser Seite hier, wünscht Ihnen
Manuel Krüger
Kommentar von MP: Ich bitte um Verständnis, das ich an dieser Stelle nicht vorgreifen möchte. Nur Geduld, wenn alles gut geht, kommen wir mit der Zeit auch zu den Fragen, die Sie hier ansprechen.
Kommentar von W. Lange, Einstein-Lorentz-Transformatiion, 15.4.2011
Sehr geehrter Herr Dr.Pössel,
sehr geehrter Herr Bergner,
es wird Zeit, Sie an meinen letzten Satz in dem Beitrag vom 16.12.2010 zu erinnern. Es gab dazu einige Bemerkungen, aber den Satz hat wohl niemand gelesen. Ich habe versucht, dem toten Herrn Einstein in den “Annalen der Physik” zu antworten, aber der verantwortliche Professor glaubt an Einstein (wie an den Gott der Juden, Christen und Mohammedaner) und war nicht bereit, meinen Artikel zu veröffentlichen. Die abschlägige Antwort kam bereits nach 19 min.
Deshalb lade ich alle Befürworter und Kritiker zum Besuch meiner Web-Seite ein: http://www.wwlange.de
Auf Ihre kritischen Anworten freue ich mich schon.
W.Lange
Kommentar von marko, Diskussionen mit unorthodoxen Kritikern, 20.04.2011 | 14:00
und Cranks, die etablierten Theorien in Mathematik und Physik widersprechen, z.B. Kritiker der Relativitätstheorie,
missverstehen diese Theorien in der Regel,zeigen fast immer einen Mangel an mathematischen und physikalisch-technischen Fertigkeiten,
sind häufig nicht willens oder in der Lage, die übliche Notation und Terminologie zu benutzen,
missachten feine Unterschiede, die zum Verständnis etablierter Theorien notwendig sind.
Cranks kokettieren häufig mit einer Missachtung für Bildung. Beispielsweise argumentieren sie, dass ein naturwissenschaftliches Studium für ihr Spezialgebiet nicht nur unnötig sei, um die “Wahrheit” zu erkennen, sondern sogar schädlich, weil man dort nur festgefahrene Wege lerne, unkonventionelle Sichtweisen “unterdrückt” würden, usw. Dennoch zeigen Cranks häufig eine Vorliebe für promovierte oder habilitierte Personen.
Antwort von MP: Das gehört wohl eher zu diesem älteren Blogeintrag von mir.
Kommentar von Wolfgang Lange, Allgemein, 6.5.2011 | 00:07
Danke Herr Dr. Pössel,
dass Sie meinen Beitrag vom 15.4.2011 sofort in den Hintergrund verschoben haben.
Dann kann man ihn auch nicht zwischen dem 1.4. und 30.4. d.J. finden. Sieht so Relativität aus?
M.f.G.
W.Lange
Kommentar von J. Lopez, Ein Scherz?, 6.5.2011 | 14:53
@ Dr. Markus Pössel:
25.04.11 Zitat Dr. Markus Pössel:
“Und siehe da, in jener Diskussion haben Sie genau die Art von Kommunika-tionsproblemen, vor denen ich Sie ob Ihrer “Privatsprache” gewarnt hatte.“
Ich schlage vor, dass wir die Thematik des Verständnisses meiner „Privatsprache“ verlassen, und dass wir uns dem Verständnis der “Privatsprache“ Einsteins widmen – schließlich heißt dieses Blog-Experiment auch „Einstein verstehen“.
Einstein hat in seiner Veröffentlichung 1905 konkrete Messverfahren für die Messung der Länge eines Stabes beschrieben – seine ganze Theorie basiert ja auf einem bestimmten Längenmessverfahren – wir sind also damit voll im Thema des Teils I. Er schreibt zum Beispiel Seiten 895-896:
Zitat Albert Einstein:
“Es sei ein ruhender starrer Stab gegeben; derselbe besitze, mit einem ebenfalls ruhenden Maßstabe gemessen, die Länge l.
[…]
Wir fragen nun nach der Länge des bewegten Stabes, welche wir uns durch folgende zwei Operationen ermittelt denken:
a) Der Beobachter bewegt sich samt dem vorher genannten Maßstabe mit dem auszumessenden Stabe und mißt direkt durch Anlegen des Maßstabes die Länge des Stabes, ebenso, wie wenn sich auszumessender Stab, Beobachter und Maßstab in Ruhe befänden.“
Das Meßverfahren für die Messung der Länge des ruhenden Stabes, das Einstein in seinem ersten Satz beschreibt, verstehe ich sowohl sprachlich als auch von der Vorstellung der konkreten Handlung sehr gut: Ein ruhender Beobachter misst einen ruhenden Stab durch Anlegen eines ruhenden Maßstabes. Ich habe hier kein Verständnisproblem.
Das Meßfahren, das Einstein als “Operation a“ beschreibt, bereitet mir dagegen sehr große Verständnisprobleme. Ich verstehe den Satz so, dass ein Beobachter auch durch direktes Anlegen des Maßstabes die Länge des bewegten Stabes messen soll, und zwar so, als ob Beobachter und Maßstab sich relativ zueinander in Ruhe befänden. Dieser Zustand der relativen Ruhe zwischen Beobachter und Maßstab beim direkten Anlegen des Maßstabes auf dem Stab kann nur bewerkstelligt werden, wenn der Beobachter sich mit gleicher Geschwindigkeit neben dem bewegten Stab bewegt. Man solle also die Länge des bewegten Stabes so messen, dass man neben dem Stab läuft oder fährt und den Maßstab direkt anlegt.
Dieses Meßfahren scheint mir sehr abenteuerlich, um nicht zu sagen äußerst skurril. Habe ich da irgendetwas sprachlich nicht verstanden oder soll es sich vielleicht um einen Scherz handeln? Einstein hatte ja bekanntlich einen ausgeprägten Sinn für Humor, was mir persönlich ganz gut gefällt.
Aber konnte man sich 1905 in der renommierten und seriösen wissenschaftlichen Zeitschrift „Annalen der Physik“ überhaupt so einen Scherz erlauben?
Was meinen Sie?
Viele Grüße
Jocelyne Lopez
Antwort von MP: Bei Orts- und Längenbestimmungen von bewegten Objekten in der Speziellen Relativitätstheorie sind wir hier noch lange noch nicht. Bitte nicht vorgreifen!
Kommentar von Manuel Krüger, @Jocelyne Lopez – Scherz, 6.5.2011 | 18:19
„Zitat Albert Einstein: a) Der Beobachter bewegt sich samt dem vorher genannten Maßstabe mit dem auszumessenden Stabe und misst direkt durch Anlegen des Maßstabes die Länge des Stabes, ebenso, wie wenn sich auszumessender Stab, Beobachter und Maßstab in Ruhe befänden.“
Das Messverfahren für die Messung des ruhenden Stabes, das Einstein in seinem ersten Satz beschreibt, verstehe ich sowohl sprachlich als auch von der Vorstellung der konkreten Handlung sehr gut: Ein ruhender Beobachter misst einen ruhenden Stab durch Anlegen eines ruhenden Maßstabes. Ich habe hier kein Verständnisproblem.“
Verwunderlich…
„Das Messverfahren, das Einstein als “Operation a“ beschreibt, bereitet mir dagegen sehr große Verständnisprobleme.“
Nicht verwunderlich…
„Ich verstehe den Satz so, dass ein Beobachter auch durch direktes Anlegen des Maßstabes die Länge des bewegten Stabes messen soll, und zwar so, als ob Beobachter und Maßstab sich relativ zueinander in Ruhe befänden. Dieser Zustand der relativen Ruhe zwischen Beobachter und Maßstab beim direkten Anlegen des Maßstabes auf dem Stab kann nur bewerkstelligt werden, wenn der Beobachter sich mit gleicher Geschwindigkeit neben dem bewegten Stab bewegt. Man solle also die Länge des bewegten Stabes so messen, dass man neben dem Stab läuft oder fährt und den Maßstab direkt anlegt.“
Liebe Frau Lopez, beginnen wir mal wieder beim klassischen Relativitätsprinzip, das sie ja neben der SRT auch für falsch halten. Viele ihrer „Missverständnisse“ liegen ja darin begründet. Hier hat Britta meine Erklärung für sie noch mal ganz einfach zusammengefasst:
http://www.mahag.com/…c.php?f=7&t=332#p19764
Auch hier kann man wieder erkennen, wo ihr Problem liegt:
http://www.mahag.com/…t=330&start=210#p19806
Ernst hatte neben vielen anderen mehrfach versucht, ihnen erstmal nur das klassische Relativitätsprinzip zu erklären. Wie alle anderen, war das vergeblich, wie man hier sieht:
Sie schreiben ja selber in ihrem Blog: http://www.jocelyne-lopez.de/…falsch-eingesetzt/ und wie immer im Mahagforum: http://www.mahag.com/…iewtopic.php?f=7&t=332
„Natürlich kann man am laufenden Band in der Physik den Zustand der Ruhe von der Zustand der Bewegung unterscheiden, man braucht nur ein Bezugssystem zu haben: das Bezugssystem des Beobachters, der die Messung vornimmt.
Wenn ich in einem Zug mit verstopften Ohren, geschlossenen Fenstern und extrem weichen Sitzen sitze kann ich nicht als Beobachter fungieren, weil ich durch meinen Sinnesapparat keinen Zugang zu einem Bezugssystem oder einem Bezugspunkt habe. Man kann nun mal ohne Sinneseindrücke und ohne Bezugssystem keinen Zustand der Ruhe oder der Bewegung feststellen, das habe schon mal in meinem vorherigen Beitrag dargelegt, als Du die Objekte ohne Beobachter und ohne Bezugssystem am liebsten allein im Universum versetzen wolltest, damit das Relativitätsprinzip zur Geltung kommt… Ohne Beobachter und Bezugssystem kann man eben weder Zustand der Ruhe oder der Bewegung feststellen, noch irgendeine Messung durchführen, kein Wunder.
Jeder beliebigen Beobachter im Zug oder außerhalb des Zuges, der jedoch Zugang zu einem Bezugssystem hat, weil er sehen, hören und fühlen kann, ist aber jederzeit in der Lage, den Zustand der Ruhe oder der Bewegung des Zuges festzustellen, Relativitätsprinzip hin oder her.
Es stimmt also überhaupt nicht, dass man prinzipiell nicht den Zustand der Ruhe oder der Bewegung feststellen kann. Das machen Menschen jede Sekunde millionenfach seit ihrer Geburt, das machen auch Wissenschaftler und Techniker tagtäglich.
[…]
Sei mir nicht böse, Ernst, aber ich entnehme Deinen Beiträgen, dass Du das Wesen und vor allem die Grenzen und den Gültigkeitsbereich des Relativitätsprinzips in der Physik immer noch nicht nachvollziehen kannst.
Andere qualifizierte Autoren können es durchaus, wie ich es zitiert habe. Ist auch nicht besonders verwunderlich, es gibt gelegentlich eine ausgesprochene hartnäckige “Betriebsblindheit” unter den Fachleuten und aufgrund der ziemlichen Bedeutungslosigkeit dieses Prinzips in der Alltagsphysik und in der Technologie, ist es auch nicht weiter störend. Auch in der theoretischen Physik ist dieses Prinzip nicht von herausragender Bedeutung, außer für die Spezielle Relativitätstheorie, die es als 1. Postulat übernommen hat. Aber bekanntlich ist die Spezielle Relativitätstheorie selbst physikalisch wirklichkeitsfremd, nichtssagend und irrelevant.“
Und wie immer, schieben sie ihr „Missverständnis“ dem Gegenüber zu, in diesem Fall eben Ernst. Das sie es sind, die was nicht nachvollziehen kann, kommt ihnen nicht in den Sinn. Da versteht eben der Ingenieur und der Physiker die Dinge einfach nicht richtig, zum Glück sind sie ja zur Stelle um das klarzustellen.
Selbst Kritik an ihrem „Verständnis“ aus den eingen Reihen der Kritiker, prallt an ihnen ab. Sie irren eben nie…
Hier wird das deutlich:
http://www.mahag.com/…t=330&start=130#p19638
Neben Ernst hast auch Chief als Kritik dazu geschrieben: Wenn von zwei Uhren eine relativ zu der anderen bewegt wird dann ist auch die andere relativ zu der ersten genauso bewegt. Das hat Ernst vergeblich versucht Frau Lopez klar zu machen (offensichtlich versteht es mancher einer hier nicht).
Und ich könnte hier noch 20 weitere Beiträge verlinken, in denen man ihnen versuchst hat, erstmal die einfach klassisch Physik, einfach das klassische Relativitätsprinzip beizubringen, es ist vergeblich.
Somit ist es auch nicht möglich, dass sie die SRT begreifen können, für sie ist auch kinetische Energie keine relative Sache, sondern eine intrinsische Eigenschaft eines Körpers.
Kein Wunder, das sie somit die Aussage von Einstein nicht verstehen, wobei das Problem nicht nur darauf zurückzuführen ist, das sie das Relativitätsprinzip leugnen, sondern auch, das sie die Aussage selber nicht in ihrer Bedeutung verstehen.
Eben wegen dem Relativitätsprinzip, gibt es keine „Bewegung“ zu dem zu messenden Stab, wenn sich mit gleicher Geschwindigkeit daneben her bewegen. Sie haben immer noch das Bild im Kopf, sie können durch den Äther rennen, sie hätten eine „Eigengeschwindigkeit“ wie sie ja auch oft schreiben. Ein Körper hat keine Eigengeschwindigkeit, eine Geschwindigkeit ist immer eine Relation.
Es macht also nur Sinn, wenn der Beobachter eben nicht mit der „gleichen“ Geschwindigkeit wie der zu messende Stab bewegt ist.
Ich spare mir hier nun aber, ihnen das zum tausendsten Mal vergeblich zu erklären, und den Lesern hier im Blog dürfe das Relativitätsprinzip sicher keine solchen Probleme bereiten.
Fakt ist aber, wenn man sich weigert, das Relativitätsprinzip zu verstehen, wenn man hier also nicht nur eine eigene Sprache spricht, Begriffe umdeutet, sondern auch die Grundlagen der Physik einfach über Bord wirft, und dann damit an die SRT geht, dann kann es nur zu „Missverständnissen“ führen
„Dieses Messverfahren scheint mir sehr abenteuerlich, um nicht zu sagen äußerst skurril. Habe ich da irgendetwas sprachlich nicht verstanden oder soll es sich vielleicht um einen Scherz handeln? Einstein hatte ja bekanntlich einen ausgeprägten Sinn für Humor, was mir persönlich ganz gut gefällt. Aber konnte man sich 1905 in der renommierten und seriösen wissenschaftlichen Zeitschrift „Annalen der Physik“ überhaupt so einen Scherz erlauben?“
Der einzige Scherz, denn ich erkenne ist, das sie meinen sie können sich zur SRT in irgendeiner Weise qualitativ äußern, oder gar an einem Dialog in einem Blog dazu etwas sinnvolles sagen.
Mein wirklich gut gemeinter Rat, schweigen sie lieber, bis sie die Grundlagen der Physik verstehen, ich habe auch noch nie einen Menschen gesehen, der sich öffentlich so demontiert, und seine Unfähigkeit in Szene setzt.
Frau Lopez, sie tunen sich wirklich keinen Gefallen, wenn sie hier schreiben, man lässt sie hier nur schreiben, weil sie sich selber so wunderbar zerlegen. Herr Pössel muss dazu gar nichts mehr schreiben, jeder kann erkennen, dass sie nicht den Hauch einen Schimmer von den Dingen, über die sie schreiben, an Ahnung haben.
Sie machen sich öffentlich zu einer Witzfigur, lernen sie bitte erst die Grundlagen, bevor sie hier sich zu physikalischen Fragen äußern.
Und ich habe mir einige Links verkniffen, um es nicht noch schlimmer für sie zu machen.
Antwort von MP: Siehe mein letzter Kommentar – bitte nicht vorgreifen; soweit sind wir noch nicht!
Kommentar von Harald, Ohmsches Gesetz, 14.05.2011 | 12:30
Frau Lopez,
Ihr Blogeintrag vom 13.5.2011: bitte korrigieren Sie folgende Falschaussage:
“Das ohmsche Gesetz gilt nicht bei Wechselspannung.”
Das ist falsch und zeugt von mangelnder Sachkenntnis. Es ist unter Fachleuten allgemein bekannt, dass bei Wechselspannung mit realen und imaginären Anteilen gerechnet wird.
Kommentar von MP: Ich verstehe ja Ihre Frustration, dass Frau Lopez in Ihrem Blog keinerlei Kommentare zulässt, aber hier bitte im Interesse der Mitleser bitte nur Kommentare direkt zu dem Blogeintrag “Einstein verstehen Teil I” einstellen.
Kommentar von Harald, Ohmsches Gesetz Teil 2, 15.05.2011 | 10:08
Frau Lopez,
leider ist es immer noch nicht möglich, auf Ihrem Blog zu kommentieren, daher weise ich Sie hier auf einen weiteren Fehler im Beitrag vom 14.Mai 2011 hin.
Zitat Anfang
“Auch wenn ich den Strom so stark erhöhe, daß aufgrund der Verlustwärme die Schmelztemperatur des Konstantan-Drahtes überschritten wird?
Dann natürlich nicht! “
Zitat Ende
Natürlich gilt auch hier das ohmsche Gesetz, nur geht der Widerstand gegen Unendlich.
Entschuldigen Sie bitte die Aussage, aber in Ihrem Blog kritisieren Sie etwas, was Sie gar nicht verstanden haben. Das Ohmsche Gesetz verliert nicht dadurch seinen Wert, dass es keinen idealen ohmschen Widerstand gibt.
Ihr Blogbeitrag verliert so allerdings jeglichen Wert, daher noch einmal meine Anregung, ihn zu überarbeiten.
Kommentar von MP: Siehe meinen vorangehenden Kommentar – dass Frau Lopez in ihrem eigenen Blog keine Kommentare zulässt, mag frustrierend sein, aber hier ist kein geeigneter Ersatz-Diskussionsort.
3.2 Diskussion mit J. Lopez u.a. über persönliche Angriffe etc.
Kommentar von Jocelyne Lopez, Geht um meinen Blog oder um Ihren Blog?, 22.5.2011 | 11:59
@ Dr. Markus Pössel:
“Auch bei jenem Blogtext werden dann selbstverständlich Kommentare und Nachfragen zugelassen sein. Das gehört bei einem richtigen Blog einfach dazu; klar gibt es immer auch Trolle, die die angebotene Gelegenheit zum offenen Austausch missbrauchen, aber das muss eine gesunde Diskussionskultur bis zu einem gewissen Grade aushalten können. Probieren Sie’s doch ruhig mal selbst aus, Frau Lopez; gehe ich recht in der Annahme, dass die Kommentarfunktion in Ihrem eigenen Blog nach wie vor ganz ausgeschaltet ist, dort also überhaupt keine Kommentare möglich sind?“
Was interessiert Sie eigentlich, ob die Kommentarfunktion in meinem Blog eingeschaltet oder ausgeschaltet bzw. einzuschalten oder auszuschalten ist? Geht es hier um mein Blog oder um Ihren Blog??
[MP: OK, offenbar stoße ich hier an eine Längenbeschränkung. Anfrage an die Technik ist abgeschickt…]

