Das Meereis-Minimum 2011
BLOG: KlimaLounge

Die Eisfläche in der Arktis bewegt sich nahe am Rekordminimum (siehe Grafik), und die Schmelzsaison ist noch nicht vorbei. Ein Gastbeitrag vom Hamburger Meereisexperten Lars Kaleschke.
Die Eisfläche auf dem arktischen Ozean ist in diesen Tagen so weit zusammengeschrumpft wie im bisherigen Rekordminimum im September 2007 (Abb. 1). Das National Snow and Ice Data Center der USA vermeldete vorgestern, dass offenbar die Nordwest- und die Nordostpassage gleichzeitig offen sind – was erstmals im Jahr 2008 der Fall war (KlimaLounge berichtete).
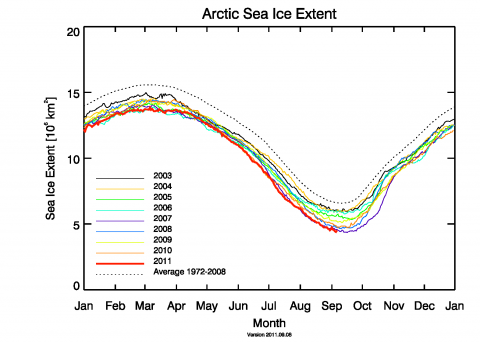
Abb. 1: Eisausdehnung im arktischen Ozean im Verlauf der letzten Jahre (nach Auswertung von Satellitendaten der Universität Bremen)
Was gibt es zum September-Minimum in diesem Jahr zu sagen? Im Jahr 2007 gab es ein überraschendes Rekordminimum, das weit unterhalb des langjährigen Klimamittelwertes lag. In diesem Jahr erreichen wir einen Wert, der dem von 2007 zumindest nahe kommt. Ob ein neues Rekordminimum erreicht wird oder nicht, schon heute können wir aus den Daten einige interessante Schlussfolgerungen ziehen:
- 2007 und 2011 sind keine statistischen Ausreißer, die nur auf ganz besondere Wettterlagen zurückzuführen sind.
- Die Rede von einer "Erholung" des arktischen Meereises ist irreführend.
- Der negative Trend setzt sich nicht nur fort, sondern vielmehr ist eine Beschleunigung der Abnahme feststellbar.
- Die Ergebnisse der letzten IPCC-Modellrechnungen werden durch die Beobachtungen überholt. Der tatsächliche Rückgang findet wesentlich schneller statt, als in den Projektionen vorhergesagt wurde.
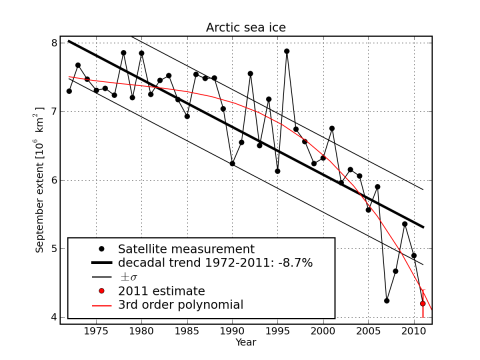
Abb. 2: September Meereis-Bedeckung in der Arktis (September-Mittelwerte) aus Satelliten-Daten. Der rote Punkt markiert eine statistische Schätzung für den September-Mittelwert samt Unsicherheit. (Daten aktualisiert nach Milke, A., G. Heygster 2009: Trend der Meereisausdehnung von 1972-2009. Technical Report, Institute of Environmental Physics, University of Bremen, August 2009, 41 pages.)
Abbildung 2 zeigt die September Meereis-Fläche über einen Zeitraum von 40 Jahren. Es zeigt sich, dass ein linearer Trend (schwarz) angesichts der Messwerte der letzten Jahre die Daten nicht mehr gut beschreibt. Ein sich beschleunigender Eisverlust (rote Linie) zeichnet sich ab. Eine verlässliche Prognose, wann erstmals mit einem weitgehend blauen arktischen Ozean zu rechnen ist, lässt sich daraus jedoch noch nicht ableiten.
 Lars Kaleschke ist Physiker und arbeitet als Juniorprofessor für Fernerkundung im Institut für Meereskunde am KlimaCampus der Universität Hamburg.
Lars Kaleschke ist Physiker und arbeitet als Juniorprofessor für Fernerkundung im Institut für Meereskunde am KlimaCampus der Universität Hamburg.
Links:
Mehr zur Abnahme der Eisdecke findet man in unseren früheren Beiträgen: Dirk Notz diskutierte den diesjährigen Juli-Rekord hier und die Schmelzsaison 2009 hier, Vergleiche mit Klimamodellen zeigten wir hier und hier, und die Frage "Kipp-Punkt oder nicht" diskutierten wir hier. Und in Zwei Planeten ging es um die bizarren Versuche der "Klimaskeptiker", den Eisschwund zu verleugnen ("das Eis weigert sich, wie befohlen zu schmelzen").
Derzeit ist auch die Polarstern am Nordpol unterwegs (mit KlimaLounge-Gastautorin Olivia Serdeczny an Bord) und macht Eisdickenmessungen.

Foto (c) S. Rahmstorf


Meereis Minimum
Zur Abschätzung der Entwicklung der Meereisfläche is die polynomische Näherung der Messwertpunkte ungeeignet. Diese liefert für größere Zeiten auf alle Fälle unendlich große Meereisflächen oder gar negative Eisbedeckungen. Zur Abschätzung der zeitlichen Entwicklung müssen andere mathematische Modelle herangezogen werden.
[Antwort: Die beiden Fits (linear und Polynom) sollen nur den vergangenen Verlauf illustrieren (d.h. die beobachtete Beschleunigung); sie stellen keine Prognosemethode dar. Stefan Rahmstorf]
Trend
In welchem Jahr trifft denn die rote Trendlinie auf die Abszisse?
@Werner Hasler
Die Fits sind natürlich keine Prognosemethode für größere Zeiträume. Aber wenn du z.B. den polynomalen Fit +/- 2 Standardabweichungen nimmst, dann kannst du einen Erwartungswert zumindest für die nächsten 1-2 Jahre ableiten. In so kurzen Zeiträumen ist nicht zu erwarten, dass sich der Trend so stark verändert, dass das ganze aus diesem Bereich herausfallen würde.
Für die Abschätzung der längerfristigen Eisentwicklung braucht man natürlich schon etwas komplexere Modelle, als einen einfachen statistischen Fit.
Außerdem denke ich, dass ein polynomaler Fit nicht unbedingt der geeignetste ist, um die Entwicklung des Meereises zu beschreiben. Andere Fits, z.B. Gompertz-Fits, sind hier IMO deutlich geeigneter, da sie nicht einfach immer weiter beschleunigt abfallen, sondern sich einen bestimmten Minimal-Wert annähern, genauso wie das das Meereis wohl auch tun wird.
Siehe z.B. hier:
http://neven1.typepad.com/…c-sea-ice-volume.html
statistische Ausreisser
Ich persönlich sehe 2007 schon als statistischen Ausreisser. Damals lagen aussergewöhnliche Wind- und Wetterverhältnisse vor, die zu dieser unerwartet starken Meereisschmelze geführt haben. In 2011 ist das anders. Aussergewöhnliche Wetterverhältnisse sind in diesem Jahr in der Arktis nicht zu beobachten. 2011 zeigt, dass das, was vor wenigen Jahren noch aussergewöhnlich war, nun gewöhnlich wird…
Mich erinnert das Jahr 2007 bei der arktischen Meereisschmelze an das Jahr 1998 bei den globalen Temperaturen. Die Temperaturen in 2010 haben gezeigt, dass 1998 kein einmaliger Ausreisser war…
Meereisdaten auf esa.int
Hier einige Artikel im Webauftritt der europäischen Raumfahrtbehörde esa, die unter anderem die Radarsatelliten Envisat und Cryosat betreibt:
http://www.esa.int/esaCP/SEMT7TRTJRG_index_0.html
http://www.esa.int/esaCP/SEMAAW0T1PG_index_0.html
http://earth.esa.int/…/area/index.cfm?fareaid=15
natürlicher Anteil
wenn sich nun die Arktis deutlich schneller erwärmt wie der Rest des Planeten (wie so oft…), dann muss man eben auch mal fragen, wie hoch der natürliche Anteil am Klimawandel sein mag und nicht pauschal immer so zu tun, als ob die Eisschmelze etc. praktisch nur auf unsere Emissionen zurück zu reduziert ist.
[Antwort: Die schnellere Erwärmung der Arktis hat zwei Hauptgründe:
1. “Polar amplification” – Klimaänderungen gleich welcher Ursache werden generell zum Nordpol hin verstärkt durch die Eis- und Schnee-Albedo-Rückkopplung.
2. Ruß. Die vom Menschen verursachten Rußemissionen schlagen sich auf Schnee und Eis nieder, machen sie dunkler und verringern damit auch die Albedo, es wird also mehr Sonnenwärme absorbiert.
Natürliche Anteile an der Erwärmung sind nicht bekannt – im Gegenteil, alle Studien kommen zu dem Schluss, dass aus natürlichen Gründen das Klima sich in den letzten Jahrzehnten abgekühlt hätte. V.a. die Sonne leuchtet in den letzten Jahren so schwach, wie seit Beginn der Satellitenmessungen in den 1970ern niemals.
Stefan Rahmstorf]
Herr Rahmstorf (G.I.oben)
die solare Aktivität ist erst seit ein paar Jahren relativ gering, kann als kaum messbare Klimawirkungen haben, wie sie selbst immer wieder korrekt festhalten. Wir hatten allerdings davor einige Dekaden mit relativ hoher solarer Leistung und diese haben zum Teil eben auch dazu beigetragen, dass mehr Eis um die Arktis geschmolzen ist und die bekannten positiven Feedbacks erzwungen hat und einen Zustand schufen, welcher höhere Temperaturen und weiteres Schmelzen verursacht. Das kann man nicht mit kurzfristigen Änderungen egal woher wegdenken. Rußpartikel mögen ihren kleinen Teil beitragen, sind aber sicher nicht entscheidend und so gesehen auch nicht mit dem anthropogenen Treibhauseffekt verknüfpt. Sie sehen gerne alles anthropogen, wie M. Mann mit seinem Hockeystick und sie wissen, dass sie damit dann doch zur Minderheit innerhlab der Klimawissenschaft gehören und sie wollen scheinbar gar nicht daran denken, dass sie nicht alles wissen. Das ist leider sehr offensichtlich.
sea-ice extent 2011 knapp hinter 2007
Vorerst mal Schmelzstopp (keine Abnahme des sea-ice extent) bei 4527000 km2 laut IARC-JAXA-Daten vom 10.9.11.
Recht viel weniger wird´s wohl nicht mehr werden.
Glaube nicht, daß das 2007er Minimum noch unterboten wird.
Die Eisdickenreduzierung ist schlimm genug.
Einige Anmerkungen zu den gezogenen Schlussfolgerungen im Artikel:
zu 1) Natürlich ist 2007 ein statistischer Ausreißer (genau so wie etwa 1996).
zu 2) u. 3) Von einer Erholung des Meereises auf Grund zweier Jahre (2008/2009) zu sprechen ist genau so falsch wie von einem beschleunigtem Schmelzen auf Grund zweier Jahre zu sprechen (2007/2011)!
zu4) Das ist ein Folgefehler von 3).
Die statistische Schätzung des Septembermittelwertes in der Grafik ist mathematisch unhaltbar:
http://www.ijis.iarc.uaf.edu/…a_Ice_Extent_L.png
Die Aussage, dass ein linearer Trend die Daten nicht mehr gut beschreibt, ist falsch. Diese Schlussfolgerung beruht einzig auf den Daten von 2011 (man stelle sich vor, 2011 wäre (wetterbedingt) eine Eisausdehnung wie 2009 eingetreten …).
Ansonsten aber ein guter Beitrag!
@U. Langer
Ich kann ihnen hinten und vorne nicht folgen.
Sie schreiben, dass die statistische Abschätzung oben mit dem polynomalen Fit mathematisch nicht haltbar sei. Die Abschätzung bezieht sich auf die Daten des NSIDC und beträgt 4,3 +/- 0,3 Mio km². Diese Schätzung trifft 100%ig zu, denn wir liegen gerade bei 4,4 Mio km² und damit exakt im Bereich der Schätzung.
Ihr verlinktes JAXA-Bild trägt zu ihrer Argumentation überhaupt nichts bei, weil sich die Schätzung wie gesagt auf die NSIDC Daten bezieht und die verwenden sowohl einen anderen Algorithmus als auch einen anderen Satelliten zur Messung und die Daten weichen daher von den JAXA-Daten ab. Den für die Schätzung relevanten aktuellen Sea-Ice Extent finden sie hier:
http://nsidc.org/…images/N_stddev_timeseries.png
Zweitens:
In der Grafik sieht man doch glasklar, dass der lineare Trend die Daten nicht mehr gut beschreibt. Berechnen sie doch mal das Residuum zwischen der Regressionsgerade und den Werten, und vergleichen das mal mit der polynomalen Regression. Die lineare Regression ist dabei um Welten schlechter und man sieht das ja auch schon mit bloßem Auge.
Ihre Kritik am Artikel ist daher völlig haltlos.
@ Beobachter
das 3. Polynom passt eben zufällig in die Reihe ganz gut rein, ist aber definitiv nur zur Veranschaulichung gut.
Stellen sie mal die gloable T Reihe mit diesem Polynom dar, sie werden am Ende eine Abkühlung sehen, was eben ein ziemlicher Blödsin ist, auch hier ist der lineare Fit viel besser geeignet.
Wie oben weiter einer richtig schreibt, nehmen sie doch das Jahr 2009 für 2011 und das 3. Polynom sieht ganz anders aus.
Wir sollten ja mittlerweile alle wissen, dass man einzelne Jahre nicht für Klimaaussagen verwenden kann.
@ Werner Hasler
Werner Hasler (08.09.2011, 16:42)
“… ist die polynomische Näherung der Messwertpunkte ungeeignet. Diese liefert für größere Zeiten auf alle Fälle unendlich große Meereisflächen oder gar negative Eisbedeckungen.”
Auch ein linearer Trend würde ungeändert negative Werte liefern – trotzdem kann der lineare oder polynomale Trend bis zum Punkt Null eine gute Näherung sein, denn erst ab Null werden die Voraussetzungen (Existenz von Eis) verlassen.
Soll ein solcher Punkt (Existenz von Eis) nicht gegeben sein, dann müßte man z.B. die Entwicklung des Wärmegehalts der oberen (50m?) angeben.
MfG
Haltlose Kritik
@Beobachter
Die Realität hat den Artikel nicht gelesen.
09,09,2011,4526875
09,10,2011,4527813
09,11,2011,4537188
09,12,2011,4542656
09,13,2011,4589844
von hier die Daten
Sehr geehrter Beobachter,
Sie beobachten falsch! Die Abschätzung im Artikel liegt bei 4,2 ± 0,2 Mill km². Damit liegen Ihre derzeitigen 4,4 Mill km² an der oberen Grenze. Wenn Sie jetzt noch ihren eigenen Link richtig beobachten, sollte auch Ihnen klar werden, dass diese Abschätzung Murks ist.
Zu Ihrem 2. hat ja schon Herr Innerhofer geantwortet, was ich nur noch mit dem Rat verbinden würde, sich bei solchen graphischen Darstellungen eben nicht nur auf das bloße Auge zu verlassen. Ich kann Ihnen auch problemlos eine andere Grafik erstellen, in denen der lineare Trend viel besser aussieht als die obige polynomale Regression – z.B. wenn ich im Gegensatz zum obigen Artikel nicht auch die groben Schätzwerte der 70iger Jahre verwende sondern mich allein auf die genaueren Satellitenbeobachtungen seit 1979 stütze.
MfG
@Gunnar Innerhofer
Auch das was du hier schreibst ist (wie fast immmer) schlicht falsch.
> Stellen sie mal die gloable T Reihe mit
> diesem Polynom dar, sie werden am Ende
> eine Abkühlung sehen, was eben ein
> ziemlicher Blödsin ist, auch hier ist
> der lineare Fit viel besser geeignet.
Ziemlicher Blödsinn ist nur ihre falsche Behauptung. Dass dies nicht stimmt, sieht man einfach, in dem man es schlicht ausprobiert:
http://imageshack.us/…stempannualglobalmean.png/
Weder ist der linear Fit hier besser (ist er nicht) noch geht der polynomiale Fit am Ende ins Negative.
> Wie oben weiter einer richtig schreibt,
> nehmen sie doch das Jahr 2009 für 2011
> und das 3. Polynom sieht ganz anders
> aus.
Auch das ist schlicht Unsinn. Erstens ist 2011 überhaupt nicht zur Berechnung des Fits verwendet in obiger Grafik, weil die Daten hier noch gar nicht vorliegen (der Sinn der Grafik war es ja, den Wert für 2011 aus dem Fit der Jahre 1979-2010 abzuschätzen). Es sind also nur die Jahre bis 2010 berücksichtigt. Aber egal, selbst wenn man den vorläufigen Wert für 2011 und 2010 weglässt (derzeitiger September-Durchschnitt 4,4 Mio km²) oder nur 2010, der Fit schaut in keinster Weise “ganz anders” aus, sondern fast identisch. Auch diese Behauptung von ihnen kann man leicht widerlegen, indem man es einfach mal ausprobiert:
http://imageshack.us/…nsidcsepsiepolynomial.png/
Der Fit für 1979-2010 ist optisch von dem Fit für 1979-2011 nicht mal zu trennen und selbst der Fit für 1979-2009 ist bis auf einen winzigen Unterschied gleich. Der Fit für 1979-2009 ist sogar zum Ende hin steiler, durch die neuen Daten ist er also sogar einen kleinen Tick flacher geworden, und nicht wie sie vermutlich denken steiler.
Und auch mit dem linearen Fit kann man dieses Spielchen machen und auch dieser weicht natürlich mit den Daten bis 2009 nicht nennenswert ab:
http://imageshack.us/f/593/nsidcsepsielinear.png/
> Wir sollten ja mittlerweile alle
> wissen, dass man einzelne Jahre nicht
> für Klimaaussagen verwenden kann.
Genau. Und ein Fit über 30 Jahre ist ein Fit über 30 Jahre und nicht das Heranziehen einzelner Jahre. Deshalb verändert sich der Fit ja auch durch Hinzunahme von 1-2 Jahren ja auch nicht. DAS ist ja gerade der Sinn von solchen Regressionen, dass man STABILE Trends bekommt und eben kein Jahr-zu-Jahr-Rauschen.
Angesichts dessen, dass alle deine Aussagen hier völlig falsch waren, würde ich dir raten, dich entweder mal richtig in die Statistische Mathematik einzuarbeiten oder in Zukunft vielleicht einfach mal nix sagen, wenn man keine Ahnung hat?
@ Beobachter
Naja,
ich hatte das mal mit den Hadley Daten angestellt und die 30a Reihe zeigt mit dem 3. Polynom dann folgendes Bild:
http://i52.tinypic.com/2r5tjf4.png
Sie sehen also, dass man damit fast alles zeigen kann, was man gerade will und mit Polynomen egal welchen Grades arbeitet normal niemand in der Klimaforschung.
@U. Langer
> Die Abschätzung im Artikel liegt bei 4,2
> ± 0,2 Mill km². Damit liegen Ihre
> derzeitigen 4,4 Mill km² an der oberen
> Grenze. Wenn Sie jetzt noch ihren eigenen
> Link richtig beobachten, sollte auch
> Ihnen klar werden, dass diese Abschätzung
> Murks ist.
Das erklären sie mir jetzt mal. Selbst wenn die Ausdehnung nach NSIDC-Daten am Ende des Monats bei 4,4 Mio km² liegt, dann liegt sie trotzdem noch immer im Bereich der Schätzung. Und selbst wenn sie am Ende bei 4,5 Mio km² liegen sollte, und damit um nur 0,1 Mio km² außerhalb des Schätzbereichs, dann ist das immer noch bei weitem besser, als die 5,4 Mio km² die man an der linearen Regression ablesen kann. Eine Abschätzung die nur um 0,3 Mio km² daneben liegt, ist nicht “Murks” sondern ziemlich genau (mehr als 3x so genau wie die Abschätzung anhand der linearen Regression).
Und was die Zahlen von Aladin angeht: Das sind wieder die JAXA-Daten – nicht die NSIDC Daten auf die sich die diskutierte Grafik im Artikel bezieht. Ihr könnte jetzt noch so oft die Zahlen vermischen, wenn es euch gerade in den Kram passt, aber glaubwürdig wird eure Argumentation damit nicht. Genauso hast du noch immer nicht ein einziges Argument gebracht, wieso die lineare Regression besser zu den Daten passt, als die polynomiale Regression.
Ganz im Gegenteil: Dass du dich vor einem vernünftigen Beleg drückst, z.B. einem Vergleich der Residuuen beider Regressionen, zeigt mir nur allzu deutlich, dass dir die Argumente zur Stützung deiner Behauptung längst ausgegangen sind.