Erster Erd-Trojaner entdeckt (Oder ist es ein Erd-Grieche?)
BLOG: Go for Launch

Die Himmelsmechanik in einem Planetensystem kann ziemlich kompliziert sein. Auch wenn man nur die Sonne und einen Planeten betrachtet, überlagern sich die Schwerefelder beider zu einem Potenzial, in dem es “Gleichgewichtspunkte” gibt.
Gleichgewichtspunkte sind nicht etwa Punkte, in denen sich die Summe aller Schwerkräfte zu Null addiert. Es handelt sich einfach um Punkte, in denen besondere Verhältnisse herrschen, die sich aber zwischen den einzelnen Punkten deutlich unterscheiden.
Die Lagrangepunkte L1 und L2
Die Gleichgewichtspunkte (auch bekannt als Librationspunkte oder Lagrange-Punkte) L1 und L2 findet man auf der gedachten Linie, die die Sonne mit dem betreffenden Planeten verbindet. L1 ist zwischen Planet und Sonne, L2 von der Sonne aus gesehen jenseits des Planeten. Wie weit diese Punkte vom Planeten entfernt sind, hängt von der Masse des Planeten ab und von seiner Entfernung von der Sonne. Im Fall der Erde beträgt der Abstand rund 1.5 Millionen km.
Das besondere an L1 und L2 ist, dass es sich um instabile Gleichgewichtspunkte handelt. Ein Objekt kann in oder nahe einem dieser Punkte eine Umlaufperiode um die Sonne erzielen, die nicht der Periode entspricht, die sich eigentlich aus seinem Sonnenabstand ergeben würde, sondern genau bei einem Erdjahr liegt. Diesen Umstand macht man sich technisch zunutze, um beispielsweise orbitale Teleskope wie Herschel und Planck in weiten Schleifen um einen Lagrangepunkt fliegen und von dort aus ihre Beobachtungen durchführen zu lassen.
L1 und L2 sind instabile Punkte. Wenn die Bahn des Objekts nicht konstant nachgeregelt wird, werden selbst kleinste Störungen dazu führen, dass das Objekt die Region um den Lagrangepunkt permanent verlässt. Ohne in Details zu gehen: dank dieser Instabilität kann ein Objekt aus einer weiten, elliptischen, und damit noch an den Planeten gebunden Bahn ohne äußere Zufuhr von Energie das Schwerefeld des Planeten verlassen und stattdessen in eine Bahn um die Sonne eintreten. Umgekehrt kann es auch zu einem rein gravitativen Einfang kommen.
Die Lagrangepunkte L4 und L5
Ganz anders sind die Lagrange-Punkte L4 und L5. Diese befinden sich auf der Planetenbahn, L4 60 Grad voreilend und L5 60 Grad nacheilend. Also spannen Planet, Sonne und Lagrangepunkt L4 oder L5 gleichseitige Dreiecke auf. Deswegen ist der Abstand von der Erde zum Lagrangepunkt L4 oder L5 im Erde-Sonne-System auch eine astronomische Einheit – 149.6 Millionen km. Bei einem gleichseitigen Dreieck sind nämlich alle Seiten gleich lang.
 L4 und L5 sind stabile Gleichgewichtspunkte. Wenn man ein Objekt in der Nähe eines dieser Punkte positioniert, mit einer Geschwindigkeit, die nahe an der Bahngeschwindigkeit der Erde liegt und einer Richtung, die in etwa der Flugrichtung der Erde entspricht, die sie an diesem Punkt auf ihrer Bahn hätte, dann wird das Objekt zwar nicht genau in dem Lagrange-Punkt bleiben. Selbst wenn Position und Geschwindigkeit ganz haargenau “richtig” wären, gäbe es ja immer noch Bahnstörungen durch die Anziehungskraft anderer Planeten oder durch nicht-gravitative Effekte.
L4 und L5 sind stabile Gleichgewichtspunkte. Wenn man ein Objekt in der Nähe eines dieser Punkte positioniert, mit einer Geschwindigkeit, die nahe an der Bahngeschwindigkeit der Erde liegt und einer Richtung, die in etwa der Flugrichtung der Erde entspricht, die sie an diesem Punkt auf ihrer Bahn hätte, dann wird das Objekt zwar nicht genau in dem Lagrange-Punkt bleiben. Selbst wenn Position und Geschwindigkeit ganz haargenau “richtig” wären, gäbe es ja immer noch Bahnstörungen durch die Anziehungskraft anderer Planeten oder durch nicht-gravitative Effekte.
Trojaner
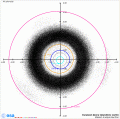
Die Bahnen von Objekten, die um L4 oder L5 gefangen sind, können sogar ganz erheblich vom theoretischen Gleichgewichtspunkt abweichen. Die nebenstehende Grafik zeigt die Positionen aller zu einem Referenzzeitpunkt bekannten Asteroiden im Sonnensystem zusammen mit den Planeten bis hinaus zum Jupiter. Man sieht, wenn man Jupiter betrachtet, zweierlei:
- Es gibt eine beträchtliche Anzahl von Objekten nahe der Jupiterbahn, die sich voreilend oder nacheilend in umschriebenen Regionen nahe der Jupiterbahn gruppieren. Dies sind die Jupiter-Trojaner. Der erste wurde 1906 entdeckt; mittlerweile sind über 4000 bekannt, und zwar etwa doppelt so viele um L4 wie um L5, warum auch immer.
- Die Position der einzelnen Trojaner weicht erheblich von der Idealposition ab. Dies gilt auch in der hier nicht gezeigten Dimension außerhalb der Ekliptikebene. Die Bahnen von Trojanern können erheblich geneigt sein.
Trotz dieser großen Abweichungen bleibt die Gruppierung klar erkennbar. Der Schwerkrafteinfluss des Planeten führt die Objekte in die Regionen um die zwei Lagrangepunkte zurück. Allerdings funktioniert dies nicht unbeschränkt. Mit der Zeit werden einzelne Objekte die Region verlassen, in der sie gefangen waren. Dafür können neue eingefangen werden.
Auch gibt es eine Grauzone zwischen Trojanern und solchen Objekten, die sich einfach nur in einer erdähnlichen Bahn befinden, die aber periodisch dem Planeten sehr nahe kommen kann. Da redet man von Hufeisenbahnen (engl.: “horseshoe orbits”). Im Fall der Erde liegt die Periode zwischen nahen Begegnung bei rund 30 Jahren. Bei einer solchen Begegnung kann die scheinbare Bahnevolution sich umkehren, oder das Objekt kann temporär von der Erde eingefangen werden oder mit Erde oder Mond kollidieren.
Die Unterscheidung zwischen einem echten Trojaner, der sich immer noch weit von dem “stabilen” Lagrangepunkten entfernen kann, in dessen Region er gefangen ist und einem Objekt in einer Hufeisenbahn bedarf der Beobachtung über einen langen Zeitraum hinweg und der genauen Bahnbestimmung.
 Es sind viele mit der Erde ko-orbitale Objekte in Hufeisenbahnen bekannt, aber es konnte noch kein Erd-Trojaner nachgewiesen werden. Bis jetzt: denn nun gelang es offenbar mittels Beobachtungen des Weltraumteleskops WISE und dem Canada-France-Hawaii-Teleskop auf dem Vulkan Mauna Kea nachzuweisen, dass der Asteroid 2010 TK7 ein Erd-Trojaner ist. WISE – Wide-field Infrared Survey Explorer – ist ein orbitales Infrarot-Teleskop, dessen Mission eine Phase namens NEOWISE umfasste. Diese ist seit Januar 2011 abgeschlossen und gestattete die Beobachtung von mehr als 150,000 Asteroiden.
Es sind viele mit der Erde ko-orbitale Objekte in Hufeisenbahnen bekannt, aber es konnte noch kein Erd-Trojaner nachgewiesen werden. Bis jetzt: denn nun gelang es offenbar mittels Beobachtungen des Weltraumteleskops WISE und dem Canada-France-Hawaii-Teleskop auf dem Vulkan Mauna Kea nachzuweisen, dass der Asteroid 2010 TK7 ein Erd-Trojaner ist. WISE – Wide-field Infrared Survey Explorer – ist ein orbitales Infrarot-Teleskop, dessen Mission eine Phase namens NEOWISE umfasste. Diese ist seit Januar 2011 abgeschlossen und gestattete die Beobachtung von mehr als 150,000 Asteroiden.
 Es handelt sich bei 2010 TK7 um einen etwa 300 Meter großen Asteroiden in einer Bahn, die um mehr als 20 Grad gegenüber der Erdbahn geneigt ist. Auch der bahnradius weicht wegen ihrer Exzentrizität stark von einer astronomischen Einheit ab. Gerade der Exzentrizität der Bahn ist die Identifizierung als Erd-Trojaner zu verdanken, denn diese erleichterte die Beobachtbarkeit während der NEOWISE-Missionsphase. Der Asteroid wird sich jedoch in den nächsten 100 Jahren, für die die Bahn numerisch vorausberechnet wurde, der Erde nicht auf mehr als 24 Millionen km nähern. Es ist wohl damit zu rechnen, dass noch weitere Objekte als Erdtrojaner identifiziert werden.
Es handelt sich bei 2010 TK7 um einen etwa 300 Meter großen Asteroiden in einer Bahn, die um mehr als 20 Grad gegenüber der Erdbahn geneigt ist. Auch der bahnradius weicht wegen ihrer Exzentrizität stark von einer astronomischen Einheit ab. Gerade der Exzentrizität der Bahn ist die Identifizierung als Erd-Trojaner zu verdanken, denn diese erleichterte die Beobachtbarkeit während der NEOWISE-Missionsphase. Der Asteroid wird sich jedoch in den nächsten 100 Jahren, für die die Bahn numerisch vorausberechnet wurde, der Erde nicht auf mehr als 24 Millionen km nähern. Es ist wohl damit zu rechnen, dass noch weitere Objekte als Erdtrojaner identifiziert werden.
Weitere Information
Pressemitteilung “NASA’s WISE Finds Earth’s First Trojan Asteroid” vom 27. Juli 2011, Quelle: NASA/JPL
WISE-Missionswebseite, Quelle: NASA/JPL


Trojaner
Ich möchte noch eine kleine Erklärung zur Abrundung dieses schönen Beitrags einfügen. Ich habe mich nämlich gefragt wie es zu dem Begriff Trojaner gekommen ist.
Wikipedia: “Die bislang gefundenen Trojaner sind nach den Personen aus Homers Ilias benannt: die vorauseilenden Asteroiden nach den griechischen (bis auf Hektor), die nacheilenden nach den trojanischen Helden.”
[Antwort: Vielen Dank für den Hinweis! Das ist allerdings eine gute Frage. Ich nehme an, den Ausschlag für die Namenskonvention gab die Tatsache, dass der erste entdecke Trojaner “Achilles” getauft wurde, wobei dessen Entdecker noch nicht gewusst haben konnte, dass sich ihm hinterher noch eine ganze Heerschar hinzugesellen würde. MK]
noch was gefunden
Sogar zwischen Griechen und Trojanern wird unterschieden. Grün sind die “Griechen” und “Trojaner” des Jupiter. Genau genommen müsste man also davon sprechen, dass man einen Griechen gefunden hat, denn auf L4 gibt es nun mal keine Trojaner.
http://upload.wikimedia.org/…rSolarSystem-en.png
Ich habe die Meldung vom neu entdeckten Griechen 🙂 gestern gelesen und habe das heute Nacht zum Anlass genommen mich mal mit Lagrange und den Lagrangepunkten zu befassen. Da liest man dann so nette Sachen wie von der “Gegenerde” auf L3. Warum wo welche Instrumente geparkt werden, etc. versteht man eigentlich nur wenn man diese Physik begriffen hat.
Frage: Wird eigentlich die Rückseite der Sonne von L3 aus beobachtet?
[Antwort zum L3-Punkt: Ja, Sie haben Recht, den hatte ich in meinem Text gar nicht erwähnt. Er würde sich zwar zur Beobachtung der Sonnenrückseite eignen, aber man würde die Daten nicht zur Erde funken können; die Sonne wäre im Weg. Das wäre so etwas wie eine permanente obere Konjunktion.
Es ist allerdings auch gar nicht notwendig, eine Sonde genau dort zu positionieren. Erstens kann man allein schon durch Beobachtung der Sonnenvorderseite darauf schließen, was auf der Rückseite vor sich geht, siehe dieser BBC-Artikel. Zweitens gibt es die NASA-Mission STEREO, bei der jeweils ein Sonnenteleskop vor- und eins nacheilend von der Erde wegdriftet und so auch die gerade erdabgewandte Seite “gesehen” werden kann.
Einen Film zum L3-Punkt gibt es natürlich auch. MK]
Griechen und Trojaner
Kleine Anmerkung hierzu:
“[…] denn auf L4 gibt es nun mal keine Trojaner.”
Doch, Hektor ist ein einsamer Trojaner im griechischen Lager L4. Dafür haben die Griechen mit Patroklos einen Spion bei den Trojanern in L5. Was die griechischen Heroen aber davon halten würden, dass sie kurzerhand als “Trojaner” in den Himmel befördert wurden?
—
L3 ist ein instabiles Equilibrium, schon daher als permanenter Beobachtungsposten wohl uninteressant.
[Antwort zum Thema der Instabilität von L3: Es ist zwar richtig, dass L3 formal ein instabiler Gleichgewichtspunkt ist, allerdings dürfte das Gleichgewicht dort fast schon indifferent sein. Wenn man sich die Instabilität von L1 und L2 als die einer Kugel auf dem gerundeten Gipfel eines Zuckerhuts vorstellt, dann wäre die Instabilität von L3 in etwa die auf dem Gipfel eines sehr flachen Berges, fast schon einer Ebene.
Instabilität allein ist auch kein Grund, warum eine Lokation uninteressant für Raumsonden sein sollte. Schließlich steht die Instabilität von L2 auch nicht der Tatsache entgegen, dass man dort (bzw. in Lissajous-Kurven um den Punkt) Observatorien positioniert.
Der Betrieb einer Sonde nahe am L3-Punkt wäre bahnmechanisch kein Problem. Das Problem ist wirklich die Kommunikation trotz der Störungen durch die immer in der Sichtlinie stehende Sonne. MK]
“Was die griechischen Heroen aber davon halten würden, dass sie kurzerhand als “Trojaner” in den Himmel befördert wurden?”
Schlimmer ist doch, dass sich die Trojaner heutzutage als Computerviren beschimpfen lassen müssen, dabei waren das doch die fiesen Griechen mit ihrem Holzpferd! Sowas von ungerecht!
@Jan Hattenbach
Stimmt. Das Leben ist halt ungerecht — im Himmel wie auf Erden.
@all: Griechen vs. Trojaner
OK, Leute, ich habe den Titel geändert. Ich hoffe, damit sind alle Beteiligten, auch die aus der Antike, zufrieden!
@Michael Khan
L1, L2, und L3 sind eigentlich Sattelpunkte des Gravitationspotentials. Man muss jedenfalls korrigieren, um nicht durch Störungen da hinausgekegelt zu werden. Aber es existieren geeignete Orbits um diese Punkte, auf denen man mit vergleichsweise geringem Aufwand in deren Nähe verbleiben kann, und das wird offenbar auch praktiziert. Sind also doch keine so prinzipiell ungeeigneten Positionen zur Observation, wie es zunächst den Anschein haben mag.
[Antwort: Nicht ich, sondern Sie haben weiter oben behauptet, die Instabilität stünde der Nutzung entgegen. Dass es Lösungen des restringierten Dreiköperproblems gibt, die zu Bahnen führen, die die Form von Lissajous-Kurven haben, habe ich ebenfalls bereits geschrieben. Mehr zu den instabilen Lagrangepunkten L1 und L2 und ihrer Nutzung hier. MK]
Sattelfläche
Die Instabilität von L1 und L2 ist die einer Kugel auf einer Sattelfläche.
Ein massearmes Objekt wird zur Verbindungslinie der beiden massereichen Objekte hin gezogen, und nicht von ihr weg.
Bei kleinen Abweichungen von L1 und L2 wird das massearme Objekt aber zu einem der beiden massereichen Objekte hin gezogen.
Übrigens, Halo 1 schwebte am L1-Punkt zwischen dem Gasriesen Threshold und seinem Mond Basis.
[Antwort: Die Darstellung mit dem Sattelpunkt ist richtig, aber mir ging es in dem von mir bemühten Vergleich eigentlich nur um die Illustration des Begriffs “instabiles Gleichgewicht”, ohne dabei auch noch auf die spezielle Situation der Hill-Flächen eingehen zu wollen.
Kein Objekt kann jemals direkt in einem Lagrange-Punkt positioniert werden. Man wählt immer Lissajous-Kurven um den theoretischen Gleichgewichtspunkt herum. Diese Kurven repräsentieren Äquipotenzialzonen, von denen andere solche Zonen (stabile und instabile Mannigfaltigkeiten) verzweigen, die einen hinunter in Planetennähe, die anderen fort vom Planeten. Wenn ein Objekt in einer Lissajous-Lurve nicht mehr gesteuert wird, dann wird es über kurz oder lang in eine solche Mannigfaltigkeit eintreten und kann so entweder in einer hochexzentrischen bahn um den Planeten oder in einer heliozentrischen Bahn landen. MK]
@Michael Khan
“Nicht ich, sondern Sie haben weiter oben behauptet, die Instabilität stünde der Nutzung entgegen. Dass es Lösungen des restringierten Dreiköperproblems gibt, die zu Bahnen führen, die die Form von Lissajous-Kurven haben, habe ich ebenfalls bereits geschrieben.“
Ist ja gut, habe ich inzwischen doch eingesehen.
N.B. L1, L2, und L3 wurden übrigens von Euler enteckt (ca. 1750), L4 und L5 gehen auf das Konto von Lagrange (ca. 1760). Die Publikationen erschienen in beiden Fällen aber erst einige Jahre später (Euler 1767, Lagrange 1772).
@Michael
schöne idee mit dem rot und so
[Antwort: Leider ist das LifeType-System, auf dem diese Blogs aufsetzen, mit einigen Schwächen behaftet. Eine davon ist, dass man Antworten auf Kommentare nicht direkt unter die betreffenden Kommentare platzieren kann, sie erscheinen in der Liste erst viel weiter unten, weil sie in chronologischer Reihenfolge gelistet werden.
Da wird es, wenn die Diskussion länger wird (was hier allerdings noch nicht der Fall ist) sehr schwierig, mitzuverfolgen, wer wann was gesagt hat und wer was darauf geantwortet hat. Das zwingt die Blogger zu etwas Kreativität. Meine Lösung ist sicher auch nicht der Weisheit letzter Schluss, aber ich hoffe, sie macht die Diskussionen ein klein wenig übersichtlicher. MK]